МОДЕЛИРОВАНИЕ ОСТАТОЧНЫХ ДЕФОРМАЦИЙ, НАКАПЛИВАЕМЫХ ЩЕБЕНОЧНЫМИ МАТЕРИАЛАМИ В ПОКРЫТИЯХ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ДОРОГ
Александров А.С.
ORCID: 0000-0003-2009-5361, Кандидат технических наук, Сибирская государственная автомобильно-дорожная академия
МОДЕЛИРОВАНИЕ ОСТАТОЧНЫХ ДЕФОРМАЦИЙ, НАКАПЛИВАЕМЫХ ЩЕБЕНОЧНЫМИ МАТЕРИАЛАМИ В ПОКРЫТИЯХ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ДОРОГ
Аннотация
Применением интегральных уравнений наследственных теорий получены формулы, позволяющие вычислять необратимые деформации, накапливаемые щебеночными материалами, используемыми в конструктивных слоях покрытий и оснований дорожных одежд сельскохозяйственных автомобильных дорог. Этот подход позволил получить логарифмические модели с одним и двумя параметрами материала, а также степенные модели, включающие в себя два или три параметра материала. Для определения параметров материала степенных и логарифмических моделей анализируются данные трехосных испытаний щебеночных материалов, выполненные в динамических приборах трехосного сжатия, позволяющих исследовать процесс накапливания остаточной деформации в условиях воздействия повторных нагрузок.
Ключевые слова: сельскохозяйственная дорога, остаточная деформация, трехосное сжатие.
Aleksandrov A.S.
ORCID: 0000-0003-2009-5361, PhD in Engineering, Siberian State Automobile and Highway Academy
MODELING PERMANENT DEFORMATION ACCUMULATES IN THE COATED MACADAM MATERIALS FARM ROADS
Abstract
Application of integral equations of the theory of heredity derive formulas allowing to calculate the irreversible deformation accumulated crushed stone materials used in structural layers of coatings and bases of road clothes of farm roads. This approach yielded logarithmic model with one or two parameters of the material and the degree of the model, including two or three parameters of the material. To determine the parameters of the material power and logarithmic models analyzes data triaxial crush materials made in dynamic devices triaxial, allowing to explore the process of accumulation of permanent deformation under the effect of repeated loads
Keywords: farm road, permanent deformation, triaxial compression.
Потребительские свойства автомобильной дороги зависят от ровности покрытий, что обуславливает актуальность работ, направленных на прогнозирование изменения ровности покрытий. Глубина неровности в рассматриваемой точке определяется разностью необратимых перемещений поверхности покрытия в этой точке и в точке с наименьшим остаточным смещением [1, С. 46]. Например, глубина колее в точке, расположенной в пределах полосы наката, определяется разностью остаточных смещений покрытия в этой точке и в точке, расположенной за пределами полосы наката, в которой величина остаточного перемещения поверхности покрытия минимальна. Так как максимальная величина остаточной деформации накапливается в центре полосы наката, то критерий расчета дорожной одежды по ограничению глубины колеи можно записать в виде [1, С. 46]:
![]() (1)
(1)
где Sпmax – максимальная величина необратимого перемещения поверхности покрытия в сечении расположенном в центре полосы наката, в котором имеет место максимальное число проездов транспортных нагрузок, мм; Sпmin – минимальная величина необратимого перемещения поверхности покрытия в сечении расположенном за пределами полосы наката, в котором имеет место наименьшее число проездов транспортных нагрузок, мм; hпр – предельная глубина колеи, ограничиваемая нормативными документами.
Величину остаточного перемещения поверхности покрытия можно определить суммой необратимых смещений, испытываемых конструктивными слоями и земляным полотном. В сечении по оси симметрии нагрузки остаточное перемещение любого i-го конструктивного слоя и земляного полотна вычисляется интегрированием функции необратимой деформации по глубине зоны ее распространения [2, С. 70-72]. Такое решение задачи сводится к интегральному уравнению:
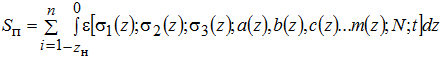 (2)
(2)
где zн – расстояние от точки, расположенной на поверхности слоя в сечении по оси симметрии нагрузки до точки, ограничивающей зону распространения необратимых деформаций, расположенной в этом же сечении, мм; σ1(z), σ2(z), σ3(z) – максимальное и минимальные главные напряжения (в сечении по оси симметрии нагрузки σ2=σ3, а σ1>σ2 и σ1>σ3), Па; a(z), b(z), c(z)…m(z) – параметры материалы, представляющие собой функцию физических параметров материала, изменяющихся по глубине; N – число повторных нагрузок в рассматриваемом сечении; t – время воздействия одной нагрузки, с.
Таким образом, определение подынтегральной функции уравнения (2) является важной задачей прогнозирования изменения ровности дорожной конструкции.
Математическое моделирование пластической деформации в условиях трехосного сжатия дискретных материалов и воздействия повторных (циклических) нагрузок является целью работ, выполняемых во всем мире. Особенностью таких моделей является представление, накапливаемой пластической деформации εN, произведением функции числа нагрузок f(N) и деформации εn, накапливаемой от сравнительно малого числа повторных нагрузок n (n<<N). То есть
![]() (3)
(3)
При подборе эмпирических формул (3) количество нагрузок принимают в пределах n=1…103, а N=105…106 и более. Испытания образцов из грунтов и щебеночных материалов выполняют при помощи динамических приборов трехосного сжатия [3, С. 27].
В настоящее время получены логарифмические, степенные и экспоненциальные функции количества нагрузок, используемые в моделях типа (3). Предложение использовать логарифмические зависимостей для прогнозирования величины пластической деформации принадлежит Р.Д. Барксдейлу [4, С. 164]. Г. Свери в своей диссертации [5, С. 54] предложил использовать степенные функции, которые получили развитие в работах [6, C. 278], [7, С. 45]. Экспоненциальные зависимости использованы в работах [8, С. 252], [9, С. 1138].
Точность этих зависимостей обуславливается числом нагрузок N, от воздействия которых выполняется прогнозирования накапливаемой деформации eN. При сравнительно малом числе приложенных нагрузок N≤103 наилучшее приближение дают экспоненциальные функции. При числе нагрузок, варьирующемся в диапазоне 103>N≤105, наибольшей точностью обладают логарифмические зависимости. Степенные зависимости позволяют с наибольшей точностью прогнозировать пластические при числе нагрузок 105>N≤3×106, вследствие чего наиболее пригодны для расчетов деформаций материалов дорожных конструкций. Кроме того, степенные функции позволяют получать результаты с приемлемой точностью и для меньшего числа нагрузок.
Вследствие зависимости точности расчета пластических деформаций от числа повторных нагрузок для каждого типа функций можно указать область применения. Например, логарифмические функции могут быть использованы для расчета пластических деформаций материалов и грунтов, применяемых в дорожных конструкциях, на дорогах IV или V технических категорий. Степенные функции нужно применять при прогнозе деформаций материалов и грунтов для дорог I–III технических категорий. Экспоненциальные функции для наших целей не применимы.
Выполненный обзор показывает, что математическое моделирование пластического деформирования материалов и грунтов выполняется подбором эмпирических формул. Обилие эмпирических формул и отсутствие теоретического обоснования приводит к затруднениям при выборе математической модели. В силу того, что такая формула является подынтегральной функцией уравнения (1), то решение задачи о пластическом смещении поверхности покрытия, а значит и глубине неровности так же затруднено.
Поэтому автор поставит задачу поиска теоретического решения, которое позволит получить обобщающую математическую модель для ряда известных эмпирических формул.
Анализ данных лабораторных трехосных динамических испытаний позволяет сделать вывод, что величина наблюдаемой пластической деформации, приобретаемой образцом при реализации N-ой по счету нагрузки, зависит как от этой, так и от всех предшествующих нагрузок. Следовательно, пластическое деформирование материалов и грунтов при приложении повторных нагрузок имеет наследственный характер. Поэтому для математического моделирования таких пластических деформаций можно воспользоваться интегральными уравнениями теории ползучести, в которых функция времени должна быть заменена функцией числа нагрузок.
Анализируя деформирование материалов и грунтов, отметим, что в процессе каждого приложения нагрузки пластическая деформация увеличивается во времени, то есть непрерывно возрастает от начала к концу воздействия рассматриваемой нагрузки. Таким образом, процесс накапливания пластических деформаций можно считать непрерывным, а для их расчета можно выполнить интегрирование по числу нагрузок. Подынтегральные выражения примем в виде степенных функций, определяющих приращение пластической деформации от нагрузки с порядковым номером n. Тогда ядра интегральных уравнений дадим в виде:
![]() (4)
(4)
![]() (5)
(5)
где Δεмп и Δεвп – соответственно мгновенная и вязкопластическая деформации возникающие от нагрузки с порядковым номером п; a, b и c – параметры модели, учитывающие вид материала и величину напряжений.
Тогда интегральные уравнения дадим в виде:
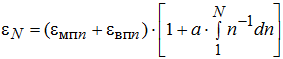 (6)
(6)
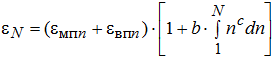 (7)
(7)
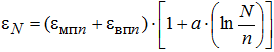 (8)
(8)
где εмпn и εвпn – мгновенная и вязкая составляющие пластической деформации, накапливаемой при воздействии n-го числа нагрузок (n<<N); a – параметр логарифмической модели, учитывающий величину напряжений, вид материала и показатели его физических свойств (платность, влажность и т.п.).
Взяв интеграл от (7), имеем
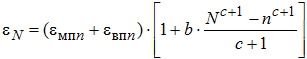 (9)
(9)
где b и c – параметры степенной модели, учитывающие те же факторы, что и параметр a в модели (8).
Если число нагрузок n сравнительно мало и составляет n=10; n=100 или n=200, то связь составляющих eмпn и eвпn пластической деформации с этим числом нагрузок и остаточными деформациями от первого воздействия нагрузки целесообразно искать в виде
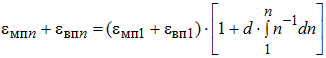 (10)
(10)
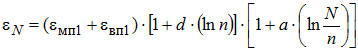 (12)
(12)
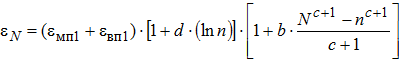 (13)
(13)
Область применения моделей (12) и (13), а так же их параметры a, b, c и d необходимо устанавливать на основе анализа экспериментальных данных по трехосному сжатию материалов и грунтов циклической нагрузкой. При этом из всего многообразия опытных данных для решаемой задачи пригодны только те, которые получены при достаточно большом числе приложений нагрузки N>105 . Такие эксперименты выполняются за рубежом при помощи динамических приборов трехосного сжатия. Конструкции приборов трехосного сжатия и методы экспериментальных испытаний отличаются многообразием. Поэтому анализ таких приборов и экспериментальных методов заслуживает рассмотрения в отдельной статье. В настоящей публикации автор ограничится данными С. Веркмейстер [10], представленными на рис. 1 и рис. 2.
Анализируя данные рис. 1 и рис. 2, а так же подобные им зависимости, автор определил коэффициенты моделей (12) и (13). Здесь оговорим, что экспериментальные данные о пластическом деформировании материалов при воздействии циклических нагрузок получены другими специалистами, а значения коэффициентов a, b, c и d установлены автором по данным этих испытаний. Поэтому представленные ниже таблицы с коэффициентами a, b, c и d являются новыми, но вычисленными из известных экспериментальных данных.
В табл. 1 приведены значения коэффициентов n, a и d модели (12) для расчета деформации, накапливаемой щебеночным материалом из гранита или гнейса.
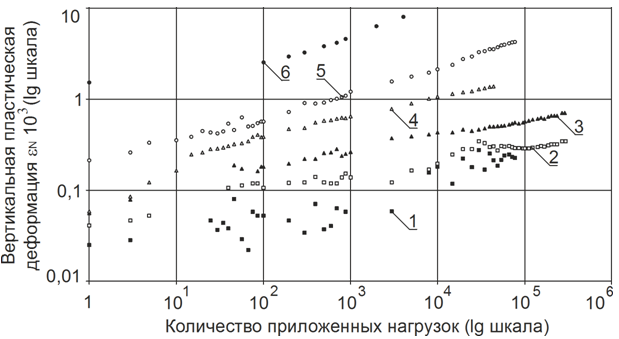
Рис. 1 - Зависимость вертикальной пластической деформации ГЩ от числа нагрузок и напряжений при s3=40 кПа по данным [10], 1 - 6 - при (σ1-σ3) 40; 80; 120; 160; 200 и 360 кПа; при s3=40 кПа
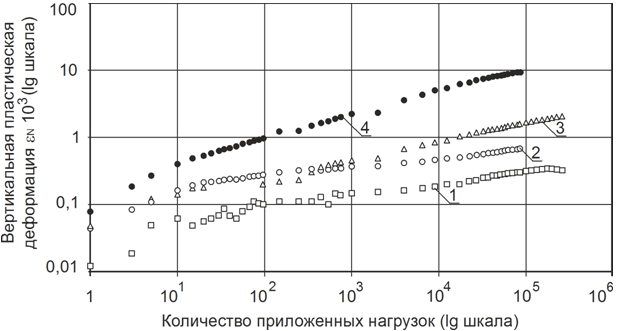
Рис. 2 - Зависимость вертикальной пластической деформации ПГС от числа нагрузок и напряжений при s3=40 кПа [10], 1 - 4 - при (s1-s3) 40; 80; 120; и 160 кПа; при s3=40 кПа
Таблица 1 - Параметры модели (12) для расчета остаточной деформации, накапливаемой образцом из гранитного или гнейсового щебня
| Характеристика (σ1-σ3)/σ3 | Параметры модели (12) | ||
| n | d | a | |
| 1,5 | 100 | 1,0134 | 0,3722 |
| 1,94 | 100 | 4,3009 | 0,2895 |
| 2,83 | 100 | 3,1082 | 0,2141 |
| 4,6 | 100 | 0,8723 | 0,415 |
В табл. 2 и 3 приведены значения коэффициентов n, с, b и d модели (13) для расчета остаточной деформации, накапливаемой образцом из песчано-гравийной смеси.
Таблица 2 - Параметры b и c модели (13) для расчета остаточной деформации, накапливаемой образцом из песчано-гравийной смеси
| Характеристика (σ1–σ3)/σ3 | Параметр n | σ3≤40 кПа | σ3=70 кПа | σ3≥210 кПа | |||
| b | c | b | c | b | c | ||
| ≤0,5 | 100 | – | – | – | – | 0,073 | -0,84 |
| 1 | 100 | 0,072 | -0,832 | 0,085 | -0,818 | 0,071 | -0,865 |
| 1,5 | 100 | – | – | 0,071 | -0,809 | 0,074 | -0,742 |
| 2 | 100 | 0,065 | -0,871 | 0,060 | -0,915 | 0,056 | -0,741 |
| 3 | 100 | 0,079 | -0,699 | 0,071 | -0,861 | – | – |
| 4 | 100 | 0,072 | -0,656 | 0,079 | -0,805 | – | – |
| ≥5 | 100 | – | – | 0,046 | -0,505 | – | – |
Таблица 3 - Параметр d модели (13) для расчета остаточной деформации, накапливаемой образцом из песчано-гравийной смеси
| Характеристика (σ1–σ3)/σ3 | σ3≤40 кПа | σ3=70 кПа | σ3≥210 кПа |
| £0,5 | 1,734 | 0,895 | 0,378 |
| 1 | 1,566 | 0,883 | 0,611 |
| 1,5 | 1,397 | 0,871 | 0,770 |
| 2 | 1,229 | 0,920 | 0,644 |
| 3 | 0,682 | 0,887 | 0,611 |
| 4 | 2,457 | 2,295 | 2,019 |
| ³5 | 2,213 | 2,050 | 1,774 |
Аналогичные коэффициенты определены автором для расчета деформаций, накапливаемых грунтами и щебеночными материалами из различных пород (диабаза, гранодиорита, известняка, доломита и др.). Спектр материалов, к которым применимы модели (12) и (13) и для которых определены параметры моделей, велик. Поэтому для освещения параметров моделей (12) и (13) для различных материалов и разновидностей грунтов целесообразно посвятить отдельную публикацию, являющейся продолжением этой работы. В настоящей статье ограничимся данными, представленными в табл. 1 – табл. 3, а так же сопоставлением результатов расчета деформации, накапливаемой песчано-гравийной смесью с экспериментальными данными. Такое сопоставление приведено на рис. 3. Данные эксперимента и результаты расчета получены при величине минимального главного напряжения 40 кПа.
Из анализа данных рис. 3 следует, что предлагаемая нами обобщающая степенная модель (13) позволяет прогнозировать процесс накапливания пластической деформации с приемлемой точностью. Точность модели (12) так же можно считать удовлетворительной.
Исследование зависимости параметров материала, характеризующих их деформирование, от показателей физических свойств выполнено в работах [21, С. 11] и [12, С. 452]. Использование данных, полученных в этих работах, позволит определить зависимость параметров a(z), b(z), c(z)…m(z) формулы (2) от глубины. В этом случае подынтегральное выражение уравнения (2) превращается в сложную функцию. Для вычисления определенного интеграла сложной функции можно воспользоваться квадратурными формулами Симпсона, Ньютона–Котеса, Уэдля и т.п. Таким образом, вычисление определенного интеграла сложной функции не представляет затруднений.
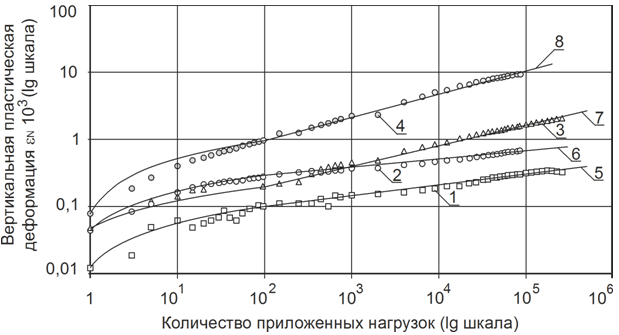
Рис. 3 - Зависимость вертикальной пластической деформации ПГС от числа нагрузок и напряжений при s3=40 кПа, 1 - 4 - эксперимент при (s1-s3)/ s3 1; 2; 3; и 4; при s3=40 кПа; 5 - 8 - расчет при (s1-s3)/ s3 1; 2; 3; и 4; при s3=40 кПа
Заключение
По материалам работы можно сформулировать выводы и задачи будущих исследований и публикаций:
- Установлено, что при воздействии циклической нагрузки в грунтах и дискретных материалах процесс накапливания пластической деформации имеет наследственных характер. Для определения приращения пластической деформации от n-го приложения нагрузки предложены степенные функции, которые рассматриваются как ядра интегральных уравнений наследственной теории.
- Интегрированием уравнений получены логарифмическая и степенная модели (12) и (13), которые обобщают ряд известных эмпирических формул и обладают большей точностью при расчете пластической деформации.
- Из анализа данных трехосных испытаний установлены коэффициенты предлагаемых моделей для широкого спектра щебеночных материалов и грунтов.
- Задачами дальнейших публикаций является:
– разработка методики и ее применение при определении параметров моделей (12) и (13) для различных материалов;
– разработка метода расчета вязкой составляющей пластической деформации eвпn, что позволит учитывать влияние продолжительности воздействия нагрузки, а значит скорости движения;
– разработка метода расчета пластического смещения поверхности покрытия и глубины неровностей, формирующихся в продольном и поперечном направлении.
Список литературы / References
- Герцог В.Н. Расчет дорожных одежд по критериям ровности. Часть 1. Обоснование норм ровности асфальтобетонных покрытий / В. Н. Герцог, Г. В. Долгих, В. Н. Кузин // Инженерно-строительный журнал. – 2015. – №5 (57) – С. 45-57.
- Bamrungwong C., et al. Development Of A Falling weight deflectometer (FWD) for evaluating the pavement conditions. Asian Transportation Research Society. Research Report Printed in Thailand. November, 2009. – 147 p.
- Александров А.С. Исследование пластического деформирования дискретных материалов при воздействии циклических нагрузок и определение параметров математических моделей / А. С. Александров // Строительные материалы. – 2016. – № 10. – С. 27-32.
- Barksdale R.D. Laboratory Evaluation of Rutting in Base course Materials. Proceedings of the 3-rd International Conference on Asphalt Pavements. London: 1972, pp. 161–174.
- Sweere G.T.H. Unbound granular bases of roads. // PhD thesis, Delft University of Technology, Delft, The Netherlands. 1990.
- Aleksandrov A.S., Semenova T.V., Aleksandrova N.P. Analysis of permanent deformations in granular materials of road structures. // Road and Bridges - Drogi i Mosty, 2016, Vol. 15, Pp 263 – 276.
- Arnold G.K. Rutting of Granular Pavements. // Thesis submitted to The University of Nottingham for the degree of Doctor of Philosophy, November 2004. – 417 p.
- Niemunis A., Wichtmann T., Triantafyllidis T. A high-cycle accumulation model for sand. // Computers and Geotechnics, 2005. Vol. 32, No4, Pp. 245-263.
- Niemunis A., Wichtmann T. (2014): Separation of time scale in the HCA model for sand. // Acta Geophysica, Vol. 62, No. 5, pp. 1127-1145.
- Werkmeister S. Permanent deformation behavior of unbound granular materials in pavement constructions // Ph.D. thesis, University of Technology, Dresden, The Germany. 2003.
- Семенова Т.В. Совешенствование методов экспресс контроля уплотнения грунтов в земляном полотне лесных дорог. Часть 1. Обобщающая математическая модель / Т. В. Семенова, Н. П. Александрова // Международный научно-исследовательский журнал. –2016.– № 6-2 (48). – С. 10-14.
- Семенова Т.В. Влияние влажности и степени уплотнения грунта земляного полотна на параметры прочности и деформируемости / Т. В. Семенова, Н. В. Кузин // Научный альманах. – 2016.– № 7-1 (21). – С. 451-454.
Список литературы на английском языке / References in English
- Gercog V.N. Raschet dorozhnyh odezhd po kriterijam rovnosti. Chast' 1. Obosnovanie norm rovnosti asfal'tobetonnyh pokrytij [Calculation of pavements for roughness criteria. Part 1. Justification standards evenness of asphalt-concrete coatings] / V. N. Gercog, G. V. Dolgih, V. N. Kuzin // Inzhenerno-stroitel'nyj zhurnal [Magazine of Civil Engineering]. – 2015. – №5 (57) – P. 45-57. [in Russian]
- Bamrungwong C., et al. Development Of A Falling weight deflectometer (FWD) for evaluating the pavement conditions. Asian Transportation Research Society. Research Report 2008. Printed in Thailand. November, 2009. – 147 p.
- Aleksandrov A.S. Issledovanie plasticheskogo deformirovanija diskretnyh materialov pri vozdejstvii ciklicheskih nagruzok i opredelenie parametrov matematicheskih modelej [A Generalizing model of plastic deformation of discrete materials of road structures under impact of cyclic loads] / A. S. Aleksandrov // Stroitel'nye materialy [Construction Materials]. – 2016. – № 10. – P. 27-32.[in Russian]
- Barksdale R.D. Laboratory Evaluation of Rutting in Base course Materials. Proceedings of the 3-rd International Conference on Asphalt Pavements. London: 1972, pp. 161–174.
- Sweere G.T.H. Unbound granular bases of roads. // PhD thesis, Delft University of Technology, Delft, The Netherlands. 1990.
- Aleksandrov A.S., Semenova T.V., Aleksandrova N.P. Analysis of permanent deformations in granular materials of road structures. // Road and Bridges - Drogi i Mosty, 2016, Vol. 15, Pp 263 – 276.
- Arnold G.K. Rutting of Granular Pavements. // Thesis submitted to The University of Nottingham for the degree of Doctor of Philosophy, November 2004. – 417 p.
- Niemunis A., Wichtmann T., Triantafyllidis T. A high-cycle accumulation model for sand. // Computers and Geotechnics, 2005. Vol. 32, No4, Pp. 245-263.
- Niemunis A., Wichtmann T. (2014): Separation of time scale in the HCA model for sand. // Acta Geophysica, Vol. 62, No. 5, pp. 1127-1145.
- Werkmeister S. Permanent deformation behavior of unbound granular materials in pavement constructions // Ph.D. thesis, University of Technology, Dresden, The Germany. 2003.
- Semenova T.V. Soveshenstvovanie metodov jekspress kontrolja uplotnenija gruntov v zemljanom polotne lesnyh dorog. Chast' 1. Obobshhajushhaja matematicheskaja model' [Improvement of methods for monitoring the express compacted soil subgrade forest roads] / T. V. Semenova, N. P. Aleksandrova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. –2016. – № 6-2 (48). – P. 10-14.[in Russian]
- Semenova T.V. Vlijanie vlazhnosti i stepeni uplotnenija grunta zemljanogo polotna na parametry prochnosti i deformiruemosti [Influence of moisture content and degree of compaction of subgrade on the parameters of strength and deformability] / T. V. Semenova, N. V. Kuzin // Nauchnyj al'manah [Science Almanac]. – 2016. – № 7-1 (21). – P. 451-454.[in Russian]
