МЕТОДИКА ОБРАБОТКИ РЕЗУЛЬТАТОВ ГИДРАВЛИЧЕСКОГО ЭКСПЕРИМЕНТА
Бенин Д.М.
ORCID: 0000-0003-1265-4071, Кандидат технических наук, Доцент кафедры информационных технологий, ФГБОУ ВО «РГАУ – МСХА им. К.А.Тимирязева»
МЕТОДИКА ОБРАБОТКИ РЕЗУЛЬТАТОВ ГИДРАВЛИЧЕСКОГО ЭКСПЕРИМЕНТА
Аннотация
Настоящая статья описывает методику обработки натурного эксперимента. В статье даются рекомендации, основанные на действующих нормативных документах в этой части, по применению статистических методов обработки данных эксперимента. Приводятся примеры по расчетам точности результатов измерений наиболее распространенных в экспериментальных исследованиях гидравлических параметров, таких как расход, давление и скорость. От правильности обработки полученных экспериментальных значений зависит их достоверность и возможность их дальнейшего использования.
Ключевые слова: гидравлический эксперимент, обработка данных эксперимента, погрешность измерений, расход, давление, скорость.
Benin D.M.
ORCID: 0000-0003-1265-4071, PhD in Engineering, Russian state agrarian University - MSHA named after K. A. Timiryazev
METHODS OF PROCESSING THE RESULTS OF HYDRAULIC EXPERIMENT
Abstract
This article describes the technique of processing a natural experiment. The article provides recommendations based on current regulations in this part, the use of statistical methods of processing of experimental data. Examples for the calculation of accuracy of measurement results the most common in experimental studies of hydraulic parameters such as flow, pressure and speed. From the correctness of processing of the experimental values is their reliability and the possibility of their further use.
Keywords: hydraulic experiment, processing of experimental data, measurement uncertainty, flow, pressure, speed.
Проведение любого натурного эксперимента состоит из таких этапов, как постановка цели и задачи эксперимента, планирование эксперимента, создание натурной модели, обработка полученных данных с помощью статистических методов, оценка точности результатов измерений. От правильности выбранной методики анализа данных зависит их достоверность и возможность дальнейшего апеллирования ими.
Статистическую обработку данных следует начинать с обнаружения и анализа выбросов. Стандартом [1] для этого рекомендуется применение критерия Граббса, при этом выделяют проверку на один и два выброса. Для проверки на один выброс наибольшего результата x данные ранжируют в порядке возрастания хi (i= 1, 2 … p) и вычисляют статистику Граббса Gp:
![]() (1)
(1)
где ![]() , р – максимальный ранг (ранжирование начинается с 1).
, р – максимальный ранг (ранжирование начинается с 1).
Для проверки значимости наименьшего результата вычисляют тестовую статистику:
![]() (2)
(2)
Критические значения для критерия Граббса приведены в Таблице 8 ГОСТ Р ИСО 5725-2 – 2002 [2].
Для проверки двух наибольших результатов на выбросы вычисляют статистику:
![]() (3)
(3)
где ![]()
Для проверки двух наименьших результатов на выбросы вычисляют статистику:
![]() (4)
(4)
где ![]()
После обработки выбросов следует проверить соответствие выборочного закона распределения теоретическому, для гидравлического эксперимента, как правило, нормальному, функция плотности вероятности которого имеет вид:
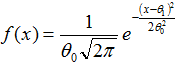 (5)
(5)
где θ0 и θ1 – параметры распределения (среднеквадратическое отклонение и математическое ожидание), х – значение случайной величины, ![]() .
.
Необходимо проверить сложную гипотезу о проверке принадлежности выборочного распределения нормальному закону, сложную, потому что оценки параметров нормального распределения θ0 и θ1 определены по той же выборке, по которой проверяют согласие. Нулевая гипотеза Н0 имеет вид:
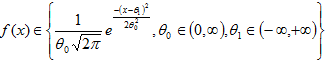 (6)
(6)
При проверке простых гипотез неaпараметрические критерии типа Колмогорова, Смирнова, ω2 и Ω2 Мизеса уступают по мощности критериям типа ![]() , особенно, если в последних используется асимптотически оптимальное группировании. Но при проверке сложных гипотез непараметрические критерии оказываются более мощными. и уже при n=15-20 можно, не опасаясь больших ошибок, пользоваться этими предельными законами при анализе данных. Мощность непараметрических критериев при проверке сложных гипотез при тех же объемах выборок n всегда существенно выше, чем при проверке простых.
, особенно, если в последних используется асимптотически оптимальное группировании. Но при проверке сложных гипотез непараметрические критерии оказываются более мощными. и уже при n=15-20 можно, не опасаясь больших ошибок, пользоваться этими предельными законами при анализе данных. Мощность непараметрических критериев при проверке сложных гипотез при тех же объемах выборок n всегда существенно выше, чем при проверке простых.
Для данных расчетов возможно использование критерия Крамера-Мизеса-Смирнова статистика которого имеет вид [1]:
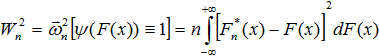 (7)
(7)
где ![]() - выборочное (расчетное) значение статистики омега-квадрат; Ψ - весовая функция; х – непрерывная случайная величина; F(x) – функция распределения непрерывной случайной величины; n – объем выборки;
- выборочное (расчетное) значение статистики омега-квадрат; Ψ - весовая функция; х – непрерывная случайная величина; F(x) – функция распределения непрерывной случайной величины; n – объем выборки;![]() - эмпирическая функция распределения.
- эмпирическая функция распределения.
Статистика![]() учитывает отклонение эмпирической функции распределения от теоретической при всех возможных значениях х исследуемой случайной величины Х.
учитывает отклонение эмпирической функции распределения от теоретической при всех возможных значениях х исследуемой случайной величины Х.
Заключительным этапов обработки результатов эксперимента является оценка точности результатов измерений, которую следует проводить согласно ГОСТ Р ИСО 5725-1-2002. Данный нормативный документ распространяется на методы измерения непрерывных величин, дающие в качестве результата измерений единственное значение. Согласно документу показатели точности должны определяться на основании серии результатов измерений. Расчеты стоит проводить для контрольной серии непосредственно измеряемых величин.
Предел повторяемости – значение, которое с доверительной вероятностью 0,95 не превышается абсолютной величиной разности между результатами двух измерений, полученными в условиях повторяемости. Сопоставление производится на основании более двух результатов измерений, полученных в одной лаборатории в условиях повторяемости. Для этого размах вариаций (хmax–xmin) результатов измерений каждой величины соотносится с критическим диапазоном для уровня вероятности 95% при числе измерений n: ![]() ,
,
где σr – стандартное отклонение повторяемости; f(n) – коэффициент критического диапазона, выборочные значения которого приведены в Таблице 1.
Таблица 1 - Коэффициенты критического диапазона f(n)
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| f(n) | 2.8 | 3.3 | 3.6 | 3.9 | 4.0 | 4.2 | 4.3 | 4.4 | 4.5 |
Если размах вариаций измеряемой величины меньше критического диапазона, то в качестве окончательного результата следует принимать среднее арифметическое значение результатов нескольких измерений. В противном случае в качестве окончательного результата должна фиксироваться медиана нескольких измерений.
Согласно ГОСТ ИСО 5725 точность метода измерений представляет собой функцию: ![]() (8)
(8)
где m – общее среднее значение (математическое ожидание); B - лабораторная составляющая систематической погрешности в условиях повторяемости; e – случайная составляющая погрешности результата измерений в условиях повторяемости.
Так как условия повторяемости и воспроизводимости в эксперименте, как правило, обеспечиваются для всех измерений, используется среднее арифметическое повторных наблюдений.
Точность измерений при проведении опытов зависит от точности наводки измерительного прибора и точности отсчета по прибору.
Рассмотрим оценку точности измерений каждого из этих параметров отдельно на конкретных примерах [3].
Измерение расходов производилось при помощи треугольного водослива. Ошибка в измерении расхода складывается из ошибок в измерении напора на водосливе, ошибки определения нуля установки водослива и ошибки при определении расхода по тарировочной кривой. Напор на мерном водосливе можно измерить шпитценмасштабом по уровню воды в пьезометрическом стакане. Наводка на уровень воды производится с точностью 0,05 мм. Привязка нуля мерного водослива была осуществлена с точностью 0,1 мм. Отсчеты по нониусу шпитценмасштаба производились также с точностью 0,1 мм. Таким образом, абсолютная предельная ошибка ∆h в определении напора на мерном водосливе составляет: ![]()
При снятии показаний с тарировочной кривой определение напора производилось по миллиметровой шкале с точностью 0,25 мм, т.е. абсолютная предельная погрешность в измерении напора при пользовании треугольным водосливом составила:![]()
Отсчеты расхода по тарировочной кривой производились также с точностью 0,25 мм. Масштаб расхода тарировочной кривой составлял 1л/сек в 10 мм, т.е. абсолютная ошибка в снятии отсчета расхода по шкале расходов составляла 0,025 л/сек. При измерении расходов от 4 до 8 л/сек одному сантиметру напора тарировочной кривой соответствовал расход около 0,8 л/с, т.е. предельной абсолютной ошибке измерении напора ![]() =0,5мм соответствует ошибка в измерении расхода:
=0,5мм соответствует ошибка в измерении расхода: ![]() ,
,
Таким образом, предельная абсолютная ошибка в измерении расхода по тарировочной кривой (систематическая ошибка) составляла BQ :
![]()
Границы доверительного интервала случайной ошибки e на основании контрольной серии опытов для доверительной вероятности Р=0.95 составляют eQ=0.029 л/сек.
Ошибка погрешности результатов измерений сравнима с ошибкой погрешности прибора, поэтому границы доверительного интервала случайной и неисключенной систематической погрешности составляют [4]:
![]()
Привязка шкалы пьезометрических щитов производилась с точностью 0,5 мм. Отсчеты уровней воды в пьезометрических трубках производились по низу мениска по миллиметровой шкале с абсолютной точность отсчета 0,5 мм. Предельная абсолютная ошибка в измерении пьезометрического уровня ВР (систематическая ошибка) составила Вр=1,0 мм. Величина давления ![]() , выраженная в высоте водяного столба, находилась в пределах от 17 до 150 см.
, выраженная в высоте водяного столба, находилась в пределах от 17 до 150 см.
Следовательно, можно считать, что давление ![]() в потоке было измерено с предельной относительной ошибкой порядка:
в потоке было измерено с предельной относительной ошибкой порядка:
![]()
Среднеквадратичное отклонение составляет: ![]() .
.
Границы доверительного интервала случайной ошибки на основании контрольной серии опытов для доверительной вероятности Р=0,95 составляют Δp=ep=0,251 мм, Bp=1мм. Ошибка погрешности результатов измерений сравнима с ошибкой погрешности прибора, поэтому границы доверительного интервала случайной и неисключенной систематической погрешности составили: ![]() .
.
Предельная относительная суммарная ошибка (систематическая и случайная) в измеряемом диапазоне давлений с вероятностью 0,95 будет принадлежать интервалу 0,1÷1,0 %.
Скорость потока u, измеренная трубкой Пито, определяется разностью показаний динамической и статической трубок: ![]()
Абсолютная предельная ошибка в определении скоростного напора складывается из ошибки в наведении на уровень жидкости в статической и динамической трубках и ошибки при взятии отсчета по нониусу микроманометра. Предельное значение каждой из этих ошибок составляло 0,1мм. Следовательно, предельная абсолютная ошибка в определении ![]() мм.
мм.
Предельная относительная ошибка зависит от величины измеряемой скорости потока. При тарировке изменение скорости находилось в пределах от 0,4 до 2 м/с, чему соответствовал перепад по микроманометру от 18 до 200мм. Этим значениям перепадов соответствует предельная относительная ошибка: ![]()
Предельная относительная ошибка в определении тарировочного коэффициента φ лежит в пределах ![]() .
.
При работе с трубкой Пито вторично накладывается ошибка в определении скоростного напора. В опытах изменение скорости находилось в пределах от 0,1 до 1,2м/с, чему соответствовал перепад по манометру от 4 до 350мм. Этим значениям перепадов соответствует предельная относительная ошибка от 5 до 0,1%. Таким образом, предельная относительная ошибка при определении скорости составляет: ![]()
Причем ошибка 4,4% относится к измерениям, которые имели место при малых скоростях потока. Среднеквадратичное отклонение составляет (1,5¸0,3)%.
Список литературы / References
- ГОСТ Р ИСО 5725-6-2002. Точность (правильность и прецизиозность) методов и результатов измерений. Использование значений точности на практике. – Введ. 2002-11-01. –М.: Изд-во стандартов, 2002, 42с.
- Р 50.1.037-2002. Прикладная статистика. Правила проверки опытного согласия с теоретическим. Непараметрические критерии. – Введ.2002-02-22., -М.: изд-во стандартов, 2002, 43с.
- Бенин Д.М. Гидравлическое обоснование параметров проточных частей стабилизаторов расхода трубчатых водопропускных сооружений. : дис. … канд. техн. наук : 05.23.16. защищена 20.06.11. : утв.27.12.11 / Бенин Дмитрий Михайлович. – М., 2011. – 175с.
- Снежко В.Л., Хусни И. Автоматизация напорных водопропускных сооружений мелиоративных гидроузлов. В сборнике: новые направления в решении проблем АПК на основе современных ресурсосберегающих, инновационных технологий. Материалы Международной научно-практической конференции, посвященной 65-летию Победы в Великой Отечественной войне. 2010. С. 264-266.
Список литературы на английском языке / References in English
- GOST R ISO 5725-6-2002. Tochnost' (pravil'nost' i precizioznost') metodov i rezul'tatov izmerenij. Ispol'zovanie znachenij tochnosti na praktike. [Accuracy (trueness and precisionist) of methods and measurement results. The use of precision values in practice]. – Vved. 2002–11–01. – M. : Izd-vo standartov, 2002. – 42 [in Russian].
- R 50.1.037-2002. Prikladnaja statistika. Pravila proverki opytnogo soglasija s teoreticheskim. Neparametricheskie kriterii. [Applied statistics. Validation rules experimental agreement with the theoretical. Non-parametric tests]. – Vved. 2002–02–22. – M. : Izd-vo standartov, 2002. – 42 [in Russian].
- Benin D.M. Gidravlicheskoe obosnovanie parametrov protochnyh chastej stabilizatorov rashoda trubchatyh vodopropusknyh sooruzhenij.[ Hydraulic substantiation of parameters of flowing parts of the tubular stabilizers flow culverts] : dis. … of PhD in Engineering : 05.23.16. defense of the thesis 20.06.11. : approved.27.12.11 / Benin Dmitrij Mihajlovich. – M., 2011. – 175p. [in Russian]
- Snezhko V.L., Husni I. Avtomatizacija napornyh vodopropusknyh sooruzhenij meliorativnyh gidrouzlov. V sbornike: novye napravlenija v reshenii problem APK na osnove sovremennyh resursosberegajushhih, innovacionnyh tehnologij. Materialy Mezhdunarodnoj nauchno-prakticheskoj konferencii, posvjashhennoj 65-letiju Pobedy v Velikoj Otechestvennoj vojne. [Automation of the discharge culverts and reclamation of a waterworks. In the collection: new directions in solving problems of agricultural sector based on modern resource-saving innovative technologies. Materials of International scientific-practical conference dedicated to the 65th anniversary of Victory in the great Patriotic war]. 2010, p.264-266. [in Russian]
