Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

КОРПУСКУЛЯРНО-ВОЛНОВЫЕ ПРОЦЕССЫ

Научная статья
Кораблев Г.А.
DOI:
https://doi.org/10.23670/IRJ.2017.57.105
Выпуск: № 3 (57), 2017
Опубликована:
2017/03/17
PDF

Кораблев Г.А.

Доктор химических наук, профессор, Ижевская государственная сельскохозяйственная академия

КОРПУСКУЛЯРНО-ВОЛНОВЫЕ ПРОЦЕССЫ

Аннотация

Два принципа сложения энергетических характеристик структурных взаимодействий выполняются, если процесс идет или по градиенту потенциала или против него. Трансформируя эти правила на корпускулярно-волной дуализм можно предположить, что корпускулярные взаимодействия имеют место по градиенту потенциала (принцип сложения обратных величин энергий), а волновые процессы идут против градиента потенциала (принцип алгебраического сложения энергий). Такой подход подтверждается эмпирическим уравнением, в котором акт квантового действия сводится к  перераспределению энергий в системе частица-волна.

Показано, что угловой вектор вращательно-поступательного движения электронов при квантовых переходах меняется в соответствии с квантовым числом квадрата тангенса этого угла.

Ключевые слова: градиент потенциала, квантовые переходы, корпускулярно-волновой дуализм, геодезический угол, тутовый шелкопряд.

Korablev G.A.

PhD in Chemistry, Izhevsk State Agricultural Academy

CORPUSCULAR-WAVE PROCESSES

Abstract

Two principles of adding energy characteristics of structural interactions are fulfilled if the process flows either along the potential gradient or against it. Transforming these rules onto the corpuscular-wave dualism, we can assume that corpuscular interactions flow along the potential gradient (principle of adding reciprocals of energies), and wave processes – against the potential gradient (principle of algebraic addition of energies). Such approach is confirmed by the empiric equation, in which the act of quantum action is narrowed to the energy redistribution in the system “particle-wave”. 

It is demonstrated that the angular vector of rotational-translation motion of electrons at quantum transitions changes in compliance with the quantum number of the square tangent of this angle. 

Keywords: potential gradient, quantum transitions, corpuscular-wave dualism, geodesic angle, silkworm.

Введение

Проблема квантово-волнового дуализма была в основном решена в период создания квантовой механики. Так, применение уравнения де-Бройля позволяет определить границы проявления таких явлений. Но какое свойство при этом доминирует зависит от условий процесса. И определить заранее какая часть из них будет работать в каждом конкретном случае достаточно сложно, хотя известно, что волновая картина чаще имеет место при низких энергиях, а корпускулярная – при высоких.

Один из основоположников квантовой механики Макс Борн по этому поводу сказал: «Каждый процесс может быть интерпретирован или с корпускулярной или с волновой точки зрения. Однако доказательство того, что мы имеем дело действительно с частицами или с волнами лежит за пределами наших возможностей, поскольку мы не в состоянии определить все характерные свойства процесса. Поэтому можно только сказать, что волновые и корпускулярные описания следует считать лишь как два дополняющих друг друга способа рассмотрения одного и того же объективного процесса». [7]

Таким образом, эти проблемные вопросы квантово-волнового дуализма нуждаются в дальнейшем исследовании и обсуждении. В данной работе делается попытка пояснения их с позиции представлений о пространственно-энергетических взаимодействиях.

  1. О двух принципах сложения энергетических характеристик взаимодействий

Анализ кинетики разнообразных физико-химических процессов показывает, что во многих случаях складываются обратные величины скоростей, кинетических или энергетических характеристик соответствующих взаимодействий.

В частности, такое предположение подтверждается формулой вероятности процесса переноса электрона (W∞) за счет перекрывания волновых функций 1 и 2 (в стационарном состоянии) при электронно-конформационных взаимодействиях:

09-03-2017 10-01-19   (1)

Уравнение (1) используется при оценке характеристик процессов диффузии, сопровождающейся безизлучательными переносами электронов в белках [9].

А так же: «Из классической механики известно, что относительное движение двух частиц с энергией взаимодействия U(r) происходит как движение материальной точки с приведенной массой μ:

09-03-2017 10-02-57  (2)

в поле центральной силы U(r), а общее поступательное движение – как свободное движение материальной точки с массой:

09-03-2017 10-03-54     (3)

Такое положение вещей имеет место и в квантовой механике» [3].

Для движущихся термодинамических систем первое начало термодинамики имеет вид:

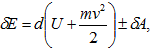09-03-2017 10-04-29  (4)

где: δE – количество энергии, сообщенное системе;

член 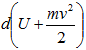09-03-2017 10-05-34 – характеризует изменения внутренней  и кинетической энергий системы;

+ δA – работа, выполненная системой;

- δA – работа, совершенная над системой.

Так как величина работы численно равна изменению потенциальной энергии, то:

09-03-2017 10-10-07  (5,6)

Вероятно, не только в термодинамических, но и во многих других процессах в динамике взаимодействия движущихся частиц важно не только значение потенциальной энергии, а ее изменение. Поэтому должно выполняться для двухчастичных взаимодействий:

09-03-2017 10-10-58  (7)

Здесь

09-03-2017 10-11-49   (8)

где U2 и U1 – потенциальные энергии системы в конечном и начальном состояниях.

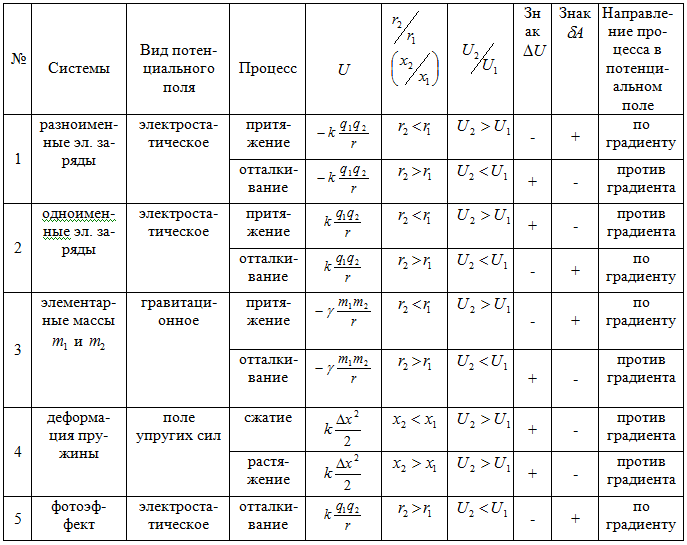
Был проведен анализ характера изменения величины потенциальной энергии (ΔU) по ее знаку для различных потенциальных полей, приведенный в табл. 1.

Из таблицы видно, что значения – ΔU и соответственно + δA (положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а ΔU и -δA (отрицательная работа) имеют место при взаимодействиях против градиента потенциала.

Решение двухчастичной задачи взаимодействий двух материальных точек с массами  m1  и  m2, полученное при условии отсутствия внешних сил, соответствует взаимодействиям, которые идут по градиенту, работа положительная, совершается системой (аналогично процессу притяжения в гравитационном поле).

Решением этого уравнения через приведенную массу (μ) является уравнение Лагранжа для относительного движения изолированной системы двух взаимодействующих материальных точек с массами  m1 и  m2, которое в координате  х  имеет вид:

09-03-2017 10-16-12

Здесь U – взаимная потенциальная энергия материальных точек;  – приведенная масса.  

Таблица 1 – Направленность процессов взаимодействий

09-03-2017 10-17-15

При этом х″ = a (характеристика ускорения системы). Для элементарных участков взаимодействий ∆х можно принять:

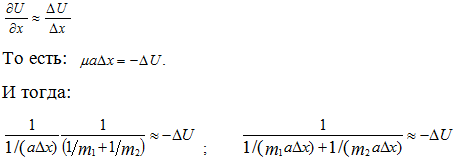09-03-2017 10-18-46 (9)

Или:

09-03-2017 10-19-33  (10)

где ∆U1 и ∆U2 – потенциальные энергии материальных точек на элементарном участке взаимодействий, ∆U – результирующая (взаимная) потенциальная энергия этих взаимодействий.

Таким образом:

  1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия находится по принципу сложения обратных значений соответствующих энергий подсистем [13]. Аналогично рассчитывается приведенная масса для относительного движения изолированной системы двух частиц.
  2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также – соответствующих энергий подсистем (аналогично гамильтониану).

Из уравнения (10) следует, что результирующая энергетическая характеристика системы такого взаимодействия двух материальных точек находится по принципу сложения обратных величин исходных энергий взаимодействующих подсистем.

«Электрон с массой m, движущийся около протона с массой М, эквивалентен частице с массой:  09-03-2017 10-20-44». [10] – стр. 12.

Поэтому, модифицируя уравнение (10), можно предположить, что энергия валентных орбиталей атома (ответственная за межатомные взаимодействия) может быть рассчитана [12] по принципу сложения обратных величин некоторых исходных энергетических составляющих, согласно уравнений:

09-03-2017 10-21-52 (11), (12), (13)

здесь: Wi – орбитальная энергия электронов [14]; ri – орбитальный радиус i–ой орбитали [15]; q=Z*/n* - по [11], ni – число электронов данной орбитали, Z*и n* - эффективный заряд ядра и эффективное главное квантовое число, r – размерные характеристики связи.

Для свободного электрона  P=Pе=Wr, где W = 0,510034 МэВ = 0,81872˟10-13 Дж.

В качестве размерной характеристики была использована величина классического радиуса электрона r = 2,81794˟10-15м и поэтому Ре = 2,30712˟10-28 Дж˟м.

  1. Акт квантового действия

Формализм уравнений (10,11,12) не является принципиально новым. Еще в 1924 году по эффекту Комптона было получено уравнение:

09-03-2017 10-24-01 (14)

Здесь: hν' – энергия рассеянного фотона, hν – энергия падающего фотона, mc2 – собственная энергия электрона, ϴ – угол рассеяния. При этом энергия фотонов уменьшается на величину, которую получил дополнительно электрон. Так происходит акт квантового действия, результатом которого является перераспределение энергии между корпускулярными и волновыми свойствами взаимодействующих систем.

Еще проще, если акт действия имеет место при взаимодействии пары одноименных частиц. При взаимодействии по градиенту потенциала (корпускулярный механизм) результирующая энергия в этом варианте 09-03-2017 10-25-19. Если процесс идет против градиента (волновое движение), то суммарная энергия Wв = 2W. Соотношение между ними 09-03-2017 10-25-43=4.

Электрический ток – это движение электронов по градиенту потенциала. Если предположить, что создаваемое им магнитное поле – это волновой процесс, то соотношение электрической и магнитной постоянных должно содержать эту цифру 4, что подтверждается в следующем эмпирическом уравнении:

09-03-2017 10-26-24   (15)

здесь: ɛ – электрическая постоянная, µ – магнитная постоянная, h – постоянная Планка, α – постоянная тонкой структуры – параметр характеризующий взаимодействия квантованных электронно-позитронного и электромагнитного полей. Число π определяется соотношением между вращательным движением (длина окружности) и поступательным движением (длина диаметра).

Относительная погрешность расчетов по этому уравнению составляет около 0,06%.

Коэффициент пропорциональности в уравнении (15) имеет размерность скорости ( м/с) для соотношения (Ф/Гн), т.е. таким образом характеризуется скорость перераспределения энергий в системе частица – волна.

Поэтому акт квантового действия, выраженный через постоянную Планка, сводится к равновесно-обменному перераспределению энергии между корпускулярными и волновыми процессами.

Обобщая формализм уравнений (10,15) на все другие взаимодействия происходящие по градиенту потенциала можно сделать вывод, что в этих случаях идут корпускулярные процессы, а волновой дуализм соответствует взаимодействиям против градиента потенциала.

  1. Угол электронной намотки

Известно, что частица может иметь три основные виды движений: поступательное, вращательное и колебательное. Но квантовая механика вопрос о траектории электрона не рассматривает, т.к. можно говорить лишь о вероятности нахождения его в данной точке пространства.

Но электрон движется и если это поступательное движение идет по градиенту потенциала, то оно может соответствовать корпускулярному процессу, а вращательное движение – волновому. Соотношение их актов перераспределения энергии зависит от величин исходных энергетических критериев подсистем. При квантовых переходах это могут быть орбитальные энергии связи соответствующих уровней.

Таким образом, основными параметрами квантовых переходов являются:

  1. Энергия электромагнитной волны квантового перехода согласно уравнения Планка E = hν, где ν – частота электромагнитной волны. Так в квантовых переходах проявляет себя колебательное движение, поскольку сама электромагнитная волна есть процесс распространения соответствующих колебаний.
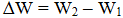
  2. Разность энергий связи электронов на разных энергетических уровнях перехода: 09-03-2017 10-29-05
  3. Результирующая энергия их корпускулярного взаимодействия:
image069  (16)

Рассмотрим некоторые важные в данном случае макропроцессы. Тутовый шелкопряд наматывает естественную (органическую) шелковую нить только под определенным углом вращения. В космонавтике на металлический цилиндр космического корабля наматывают целлюлозно-вискозную нить по специальной технологии и что важно под тем же углом намотки что и у тутового шелкопряда. Получается наиболее прочный, технологически более качественный и более легкий аппарат [4]. Можно говорить и о других примерах такого явления.

Этот угол (в основном – применительно к органическим системам) получил название геодезического угла: φг = 54,73º = 54º44'.

В общем случае угол намотки (ϴ) – это угол между геодезической линией и вектором вращательно движения. Геодезическая линия – это кратчайшее расстояние между двумя точками в геометрической фигуре вращения. Кстати, планеты вращаются вокруг солнца тоже по геодезической линии. Для пяти планет солнечной системы угол между осью вращения и орбитой равен от 62º до 66,5º. Земное ϴ, учитывающее видимо, и влияние Луны составляет 66º33'. Такая же величина ϴ имеется у Солнца. В астрономических терминах: наклонение эклиптики Солнца и наклонение экватора Земли к орбите численно одинаковы и равны 22º27'. Не в этом ли причина особой эффективности солнечного воздействия именно на земные биофизические процессы?

Основными элементами органических материалов являются азот, кислород, водород и главное углерод. Углерод специфический элемент, способный к более легкой гибридизации атомных орбиталей с квантовым переходом 2s-2p. Поэтому при повышении температуры и давления в органических материалах создаются условия для такой гибридизации атомов углерода, что, по-видимому,  и происходит при технологии намотки в космических аппаратах. А в тутовом шелкопряде, как и во многих других природных процессах, идут соответствующие ферментативные реакции, на которых мы еще учимся, как надо работать.

Для расчета ϴ и φг используем формализм комптоновского уравнения (14), модифицируя его применительно к квантовым переходам:

image070  (17)

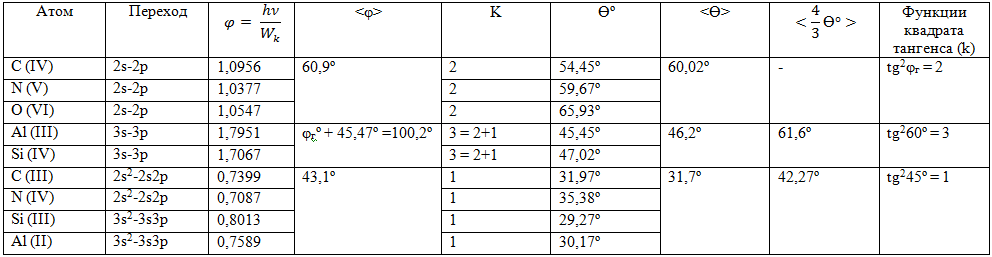
По этому уравнению разность энергий волнового и корпускулярного процессов численно равна разности энергий связи электронов на соответствующих орбиталях, но при выполнении принципов сложения (в данном случае  – вычитания) обратных величин этих параметров и с учетом квантовой геометрии переходов. Это и есть в соответствии с законом сохранения энергии процесс перераспределения ее при акте квантового действия. Угол ϴ – это угловой вектор движения электрона, который квантуется целым числом (K) через квадрат тангенса этого угла: tg2φг = 2; tg260º = 3; tg245º = 1.

Расчеты по уравнению (17) приведены в таблицах 2 и 3. При этом значения угла ϴ в основном коррелируют с величиной image071 по табл. 3.

В работах [2,4,8] используются понятия разрушающего напряжения при растяжении пластика на шаг его намотки: σα – осевое, σβ – окружное напряжения, которые заменяются пропорциональной им величиной Nα – осевое «усилие» и Nβ – окружное «усилие». При этом выполняется уравнение

image072  (18)

«Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия» [4].

Квантовые функции квадрата тангенса k = 1, 2, 3 численно определяют  соотношения двух катетов треугольника, значения которых через осевые и окружные напряжения характеризуют энергетические зависимости в системе с квантовыми и волновыми процессами.

Из таблицы 3 видно, что квантовые переходы типа 2s-2p для атома углерода в отличие от всех других элементов не сопровождаются изменением геодезического угла и коэффициента k. Очевидно, это свойство предопределяет уникальные особенности влияния геодезического угла намотки на стабильность биосистем. Кроме того, во всех переходах (кроме 2s-2p) выполняется соотношение  image073, что свидетельствует о том, что такой коэффициент в основном компенсирует структурные особенности более сложных переходов.

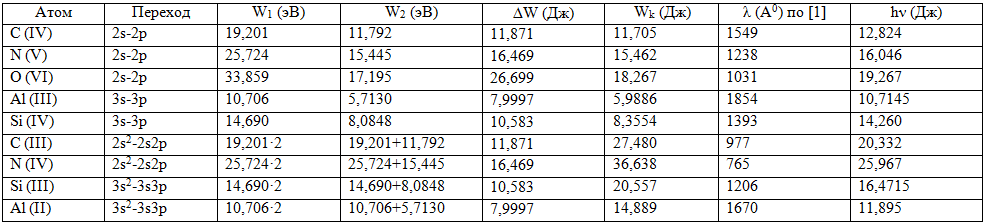
Таблица 2 – Энергии квантовых переходов

09-03-2017 10-36-07

Таблица 3 – Квантование геометрии структурных переходов

09-03-2017 10-36-35

Некоторая разница между значениями углов φ и ϴ или φ и  очевидно определяется эффектом рассеяния частиц вокруг основных координатных осей. Аналогично, при конформации клеточных структур частицы статистически концентрируется вдоль координатных осей гексагонов с отклонениями на 2,6º; 4,4º и 7,9º (рис. 1 по [6]).

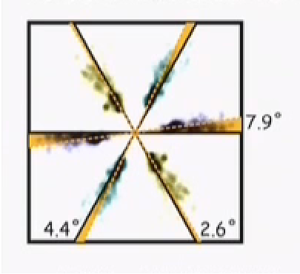
image077

Рис.1 – Статистическое распределение числа клеток вдоль координатных осей [6]

 

Среднее число таких отклонений, равное  4,97 примерно соответствует разности 60º – φгº = 5,27º.

Динамика гексагонального формирования клеточных систем находится в соответствии с установленным [5] условием примерного равенства пространственно-энергетических характеристик подсистем по всем линиям связи. Этому способствует и тот факт, что биосистемы, имеющие в своих структурах элементы второго периода дают угловой вектор намотки (ϴ) равный 60º.

Выводы

  1. Два принципа сложения энергетических характеристик структурных взаимодействий можно трансформировать на процессы корпускулярно-волнового дуализма.
  2. Предполагается, что при вращательно-поступательном движении электрона происходит перераспределение энергий в системе частица-волна, что проявляется через угловой вектор такого движения (угол намотки).
  3. Полученные зависимости дают возможность с единых позиций рассматривать разнородные по природе и по масштабам многие структурно-динамические процессы. Например, характеристика спин-орбитального взаимодействия – постоянная тонкой структуры 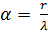image078, где r – классический радиус электрона, λ – его комптоновская длина волны.

Формально, но аналогично: сила взаимодействия двух длинных проводников с током пропорционально отношению  image079, где l – длина проводников, r – расстояние между ними.

  1. В этих примерах как и во многих других данный подход позволяет оценивать структурные взаимодействия, исходя из соотношений корпускулярных и волновых пространственно-энергетических параметров в каждом акте действия.
  2. В материаловедении и в физико-химических исследованиях, рассчитывая угол электронной намотки в некоторых структурах, можно делать конкретные рекомендации по инновационным технологиям, например, при изготовлении двигателей (в машиностроении) или при намотке на основу льна-долгунца (в сельском хозяйстве).
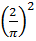  3. Разность фаз электрических и магнитных колебаний в электромагнитной волне составляет image080. Введя в коэффициент уравнения (15) величину image081, получаем уравнение для постоянной Планка с точностью, близкой к точности самих исходных данных:
image082  (15а)

где а = 0,0023293 – экспериментальная квантовая поправка к спиновому

gs – фактору электрона.

Список литературы / References

  1. Аллен К.У. Астрофизические величины / К.У. Аллен // М.: Изд. «МИР», 1977. – 446 с.
  2. Аюшеев Т.Ю. Геометрические вопросы адаптивной технологии изготовления конструкций намоткой из волокнистых композиционных материалов / Т.Ю. Аюшеев // Улан-Удэ: Изд-во БНЦ СО РАН, 2005. – 212с.
  3. Блохинцев Д.И. Основы квантовой механики / Д.И. Блохинцев // Изд. В.ш., 1961. – 512 с.
  4. Кодолов В.И. Полимерные композиции и технология изготовления из них двигателей летательных аппаратов / В.И. Кодолов // Ижевский механический институт, 1992. – 200 с.
  5. Кораблев Г.А., Васильев Ю.Г., Заиков Г.Е. Гексагональные структуры в наносистемах / Г.А. Кораблев // Химическая физика и мезоскопия. – 2015. Т. 17. №3. С. 424–429.
  6. Мозер Эдвард. Нобелевская лекция по физиологии: 11.03.2015 г. по телеканалу «Наука».
  7. Мэрисон Дж. Б. Общая физика с биологическими примерами / Дж. Б. Мэрисон // М.: Высш. школа, 1986. – 623 с.
  8. Пидгайный Ю.М., Морозова В.М., Дудко В.А. Методика расчета характеристик геодезической намотки оболочек тел вращения / Ю.М. Пидгайный // Механика полимеров. – 1967.– № 6. – С. 1096-1104.
  9. Рубин А.Б. Биофизика. Кн.1. Теоретическая биофизика / А.Б. Рубин // М.: В.ш.., 1987. – 319 с.
  10. Эйринг Г., Уолтер Дж., Кимбал Дж. Квантовая химия / Г. Эйринг // М., и. л., 1948. – 528 с.
  11. Clementi E., Raimondi D.L. / E. Clementi // J.Chem. Phys., 1963, v.38, №11, 2686-2689, J. Chem. Phys. – 1967. V.47. № 4. P. 1300–1307.
  12. Korablev G.A. Spatial-Energy Principles of Complex Structures Formation, Netherlands, Brill Academic Publishers and VSP, 2005. – 426 p. (Monograph).
  13. Korablev G.A., Zaikov G.E. Quantum and Wave Characteristics of Spatial Energy Interactions. Bioscience Methodologies in Physical Cemistry / G.A. Korablev // Apple Academic Press, 2013. – P. 130-143.
  14. Fischer C.F. Atomic Data / C.F. Fischer // 1972. № 4. P. 301–399.
  15. Waber J.T., Cromer D.T. // J.Chem. Phys. – 1965. V 42. № 12. P. 4116–4123.

Список литературы на английском языке / References in English

  1. Allen K.U. Astrofizicheskie velichiny [Astrophysical magnitudes] / K.U. Allen // M.: Izd. «MIR» [М.: Мir], 1977. – 446 p. [in Russian]
  2. Ayusheev T.YU. Geometricheskie voprosy adaptivnoj tekhnologii izgotovleniya konstrukcij namotkoj iz voloknistyh kompozicionnyh materialov [Geometric aspects of adaptive technology of manufacturing structures wound from fiber composite materials] / T.YU. Ayusheev // Ulan-Udeh: Izd-vo BNC SO RAN [Ulan-Ude: Publishing House of BSC SB RAS], 2005. – 212 p. [in Russian]
  3. Blohincev D.I. Osnovy kvantovoj mekhaniki [Principles of Quantum Mechanics] / D.I. Blohincev // Izd. V.sh. [Ed. VS.], 1961. – 512 p. [in Russian]
  4. Kodolov V.I. Polimernye kompozicii i tekhnologiya izgotovleniya iz nih dvigatelej letatel'nyh apparatov [The polymer compositions and manufacturing techniques of these aircraft engine] / V.I. Kodolov // Izhevskij mekhanicheskij institut [Izhevsk Mechanical Institute], 1992. – 200 p. [in Russian]
  5. Korablev G.A., Vasil'ev YU.G., Zaikov G.E. Geksagonal'nye struktury v nanosistemah [The hexagonal structure in the nanoscale] / G.A. Korablev // Himicheskaya fizika i mezoskopiya [Chemical Physics and mezoskopiya]. – 2015. V. 17. №3. P. 424–429. [in Russian]
  6. Mozer EHdvard. Nobelevskaya lekciya po fiziologii [Nobel Lecture in Physiology]: 11.03.2015 g. po telekanalu «Nauka». [in Russian]
  7. Mehrison Dzh. B. Obshchaya fizika s biologicheskimi primerami [General physics and biological examples] / Dzh. B. Mehrison // M.: Vyssh. Shkola [M .: Higher. school], 1986. – 623 p. [in Russian]
  8. Pidgajnyj YU.M., Morozova V.M., Dudko V.A. Metodika rascheta harakteristik geodezicheskoj namotki obolochek tel vrashcheniya [Procedure of characteristics of a geodesic winding shells rotating bodies] / YU.M. Pidgajnyj // Mekhanika polimerov [The mechanics of polymers]. – 1967.– № 6. – P. 1096-1104. [in Russian]
  9. Rubin A.B. Biofizika. Kn.1. Teoreticheskaya biofizika [Biophysics. Book 1. Theoretical biophysics] / A.B. Rubin // M.:V.sh.., 1987. – 319 p. [in Russian]
  10. EHjring G., Uolter Dzh., Kimbal Dzh. Kvantovaya himiya [Quantum chemistry] / G. EHjring // M., i. l., 1948. – 528 p. [in Russian]
  11. Clementi E., Raimondi D.L. / E. Clementi // J.Chem. Phys., 1963, v.38, №11, 2686-2689, J. Chem. Phys. – 1967. V.47. № 4. P. 1300–1307.
  12. Korablev G.A. Spatial-Energy Principles of Complex Structures Formation, Netherlands, Brill Academic Publishers and VSP, 2005. – 426 p. (Monograph).
  13. Korablev G.A., Zaikov G.E. Quantum and Wave Characteristics of Spatial Energy Interactions. Bioscience Methodologies in Physical Cemistry / G.A. Korablev // Apple Academic Press, 2013. – P. 130-143.
  14. Fischer C.F. Atomic Data / C.F. Fischer // 1972. № 4. P. 301–399.
  15. Waber J.T., Cromer D.T. // J.Chem. Phys. – 1965. V 42. № 12. P. 4116–4123.