METHOD OF CALCULATING THE STRESS-STRAIN STATE OF FRAME STRUCTURES OF AUTOTRACTOR TRAILERS OF CATEGORY О3 AT VARIOUS EXTERNAL INFLUENCES

Шермухамедов А.А.¹, Тогаев А.А.²

¹Доктор технических наук, профессор,

²Аспирант,

Ташкентский автомобильно-дорожный институт

МЕТОДИКА РАСЧЕТ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ РАМНЫХ КОНСТРУКЦИЙ АВТОТРАКТОРНЫХ ПРИЦЕПОВ КАТЕГОРИИ О3 ПРИ РАЗЛИЧНЫХ ВНЕШНИХ ВОЗДЕЙСТВИЯХ

Аннотация

В статье на примере тракторного прицепа, грузоподъемностью 4 тонн рассматривается методика численного расчета напряженно-деформируемого состояния рамных конструкций автотракторных прицепов категории О3. На основе сопоставительного анализа, показано, что предложенная методика расчета напряженно-деформируемого состояния рамы даёт хорошее согласование с экспериментальными данными (максимальные значения напряжения в пределах 11%) и ее можно использовать при обосновании прочностных параметров автотракторных прицепов категории О3.

Ключевые слова: прицеп, рама, численный расчёт, дорожные условия, прочность, напряженно-деформируемое состояние.

Shermukhamedov A.A.¹, Тоgаеv A.A.²

¹Doctor of Technical Sciences, professor,

²Postgraduate student,

Tashkent Automobile and Road Institute

METHOD OF CALCULATING THE STRESS-STRAIN STATE OF FRAME STRUCTURES OF AUTOTRACTOR TRAILERS OF CATEGORY О3 AT VARIOUS EXTERNAL INFLUENCES

Abstract

In article on an example of the tractor trailer, load-carrying capacity of 4 tons considers the technique for numerical calculating the stress-strain state of the frame structures of autotractor trailers of category O3. On the basis of the comparative analysis, it is shown, that the offered method of calculating the stress-strain state of the frame gives the good coordination with experimental data (the maximum values of pressure within 11 %) and it can be used at a substantiation durability parameters of autotractor trailers of category О3.

Keywords: trailer, frame, numerical calculation, road conditions, strength, stress-strain state.

Рама транспортной машины является основным несущим элементов конструкции, который воспринимает все нагрузки, возникающие при движении транспортного средства по дорогам и пересеченной местности. Кроме того, несущая система является основанием для крепления узлов и агрегатов машины, поэтому к ней предъявляются дополнительные требования и ее конструктивные формы должны быть подчинены общему компоновочному замыслу [1]. Расчёт рам на прочность является одной из важнейших задач при проектировании транспортных машин. Для того чтобы подчеркнуть актуальность проводимых исследований, отметим, что транспортное машиностроение, к сфере которого относится объект исследований, существенно отличается от других отраслей машиностроения. Его особенность состоит в том, что внешние нагрузки, действующие на конструкцию, переменны во времени и прилагаются с определенной частотой, зависящей от скорости движения, фактической нагрузки, состояния дороги и от многих других факторов. При этом во время эксплуатации возможны резонансные явления, которые могут привести к высоким, по отношению к номиналу, напряжениям и ко многим другим нежелательным явлениям. Переменный характер внешних нагрузок ведет к периодическому изменению напряжения, что, в свою очередь, способствует возникновению усталостных трещин, рост и развитие которых вызывает усталостное разрушение.

В работе на примере тракторного прицепа, грузоподъемностью 4 тонн  рассматривается методика расчета напряженно-деформируемого состояния рамы прицепа. Предложенная методика позволит проведения прочностных расчетов разрабатываемых на Ташкентском тракторном заводе автотракторных прицепов, грузоподъемностью 6 и 8 тонн.

Рама состоит из двух лонжеронов и семи поперечин, которые представляют собой жесткие стержневые элементы замкнутого и незамкнутого контура и имеют довольно корытные тонкостенные профили поперечного сечения (рис. 1). Указанные элементы получены штамповкой из листового металла толщиной 4-6 мм. Рамы прицепов конструктивно выполняются по следующей компоновке: лонжероны соединены между собой поперечинами посредством сварки, образуя при этом рамную конструкцию; в передней части рамы изготавливается опорно-сцепной устройство; подвеска соединяется с лонжеронами с помощью рессор, упругих элементов.

Рис. 1 - Общий вид рамы автотракторного прицепа

Актуальным является совершенствование методики расчетов на прочность и жесткость рамных конструкций прицепов. В качестве частных задач в работе рассматриваются: разработка расчетной схемы рамы по методу конечных элементов (МКЭ) с учетом симметрических свойств конструкции относительно продольной оси; исследование напряженно-деформированного состояния (НДС) рамы прицепа по условию статического нагружения; деформация изгиба рамы от внешней нагрузки, соответствующей номинальной грузоподъемности прицепа; совместная деформация рамы от массы груза и закручивания относительно опорного устройства при переезде колесом (стороной) через препятствие; учет податливости (осадки) упругих элементов подвески (рессор) на НДС рамы; сравнение расчетов по оценке НДС с результатами экспериментальных исследований для условий статического нагружения, выполненных на полигоне Узбекского государственного центра испытаний техники и технологий, при испытании прицепа 2ПТС-4-793А.

Рама рассматривается на упругом основании в условиях статического нагружения, обеспечивает соответствие характера распределения напряжений в конструкции, полученных расчетным путем, результатам проведенных экспериментальных измерений тензометрированием [2].

Величина внешней нагрузки, принятая к рассмотрению при исследовании НДС рамы, соответствует номинальной грузоподъемности прицепа.

При определении расчетной нагрузки рамы прицепа по статической прочности, с достаточной для инженерной и конструкторской практики погрешностью, нагруженность оценивается по деформациям изгиба от массы перевозимого груза. Влияние закручивания рамы, вызванное движением по неровной поверхности и перераспределением массы, учитывается включением в систему уравнений изгиба дополнительных уравнений кручения.

При построении расчетной схемы тонкостенного стержня рассматривают его «срединную» поверхность, которая проходит через средину элементов, образующих стержень [3]. След срединной поверхности в плоскости поперечного сечения образует профиль сечения (рис. 2).

Рис. 2 - Расчетная схема

По очертанию профиля различают два типа стержней:

− стержни с закрытым профилем;

− стержни с открытым профилем.

Для открытого и замкнутого профиля геометрические параметры определяется по формуле

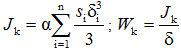                                          (1)

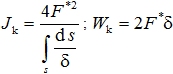                                            (2)

где α – коэффициент (для двутавров принимается равным 1,2; для швеллера – 1,12; уголка – 1,0); δ – соответственно толщина каждой части профиля (меньшая сторона прямоугольника); s – соответственно длина контура каждой части поперечного сечения (большая сторона прямоугольника); F^*– площадь «живого» поперечного сечения.

Работа тонкостенных стержней замкнутого профиля существенно не отличается от работы обычных стержней. При их расчетах можно применять закон плоских сечений. Работа тонкостенных стержней открытого профиля не может быть описана законом плоских сечений, он заменяется более сложным законом [4].

Поперечные сечения тонкостенных стержней открытого профиля при нагрузках, создающих закручивание, не остаются плоскими. Происходит депланация сечений, связанная с перемещениями точек из плоскости поперечного сечения вдоль оси стержня.

Расчет ведется в соответствии с известными правилами теории сопротивления материалов в следующей последовательности [5]:

а) рассчитывается эпюра изгибающих моментов;

б) определяются напряжения изгиба по формуле:

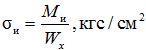
Из курса сопротивления материалов нам известно, что дифференциальное уравнение изгиба имеет вид

                                                       (3)

где ϕ_x – угол поворота сечения x, а M_x - изгибающий момент в сечении x.

Определим выражения для Q₁,M₁,Q₂, M₂ (рис. 3)

Рис. 3 - Схема сил и моментов, действующих на стержневой элемент

Из рис. 3 видно, что изгибающий момент в сечении x равен, M_x=Q₁·x+ M₁, теперь решая дифференциальное уравнение (3) получим

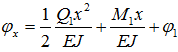
Прогиб v_x в сечении x определим из уравнения

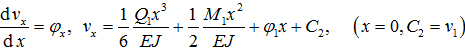
Запишем выражения ϕ_x и v_x при x=l

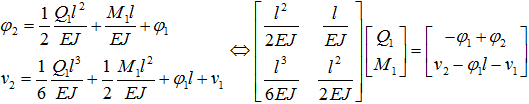
Решая систему получим

В конце балки Q₂=Q₁, M₂=Q₁·l+ M₁ выражения для Q₁,M₁,Q₂, M₂ можно записать в матричном виде

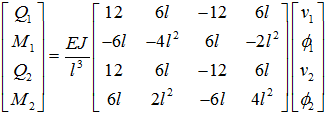                                   (4)

Стержневой элемент с учетом кручения рассматривается, как объединение элементов описывающих: изгиб в плоскости xy уравнениями (4) и кручение с осью симметрии x-x следующими уравнениями

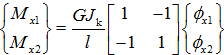
Тогда общая система уравнений примет вид:

         (5)

Запись уравнений (5) в матричном виде очень удобно при программировании, так как задачи по МКЭ сводятся к решению системы линейных уравнений [6].

Расчет ведется в упругой постановке с учетом жесткости рессоры.

При расчетах, должны учитываться специфические дорожные условия хлопкосеющих республик [1,7], для которых были приняты четыре категории дорожных участков.

1. Дорога с гудронным покрытием удовлетворительного качества, имеющая малоизношенные участки с среднестатической высотой неровности .
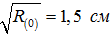2. Дорога с гравийным покрытием с изношенными участками с среднестатической высотой неровности .
3. Поворотная полоса с грядами высотой 8-12 см и шагом 90 см.
4. Глубокий кювет глубиной 40-45 см и шириной 100-150 см.

В качестве критерия, определяющего напряженное состояние рамы тракторного прицепа принято напряжение от действия на раму вертикальных динамических нагрузок, вызывающих изгиб элементов рамы прицепа в вертикальной плоскости приводящих к появлению нормальных напряжений

 

Скорость движения тракторного поезда, на основании ряда исследований [7, 8] и конструктивных особенностей хлопководческого трактора, по трем типам дорог была выбрана соответственно 23,12 км/ч, 13,2 км/ч и 9,25 км/ч, а при переезде глубокого кювета 6,1 км/ч.

Переезд через неровности в расчетной методики, учитывалось посредством изменения характеристик опорной поверхности колес. При этом рассматривались следующие четыре случая, соответствующие категориям дорожных условий:

1- все четыре колеса контактируют с поверхностью, нагрузка распределена равномерно; 2- все четыре колеса контактируют с поверхностью, нагрузка распределена неравномерно; 3- переднее левое колесо или заднее левое колесо не контактирует с опорной поверхностью; 4- переднее левое и заднее правое колеса не контактирует с опорной поверхностью.

На рис. 4. приведены значения нормальных напряжений в узлах лонжерона при нагрузке 4 тонн и максимальных значениях сжатия и растяжения волокон. Экспериментальные значения получены при скоростях движения 23,12 км/час, 13,2 км/час, 9,25 км/час.

При расчетах приняты: для положения 1 (рис.4. а и б) Р₂=Р₂₄=Р₇=Р₂₉=8800 Н, Р₄=Р₅=Р₂₆=Р₂₇=2200 Н, жесткость рессоры EJ =12056 Н·м²; для положения 2 (рис. 4. в и г) Р₂=Р₂₉=10800 Н, Р₇=Р₂₄=6800 Н, Р₄=Р₅=Р₂₆=Р₂₇=2200 Н; для положения 3 (рис. 4. д и е) Р₂=Р₂₄=14080 Н, Р₇=Р₂₉=8000 Н, Р₄=Р₅=Р₂₆=Р₂₇=3520 Н или Р₂= Р₂₄=8000 Н, Р₇=Р₂₉=14080 Н, Р₄=Р₅=Р₂₆=Р₂₇=3520 Н; для положения 4 (рис. 4. ж и з) Р₂=Р₂₉=12800 Н, Р₇=Р₂₄=4800 Н, Р₄=Р₅=Р₂₆=Р₂₇=2200 Н.

Сопоставительный анализ результатов теоретических и экспериментальных исследований показал, что максимальные значения напряжения для дороги с гудронным покрытием удовлетворительного качества составляет соответственно 3% (рис. 4 а) и 3,2% (рис. 4 б), для дороги с гравийным покрытием с изношенными участками - соответственно 2,6% (рис. 4 в) и 9,3% (рис. 4 г), для поворотной полосы с грядами высотой 8-12 см и шагом 90 см - соответственно 8,2% (рис. 4 д) и 10,6% (рис. 4 е), для глубокого кювета глубиной 40-45 см и шириной 100-150 см - соответственно 7,4% (рис. 4 ж) и 8,5% (рис. 4 з).

Таким образом, предложенная методика расчета напряженно-деформируемого состояния рамы даёт хорошее согласование с экспериментальными данными (максимальные значения напряжения в пределах 11%) и ее можно использовать при обосновании прочностных параметров автотракторных прицепов.

 

Рис. 4 - Нормальные напряжения в узлах лонжерона при нагрузке 4 тонн:

а), в), д), ж) –при максимальных значениях растяжения волокон; б), г), е), з) – при максимальных значениях сжатия волокон; для а), б), в), г), д), е): 1, 2, 3 – экспериментальные значения, 4- расчетные значения; для ж), з): 1, 2- расчетные значения, 3 – экспериментальные значения

Литература

1. Проскуряков В.Б. Динамика и прочность рам и корпусов транспортных машин. – Л.: Машиностроение, 1972. – 232 с.
2. Maksimow V., Petukhow E., Jankovic D. Determination of semitrailers supporting units loading with pliancy elastic suspension brackets elements calculations // XV conference science and motor vehicles, 15 – 18 may 1995. – Beograd, 1995. – P.141 – 143.
3. Шермухамедов А.А., Усманов И.И., Салимджанов Р.Т., Тогаев А.А. Методы расчета и испытания автотракторных прицепов отечественного производства. Т., 2012.- 132 с.
4. Основы расчётов прочностной надёжности специальных элементов конструкций автомобилей и тракторов: учебное пособие / Г. В. Беликов. − Ульяновск : УлГТУ, 2007. − 98 с.
5. Феодосьев В.И. Сопротивление материалов: Учебник для втузов – 9-е изд., перераб. – М.: Наука. Гл. ред. физ.-мат. лит. 1986. – 512 с.
6. Еременко С.Ю. Методы конечных элементов в механике деформируемых тел. -Х.: Изд-во «Основа» при Харьковском университете, 1991. - 272 с.
7. Глущенко А.Д., Сливинский Е.В. Динамика и прочность транспортной системы для перевозки легковесных грузов. Ташкент: Фан, 1988.166 с.
8. Сливинский Е.В. Исследование колебаний и силового нагружения тракторного самосвального прицепа 2ПТС-4-793А. Автореф.дис.канд. техн.наук. Алма-ата. СХИ, 1977. 165 с.

References

1. Proskurjakov V.B. Dinamika i prochnost' ram i korpusov transportnyh mashin. – L.: Mashinostroenie, 1972. – 232 s.
2. Maksimow V., Petukhow E., Jankovic D. Determination of semitrailers supporting units loading with pliancy elastic suspension brackets elements calculations // XV conference science and motor vehicles, 15 – 18 may 1995. – Beograd, 1995. – P.141 – 143.
3. Shermukhamedov A.A., Usmanov I.I., Salimdzhanov R.T., Togaev A.A. Metody raschyota i ispytanija avtotraktornyh pricepov otechestvennogo proizvodstva. T., 2012.- 132 s.
4. Osnovy raschyotov prochnostnoj nadyozhnosti special'nyh elementov konstrukcij avtomobilej i traktorov: uchebnoe posobie / G. V. Belikov. − Ul'janovsk : UlGTU, 2007. − 98 s.
5. Feodos'ev V.I. Soprotivlenie materialov: Uchebnik dlja vtuzov – 9-е izd., pererab. – M.: Nauka. Gl. red. fiz.-mat. lit. 1986. – 512 s.
6. Eremenko S.Yu. Metody konichnyh elementov v mehanike deformiruemyh tel. -H.: Izd-vo "Osnova" pri Har'kovskom universitete, 1991. - 272 s.
7. Glushenko A.D., Slivinskij E.V. Dinamika i prochnost' transportnoj sistemy dlja perevozki lyogkovesnyh gruzov. Tashkent: Fan, 1988.166 s.
8. Slivinskij E.V. Issledovanie kolebanij i silovogo nagruzhenija traktornogo samosval'nogo pricepa 2PTS-4-793A. Avtoref.dis.kand. tehn.nauk. Alma-ata. SHI, 1977. 165 s.