МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РЕШЕНИЯ СТОХАСТИЧЕСКОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С РАВНОМЕРНО РАСПРЕДЕЛЕННЫМ СЛУЧАЙНЫМ КОЭФФИЦИЕНТОМ
Боровикова М.М.
Кандидат физико-математических наук,
Военный Учебно-Научный Центр Военно-Воздушных Сил “Военно-Воздушная Академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина” (Воронеж)
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РЕШЕНИЯ СТОХАСТИЧЕСКОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С РАВНОМЕРНО РАСПРЕДЕЛЕННЫМ СЛУЧАЙНЫМ КОЭФФИЦИЕНТОМ
Аннотация
В статье рассматривается начальная задача для дифференциального уравнения второго порядка со случайными коэффициентами. Решение этой задачи является случайным процессом. Получена формула для нахождения его математического ожидания в случае равномерного закона распределения случайного коэффициента.
Ключевые слова: математическое ожидание, уравнение со случайными коэффициентами, равномерное распределение.
Borovikova M.M.
PhD degree in Physics and Mathematics,
Air Force Military Training and Research Center “Air Force Academy named after Professor N.E. Zhukovsky and Yu.A. Gagarin” (Voronezh)
THE MATHEMATICAL EXPECTATION OF A SOLUTION OF THE STOCHASTIC DIFFERENTIAL EQUATION WITH UNIFORMLY DISTRIBUTED RANDOM COEFFICIENT
Abstract
The article considers an initial-value problem for the second-order differential equation with random coefficients. The solution of this problem is a stochastic process. Formula for the mathematical expectation of a solution is obtained for uniformly distributed random coefficient.
Keywords: mathematical expectation, equation with random coefficients, uniform distribution.
Постановка задачи
Рассмотрим начальную задачу для стохастического дифференциального уравнения второго порядка
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
где R – вещественная ось, ![]() – случайные величины,
– случайные величины, ![]() – случайный процесс. Тогда искомая функция
– случайный процесс. Тогда искомая функция ![]() также будет являться случайным процессом. Интерес представляет нахождение его статистических характеристик, в частности, математического ожидания.
также будет являться случайным процессом. Интерес представляет нахождение его статистических характеристик, в частности, математического ожидания.
Математическое ожидание решения будем искать в предположении, что ![]() независимы с
независимы с ![]() и в том смысле, что и
и в том смысле, что и ![]() , где – математическое ожидание, вычисленное по функции распределения случайного процесса z(t). Причём возможна зависимость
, где – математическое ожидание, вычисленное по функции распределения случайного процесса z(t). Причём возможна зависимость ![]() , а также
, а также ![]() .
.
Пусть ![]() заданы характеристическим функционалом [1]
заданы характеристическим функционалом [1]
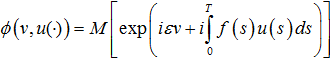
Здесь ![]() принадлежит пространству, сопряжённому к пространству реализаций процесса f(t).
принадлежит пространству, сопряжённому к пространству реализаций процесса f(t).
Сведение стохастической задачи к детерминированной
Введём вспомогательный функционал
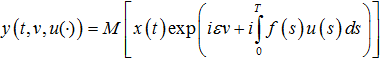
Заметим, что ![]() . Построим детерминированную задачу для нахождения y. Для этого умножим обе части равенств (1)-(3) на
. Построим детерминированную задачу для нахождения y. Для этого умножим обе части равенств (1)-(3) на 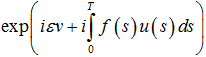 и вычислим среднее значение обеих частей
и вычислим среднее значение обеих частей
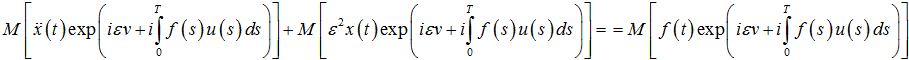 (4)
(4)
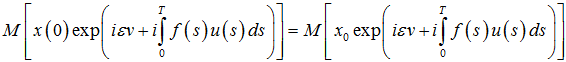 (5)
(5)
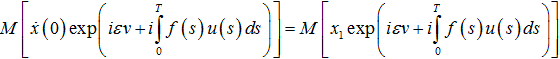 (6)
(6)
В терминах функционала y, с учетом независимости ![]() , соотношения (4), (5), (6) перепишутся в виде
, соотношения (4), (5), (6) перепишутся в виде
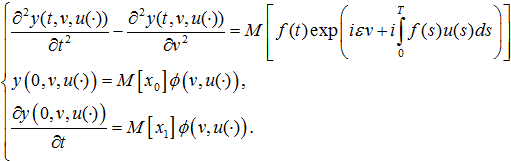
Так как нас интересует значение![]() , то, положив
, то, положив ![]() и для простоты записи обозначив
и для простоты записи обозначив ![]() , приходим к системе
, приходим к системе
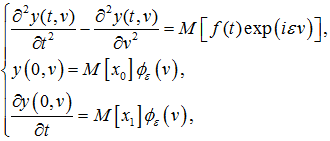 (7)
(7)
где ![]() – характеристическая функция случайной величины .
– характеристическая функция случайной величины .
Таким образом, задача нахождения математического ожидания решения исходного дифференциального уравнения со случайными коэффициентами была сведена к задаче с детерминированными коэффициентами, правда, вместо обыкновенного дифференциального уравнения, возникло уравнение в частных производных. Точное решение задачи (7) выписывается с помощью формулы Даламбера [2] и имеет вид
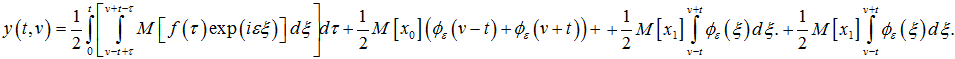
Полагая в последнем равенстве V=0, получим
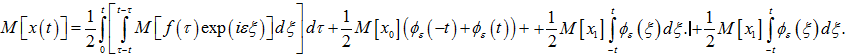 (8)
(8)
Формула (8) является достаточно общей, так как она применима для любых законов распределения случайных параметров задачи. Более того, рассмотренный метод позволяет получить формулы для моментных функций и более высокого порядка.
Математическое ожидание решения задачи (1)-(3) в случае независимости ![]()
Если случайная величина ε и случайный процесс f(t) независимы между собой, то ![]() , и формула (8) для вычисления математического ожидания решения задачи (1)–(3) примет вид
, и формула (8) для вычисления математического ожидания решения задачи (1)–(3) примет вид
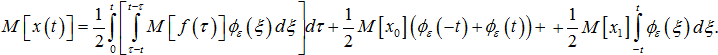
Поменяв порядок интегрирования в двойном интеграле, получим
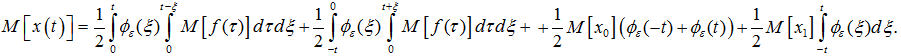 (9)
(9)
Математическое ожидание решения в случае стационарного случайного процесса f(t)
Пусть случайная величина ε независима со случайным процессом f(t) и, кроме того, f(t)– стационарный процесс, то есть ![]() – постоянная величина.
– постоянная величина.
В формуле (9) вынесем ![]() за знак интеграла и вычислим внутренний интеграл. Тогда
за знак интеграла и вычислим внутренний интеграл. Тогда
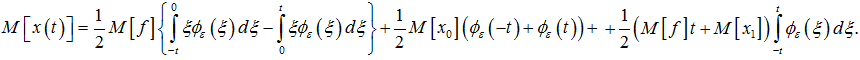 (10)
(10)
Далее, обозначим через ![]() . Вычислим
. Вычислим
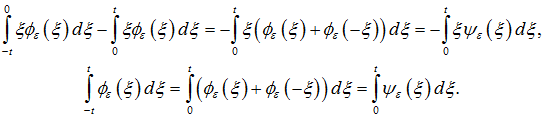
Подставив последние выражения в (10), получим
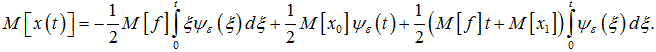 (11)
(11)
Заметим, что хотя для вывода формул для ![]() и требовалось знание функционала
и требовалось знание функционала ![]() , он в них не участвует, а в случае независимых
, он в них не участвует, а в случае независимых ![]() математическое ожидание решения исходной задачи полностью определяется средними значениями
математическое ожидание решения исходной задачи полностью определяется средними значениями ![]() и характеристической функцией случайной величины ε.
и характеристической функцией случайной величины ε.
Математическое ожидание решения в случае равномерного распределения
Пусть случайная величина ε имеет равномерное распределение со средним значением ![]() , тогда характеристическая функция имеет вид
, тогда характеристическая функция имеет вид 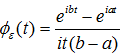 .
.
Преобразуем
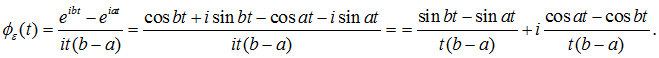
Вычислим 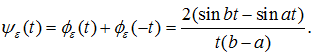
Подставляя полученное соотношение в (11), находим
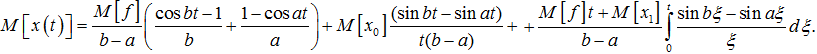 (12)
(12)
Итак, математическое ожидание решения задачи (1)-(3) в случае равномерно распределенной случайной величины вычисляется по формуле (12).
Хотелось бы отметить, что формула (11) позволяет найти математическое ожидание решения исходной задачи для любого распределения случайной величины , если известна ее характеристическая функция.
Литература
- Задорожний В.Г. Методы вариационного анализа / В.Г. Задорожний. – М. - Ижевск: НИЦ "Регулярная и хаотическая динамика", Институт компьютерных исследований, 2006. – 316 с.
- Тихонов А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. – М.: Изд-во МГУ, 1999. – 799 с.
References
- Zadorozhnij V.G. Metody variacionnogo analiza / V.G. Zadorozhnij. – M. - Izhevsk: NIC "Reguljarnaja i haoticheskaja dinamika", Institut komp'juternyh issledovanij, 2006. – 316 s.
- Tihonov A.N. Uravnenija matematicheskoj fiziki / A.N. Tihonov, A.A. Samarskij. – : Izd-vo MGU, 1999. – 799 s.
