ВОЗДЕЙСТВИЕ НЕЛИНЕЙНЫХ ПЛАНЕТАРНЫХ ВОЛН НА ОРИЕНТИРОВАННУЮ В ШИРОТНОМ НАПРАВЛЕНИИ СТЕНКУ
Перегудин С.И.1, Холодова С.Е.2
1Профессор, Санкт-Петербургский государственный университет; 2Доцент, Национальный исследовательский университет информационных технологий, механики и оптики
ВОЗДЕЙСТВИЕ НЕЛИНЕЙНЫХ ПЛАНЕТАРНЫХ ВОЛН НА ОРИЕНТИРОВАННУЮ В ШИРОТНОМ НАПРАВЛЕНИИ СТЕНКУ
Аннотация
В статье построена и математически реализована модель распространения нелинейных планетарных волн, а также их взаимодействие на ориентированную в широтном направлении стенку. Полученные решения позволяют произвести качественный анализ исследуемого динамического процесса, а также его численную реализацию.
Ключевые слова: гидродинамика, нелинейные волны.
Peregudin S.I.1, Kholodova S.E.2
1Professor, Saint Petersburg State University; 2Associate Professor, Saint Petersburg National Research University of Information Technologies, Mechanics and Optics
INFLUENCE OF NONLINEAR PLANETARY WAVES ON FOCUSED IN THE STENK WIDTH DIRECTION
Abstract
The article consideres model of distribution of nonlinear planetary waves, and also their interaction on the wall focused in the width direction is mathematically realized. The received decisions allow to get the qualitative analysis of studied dynamic process, and also its numerical realization.
Keywords: hydrodynamics, nonlinear waves.
Рассмотрим нелинейные течения и волны в тонком вращающемся с угловой скоростью ω слое идеальной несжимаемой жидкости между концентрическими полусферами.
Изучение нелинейных течений жидкости во вращающихся сферических слоях необходимо для понимания многих динамических процессов глобального масштаба в океане. В этом случае форма движения существенно зависит от двух важных факторов: сферической геометрии объема и вращения. Применение и необходимость такого рода исследований для проблем геофизики не вызывает сомнений [1].
Предполагая, что давление распределено по гидростатическому закону, основные уравнения движения теория мелкой воды [2] в сферической системе координат, связанной с вращающейся Землей, могут быть сведены к одному нелинейному уравнению с частными производными в терминах функции тока ![]() вида
вида
![]() (1)
(1)
Вертикальная проекция вихря скорости движения ξ с учетом соотношения (2) записывается в виде ![]()
Для слоя жидкости, находящегося между двумя концентрическими полусферами, функция глубины ![]() является константой и уравнение (1) запишется как
является константой и уравнение (1) запишется как
![]() (3)
(3)
где ![]() — сферическая функция порядка n; a — некоторая константа, определяющая угловую скорость зонального потока;
— сферическая функция порядка n; a — некоторая константа, определяющая угловую скорость зонального потока; ![]() — частота волны.
— частота волны.
Подставив выражение (4) в уравнение (3), получим соотношение для частоты волны ![]() :
:
![]() (5)
(5)
Таким образом, волна (4) представляет собой точное решение нелинейного уравнения (3) при выполнении соотношения для частоты волны (5).
Частота волны ![]() характеризует вращение волны относительно земной поверхности. Для перехода к линейной скорости
характеризует вращение волны относительно земной поверхности. Для перехода к линейной скорости ![]() движения волны на произвольной широте
движения волны на произвольной широте ![]() необходимо угловую скорость
необходимо угловую скорость ![]() умножить на радиус
умножить на радиус ![]() круга широты
круга широты
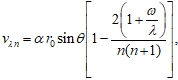 (6)
(6)
где ![]() — зональная скорость течения жидкости на широте
— зональная скорость течения жидкости на широте ![]() . Согласно формуле (6), волны, соответствующие малым значениям меридионального волнового числа n, а следовательно, и зонального числа m, поскольку суммирование распространяется на
. Согласно формуле (6), волны, соответствующие малым значениям меридионального волнового числа n, а следовательно, и зонального числа m, поскольку суммирование распространяется на ![]() распространяются с востока на запад. Для таких волн скорость
распространяются с востока на запад. Для таких волн скорость ![]() . Волны, соответствующие большим значениям m и n, распространяются с запада на восток. В этом случае
. Волны, соответствующие большим значениям m и n, распространяются с запада на восток. В этом случае ![]() . Решение (4) представляет собой волны, наложенные на западно-восточное течение, угловая скорость которого есть a. Аналогичное по виду решение содержится в работах Е.Н. Блиновой в задаче о волнах в атмосфере [3].
. Решение (4) представляет собой волны, наложенные на западно-восточное течение, угловая скорость которого есть a. Аналогичное по виду решение содержится в работах Е.Н. Блиновой в задаче о волнах в атмосфере [3].
В решении (4) в связи с учетом граничного условия ![]() полагается
полагается ![]() . Стационарное решение уравнения (3) определяется соотношением
. Стационарное решение уравнения (3) определяется соотношением ![]() . Это же соотношение может быть получено и другим способом, аналогичным тому, который использовал Йи Чиа-Шун [4].
. Это же соотношение может быть получено и другим способом, аналогичным тому, который использовал Йи Чиа-Шун [4].
В этом случае уравнения теории мелкой воды сводятся к уравнению
![]() (7)
(7)
где ![]() — функция Бернулли, зависящая только от ψ.
— функция Бернулли, зависящая только от ψ.
Изучение волновых движений, представляющих возмущения, распространяющиеся параллельно поверхности океана, позволяет ограничиться изучением двумерных движений жидкости, зависящих лишь от времени и угловых координат точки на поверхности сферической Земли. Обычно [2] для упрощения анализа принято рассматривать такие (планетарные) движения в ограниченной области поверхности сферы — в некоторой β‑ плоскости, в которой сфера локально заменяется плоскостью, но при этом учитывается изменение параметра Кориолиса в северном направлении.
Рассмотрим плоскопараллельное движение вращающейся несжимаемой жидкости, происходящее в β‑ плоскости, на которой введена система декартовых координат ![]() , так что ось
, так что ось ![]() направлена на восток, а
направлена на восток, а ![]() — на север. Эти движения описываются следующей системой уравнений:
— на север. Эти движения описываются следующей системой уравнений:
![]() (8)
(8)
![]() (9)
(9)
где ![]() — вектор скорости частиц жидкости,
— вектор скорости частиц жидкости, ![]() — параметр Кориолиса, зависящий от y, то есть, от широты места β‑ плоскости, причем вектор a перпендикулярен β‑ плоскости, p — динамическое давление, плотность жидкости для простоты записи предполагается равной единице. Уравнение (9) позволяет ввести функцию тока
— параметр Кориолиса, зависящий от y, то есть, от широты места β‑ плоскости, причем вектор a перпендикулярен β‑ плоскости, p — динамическое давление, плотность жидкости для простоты записи предполагается равной единице. Уравнение (9) позволяет ввести функцию тока ![]() :
:
Запишем уравнение (8) покомпонентно:
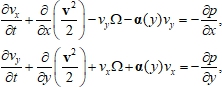
где ![]() . Дифференцируя первое по y, а второе по x, и вычитая одно из другого, получим
. Дифференцируя первое по y, а второе по x, и вычитая одно из другого, получим ![]() или в терминах функции тока
или в терминах функции тока ![]() или
или
![]() (10)
(10)
Здесь ![]() . Уравнение (10) запишем в виде
. Уравнение (10) запишем в виде
![]() (11)
(11)
Для бесконечно протяженной по горизонтали жидкости имеем точное решение нелинейного уравнения (11) ![]() . Параметр β будем считать постоянным.
. Параметр β будем считать постоянным.
Рассмотрим задачу об отражении нестационарных планетарных волн с конечной амплитудой от ориентированной в широтном направлении твердой стенки.
Пусть стенка расположена вдоль оси x. Условие непротекания в терминах функции тока ψ требует, чтобы
![]() (12)
(12)
Рассмотрим решение, соответствующее линейной суперпозиции падающей и отраженной волн:
![]()
Условие (12) на стенке ![]() принимает вид
принимает вид
![]()
Отсюда следуют равенства ![]() . Таким образом, предполагаемое решение примет вид
. Таким образом, предполагаемое решение примет вид ![]() являются корнями уравнения
являются корнями уравнения
Корни уравнения (13)![]() .
.
Линейная суперпозиция частных решений в виде набегающей и отраженной волн может не быть решением уравнения (11) для ψ. Поэтому подставим функцию ![]() в уравнение (11). Условием обращения в нуль левой части уравнения (11) для ψ будет равенство нулю произведения
в уравнение (11). Условием обращения в нуль левой части уравнения (11) для ψ будет равенство нулю произведения ![]() . При
. При ![]() .
.
Итак, решение соответствующего нелинейного уравнения представимо в виде линейной суперпозиции падающей и отраженной волн.
Литература
- Roesner K.G. Numerical calculation of hydrodynamic stability problems with time dependent boundary conditions // 6-я Международная конференция по численным методам в гидродинамике. Тбилиси. 1978.
- Педлоски Дж. Геофизическая гидродинамика. В 2-х т. М.: Мир, 1984. Т. 1. 400 с., Т. 2. 411 с.
- Блинова Е.Н. Гидродинамическая теория волн давления, температурных волн и центров действия атмосферы // Доклады АН СССР. – 1943. Т. 39.- № 7. – С. 284-287.
- Йи Чиа-Шун. Волновые движения в слоистых жидкостях // Нелинейные волны. – М.: Мир. 1977. – С. 271-296.
