СЛОЖНЫЕ КОЛЕБАНИЯ БАЛОК ЭЙЛЕРА-БЕРНУЛЛИ С УЧЁТОМ ГЕОМЕТРИЧЕСКОЙ И ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТЕЙ
Крысько В.А.1, Папкова И.В.2, Салтыкова О.А.3, Бабенкова Т.В.4, Кашубина А.А.5
1Доктор технических наук, профессор, 2кандидат физико-математических наук, доцент, 3кандидат физико-математических наук, доцент, 4кандидат технических наук, доцент, 5студент, Саратовский государственный технический университет имени Гагарина Ю.А.;
РФФИ Грант МОЛ
СЛОЖНЫЕ КОЛЕБАНИЯ БАЛОК ЭЙЛЕРА-БЕРНУЛЛИ С УЧЁТОМ ГЕОМЕТРИЧЕСКОЙ И ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТЕЙ
Аннотация
В данной работе рассматривается поведение неоднородной однослойной балки под действием знакопеременной нагрузки (давления), распределенной равномерно по всей ее поверхности. Исследование проводится с позиции качественной теории дифференциальных уравнений и нелинейной динамики. Построена теория нелинейной динамики балки с учетом физической геометрической нелинейности. Физическая нелинейность связана с учетом зависимости между деформацией и напряжением, а геометрическая нелинейность связана с зависимостью между деформацией и перемещением. Она принята в формуле Теодора фон Кармана. Теория построена на основе гипотезы Эйлера-Бернулли.
Ключевые слова: хаос, балка Эйлера-Бернулли, сходимость метода конечных разностей.
Krys'ko V.A.1, Papkova I.V.2, Saltykov O.A.3, Babenkova T.V.4, Kashubina A.A.5
1Dr. in Engineering, 2PhD physical and mathematical sciences, 3PhD physical and mathematical sciences, 4PhD physical and mathematical sciences, 5student Yuri Gagarin State Technical University of Saratov
COMPLEX OSCILLATION OF THE EULER-BERNOULLI BEAMS WITH REGARD GEOMETRICALLY AND PHYSICALLY NONLINEAR
Abstract
In this paper, we consider the behavior of the inhomogeneous single-layer beam under alternating load (pressure), distributed uniformly over its entire surface. The research is conducted from the perspective of the qualitative theory of differential equations and nonlinear dynamics. Construct a theory of nonlinear dynamics beams taking into account physical geometric nonlinearity. Physical nonlinearity associated with taking into account the relationship between strain and stress, and geometric nonlinearity associated with the relationship between the deformation and displacement. It accepted the formula of Theodore von Karman. The theory is based on the Euler- Bernoulli hypothesis.
Keywords : chaos, Euler-Bernoulli beam , the convergence of the finite difference method.
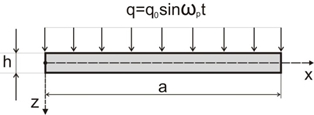
Постановка задачи В работе рассматриваются гибкие однослойные, тонкие балки, с длиной a и высотой h. Балка нагружается распределенной по ее поверхности нагрузкой- любое поперечное сечение, нормальное к серединной поверхности до деформации, остается после деформации прямым и нормальным к серединной поверхности, вместе с тем высота сечения не изменяется;
- инерция вращения элементов балки не учитывается, однако учитываются силы инерции, отвечающие за перемещения вдоль нормали к серединной поверхности;
- внешние силы не меняют своего направления при деформации балки;
- продольный размер балки значительно превышает ее поперечные размеры;
- геометрическая нелинейность учитывается в форме Т. Кармана [3].
Математическая модель балки описывается с учетом гипотезы Эйлера-Бернулли, нелинейной зависимости между деформациями и перемещениями и теории малых упруго-пластических деформаций. Материал, из которого изготовлены балки, считаем изотропным, но неоднородным, так что модули растяжения E, сдвига G, объемной деформации K, коэффициент поперечной деформации γ, предел текучести ![]() есть функции (x,z). Далее предполагается, что физические параметры материала E, G,K, v, т.е. модуль Юнга, сдвига, объемной деформации и коэффициент Пуассона соответственно являются однозначными функциями точки и деформированного состояния в ней. Деформированное состояние точки будем характеризовать объемной деформацией
есть функции (x,z). Далее предполагается, что физические параметры материала E, G,K, v, т.е. модуль Юнга, сдвига, объемной деформации и коэффициент Пуассона соответственно являются однозначными функциями точки и деформированного состояния в ней. Деформированное состояние точки будем характеризовать объемной деформацией ![]() и интенсивностью деформаций
и интенсивностью деформаций ![]() . Уравнения движения балки записываются в безразмерных параметрах (1):
. Уравнения движения балки записываются в безразмерных параметрах (1):
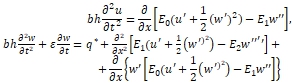 (1)
(1)
Граничные условия закрепления балки могут быть произвольными, но в данном случае рассмотрен вариант шарнирно-неподвижного опирания на концах:
![]() (2) Начальные условия имеют вид:
(2) Начальные условия имеют вид:
![]() {3)
{3)
где ![]() (i=0,1,2)
(i=0,1,2)
Здесь b - ширина балки, h - толщина балки, E - модуль упругости материала, (В дальнейшем при выводе уравнения движения балки мы предполагаем, что зависимость задана), t - время, ε – коэффициент демпфирования, w(x,t) – прогиб балки, u(x,t) – перемещения в срединной поверхности, q - усилие, действующее на балку, q0- амплитуда возникающей нагрузки, ωp - частота возникающей нагрузки.
Для учета физической нелинейности материала балок применяются деформационная теория пластичности и метод переменных параметров упругости [1]. Согласно этому методу модуль упругости и коэффициент Пуассона связаны с модулями сдвига и деформации следующими соотношениями:
Модуль K считается постоянным и равным ![]() . В деформационной теории модуль сдвига определяется по формуле
. В деформационной теории модуль сдвига определяется по формуле
![]() (5)
(5)
Диаграмма деформирования материала балок может иметь произвольный вид. В данной работе рассматривается идеально упруго –пластической материал:
![]() (6)
(6)
Интенсивность деформаций определяется выражением
![]() (7)
(7)
Составляющую ![]() находим из условия плоского напряженного состояния
находим из условия плоского напряженного состояния
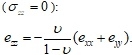
Если пренебречь составляющими ![]() для балки, то получаем
для балки, то получаем
![]() (8)
(8)
Закон изменения нагрузки во времени и вдоль оси балки может быть произвольным.
Система уравнений (1) сводится к системе обыкновенных дифференциальных уравнений методом конечных разностей, далее решается методом конечных разностей по времени. Шаг по времени выбирался по правилу Рунге.
Численный эксперимент
Рассматриваем прямолинейную балку с однородными граничными условиями (2) и нулевыми начальными условиями (3), находящейся под действием знакопеременной, равномерно распределенной нагрузки, заданной в виде ![]() , где
, где ![]() . Коэффициент диссипации
. Коэффициент диссипации ![]() . Целью работы является изучение характера колебаний балок в зависимости от количества деления отрезка в методе конечных разностей.
. Целью работы является изучение характера колебаний балок в зависимости от количества деления отрезка в методе конечных разностей.
Численный эксперимент показал, что при увеличении нагрузки q даже локальная частота хаотична (табл. 1). При q=10 ω1=10.6, при q=20 ω2=12.6, при q=25 ω3=19.4 и наблюдается повторное появление “всплеска” с частотой ![]() =28.7, q=30 ω4=20.2, а при q=35 происходят гармонические колебания, при этом ωp=20.7. Далее колебания опять становятся хаотичными и при q=50 ω5=27.2.
=28.7, q=30 ω4=20.2, а при q=35 происходят гармонические колебания, при этом ωp=20.7. Далее колебания опять становятся хаотичными и при q=50 ω5=27.2.
Таблица 1 – Спектр мощности при n=50, ω=20.7
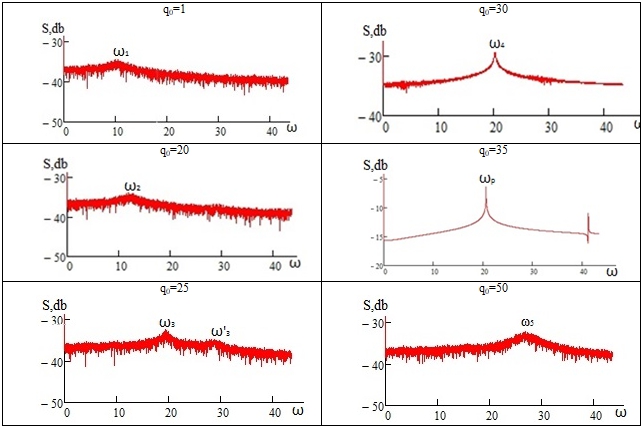
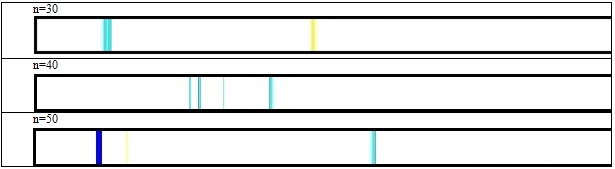
Рис. 2
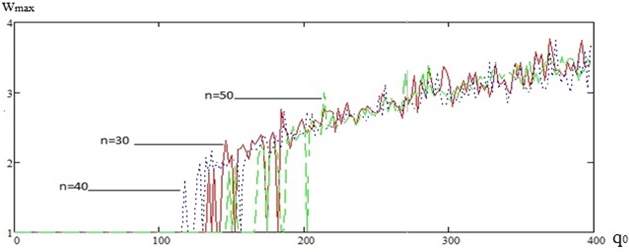
Рис. 3
В работе были построены шкалы (рис. 2) типа колебаний размером для управляющих параметров с использованием метода конечных разностей при количестве деления отрезка n = 30, 40, 50 для системы (1) – (3). Амплитуда внешнего воздействия менялась при этом на интервале (0;400), ![]() .
.
Идентификация типа колебаний при построении данных карт ![]() (рис. 3) для каждого сигнала
(рис. 3) для каждого сигнала ![]() проводилась с помощью анализа спектра мощности
проводилась с помощью анализа спектра мощности ![]() и показателей Ляпунова. Условные обозначения приведены под графиками. Полной сходимости в хаосе по максимальному прогибу не наблюдается. Система колеблется хаотически, начиная с очень маленькой нагрузки.
и показателей Ляпунова. Условные обозначения приведены под графиками. Полной сходимости в хаосе по максимальному прогибу не наблюдается. Система колеблется хаотически, начиная с очень маленькой нагрузки.
Литература
- Биргер И. А.Некоторые общие методы решения задач теории пластичности. ПММ, Т. 15, 1951, вып. 6.
- Вольмир А.С Нелинейная динамика пластин и оболочек. Москва: изд-ва «Наука», 1972 г. , 432 стр.
- Karman Th. Festigkeitsprobleme in Maschinebau // Encykle D. Math. Wiss. 1910. Vol. 4, №4, p.311-385.
