ОТРАЖЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ОТ СЛОИСТОЙ СТРУКТУРЫ СЕГНЕТОЭЛЕКТРИК-ФЕРРОМАГНЕТИК
Плугина Н.А.1, Риве В.В.2
1Студент, Магнитогорский государственный технический университет им. Н.Г. Носова; 2Кандидат физико-математических наук, Магнитогорский государственный технический университет им. Н.Г. Носова
ОТРАЖЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ОТ СЛОИСТОЙ СТРУКТУРЫ СЕГНЕТОЭЛЕКТРИК-ФЕРРОМАГНЕТИК
Аннотация
В статье исследована частотная зависимость коэффициента отражения электромагнитных волн от слоистой структуры сегнетоэлектрик-ферромагнетик.
Ключевые слова: слоистая структура, отражение волн от слоистой структуры, частотная зависимость коэффициента отражения.
Plugina N.A.1, Rivе V.V.2
1Student, Magnitogorsk State Technical University N.G. Nosov name; 2PhD in Physics and mathematics, Magnitogorsk State Technical University N.G. Nosov name
REFLECTION OF ELECTROMAGNETIC WAVES FROM THE LAYERED STRUCTURE OF FERROELECTRIC FERROMAGNET
Abstract
The paper studies the frequency dependence of the reflection coefficient of electromagnetic waves from a layered structure ferroelectric – ferromagnetic.
Keywords: the layer structure , reflection waves from the layered structure , the frequency dependence of the reflection coefficient.
В настоящее время слоистые структуры нашли широкое применение в различных областях. Моделирование процесса взаимодействия слоистой структуры с электромагнитным излучением позволит существенно сэкономить время и материалы на их изготовление, а также исследование свойств полученной структуры.
Количество слоев структуры может изменяться от одного до десятков и даже сотен. При большом количестве слоев структуры для их исследования широко используется метод матриц переноса [1], позволяющий рассчитывать коэффициенты поглощения, отражения и пропускания при относительно небольших затратах машинного времени при большом количестве слоев. В работах [4,5] показано, что у структур, содержащих ферромагнетики в зависимости от магнитной проницаемости может наблюдаться аномальное поведение коэффициентов отражения, в частности повышение практически до единицы или понижение до нуля в достаточно широком диапазоне частот.
Поведение коэффициентов зависит от геометрии структуры, а также диэлектрической и магнитной проницаемости материалов, образующих слои. Магнитная проницаемость в зависимости от частоты и температуры может изменяться в достаточно широком диапазоне. Аналогичным свойством обладает диэлектрическая проницаемость сегнетоэлектрика, исходя из этого, интересным является изучение расчет свойств слоистой структуры, содержащей сегнетоэлектрик в плане практического применения слоистых структур.
Рассмотрим периодическую структуру, состоящую из чередующихся n слоев ферромагнетика и сегнетоэлектрика, находящуюся в однородном внешнем магнитном поле, направленном по нормали к поверхности структуры, в вакууме, Для расчета предположим, что нечётный слой слоистой периодической структуры является изотропным ферродиэлектриком с проницаемостями ![]() , т.е. пренебрегаем гиротропией, а четный – сегнетоэлектрик с проницаемостями
, т.е. пренебрегаем гиротропией, а четный – сегнетоэлектрик с проницаемостями ![]() . Пусть из вакуума на первый слой структуры (ферромагнетик) падает перпендикулярно поверхности плоская монохроматическая электромагнитная волна TE поляризации с частотой ω. Геометрия задачи представлена на рис. 1. На данном рисунке светлые слои – ферромагнетик, темные - сегнетоэлектрик.
. Пусть из вакуума на первый слой структуры (ферромагнетик) падает перпендикулярно поверхности плоская монохроматическая электромагнитная волна TE поляризации с частотой ω. Геометрия задачи представлена на рис. 1. На данном рисунке светлые слои – ферромагнетик, темные - сегнетоэлектрик.
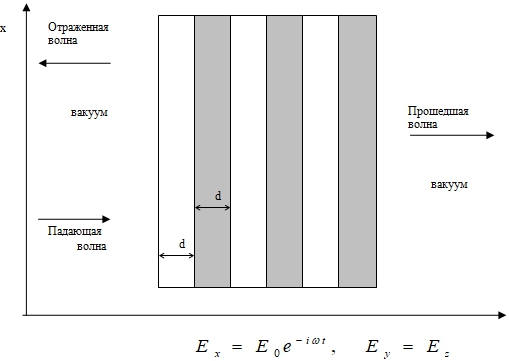
Рис. 1 - Геометрия задачи
Предположим, что толщина каждого слоя есть d, магнитная проницаемость ферродиэлектрического слоя имеет вид, типичный для кристалла кубической симметрии (при распространении волн вдоль оси типа [100]) [3,6]
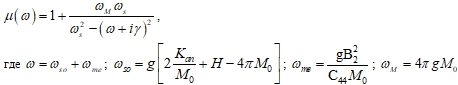
В приведенных формулах введены следующие обозначения: ![]() - частота магнитоакустического резонанса;
- частота магнитоакустического резонанса; ![]() - частота ферромагнитного резонанса;
- частота ферромагнитного резонанса; ![]() - частота магнитоупругой щели;
- частота магнитоупругой щели; ![]() - магнитостатическая частота; y - частота релаксации намагниченности; g - гиромагнитное отношение; M0 - намагниченность насыщения ферромагнитного слоя; H – напряженность внешнего магнитного поля;
- магнитостатическая частота; y - частота релаксации намагниченности; g - гиромагнитное отношение; M0 - намагниченность насыщения ферромагнитного слоя; H – напряженность внешнего магнитного поля; ![]() M0 - величина, характеризующая поле размагничивания; Kan - константа анизотропии; B2 - постоянная магнитоупругого взаимодействия; C44 - упругая постоянная;
M0 - величина, характеризующая поле размагничивания; Kan - константа анизотропии; B2 - постоянная магнитоупругого взаимодействия; C44 - упругая постоянная; ![]() – плазменная частота полупроводникового материала;
– плазменная частота полупроводникового материала; ![]() – частота столкновений электронов;
– частота столкновений электронов; ![]() – диэлектрическая проницаемость от связанных электронов.
– диэлектрическая проницаемость от связанных электронов.
Диэлектрическая проницаемость сегнетоэлектрического слоя также имеет вид, типичный для сегнетоэлектриков [2, 3,6]
![]()
Для расчета в сегнетоэлектрике значение магнитной проницаемости принято ![]() . Считаем, что падение электромагнитных волн нормальное, о есть угол падения равен нулю (
. Считаем, что падение электромагнитных волн нормальное, о есть угол падения равен нулю (![]() = 0). Тогда характеристическую матрицу ферромагнитного слоя можно записать в виде:
= 0). Тогда характеристическую матрицу ферромагнитного слоя можно записать в виде:
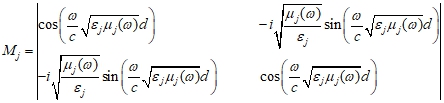
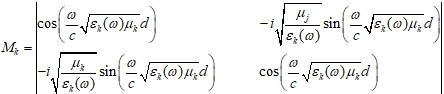
Зная характеристические матрицы слоев, можно записать матрицу переноса рассматриваемой слоистой структуры. Матрица переноса слоистой структуры равна произведению характеристических матриц отдельных слоев, при этом первым множителем будет матрица того слоя, на который падает электромагнитная волна.![]()
Энергетический коэффициент отражения в данном случае выражается следующим образом: ![]() .
.
В данной формуле ![]() , здесь i=0,1,
, здесь i=0,1, ![]() - диэлектрическая и магнитная проницаемости полубесконечной среды, ограничивающей структуру, из которой падает электромагнитная волна, θ1 - угол падения волны на слоистую структуру;
- диэлектрическая и магнитная проницаемости полубесконечной среды, ограничивающей структуру, из которой падает электромагнитная волна, θ1 - угол падения волны на слоистую структуру; ![]() - диэлектрическая и магнитная проницаемости полубесконечной среды, ограничивающей структуру, из которой выходит электромагнитная волна, θ2 - угол выхода волны из слоистой структуры. В рассматриваемом случае принимаем следующие значения параметров среды: ε1= μ1 = ε2 = μ2 = 1, θ1= θ2=0, р1 = р2=1.
- диэлектрическая и магнитная проницаемости полубесконечной среды, ограничивающей структуру, из которой выходит электромагнитная волна, θ2 - угол выхода волны из слоистой структуры. В рассматриваемом случае принимаем следующие значения параметров среды: ε1= μ1 = ε2 = μ2 = 1, θ1= θ2=0, р1 = р2=1.
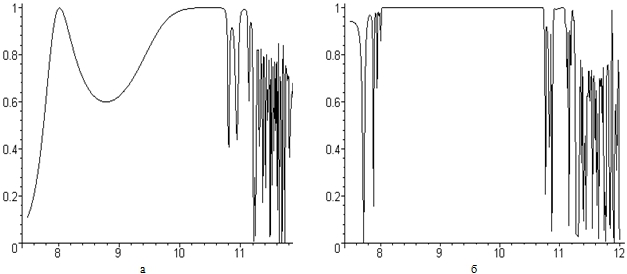
Рис. 2 - Частотная зависимость коэффициента отражения слоистой структуры
В случае небольшого числа слов наблюдается снижение коэффициента отражения в области ферромагнитного резонанса (рис. 2а). На рис. 2б количество слоев слоистой структуры увеличено до 70, расчет проводится в том же диапазоне частот и с теми же основными параметрами, которые указаны выше. С использованием приведенных расчетов распространения электромагнитной волны через слоистую структуру ферромагнетик – сегнетоэлектрик с помощью математического пакета Maple был разработан программный продукт, позволяющий получить частотную зависимость коэффициента отражения. Результаты работы программы представлены на рис. 2. Здесь по оси абсцисс откладывается lg(ω) по оси ординат – коэффициент отражения R. На рис. 2а представлены результаты расчета частотной зависимости коэффициента отражения слоистой структуры, состоящей из 5 слоев в диапазоне частот от 106 до 1012 . Численные значения величин взяты из работы [5, с. 96]: g=2´107 Э-1 с-1, M0=200 Э, eф =10, el =17,8; Kan =-105 эрг/см3, H =5000 Э, B2=107 эрг/см3, C44 =1012 эрг/см3. Параметры диэлектрической проницаемости сегнетоэлектрика (в данном случае рассматривается керамический материал BaTiO3 при температуре 200 С) ε0=178 и ε∞=18 получены из работы [2, с. 15], толщина слоя d = 0,2.
На представленных графиках наглядно видно, что при увеличении числа слоев в рассматриваемой структуре наблюдается полное отражение электромагнитных волн в достаточно широком диапазоне частот. Это позволяет найти практическое применение такой слоистой структуры.
Литература
- Борн М., Вольф Э. Основы оптики, пер. с англ. М.: Наука, 1973.- 360 с.
- Бегоян В.К. Физическое моделирование и исследование токов утечек ферроэлектрической керамической и пленочной структур: Автореф. дис. канд. техн. наук. – Ереван, 2012. – 25 с.
- Гуреев А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит, 1994. – 464 с.
- Риве В.В. Отражение электромагнитных волн от структур, содержащих магнитоупорядоченные среды: дис. канд. ф-м. наук. - Челябинск, 2007.
- Риве В.В. Отражение электромагнитных волн от структур, содержащих магнитоупорядоченные среды: Автореф. дис. канд. ф-м. наук. – Челябинск, 2007. – 23 с.
- Туров Е.А. Физические свойства магнитоупорядоченных кристаллов. Феноменологическая теория спиновых волн в ферромагнетиках, анти ферромагнетиках и слабых ферромагнетиках. М.: Изд-во АН СССР. - 1963. - 223 с.
