Использование генетических алгоритмов для решения оптимизационных задач природопользования
Использование генетических алгоритмов для решения оптимизационных задач природопользования
Аннотация
В работе приводятся результаты исследования возможности применения генетических алгоритмов для повышения эффективности финансовых вложений в природоохранные мероприятия. На основе балльных оценок экологического состояния основных природных сред и показателей, а также стоимости улучшения каждой составляющей разработан способ быстрого нахождения наилучшего варианта, который при минимизации затрат даёт максимальную отдачу. Освящены вопросы влияния размера начальной популяции хромосом на точность получаемого результата и количество требуемых итераций. Изучены вопросы применения генетических операторов скрещивания и мутации. Показано, что применение скрещивания с вероятностью 40% позволяет получить ответ, который в 4 и более раза точнее случая со 100% скрещиванием. Оператор мутации оправданно применять в редких случаях для больших по численности начальных популяций с вероятностью 0,001%. В результате поставленную задачу оптимизации получается решить до 81 раза быстрее.
1. Введение
Планомерное и постоянное развитие науки и техники позволяет учёным глубже и точнее исследовать биологический мир вокруг нас. Подобно тому, как искусственные нейронные сети были предложены после открытия их биологического источника, также генетические алгоритмы (ГА) являются попыткой воспроизвести некоторые естественные природные процессы.
Часть теоретических моделей и алгоритмов после открытия ожидают своей реализации и применения на протяжении десятков лет – до создания необходимых вычислительных мощностей и хранилищ данных. На сегодняшний день и процессоры компьютеров, и видеокарты обладают достаточным быстродействием для реализации и использования технологий искусственного интеллекта.
В связи с этим представляется актуальным применение генетических алгоритмов для решения оптимизационных задач в области рационального природопользования, где порой присутствуют значительные объёмы разрозненной первичной информации.
2. Объекты и методы исследования
Объектом исследования являются эколого-социальные системы, подверженные существенному антропогенному воздействию. Предмет исследования – повышение эффективности систем поддержки принятия решений для задач охраны окружающей среды с использованием генетических алгоритмов.
В общем виде можно сказать, что ГА – это правила нахождения экстремумов, базирующиеся на существующих в природе механизмах естественного отбора и наследования, использующие эволюционный закон выживания наиболее приспособленных особей.
Генетические алгоритмы относят к элементам искусственного интеллекта, которые копируют естественные природные механизмы, в соответствии с которыми выживание особи детерминировано степенью её приспособленности .
При этом от традиционных методов ГА отличаются рядом особенностей: имеют дело с закодированной формой, а не с исходными данными; в работе применяют только функцию приспособленности, без дополнительных данных; используют вероятностные правила отбора.
Вместе с тем, несмотря на широкий спектр сфер применения генетических алгоритмов не существует единых методов количественной оценки результативности и эффективности их использования. Поэтому авторы в научных статьях вынуждены самостоятельно искать подходы для сравнения и обоснования целесообразности применения тех, или иных технологий.
Так, например, авторы работы , исследуя существующие методы решения систем уравнений, описывают возможность ГА находить все имеющиеся ответы, и на основании этого делается вывод об их эффективности.
В статье ГА рассматриваются как результативный инструмент для оптимизации функции принадлежности лингвистических переменных в нечёткой системе наведения летательных аппаратов. Следуя научной логике, автор выполнил сравнение ближайших аналогов – метода пропорционального сближения и метода нечёткого пропорционального сближения с предложенным методом пропорционального сближения нечёткой оптимизации функции принадлежности. Полученные результаты позволяют утверждать о большей эффективности метода с применением ГА для решения частной рассматриваемой задачи.
Представляет интерес изложенный в работе подход, заключающийся в добавлении к классическому ГА дополнительных гибридных функций, заимствованных, у роевых алгоритмов. Изложенные результаты демонстрируют, что гибридные алгоритмы превосходят ГА как по точности результата, так и по скорости сходимости в задачах классификации ирисов Фишера. Так, например, на 30-й итерации ГА показал значение ошибки (разница между ожидаемым и получаемым результатом) на уровне 10, в то время как гибрид светлячков – 2. Допуская выигрыш в одном конкретном случае всё же стоит отметить, что гибридизация уменьшает универсальность ГА, и требует отдельного подбора «довесок» в каждом новом случае.
Задача оптимизации природоохранных мероприятий в чём-то схожа с рассматриваемой в работе проблемой оптимизации портфеля. Последняя при этом требует специфического предметного описания, что усложняет её решение ранее используемыми методами. Обосновывая применение ГА авторы не предлагают каких-либо количественных оценок и подходов к определению эффективности.
Проблеме использования ГА в области информационного поиска посвящена работа . Разработанный авторами алгоритм был протестирован на базе данных Cranfield, изложенные результаты признаны перспективными, а для получения новых данных показана необходимость в проведении дальнейших исследований.
Завершим краткий обор работой , где авторы делятся результатами применения ГА для решения транспортной задачи. Сопоставляя работу ГА с алгоритмом имитированного отжига показано влияние качества начальной популяции на производительность алгоритма. Результаты подтверждают, что наличие лучших особей в начальной популяции положительно влияет как на лучшее решение, так и на среднее решение генетического алгоритма. Вместе с тем в статье отсутствуют однозначные выводы по эффективности ГА. На задачах по построению оптимального маршрута по заданным маршрутам наиболее эффективным с точки зрения быстродействия и точности оказался генетический алгоритм, в то время как на задачах с меньшим количеством точек и итераций лучшие результаты показал муравьиный алгоритм .
Как видно из приведённых выше исследований ГА могут применяться для нахождения решений в различных прикладных задачах, при этом их эффективность повышается с увеличением пространства поиска.
Предложенный алгоритм интегральной оценки качества окружающей среды урбанизированных территорий позволяет сформировать по результатам натурных исследований и последующей обработке сопоставимые балльные оценки для семи экологических показателей для каждой зоны, отличающейся своим ландшафтом, состоянием и сферой использования. При этом стоимость природоохранных мероприятий для улучшения на один балл экологического состояния как по различным показателям, так и для разных территорий будет отличаться. Отметим также, что выбор самих мероприятий также может быть автоматизирован с учётом, например, влияния качества окружающей среды на здоровье населения, с использованием элементов искусственного интеллекта , .
Постановка задачи: разработка метода выбора оптимального вложения финансовых средств в природоохранные мероприятия с использованием генетических алгоритмов.
Исходя из единой пятибалльной шкалы оценки всех компонентов, изменение в меньшую сторону на DО является равно благоприятным для улучшения экологического состояния всех анализируемых сред. Непосредственно стоимость изменения, выраженная в рублях, может рассчитываться по аналогии с уже реализованными мероприятиями, или устанавливаться экспертами.
После определения принципов кодирования исходных данных поставленная задача оптимизации может быть решена при помощи классического генетического алгоритма, состоящего из шести пунктов:
1. На первом шаге генерируется популяция особей в количестве 8 путём либо полного случайного составления, либо с учётом одной «удачной» хромосомы, отобранной на предыдущих шагах.
2. Происходит расчёт Fitness-функции (приспособленности) по всей популяции. На основании её значения выбираем лучшую хромосому, нумеруем её как 8 и записываем в новый набор.
3. Недостающие 7 хромосом получаем в ходе турнирной селекции, когда сформированные случайным образом пары конкурируют между собой.
4. Проводим скрещивание хромосом.
5. Проверяем условие продолжения работы алгоритма, и при выявлении признаков сходимости возвращаемся к п. 1.
6. Переход к п.2.
На практике данный генетический алгоритм выглядит следующим образом.
Для формирования ландшафта поиска необходимо иметь числовые ряды (Кj1,Оj1; … Кj7Оj7), где j – порядковый номер участка исследуемой территории; Кj1 - Кj7 – показатели балльной оценки воздуха, почвы, водных ресурсов, лесных насаждений, уровня шума и вибраций, электромагнитных излучений и объёмов накопления отходов; Оj1- Оj7 – стоимость в рублях изменения в лучшую сторону балльной оценки (на 1 балл) для перечисленных показателей.
Математическую модель задачи можно представить в виде:
при ограничениях: КjiÎ[0..5]; Оji > 0; Оji ≤ S,
где М – количество подрайонов;
N – количество учитываемых показателей.
S – объём выделенных средств, руб.
Очевидно, что для решения описанной задачи именно стоимость затрат на природоохранные мероприятия будет выступать в качестве функции приспособленности.
Далее промоделируем выполнение алгоритма для условного числа зон, равного 256:

Рисунок 1 - Начальная популяция
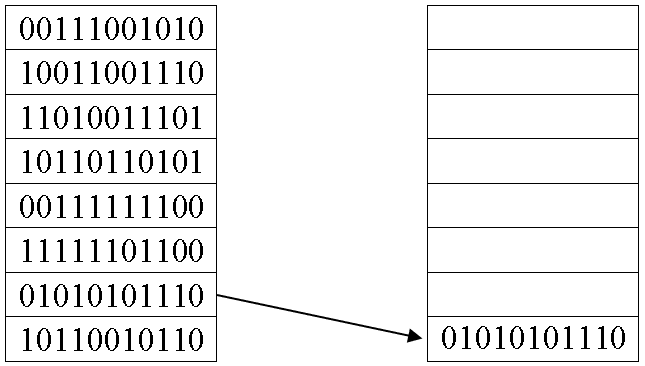
Рисунок 2 - Результат отбора лучшей хромосомы
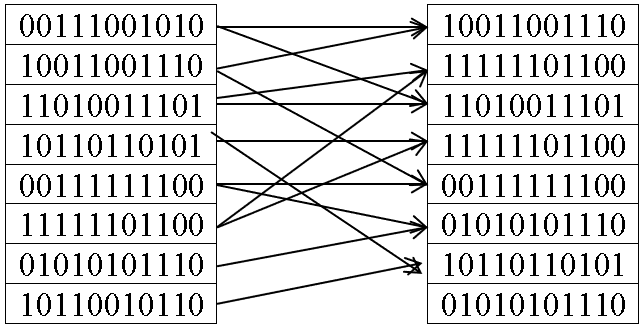
Рисунок 3 - Результат турнирной селекции хромосом
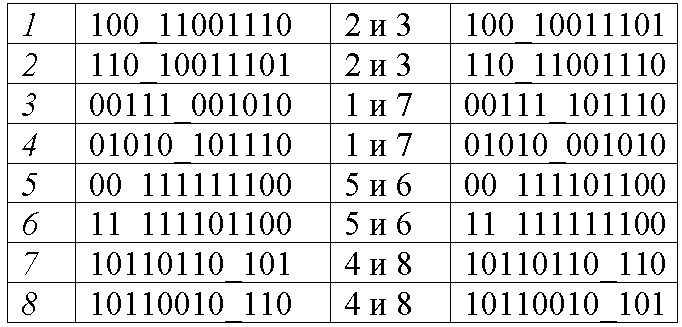
Рисунок 4 - Результат выполнения операции скрещивания
6. Продолжить работу алгоритма – перейти к пункту 2.
Тут важно заметить, что алгоритм в результате своей работы найдёт одну наиболее подходящую для вложения средств зону с указанием на конкретный параметр – экстремум. Если разница между S и Оji достаточная, то данная альтернатива помечается и алгоритм может быть запущен ещё раз.
Необходимое число бит в двоичной системе для формирования хромосомы в контексте описываемой задачи определяется кодированием количества подрайонов и экологических показателей, при этом в процессе работы алгоритма требуется отслеживать случаи вырождения трёх правых ген.
После выполнения описанного алгоритма несколько раз будет получен план вложения финансов в природоохранные мероприятия по конкретным зонам и природным средам, или другими словами – будет решена оптимизационная задача. Количество запусков алгоритма зависит от объёма финансирования, подлежащего распределению.
Проведение моделирования решения описанной задачи для различных исходных данных показало, что ГА находит приемлемое решение в среднем за 5 повторов. С целью получения усреднённых оценок результативности алгоритм выполнялся 10 000 раз с использованием случайного набора исходных данных. В таблице 1 представлены полученные результаты.
Таблица 1 - Полученные при моделировании результаты
Число запусков ГА | 5 | 30 | 50 | 100 | 150 | 250 | 350 | 650 | 1000 | 2000 | 3000 | 7500 | 10000 |
Суммарное количество повторений | 22 | 174 | 273 | 571 | 855 | 1405 | 2070 | 3757 | 5732 | 11329 | 16862 | 40650 | 56325 |
Среднее количество итераций для нахождения решения
| 4,40 | 5,80 | 5,46 | 5,71 | 5,70 | 5,62 | 5,92 | 5,78 | 5,73 | 5,66 | 5,62 | 5,42 | 5,63 |
Как следует из данных таблицы 1, при увеличении количества запусков ГА среднее количество итераций, за которое алгоритм находит решение, сходится к 5,7. В единичных случаях результат может быть получен и ранее.
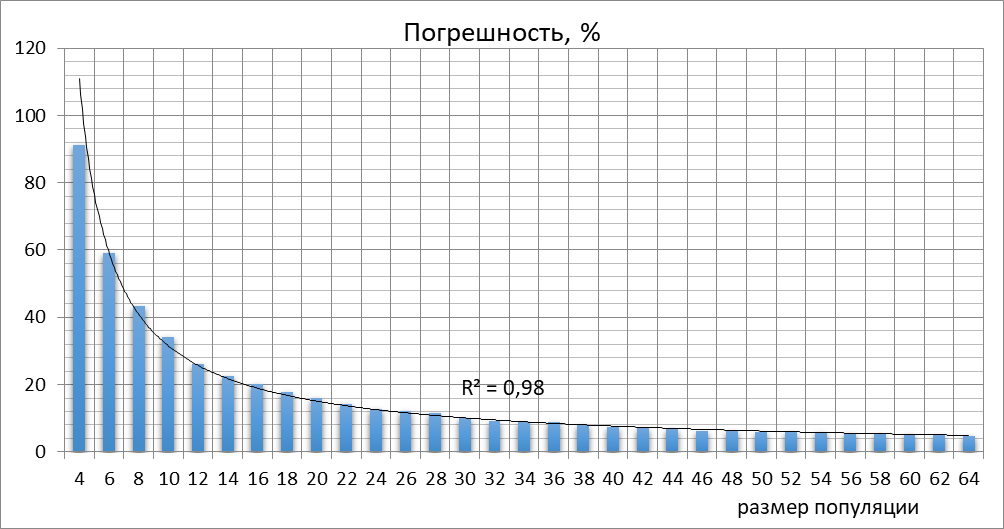
Рисунок 5 - График изменения точности при росте количества хромосом в популяции
Чтобы выполнить оценку эффективности применения ГА для решения оптимизационных задач на обширном ландшафте поиска, проанализируем данные, получаемые, например, из программы МетаТрейдер, которая для подбора оптимальных параметров использует рассматриваемые инструменты.
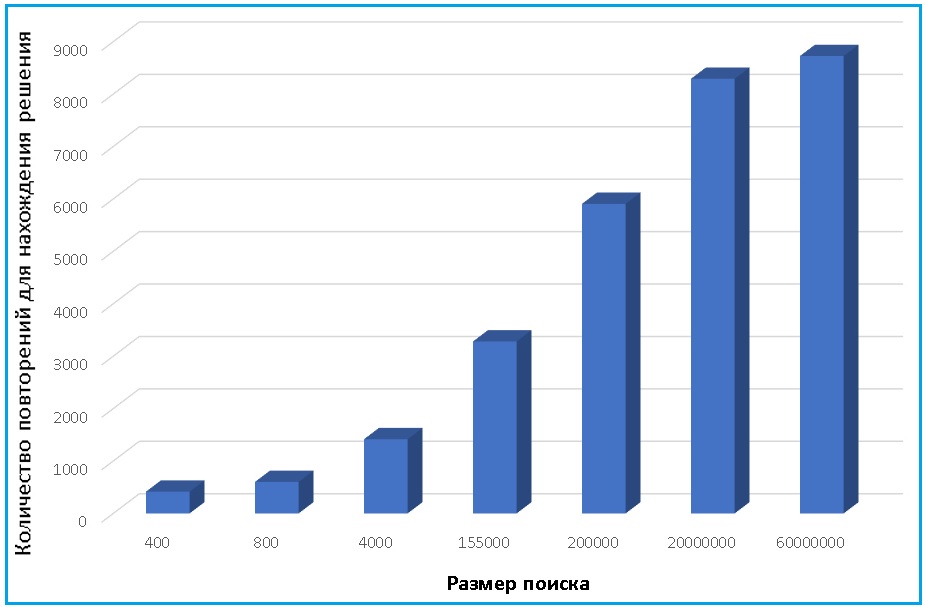
Рисунок 6 - Зависимость количества повторений для нахождения решения от начального размера поиска
Изложенные до этого момента результаты были получены при работе ГА с вероятностью скрещивания равной 100 %.
Таблица 2 - Влияние вероятности скрещивания на показатель точности результата
Вероятность осуществления скрещивания, % | 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 |
Среднее количество итераций до получения решения | 26,2 | 23,5 | 23,1 | 22,4 | 23,1 | 20,3 | 21,4 | 23,5 | 24,6 | 27,9 | 57,8 |
Уровень погрешности, % | 2,7 | 3,1 | 1,8 | 1,13 | 0,73 | 0,71 | 0,62 | 0,84 | 1,16 | 1,53 | 2,67 |
Как следует из таблицы 2, наименьшие значения погрешности достигаются при вероятности скрещивания в диапазоне от 40 до 50%. При этом также важно заметить, что точность работы ГА влияет на его сходимость – при указанных показателях среднее количество повторений, за которое ГА находит экстремум, минимально и составляет 20-21.
Из научной литературы следует, что генетический оператор мутации используется реже оператора скрещивания в тысячи раз и служит для привнесения в популяцию «свежих идей извне». Его применение, реализуемое инвертированием случайного гена, показало, что при вероятности более одного процента сходимость ГА полностью нарушается. При значениях 0,5 % получаемый результат всё ещё хуже как по количеству требуемых итераций, так и по уровню погрешности. Дальнейшее уменьшение вероятности оператора мутации показало, что при величине 0,05 % количество шагов ГА несущественно уменьшается при одинаковых уровнях погрешности. В описанной задаче оптимизации финансовых вложений обоснованным уровнем вероятности мутации явились значения в диапазоне от 0,01 до 0,001 %. Вместе с тем очевидно, что для указанных величин размер популяции должен быть 10000 и 100000 хромосом соответственно.
3. Результаты и обсуждения
Выполненные исследования позволяют утверждать о высокой эффективности применения генетических алгоритмов для решения оптимизационных задач в области природоохранных мероприятий. Найденные параметры размера начальной популяции, вероятностей генетических операторов скрещивания и мутации позволяют приблизить точность получаемого результата к абсолютному (а не локальному) экстремуму.
Хотя, как было показано выше, не существует единой методики численной оценки эффективности ГА, для решаемой задачи предлагается отталкиваться от количества сравнений, необходимых для нахождения минимума на всём ландшафте поиска. Таким образом, для изложенного примера с количеством подрайонов равным 256, необходимо оперировать семью значениями, выражающими стоимость природоохранных мероприятий, которые требуются для изменения оценки на один балл для каждого из представленных экологического показателя. Для поиска минимального значения в массиве из 1792 элементов (256*7) требуется в худшем случае 1792 итерации (в зависимости от расположения элемента). При этом описанный ГА, использующий оператор скрещивания с вероятностью 100%, находит решение в среднем за 28 итераций с погрешностью менее 4% при размере популяции равном 100. Для достижения погрешности менее 1 % в среднем требуется 95 итераций на размере в 500 хромосом.
Если использовать модифицированный ГА с вероятностью скрещивания на уровне 40% решение находится за 22 итерации с погрешностью 0,6%. Такой результат в 81 раз быстрее прочих алгоритмов нахождения экстремумов.
4. Заключение
Как показали проведённые исследования и полученные результаты генетические алгоритмы являются результативным методов решения оптимизационных задач. При этом с возрастанием объема исходных данных эффективность ГА повышается параболически.
Для решения задачи оптимизации природоохранных мероприятий предложено использовать кодовое представление номеров исследуемых подрайонов и экологических показателей. При этом в результате работы ГА определяется перечень зон, для которых финансирование приведёт к наибольшему эффекту при минимальных вложениях.
По сравнению с классическими методами поиска экстремума ГА способны до 81 раза быстрее получать результат при достаточно приемлемом уровне погрешности 0,6 %. При этом необходимо отметить, что в ряде случаев от скорости принятия адекватных управленческих решений зависит функционирование целого города, или региона, например, в случае природных, или техногенных чрезвычайных ситуаций. Поэтому применение ГА не ограничивается обозначенной в данной работе областью.
