ИССЛЕДОВАНИЕ ЭНЕРГОЗАТРАТ НА ВЗЛЕТ КВАНТОМОБИЛЯ
ИССЛЕДОВАНИЕ ЭНЕРГОЗАТРАТ НА ВЗЛЕТ КВАНТОМОБИЛЯ
Аннотация
Перспектива внедрения квантомобилей, использующих тягу (траст) квантового двигателя-движителя (КДД), реализуемую в плоскости тангажа, приводит к необходимости рассмотрения особенностей формирования энергозатрат на взлет этих машин. Механизмы формирования энергозатрат на работу сил, коллинеарных продольному движению экипажа, и работу вертикальных сил, обеспечивающих висение экипажа, существенно различаются. В отсутствие натурных транспортных средств (ТС) с КДД ставка в исследовании делается на программное имитационное моделирование (ПИМ), гибкую модель и мощное ПО. Проблема заключается в формировании структуры анализа энергозатрат на реализацию взлета квантомобиля. Задачами разработки явились: формирование алгоритмов анализа энергозатрат квантомобиля; создание в авторской Модели приземного движения квантомобиля (МПДК) Подсистемы расчета энергозатрат (ПРЭ); отработка интерфейса взаимодействия с моделью; проведение ПИМ на базе МПДК с экспериментами, охватывающими некоторое множество вариантов взлета ТС. Методы. Развитие авторского алгоритма взлета и висения квантомобиля, реализованного в среде Simulink-модели МПДК. Формирование на базе ПИМ процессов взлета квантомобиля траекторного каркаса множества взлетов. Оценка энергоэффективности реализаций взлета с привлечением алгоритмических и графических возможностей ПО Matlab. В серии расчетов разгонов и вывешивания квантомобиля при различных сценариях изменения углов наклона вектора траста, сопротивления воздуха и подъемной силы, сопротивления качению по опорной поверхности и других факторов дана оценка энергозатрат для вариантов взлета квантомобиля. Заключение. Разработанная в среде МПДК подсистема ПРЭ позволяет проводить расчетное исследование энергозатрат как на преодоление продольных сил сопротивления движению, так и на вертикальное вывешивание экипажа с обеспечением его устойчивости в плоскости тангажа. На базе проведенных посредством МПДК с ПРЭ расчетов и их анализа преодолена познавательная сложность формирования энергозатрат квантомобиля на стадии его взлета с расщеплением их по видам сил сопротивления движению. МПДК рассматривается в качестве основы для дальнейшего развития моделирования движения квантомобиля в произвольных условиях.
1. Введение
На базе идей извлечения энергии из физического вакуума (ФВ) , , в физике рассматриваются концепции квантовых двигателей (КД), генерирующих траст (тягу) за счет целенаправленной деформации поля ФВ , . Примером могут служить разработки Леонова В.С. , . Надежда на практическую реализацию названых идей и концепций становится все более существенной , .
Реализация идеи КД приведет к появлению нового типа транспортных средств (ТС) – квантомобилей , , . Станет возможным прикладывать траст КД к корпусу экипажа непосредственно – без трансмиссии. Необходимость трансмиссии отпадет, колесам (при движении по опорной поверхности (ОП)) останется только опорная функция , .
При шарнирном обметании вектора траста в плоскости тангажа проявляется его вертикальная компонента, которую можно использовать для вертикального вывешивания – лифта квантомобиля (в роли трастовой подъемной силы – ТПС). Горизонтальная компонента траста при этом используется для преодоления сил сопротивления продольному движению экипажа , (здесь и везде далее используем слово «экипаж» в смысле «коляска», но не команда!). КД, с реализацией таким образом функций движителя ТС, становится силовой установкой типа Квантовый двигатель-движитель (КДД).
В рамках продольного движения квантомобиля в плоскости развёртывания угла тангажа β вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz , :
В скалярной записи это:
В публикациях , , на базе авторской Модели приземного движения квантомобиля (МПДК) рассмотрена методика и даны примеры расчета тяговых сил квантомобилей для наземной среды движения ТС с возможным переходом в воздушную среду. Показывается, что расчетная методика, в связи с необходимостью учета лифта, отличается от традиционных алгоритмов расчета силового баланса автомобиля.
В работах , автором рассматривались вопросы продольной устойчивости квантомобиля.
В работах , обосновывались те требования к энергетической цене тяги (ЭЦТ) КДД, которые позволят квантомобилю превосходить современные ТС-аналоги по энергоэффективности. При этом было обусловлено разделение ЭЦТ на энергетическую цену горизонтальной тяги (ЭЦГТ) и энергетическую цену вертикальной тяги (ЭЦВТ).
Было отмечено, что размерность ЭЦТ, ЭЦГТ и ЭЦВТ: [Вт/Н] = [м/с] – суть размерность скорости. Именно с этой скоростью (что очевидно для горизонтального перемещения) энергия передается от мобильного объекта в среду движения . Это обуславливает простоту вычисления мгновенной мощности процесса горизонтального перемещения экипажа (произведение силы на скорость коллинеарного движения) и затем – работы и энергозатрат (интегрированием мощности по времени).
Для вертикального движения, особенно для вывешивания экипажа, всё не так просто – экипаж неподвижен, а энергия на висение затрачивается. В статье сформирована методика выработки требований к величине ЭЦВТ КД квантомобиля. Показано, что, например, для 10-тонного квантомобиля-грузовика ЭЦВТ должна быть менее 55 Вт/Н.
Взлёт объекта становится возможным только тогда, когда суммарная подъемная сила (СПС) (сумма аэродинамической и трастовой подъемных сил (АПС и ТПС)), превосходит вес этого объекта.
В статье показано, что с внедрением КДД в конструкцию ТС становится возможным моделирование взлета экипажа по единому алгоритму, охватывающему непрерывным образом все существующие способы (варианты) взлета ТС (от «самолетного» до «вертолетного»): CTOL, STOL и VTOL . Объединяющим фактором синтеза способов взлета в алгоритме является наличие у квантомобиля ТПС.
В работе также оценена динамика процессов, учет упругих сил и демпфирования в подвеске экипажа при взлете – это тоже сопровождается энергозатратами.
Затронутые аспекты, несомненно, должны найти место в анализе энергозатрат квантомобиля. Гипотезой исследования может быть следующее утверждение: при исследовании энергозатрат на взлет квантомобиля возможно расщепленное представление этих затрат по видам продольных и вертикальных составляющих траста и сил воздействия среды движения на экипаж – со сведением компонентных энергозатрат в их скалярную сумму.
2. Методы и принципы исследования
2.1. Цель и задачи исследования
Целью исследования явилось формирование структуры анализа энергозатрат на реализацию взлета квантомобиля.
Отсутствие признанных теоретических основ движения квантомобиля, натурных образцов исследуемых объектов и эмпирических данных по ним, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются:
1) формирование математической модели движения квантомобиля под поставленную цель;
2) разработка в авторской Simulink-модели приземного движения квантомобиля (МПДК) Подсистемы расчета энергозатрат (ПРЭ), позволяющей проведение исследования энергозатрат на различных фрагментах движения квантомобиля с детализацией составляющих по видам воздействия на экипаж в плоскости тангажа;
3) отработка интерфейса взаимодействия с моделью, задания сценариев взлета, контроль движения экипажа, многофакторного вывода результатов;
4) проведение ПИМ на базе Simulink-модели с экспериментами, охватывающими некоторое множество вариантов взлета ТС с оценкой компонентных и общих (суммарных) энергозатрат;
5) обсуждение и обобщение результатов расчетов;
6) формирование рекомендаций и выводов.
2.2. Балансы сил и моментов в 3-DOF модели приземного движения квантомобиля
Используем 3-DOF модель приземного движения квантомобиля (МПДК), развиваемую в авторских работах , , – учитываем балансы горизонтальных сил, вертикальных сил и моментов сил, действующих в плоскости тангажа.
Баланс горизонтальных сил, действующих на квантомобиль , :
где Fr – сила сопротивления качению опорных колес, Н;
Fwx – сила сопротивления воздуха продольному движению, Н;
Fax – продольная сила инерции экипажа, Н;
Gq' – сила давления экипажа на ОП с учетом частичного лифта, Н;
fk0 – коэффициент сопротивления качению колес при нулевой скорости;
fkv – скоростной коэффициент сопротивления качению колес, с2/м2;
Vq – скорость продольного движения квантомобиля, м/с;
cd – коэффициент продольного аэродинамического сопротивления;
ρw – плотность воздуха, Н ×с2/м4;
Sfr – фронтальная (лобовая) площадь экипажа, м2;
Gq – сила тяжести квантомобиля (Gq = m·g), Н;
g – ускорение свободного падения, м/с2;
ax – продольное ускорение экипажа, м/с2;
δwh – коэффициент инерции вращения опорных колес экипажа.
Сила Gq' = Gq – (FTz+Fwz) = Gq – FzSum, где Fwz – АПС, а FzSum – СПС. Для квантомобиля приведенная масса m’ = Gq(1+δwh)/g учитывает вращение только опорных колес (привод отсутствует).
Баланс вертикальных сил :
где Fup(z) – сила упругости подвески (меняющаяся по вертикальному ходу z);
Fам(vz) – сила сопротивления амортизаторов подвески (зависящая от скорости вертикального движения vz);
Fvpl(vz2) – сила воздушного сопротивления вертикальному движению экипажа (с учетом его площади в плане Spl);
Faz(az) – сила инерции, возникающая при вертикальном ускорении az.
С учетом того, что Fup(z) = Gq – z·cup, (где cup – приведенный коэффициент упругости (жесткости) подвески), можно записать:
Обозначив z·cup = Fpz и заметив, что это – высвободившаяся часть силы упругости, перешедшая в потенциал лифта, можем записать для силы, идущей на вертикальное ускорение экипажа:
где Fvz = Fам(vz) + Fvpl(vz2) – совокупность сил, связанных со скоростью вертикального движения экипажа.
В форме ДУ это:
где: kam – приведенный коэффициент демпфирования амортизаторов подвески, Н·с/м;
kwv = cdv ·(ρw/2)·Spl – фактор вертикальной обтекаемости экипажа, Нс2м–2;
cdv – аэродинамический коэффициент сопротивления вертикальному перемещению экипажа;
Spl – площадь в плане экипажа, м2.
Детали и особенности использования баланса вертикальных сил в МПДК можно почерпнуть из работы . Упомянем только, что система вертикальных перемещений экипажа учитывает три этапа: этап I с опорой на колеса (до высоты Hlf1) (конфигурация 1); этап II движения вывешенного над ОП экипажа с висящей подвеской (до высоты Hlf2) (все еще конфигурация 1), за ним этап III – с убранной подвеской и выдвинутым оперением (до высоты Hlf3) (конфигурация 2).
Баланс моментов сил усовершенствован на базе схемы рис. 1 (с профилем Davis), где обозначены: Vq – вектор скорости движения квантомобиля; V∞ – скорость невозмущенного набегающего потока воздуха (|V| = |V∞|); Cg – центр тяжести (ЦТ) экипажа; Gq – сила тяжести экипажа; Fa – приведенная сила инерции экипажа; CFT – точка приложения траста КД к корпусу экипажа; FT, FTx и FTz – сила тяги КД (траст) и ее покоординатные компоненты; Cw – центр давления (ЦД) аэродинамических сил; Fw, Fwx и Fwz – сила воздействия воздуха и ее покоординатные компоненты; Ff1 и Ff2 – силы сопротивления качению передних и задних колес, соответственно; Tf1 и Tf2 – моменты сопротивления качению колес; hFwx, hFTx, hg – расстояния векторов соответствующих сил Fwx, FTx, Fa от ОП; lFwz, lFTz – расстояния векторов соответствующих сил Fwz, FTz до вертикали от оси задних колес; l0 – расстояние вектора силы Fwz до вертикали центра колесной базы; Lwb, L1 и L2 – расстояния базовое и от осей колес до проекции центра тяжести на ОП; A и B – центральные точки пятен контакта колес с ОП; Rz1 и Rz2 – нормальные реакции ОП; Lst – расстояние между стабилизирующими трастерами (введено в настоящем исследовании).
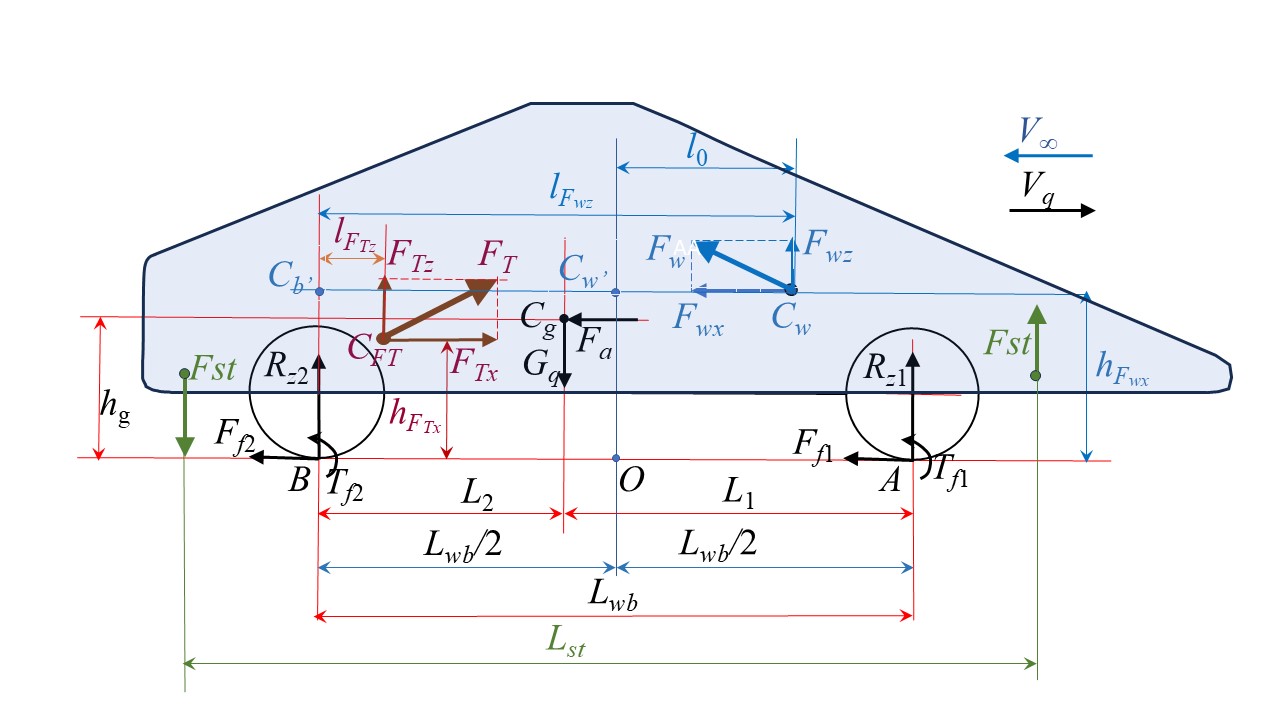
Рисунок 1 - Схема сил, формирующих балансы сил и моментов
Из него можно найти нормальную реакцию ОП Rz1. Аналогичное уравнение моментов относительно точки A позволяет найти реакцию Rz2. Опрокидывающий питч-момент MΣpm = Lwb(Rz1–Rz2)/2. Требуемый стабилизирующий момент (ТСМ) тогда равен Mst = –MΣpm.
Если условиться, что ТСМ будет реализован двумя дополнительными стабилизирующими трастерами, установленными на расстоянии Lst друг от друга (один на передке, другой на корме корпуса – см. рис. 1), то требуемая тяга каждого из них определится уравнением:
2.3. Мощности и энергозатраты в МПДК
Мощность реализации горизонтальных сил воздействия среды движения (СВСД), в соответствии с (3):
Напомним важное из работы : Vq – являясь скоростью горизонтального перемещения экипажа, одновременно характеризует скорость передачи энергии от мобильного объекта в среду движения.
Подъемные силы ТПС и АПС различаются по физической сути их формирования (и сопутствующих преобразовательных процессов): ТПС – феномен прямого контактного воздействия вертикальной компоненты траста КД на корпус ТС в точке приложения (либо возникновения) траста (ТПТ), а АПС – результат опосредованного (через форм-фактор корпуса ТС) вертикального воздействия воздушной среды на ТС, сфокусированного в его ЦД (в комбинации Fwz c Fwx ). Если ТПС зависит только от произвола управляющего сигнала и напрямую не зависит ни от профиля квантомобиля, ни от его скоростного и нагрузочного режимов, то АПС напротив – является функцией аэродинамического качества экипажа (Kаэр = cl/cd) и скоростного режима ТС.
Исходя из этого, мощность процесса реализации ТПС будет определяться посредством предопределенного («паспортного») ЭЦВТ КД, т.е. NFTz = FTz·KNFtz (где KNFtz = const не зависит от скорости ТС и верно даже для неподвижно висящего ТС).
Вид же мощности реализации АПС качественно иной: из равенства Fwz = Fwx·(cl/cd) (в обусловленном для модели диапазоне скоростей) следует
Можно даже записать:
В итоге мощность реализации СПС:
Поддержка ТСМ требует энергозатрат. Мгновенная мощность, реализуемая системой из двух трастеров, (несмотря на разнонаправленность их тяги), равна: NFst = 2·|Fst|·KNFst , где KNFst – ЭЦВТ стабилизирующего трастера ([Вт/Н]).
Компонентные энергозатраты определяются интегралами мощностей реализации рассмотренных сил по времени рассмотрения процессов. Общие энергозатраты определяются скалярной суммой компонентных энергозатрат.
2.4. Программное обеспечение МПДК
Структура имитационной системы представлена в . Она состоит из пяти подсистем: Vectored_Thrust – для выработки сценариев реализации во времени задающего вектора FT(t) и угла β(t); Longitudinal Dynamics – расчета показателей динамики продольного движения экипажа (см. , ); Reactions&Moments – расчета силовых моментов в плоскости тангажа (см. ); Vertical Dynamics – динамики вертикального движения экипажа (см. ); Energetics – расчета показателей энергетики движения (продвинута относительно ).
Отметим наличие множества дисплеев и осциллографов (в терминологии Simulink-Matlab) в подсистеме Energetics (рис. 2) – для детального анализа и вывода результатов расчетов.
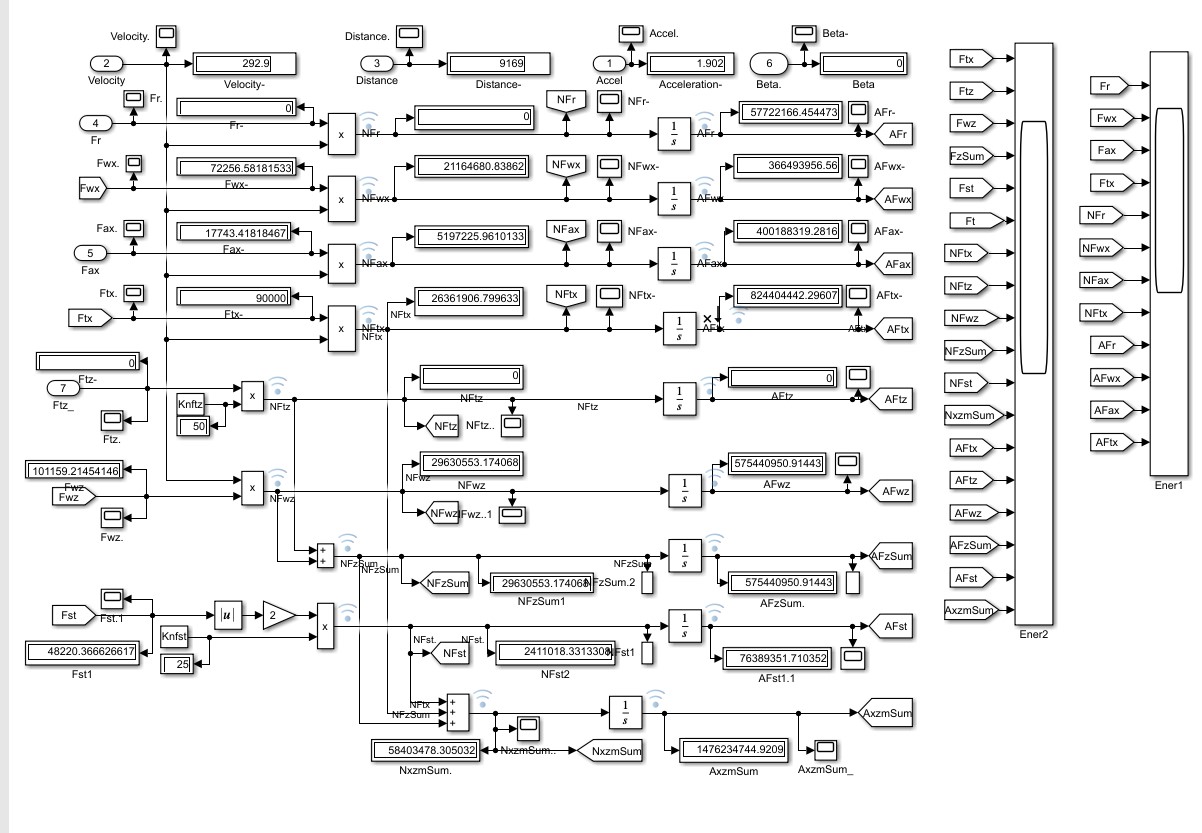
Рисунок 2 - Модуль ПРЭ Energetics
3. Результаты расчета показателей движения квантомобиля
3.1. Настройка моделей квантомобилей
Для отработки ПРЭ, а затем проведения ПИМ взлета квантомобиля привлекли две крайних макромодели из ряда «плохообтекаемых тел» (ПОТ) (bluff bodies) : 1-Box и Davis (ранее использованных автором в исследовании ). ПОТ 1-Box (с габаритами грузовика КамАЗ-4326), с низкими аэродинамическими свойствами (cd = 0,5; cl = 0; Каэр = cl/cd = 0 – т.е. с отсутствием АПС), в крайне тяжелых дорожных условиях (fk0 = 0,3). ПОТ Davis с превосходной аэродинамикой (cd = 0,263; cl = 0,42; Каэр = cl/cd = 1,6 – т.е. со значительной АПС) в крайне легких условиях горизонтальной ОП (fk0 = 0,02). Профили этих ПОТ представлены в .
В табл. 1 помещены основные параметры моделей. В ней L, W и H – габаритные длина, ширина и высота моделей, соответственно; Hg и Hw – высоты центра тяжести (ЦТ) и центра аэродинамического давления; rd – радиус колес. Sfr1 и Sfr2 – фронтальная (лобовая) площадь экипажа в наземном и в летном вариантах, м2; Spl1 и Spl2 – площадь в плане экипажа в наземном и в летном вариантах, м2.
Для обоих вариантов ПОТ приведенные параметры подвески: cup = 600000 Н/м, kam = 32000 Нс/м .
Таблица 1 - Основные данные по моделям 1-Box и Davis
Параметр | 1 | 2 |
1-Box | Davis | |
L, м | 7,3 | 7,3 |
W, м | 2,55 | 2,55 |
H, м | 3,3 | 1,87 |
Sfr1, м2 | 8,5 | 4,76 |
Sfr2, м2 | 8,5 | 5,5 |
Lwb, м | 4,25 | 4,87 |
L2, м | 2,125 | 2,435 |
Hg, м | 1,3 | 0,9 |
Hw, м | 1,46 | 1,0 |
rd, м | 0,5 | 0,5 |
m, кг | 8970 | 8970 |
Gq, Н | 87995,7 | 87995,7 |
FT, Н | 90000 | 90000 |
cd1 | 0,5 | 0,263 |
cd2 | 0,4 | 0,25 |
cl1 | 0 | 0,42 |
cl2 | 0,05 | 0,35 |
cm1 | 0 | –0,35 |
cm2 | –0,05 | –0,2 |
cdv1 | 0,8 | 0,6 |
cdv2 | 0,7 | 0,5 |
Spl1, м2 | 18 | 15 |
Spl2, м2 | 24 | 22 |
fk0 | 0,3 | 0,02 |
fkv, с2/м2 | 0,00037 | 0,00037 |
Lst, м | 7 | 7 |
KNFtz, Bт/Н | 50 | 50 |
KNFst, Bт/Н | 25 | 25 |
ЦТ обеих моделей расположили в их срединных плоскостях колесной базы (L2=Lwb/2, где Lwb – колесная база, а L2 – расстояние от ЦТ до вертикальной плоскости задней оси). Точку приложения траста расположили в ЦТ.
Значения ЭЦВТ установили на основе обработки данных исследований , , , и др., обобщенных автором в работе : для тягового трастера КД KNFtz = 50 Bт/Н; для стабилизирующего трастера – KNFst = 25 Bт/Н.
В целях обеспечения возможности продольного движения экипажа весом 88 кН при его полном вывешивании выбрали траст FT = 90 кН (обосновано в , ). Во всех расчетных реализациях взлета рост траста с нуля до 90 кН происходит за 5 секунд.
3.2. Расчетные действия
Для мелких серийных графиков с отсутствующими размерностями по осям (на рис. 4 ÷ 8) установили следующие размерности величин: для сил Fr, Fwx, Fax, FTx, FTz, Fwz, FzSum, Fst, FT – Н; для мощностей NFr, NFwx, NFax, NFTx, NFTz, NFwz, NFzSum, NFst, NxzmSum – Вт; для энергозатрат AFr, AFwx, AFax, AFTx, AFTz, AFwz, AFzSum, AFst, AxzmSum – Дж. Ось времени – в с. При обсуждении результатов расчетов конкретика размерностей может меняться. NxzmSum и AxzmSum – суммарные мощность и энергозатраты (скалярные суммы компонентных показателей).
Расчетные действия начали с построения графиков изменения вертикальной координаты pz взлета ПОТ 1-Box и Davis при FT = 90 кН и различных углах наклона вектора траста β – рис. 3. На этом рисунке для угла β = 77,9° показаны значения времени подъема экипажей t10м и t25м на высоты Hlf2 = 10 м и Hlf3 = 25 м, соответственно.
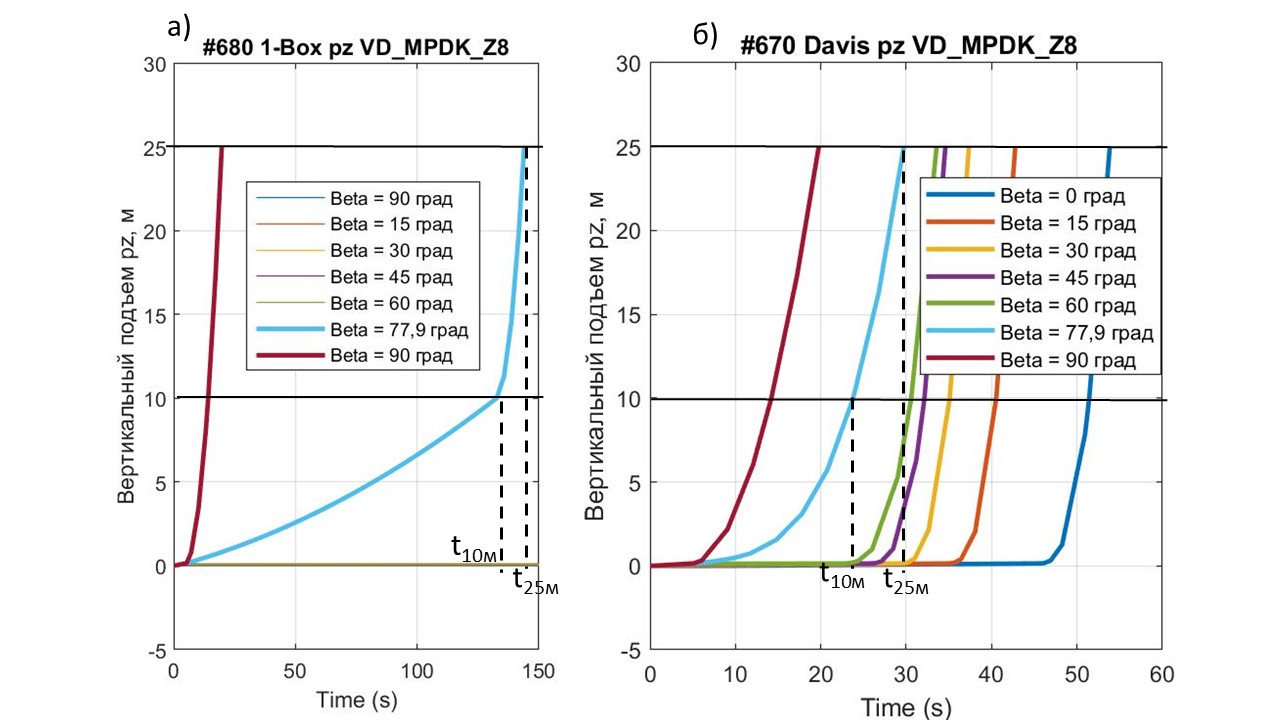
Рисунок 3 - Графики изменения координаты pz взлета ПОТ при FT = 90 кН и различных углах наклона вектора траста β:
а - 1-Box; б - Davis
Затем рассмотрели в деталях (реализация сил, мощностей и энергозатрат) лифт до высоты Hlf3 = 25 м с приложением к ПОТ вертикально направленного траста, без горизонтального движения экипажа (FT = 90 кН, β = 90°) – рис. 4.
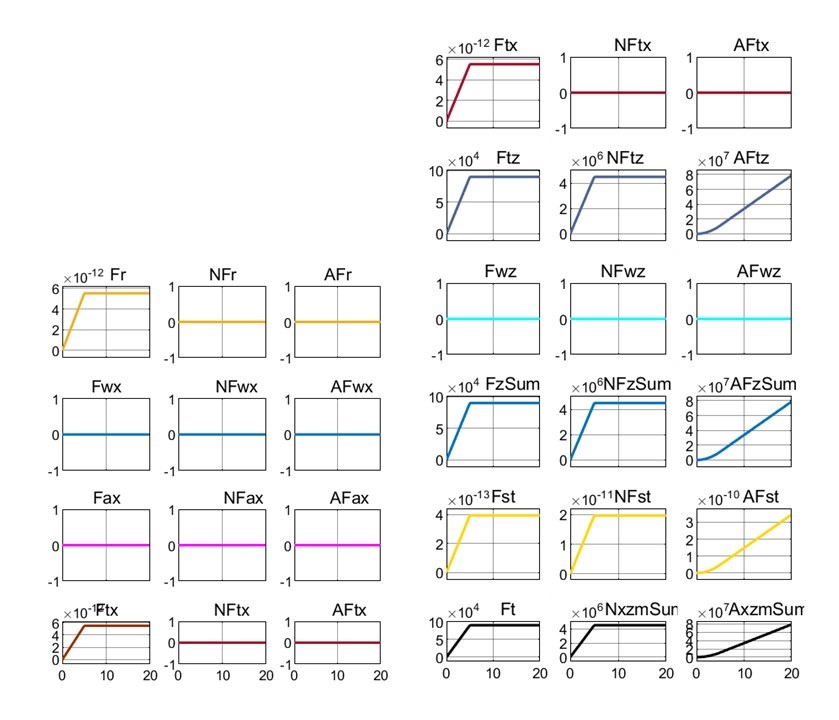
Рисунок 4 - Реализация сил, мощностей и энергозатрат при взлете модели 1-Box под воздействием траста FT = 90 кН и β = 90° до высоты Hlf3 = 25 м
На рис. 5 отображена реализация сил, мощностей и энергозатрат при взлете модели 1-Box под воздействием траста FT = 90 кН и β = 77,9° до высоты Hlf3 = 25 м.
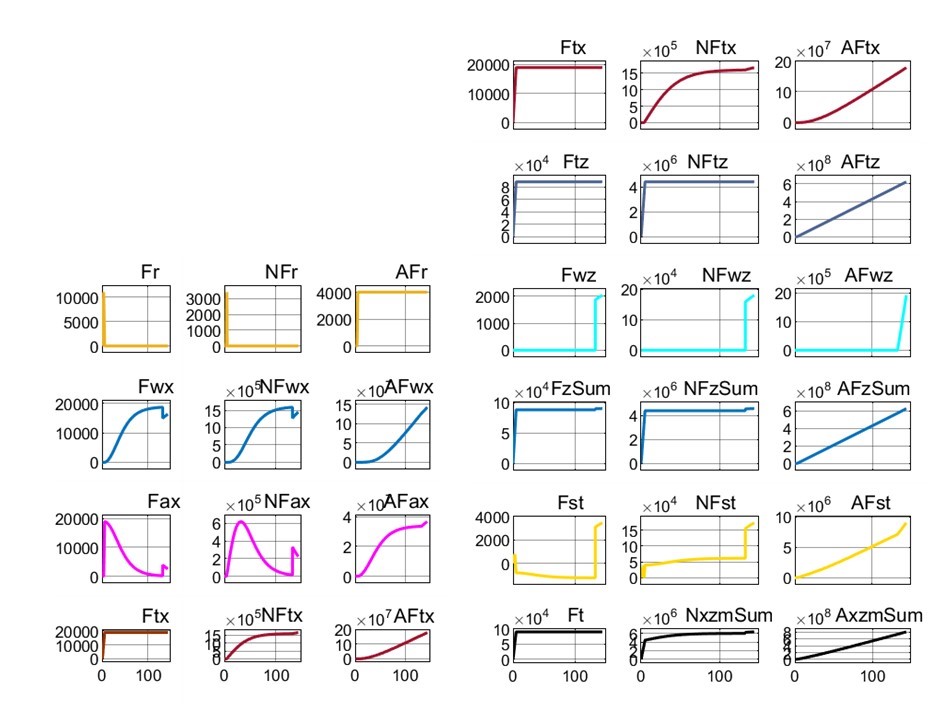
Рисунок 5 - Реализация сил, мощностей и энергозатрат при взлете модели 1-Box под воздействием траста FT = 90 кН и β = 77,9° до высоты Hlf3 = 25 м
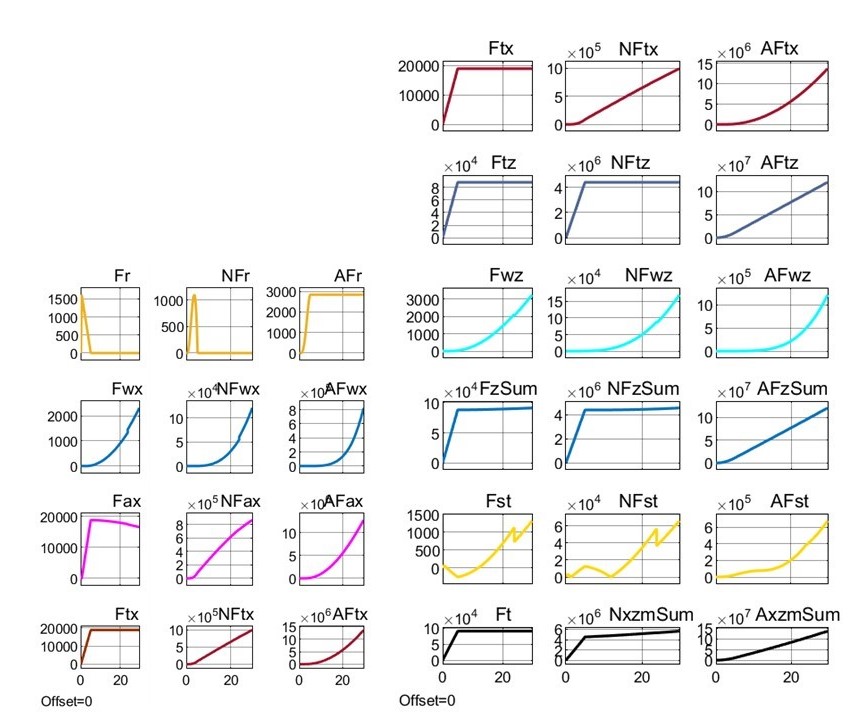
Рисунок 6 - Реализация сил, мощностей и энергозатрат при взлете модели Davis под воздействием траста FT = 90 кН и β = 77,9° до высоты Hlf3 = 25 м
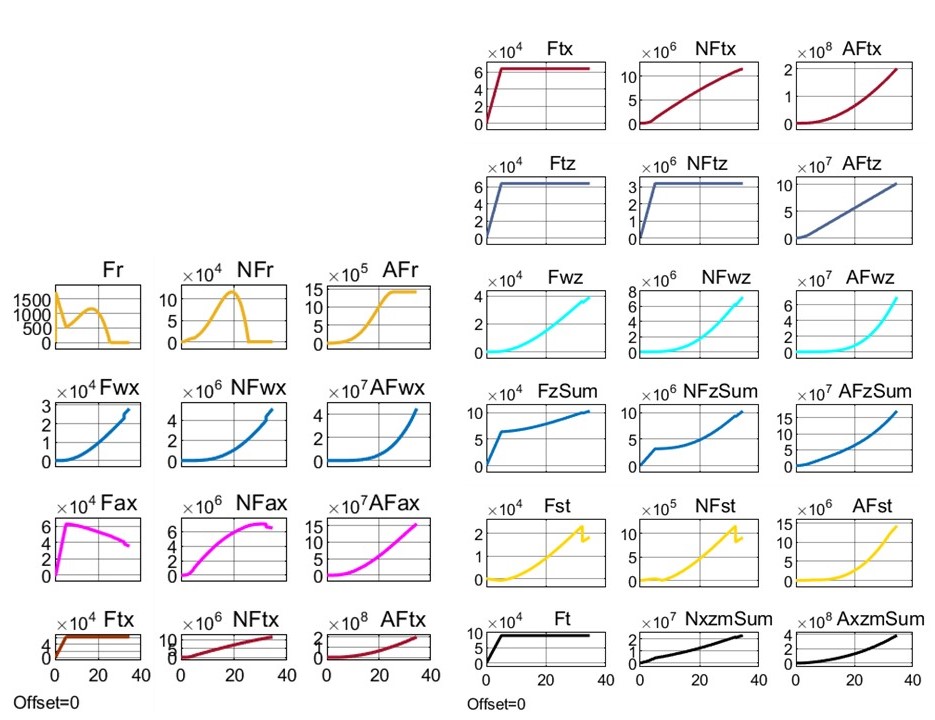
Рисунок 7 - Реализация сил, мощностей и энергозатрат при взлете модели Davis под воздействием траста FT = 90 кН и β = 45° до высоты Hlf3 = 25 м
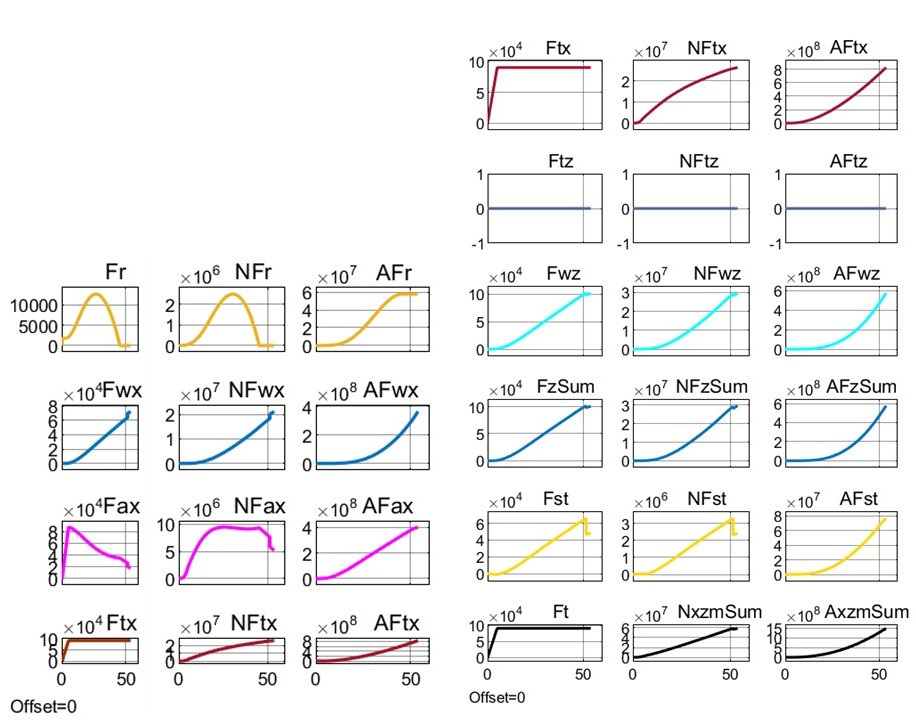
Рисунок 8 - Реализация сил, мощностей и энергозатрат при взлете модели Davis под воздействием траста FT = 90 кН и β = 0° до высоты Hlf3 = 25 м
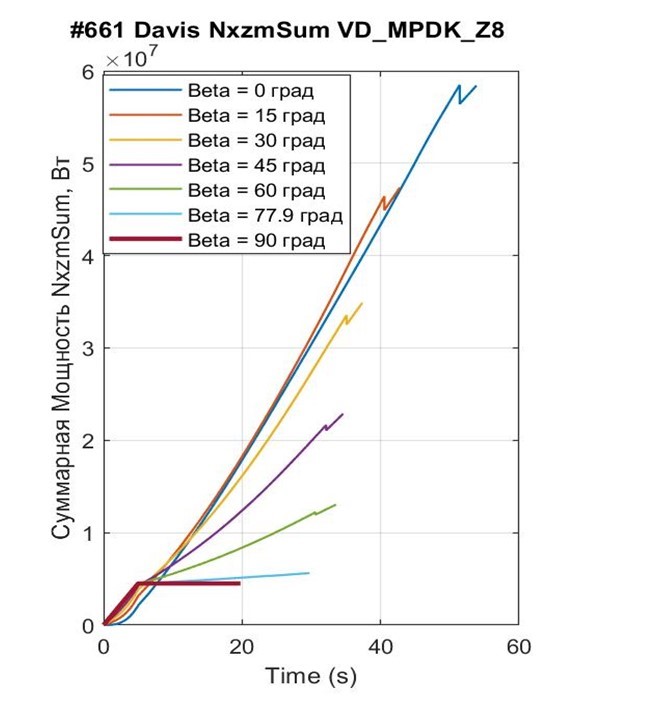
Рисунок 9 - Реализация суммарной мощности NxzmSum при взлете модели Davis под воздействием траста FT = 90 кН и β = 0° ÷ 90° до высоты Hlf3 = 25 м
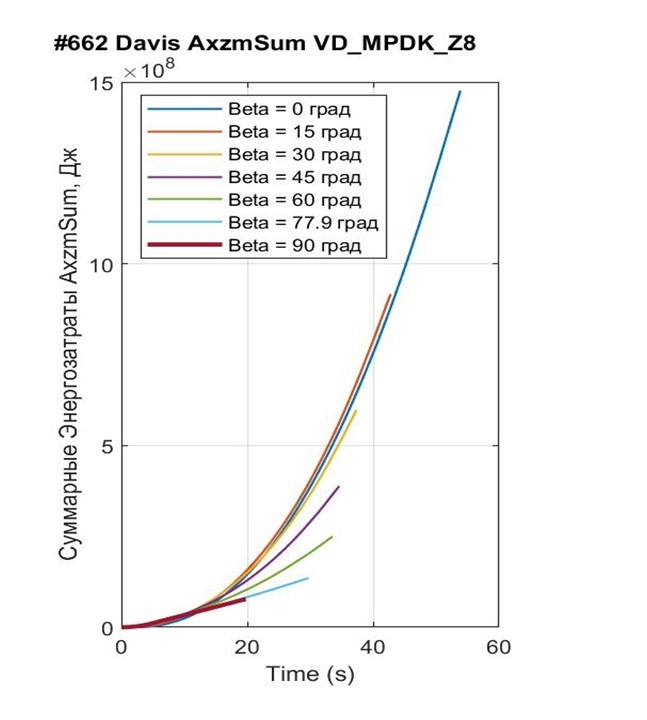
Рисунок 10 - Реализация суммарных энергозатрат AxzmSum при взлете модели Davis под воздействием траста FT = 90 кН и β = 0° ÷ 90° до высоты Hlf3 = 25 м
4. Обсуждение результатов расчетов
4.1. Сравнение энергозатрат 1-Box и Davis
Анализ графиков изменения координаты pz взлета ПОТ 1-Box и Davis на рис. 3 показал существенную разницу между этими крайними по профилю и нагруженности вариантами ПОТ. Отсутствие АПС Fwz у ПОТ 1-Box (при cl = 0) и всего лишь двухпроцентный запас тяги траста FT над весом экипажа Gq (90 кН против 88 кН) обусловили возможность отрыва колес этого экипажа от ОП лишь при углах β = 77,9° ÷90° (см. рис. 3.а). Более эффективные подъемы с расширением диапазона значений угла β, естественно, будут происходить при тяге траста FT > 90 кН. Однако ограничились в данном исследовании FT = 90 кН – достаточной величиной траста для выявления отличий энергозатрат сравниваемых вариантов движения частично вывешенного квантомобиля.
Как отмечалось, при β = 90° темп подъема сравниваемых ПОТ мало чем отличается (t25 = 19,94 для 1-Box и t25 = 19,90 для Davis) – это объясняется отсутствием АПС при vx ≈ 0 также и у Davis; и весьма малым влиянием разницы конфигураций экипажей в плане (Spl и cdv) при малых вертикальных скоростях vz. При вертикальном взлете, естественно, NFTx= 0, AFtx= 0 (см. рис 4); NFst = 0, AFst = 0 (поскольку силы Gq, FTz приложены в ЦТ, а FTx = 0). Реализуемая суммарная мощность NxzmSum = NFzSum = 4500 кВт, а энергозатраты на подъем до высоты 25 м (зависящие в данном случае только от ЭЦВТ) AxzmSum = AFzSum = 78 588 кДж (у 1-Box), 78 482 кДж – у Davis.
Таблица 2 - Показатели сил, мощности и энергозатрат ПОТ 1-Box и Davis на финишный момент взлета t25 на высоту 25 м под воздействием траста Ft = 90 кН при различных углах его наклона β
Динамика и энергетика взлета при β = 77,9° для сравниваемых ПОТ уже значительно отличается – см. рис. 3; варианты 2 и 4 в табл. 2; сравни также рис. 5 и 6. Время взлета для 1-Box t25 = 144 c, а для Davis t25=29,7 с.
Сравнивая, например, для β = 77,9° рис. 5 (1-Box) и рис.6 (Davis), можно отметить следующее:
1) при одинаковой и постоянной горизонтальной силе тяги FTx=18,86 кН характер изменения мгновенной мощности NFTx и реализуемые её значения существенно отличаются;
2) значения совершенной этой силой работы AFTx до выхода на высоту 25 м отличаются на порядок: 178 450 кДж у 1-Box и 13 647 кДж у Davis.
Проведем анализ отличий компонентных сил, мощностей и энергозатрат ПОТ 1-Box и Davis при взлете на высоту 25 м под воздействием траста Ft = 90 кН при угле его наклона β = 77,9° (см. рис. 5 и 6, также варианты 2 и 4 в табл. 2).
Сила сопротивления качению колес Fr = 0 почти на всей дистанции разгона для обоих ПОТ (экипаж вывешен вместе с колесами), за исключением силового пика и энергозатрат на реализацию силы страгивания экипажа с места (см. AFr = 4 кДж и AFr = 2,8 кДж в табл. 2).
Характер изменения сил фронтального сопротивления воздуха Fwx существенно отличается (см. рис. 5 и 6) и к тому же на разных дистанциях разгона для ПОТ приводят к значительной разнице энергозатрат (AFwx = 141 838 кДж и AFwx = 836,2 кДж в табл. 2).
Энергозатраты на преодоление сил инерции прямо связаны с конечной скоростью ускоренного разбега (см. vx= 88,6 и 52,4 м/с в табл. 2), и зафиксированы на уровне AFax = 36 608 кДж и AFax = 12 818 кДж.
В результате при FTx = Fr + Fwx + Fax = 18.86 кН для обоих ПОТ, энергозатраты AFtx на горизонтальное перемещение при взлете до 25 м: для 1-Box 178 450 кДж, для Davis 13 647 кДж.
Энергозатраты на висение экипажа при силе вывешивания экипажа (ТПС) FTz =
88кН и обеспечивающей её мощности NFTz = 4 400 кВт (при KNFtz = 50 Вт/Н) напрямую зависят от времени висения (t25 за минусом времени от начала разбега до отрыва колес). Эти затраты равны 632 342 кДж и 119 815 кДж.
Энергозатраты на обеспечение АПС Fwz равны 1 927 кДж и 1 215 кДж, причем для 1-Box эти затраты связаны только со вторым («лётным») профилем (на высотах от 10 до 25 м).
В величине FzSum = FTz + Fwz в данных примерах (при Gq = 88 кН и Ft=90 кН) составляющая FTz определяет в основном динамику вывешивания экипажа до отрыва колес от ОП, а Fwz – динамику дальнейшего взлета (см. ). Энергозатраты зависят от времени висения t25.
Противоположно направленные силы Fst (см. рис. 1), непрерывно меняющие свою величину (компенсируя динамический питч-момент) и этим обеспечивающие постоянную стабилизацию экипажа в процессе взлета (см. рис. 5 и 6), требуют энергозатрат на динамическую реализацию этой пары сил (при KNFst = 25 Вт/Н) 8 993 кДж и 677 кДж (см. табл. 2).
В итоге суммарные энергозатраты на взлет (AFxzmSum = AFTx + AFzSum + AFst) при β = 77,9 ° до 25 м ПОТ 1-Box составили 811 712 кДж, а на взлет Davis – 135 354 кДж, т.е. с шестикратной разницей
4.2. Оценка энергозатрат Davis для различных стратегий взлета
Оценим энергозатраты взлета ПОТ Davis на высоту 25 м под воздействием траста FT = 90 кН при нескольких постоянных углах его наклона β – привлекаем данные табл. 2, варианты 3 ÷ 6.
Видим, что с уменьшением угла наклона β (90° – 77, 9° – 45° – 0°) время взлета t25 увеличивается (19,9 – 29,7 – 34,6 – 53,8), финишная продольная скорость vx увеличивается (0 – 52,4 – 182 – 293), горизонтальный путь sx увеличивается (0 – 725 – 3178 – 9169), что естественно. Как следствие, энергозатраты на преодоление горизонтальных сил сопротивления FTx увеличиваются (0 – 13647 – 201831 – 824404 кДж), функция энергозатрат на вывешивание и поддержку висения ТПС FTz имеет выпуклый характер (78482 – 119815 – 102098 – 0 кДж), энергозатраты на АПС Fwz увеличиваются (0 – 1215 – 69715 – 575441 кДж), энергозатраты на стабилизацию экипажа Fst увеличиваются (0 – 677 – 14370 – 76389 кДж), суммарные энергозатраты на взлет FxzmSum увеличиваются (78 482 – 135 534 – 388 014 – 1 476 235 кДж).
Факт того, что сценарии управления вектором траста FT с более пологим углом наклона β приводят к более длительному времени взлета t25, но при этом, однако, одновременно обеспечивают более продвинутое курсовое перемещение экипажа sx, приводит к постановке простейшей оптимизационной задачи: рассмотреть варианты достижения определенной точки траектории движения экипажа (pz, sx) с привлечением в качестве критерия эффективности t25 , либо vx, либо суммарные энергозатраты FxzmSum.
В качестве примера, рассмотрим движение к опорной точке (pz, sx) = (25 м, 725 м) (см. вариант 4, β = 77,9° в табл. 2) под действием того же траста FT = 90 кН, но, однако, с реализацией комбинированного временнóго сценария изменения угла β: {t = 0, 5, 19, 20, 21, 40; β = 90, 90, 76, 73, 70.15, 70.15}. Несмотря на кусочно-линейный характер изменения этого задающего вектора управления FT, траектория движения экипажа – довольно гладкая (см. рис. 11).
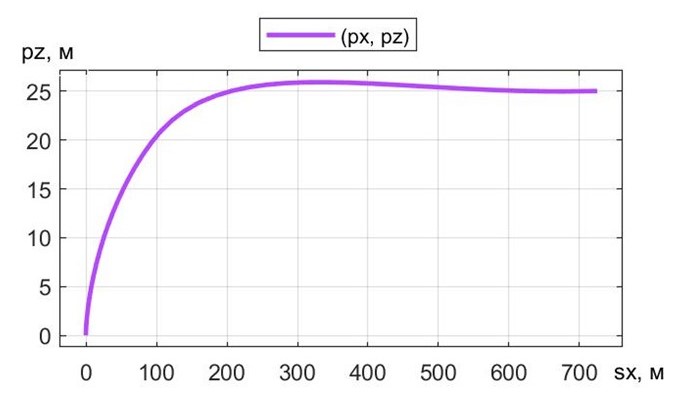
Рисунок 11 - Траектория движения ПОТ Davis к точке pz = 25 м, sx = 725 м с реализацией комбинированного сценария изменения угла β
5. Заключение
Разработанная в среде авторской Simulink-модели приземного движения квантомобиля (МПДК) Подсистема расчета энергозатрат (ПРЭ) Energetics позволяет проводить расчетное исследование энергозатрат: как на преодоление продольных сил сопротивления движению, так и на вертикальное вывешивание экипажа с обеспечением его устойчивости в плоскости тангажа.
Эта модель, по мнению автора, должна стать, во-первых, базой для оптимизационных расчетов взлета квантомобиля во многообразии его конфигураций и условий движения по ОП и рельефу местности, а во-вторых, – составной частью алгоритмов расчета динамических и траекторных показателей произвольного движения квантомобиля.
На базе проведенных посредством МПДК с ПРЭ расчетов и их анализа преодолена познавательная сложность компонентного представления энергозатрат при взлете квантомобиля в плоскости тангажа.
Проведенное исследование позволило утвердиться в гипотезе: при исследовании энергозатрат на взлет квантомобиля возможно расщепленное представление этих затрат по видам продольных и вертикальных составляющих траста и сил воздействия среды движения на экипаж – со сведением компонентных энергозатрат в их скалярную сумму.
Дальнейшие исследования должны быть направлены на рассмотрение возможности применения развиваемого подхода к оптимизации траекторий движения квантомобилей, возможно, главным образом, беспилотных. Для этого понадобится, в первую очередь, привлечение комбинирования величинами и углами траста c использованием оптимизационных методов.
