Моделирование системы ориентации и стабилизации малого космического аппарата

Система управления ориентацией и стабилизации (СУОС) играет важную роль в процессе функционирования современных космических аппаратов (КА), так как от ее характеристик во многом зависит возможность выполнения целевых задач, возложенных на КА. Поиск эффективных средств управления ориентацией и стабилизацией КА является одной из главных задач исследований в области ракетно-космической техники. Критерии эффективности системы управления выбираются в соответствии с задачами космических миссий, которые должны быть решены определенным КА

Выбор СУОС выполняется на основе имеющейся информации об исполнительных элементах, эффективности, надежности, массе, стоимости, энергопотреблении и алгоритме управления КА. Кроме того, следует отметить, что при разработке систем управления необходимо удовлетворить целому ряду требований. Не перечисляя всех из них, отметим, что определяющим и наиболее сложным является требование удовлетворения проектируемой системой необходимых характеристик по точности. Сложность создания системы, которая будет обеспечивать заданную точность заключается в том, что на этапе технической реализации синтезированного алгоритма управления и при дальнейшей эксплуатации системы в целом неизбежно проявятся сделанные на этапе разработки упрощения и идеализации реального объекта и условий его функционирования. При создании СУОС широко используются методы классической теории управления и оптимального управления, предполагающие наличие точной математической модели объекта управления

Таким образом, неточность и неполнота сведений о реальном объекте управления и возможных возмущениях, которые будут действовать на него, могут привести к ситуации, когда оптимально рассчитанная система при одних параметрах может потерять свои свойства оптимальности или вообще оказаться непригодной для эксплуатации при других. Указанные обстоятельства предопределяют необходимость применять такие методы синтеза алгоритмов управления, которые позволили бы получать гарантированную точность управления в условиях неопределенности в описании динамического объекта.

Принимая во внимание вышеизложенное, разработка эффективного алгоритма и изучение основных принципов функционального исполнения систем ориентации и стабилизации КА представляет собой на сегодняшний день важную научно-практическую задачу, необходимость решения которой и предопределила выбор темы данной статьи.

Вопросы синтеза адаптивной системы стабилизации КА в орбитальной системе координат прорабатываются такими авторами как: Садуахас А.К., Калманова Д.М., Хамитова Д.Р., Султанова С.С., Керимбай Н.Н., Ергалиев Д.С., Brewer, John Matthew; Tsiotras, Panagiotis; Mirshams, M.; Khosrojerdi, M.

Алгоритмы управления точной стабилизацией, ориентацией и маневрами космических аппаратов нашли свое отражение в работах Горелко М.Г., Мурыгина А.В., Богатыревой С.М., Илюхина С.Н., Топоркова А.Г., Kosari, A.; Jahanshahi, H.; Razavi, S.A.; Gui, H.; Jin, L.; Xu, S.

Особенности реализации отказоустойчивого управления реактивным колесом для стабилизации ориентации космического аппарата со сходимостью по конечному времени изучаются Бирюковой М.В., Туфаном А., Ермаковым В.Ю., Аппазовой Ш., Ергалиевым Д.С., Мукановой К., Советкажиевым А., Ракишев Ж.Б., Nabi, M.; Al-Saggaf, Ubaid M.; Bettayeb, Maamar.

Однако, несмотря на имеющиеся труды и наработки, ряд проблемных вопросов в данной предметной плоскости остаются открытыми. В частности, отдельного внимания заслуживают перспективы использования методов машинного обучения и компьютерного моделирования для повышения эффективности интеллектуального управления ориентацией космических аппаратов. В дальнейшем развитии и усовершенствовании нуждается математическая модель управляемого движения материальной точки в центральном гравитационном поле.

Итак, цель статьи заключается в рассмотрении особенностей моделирования системы ориентации и стабилизации космического корабля на примере малого космического аппарата.

2.1. Составляющие системы угловой ориентации и стабилизации МКА

Ключевым элементом любой системы ориентации и стабилизации является объект управления и регулятор. Объектом управления в рамках проводимого исследования будет выступать малый космический аппарат (МКА). Система стабилизации поддерживает постоянными или изменяет по определенному закону угловое положение МКА. Регулятор – это комплекс автоматически действующих устройств и механизмов, который осуществляет управление объектом управления. Стабилизация и ориентация МКА призваны обеспечивать точное наведение его антенны высокого усиления на Землю для связи, выбор правильных координат бортовых приборов для сбора и последующей интерпретации данных, разумное использование нагревающих и охлаждающих эффектов солнечного света и тени для терморегулирования

Как показывает анализ литературных источников несмотря на то, что системы ориентации и стабилизации значительно отличаются между собой по конструкции, выполняются они по типовым функциональным схемам. При этом в большинстве современных систем управление осуществляется по отклонению управляемой величины от заданного настройкой ее значения или от заданного закона ее изменения.

В свою очередь на практике используются следующие системы ориентации МКА:

1.     Активная магнитная ориентация.

2.     Реактивные системы ориентации.

3.     Маховиковые системы ориентации.

4.     Гиросиловые системы ориентации.

5.     Робастные системы ориентации.

На рис. 1 приведен пример функциональной схемы трех плоскостной системы ориентации и стабилизации.

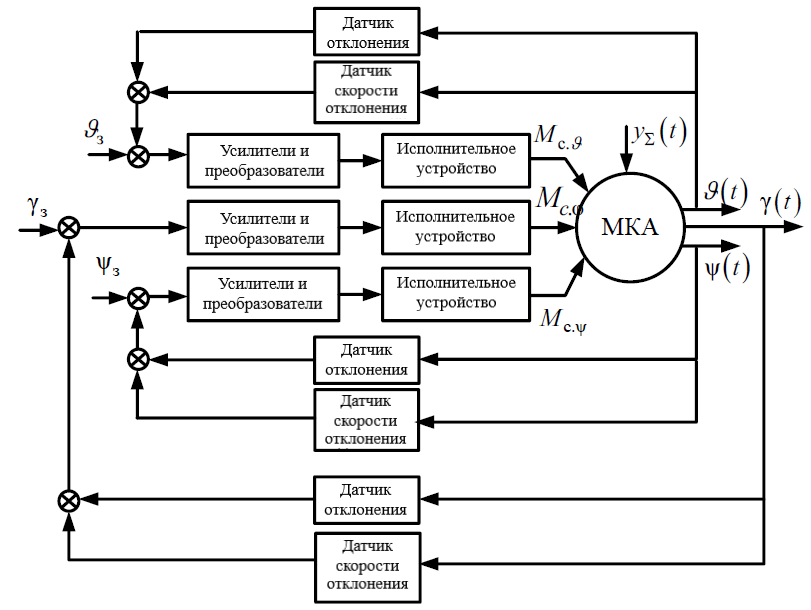
Рисунок 1 - Функциональная схема системы ориентации и стабилизации

DOI:10.23670/IRJ.2024.141.65.1

На рисунке 1 используются следующие условные обозначения:  – угол тангажа;  – угол крена;  – угол рыскания;  – моменты возмущения;  – момент стабилизации.

Для описания углового движения МКА используем инерциальную систему координат (ИСК) OI xI yI zI с началом в центре масс Земли OI. Ось OI yI ИСК направлена по оси вращения Земли, а ось OI zI - в точку весеннего равноденствия в заданную эпоху. Используем также связанную с МКА систему координат (CСК) Og xg yg zg с началом в центре масс и осями, которые совпадают с главными центральными осями инерции МКА.

Уравнение вращательного движения абсолютно жесткого МКА может быть представлено следующим образом:

(1)

где J – тензор инерции МКА;  – вектор абсолютной угловой скорости МКА, заданный проекциями на оси ССК; Md, Mc – векторы суммарного возмущающего и управляющего моментов.

Переход от ИСК к ССК можно определить последовательностью поворотов  на углы. В этом случае кинематические уравнения, связывающие вектор абсолютной угловой скорости МКА и производные углов ориентации, могут быть представлены в таком виде

(2)

Таким образом, все отклонения МКА от начального положения определяются отклонениями триэдра, который жестко связан с аппаратом, от триэдра инерциальной системы координат. Положение связанных осей Og xg yg zg относительно OI xI yI zI целиком определяется тремя независимыми углами (рис. 2):   –угол тангажа;  – угол крена;  – угол рыскания. Следовательно, движение МКА будет определено, когда будет известно изменение трех углов во времени .

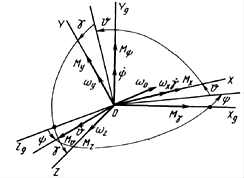
Рисунок 2 - Переход от инерциальной к связанной системе координат

DOI:10.23670/IRJ.2024.141.65.2

Далее, при проведении численных экспериментов, будем считать, что уравнения (1), (2) точно описывают динамику МКА. Уравнения (1), (2) существенно нелинейны, но для малых угловых отклонений МКА значения производных углов ориентации примерно равны , значит уравнения (1), (2) могут быть представлены в линейной форме в виде трех независимых дифференциальных уравнений:

(3)

где Jx, Jy, Jz  – центральные моменты инерции МКА относительно соответствующих осей ССК;  –проекции векторов суммарного возмущающего и управляющего моментов на соответствующие оси ССК. Будем считать, что именно модель (3) известна до вывода МКА на орбиту.

2.2. Оптимальное управление

Для синтеза регулятора уравнение (3) можно представить в форме пространства состояний в таком дискретном виде:

(4)

где  –векторы состояния и управления на k-м такте управления, соответственно.

Матрицы состояния и управления, которые входят в представление (4), имеют вид:

Для оценки качества управления используем такой квадратичный критерий, который учитывает точность управления и затраты на управление:

(5)

где Q и F – весовые матрицы. 

Для такого критерия, управление может быть найдено в форме линейно-квадратичного регулятора:

(6)

Матрица коэффициентов усиления регулятора K находится путем решения алгебраического уравнения Риккати

(7)

в таком виде:

где P – решение уравнения (7).

2.3. Синтез алгоритмов стабилизации МКА. Метод декомпозиции

Для решения задачи синтеза синтез алгоритмов стабилизации МКА воспользуемся аналогом метода синтеза управления движением КА относительно центра масс. Представим систему линейного приближения уравнений движения материальной точки в отклонениях от координат, записанных в форме Коши:

(8)

в виде подсистем кинематических и динамических уравнений, введя обозначения:

 Тогда систему уравнений (8) запишем в виде: 

(9)

Далее используем «кинематическую» функцию Ляпунова (ФЛ)

(10)

В соответствии с уравнениями (9) производная ФЛ (10) имеет вид:

(11)

Считая в (11) скорость V управлением, выберем «управление»:

(12)

где матрица , например . При этом производная  и поэтому норма вектора отклонения от заданной точки будет монотонно уменьшаться 

Далее для завершения решения задачи синтеза стабилизирующего управления выберем «динамическую» ФЛ в виде:

(13)

Производная ФЛ (13), учитывая второе уравнение из системы (9), имеет вид: 

Предполагая:

(14)

получаем: 

(15)

Из соотношения (15) следует, что ФЛ wd является экспоненциально убывающей функцией и в результате отклонение МКА от заданной точки будет убывать: . Из уравнения (12) с учетом (9) следует:

(16)

Подставив в (14) значения  и  из (12), (16), последовательно получаем:

Таким образом, подводя итоги проведенного исследования, можно сделать следующие выводы. Проблема обеспечения требуемого качества управления МКА в условиях неполной априорной информации о внешних воздействиях и параметрах объекта управления может быть решена путем применения адаптивных систем управления с наблюдателем состояния. Для повышения эффективности управления системой ориентации и стабилизации МКА целесообразно применять методы, которые основаны на использовании развитого формализма построения внешних эллипсоидальных оценок множеств досягаемости и предельных множеств линейных динамических систем, структурно возмущенных действием немоделированных ограниченных воздействий окружающей среды.