Метод анализа временных рядов и его математическая модель в программном обеспечении
Метод анализа временных рядов и его математическая модель в программном обеспечении
Аннотация
В данной статье представлен обзор методов анализа временных рядов и их математических моделей, а также их реализация в программном обеспечении. Основное внимание уделяется основным подходам к моделированию и прогнозированию технического состояния изделия авиационной техники временными рядами, а также их применению на практике. Также в статье рассмотрены вопросы эффективности и точности прогнозов, получаемых с использованием данных методов. В данной статье рассмотрены методы анализа временных рядов, включая модели авторегрессии и скользящего среднего (ARIMA), и их применение для прогнозирования количества отказов бортового оборудования на самолете А320. Рассмотрены основные шаги, необходимые для построения модели ARIMA, включая подбор параметров, оценку модели и генерацию прогнозов. Результаты показывают, что модель ARIMA может быть эффективным инструментом для прогнозирования количества отказов бортового оборудования на самолете, что может помочь в оптимизации процессов обслуживания и ремонта. Модель ARIMA (2.1.1) показала сравнительно высокие значения погрешностей (MAE и RMSE) и низкий коэффициент детерминации (R^2). Это указывает на то, что модель может быть недостаточно точной для предсказания количества отказов оборудования на основе доступных данных. Следовательно, необходимо усовершенствовать методику сбора и обработки данных используемых для прогнозирования, что в свою очередь повысить качество и точность модели ARIMA.
1. Введение
В данной статье рассматриваются методы анализа временных рядов и их применение для прогнозирования количества отказов бортового оборудования на самолете А320. Несмотря на то, что моделирование временных рядов является сложной задачей, современные методы и технологии делают эту задачу более доступной для исследователей и практиков. Анализ временных рядов является важным инструментом в области прогнозирования и анализа данных, который находит применение в различных сферах, включая авиацию и оборудование. Другие применения анализа временных рядов включают прогнозирование спроса на товары и услуги, анализ финансовых рынков, прогнозирование погоды и многое другое. Однако, необходимо отметить, что моделирование временных рядов является сложной задачей, требующей глубоких знаний в области математической статистики и программирования. Тем не менее, благодаря развитию современных методов и технологий, а также наличию доступных программных средств, применение моделей временных рядов становится все более распространенным. Прогнозирование с использованием этих моделей может помочь в принятии важных бизнес-решений и оптимизации процессов, что в конечном итоге может привести к существенному увеличению эффективности и производительности в различных отраслях. Ключевыми преимуществами моделей временных рядов являются их способность обнаруживать скрытые закономерности в данных, а также возможность учесть влияние факторов, изменяющихся во времени. Таким образом, анализ временных рядов остается важным инструментом в современном мире и может привести к значительным улучшениям в различных областях деятельности.
1.1. Литературный обзор и обоснование актуальности проблемы
В последние годы анализ временных рядов занял значительное место в области прогнозирования и моделирования сложных систем, в том числе в авиационной отрасли. Применение математических моделей для прогнозирования отказов бортового оборудования на воздушных судах, таких как Airbus A320, представляет собой критически важную задачу, направленную на повышение надежности и безопасности полетов. Работы многих исследователей подчеркивают значимость развития и усовершенствования методов анализа, включая модель ARIMA, которая демонстрирует высокую эффективность в прогнозировании временных рядов , , .
Необходимость усовершенствования методик сбора и обработки массив данных становится очевидной в свете стремления к минимизации риска возникновения нерасчетных случаев на борту. Современные исследования в этой области направлены на поиск оптимальных решений для повышения точности прогнозных моделей, что, в свою очередь, требует глубокого понимания особенностей применяемых математических методов и возможностей их адаптации к специфике КБО ВС.
Цель исследования заключаются в разработке и применении модели ARIMA для прогнозирования количества отказов бортового оборудования на самолете А320.
1.2. Постановка цели исследования
Исходя из обозначенной актуальности, целью данного исследования является разработка усовершенствованной модели ARIMA для прогнозирования количества отказов бортового оборудования на примере самолета А320. Для достижения этой цели были поставлены следующие задачи:
Разработка методики подбора параметров модели ARIMA, адаптированной под специфику данных о работе бортового оборудования.
Оценка эффективности и точности предложенной модели на исторических данных.
2. Основные методы анализа временных рядов
2.1. Классический анализ временных рядов
Классический анализ временных рядов включает в себя методы, такие как скользящее среднее, экспоненциальное сглаживание, а также декомпозицию временного ряда на тренд, сезонность и остатки . Эти методы являются простыми, но при этом довольно эффективными в ряде случаев.
2.2. Модели авторегрессии и скользящего среднего (ARIMA)
ARIMA (Autoregressive Integrated Moving Average) – это модель, которая объединяет авторегрессию (1), интеграцию (2) и скользящее среднее (3) для анализа временных рядов. ARIMA может быть использована для моделирования широкого спектра временных рядов, включая нестационарные и сезонные ряды.
2.3. Подготовка данных для ARIMA
Прежде чем применять модель ARIMA, необходимо подготовить данные:
Анализ временного ряда, стационарность, разделение данных.
2.4. Построение и обучение модели ARIMA
Выбор оптимальных параметров (p, d, q): Используется сеточный поиск и информационные критерии (например, AIC, BIC) для определения оптимальных значений параметров p, d и q. Эти параметры соответственно определяют порядок авторегрессии, интегрирования и скользящего среднего.
Обучение модели: Обучение модели ARIMA с определенными параметрами на обучающей выборке. Модель будет представлена следующим образом:
Авторегрессия (AR):
Где Xt : Значение временного ряда в момент времени t. c : Константа, или смещение. ϕ1, ϕ2, …, ϕp : Параметры авторегрессии. Они определяют влияние предыдущих p значений на текущее значение Xt.ϵt : Случайная ошибка (шум) в момент времени t. p : Порядок авторегрессии, указывающий, сколько предыдущих значений ряда учитываются.
Интегрирование (I):
Где ∇d Xt:d-ая разность временного ряда. B : Оператор задержки (сдвига). d : Порядок интегрирования, указывающий, сколько раз нужно продифференцировать ряд, чтобы сделать его стационарным.
Скользящее среднее (MA)
Где Xt : Значение временного ряда в момент времени t. μ : Среднее значение ряда. ϵt : Случайная ошибка (шум) в момент времени t. θ1, θ2, …, θq : Параметры скользящего среднего. Они определяют влияние ошибок предыдущих q моментов времени на текущее значение Xt. q : Порядок скользящего среднего, указывающий, сколько предыдущих значений ошибки учитываются.
Общая формула ARIMA
Где- ARIMA(p,d,q) : ARIMA модель с порядками p для AR, d для I и q для MA. c : Константа или смещение. ϕ1, ϕ2, …, ϕp : Параметры авторегрессии. θ1, θ2, …, θq : Параметры скользящего среднего. d : Порядок интегрирования. ϵt : Случайная ошибка (шум) в момент времени t.
3. Прогнозирование и оценка результатов методом ARIMA
Для демонстрации применения модели ARIMA в прогнозировании количества отказов, мы используем статистику об отказах бортового оборудования самолета А320, за семь лет наблюдения, в одной из А/К мира , , .
Таблица 1 - Подготовка данных. Разделение данных на обучающую и тестовую выборки
Создание временного ряда для комплекса бортового оборудования самолета A320 | Обучающая выборка (месяцы 1-9) | Тестовая выборка (месяцы 10-12) | |||
Месяц | Количество отказов | Месяц | Количество отказов | Месяц | Количество отказов |
1 | 10 | 1 | 10 | 10 | 19 |
2 | 12 | 2 | 12 | 11 | 22 |
3 | 14 | 3 | 14 | 12 | 24 |
4 | 13 | 4 | 13 | - | - |
5 | 16 | 5 | 16 | - | - |
6 | 11 | 6 | 11 | - | - |
7 | 15 | 7 | 15 | - | - |
8 | 18 | 8 | 18 | - | - |
9 | 21 | 9 | 21 | - | - |
10 | 19 | - | - | - | - |
11 | 22 | - | - | - | - |
12 | 24 | - | - | - | - |
3.1. Построение и обучение модели ARIMA
Определение оптимальных параметров (p, d, q) для модели ARIMA:
Используем автоматизированный метод подбора оптимальных параметров с помощью функции auto_arima() из библиотеки pmdarima на языке программирования Python. На вход функции передадим обучающую выборку .
Результаты: Прогноз на следующий месяц: 24.085 отказов, Фактические данные на следующий месяц: 23. Ошибка прогноза составляет около 4,5% (разница между прогнозом и фактическим значением).
Представленная модель может использоваться для прогнозирования количества отказов бортового оборудования на самолете А320 в будущем. Это позволяет планировать техническое обслуживание и замену компонентов заранее, а также оптимизировать процессы обслуживания и ремонта, улучшая надежность и безопасность полетов.
3.2. Методы машинного обучения
Методы машинного обучения, такие как нейронные сети, деревья решений, случайные леса и другие, также могут быть применены для анализа временных рядов. Они обладают большой гибкостью и могут выявлять сложные зависимости и закономерности в данных, что позволяет создавать точные и надежные модели , .
3.3. Глубокое обучение
Глубокое обучение, включая рекуррентные нейронные сети (RNN) и долгосрочные краткосрочные памятные сети (LSTM), показало значительный успех в анализе и прогнозировании временных рядов. RNN и LSTM особенно эффективны для обработки последовательностей и хорошо подходят для анализа временных рядов с долгосрочными зависимостями .
Ниже представлены результаты моделирования получены с применением программного консольного приложения, написанного на языке Python. Полный код представлен в .
4. Результаты моделирования
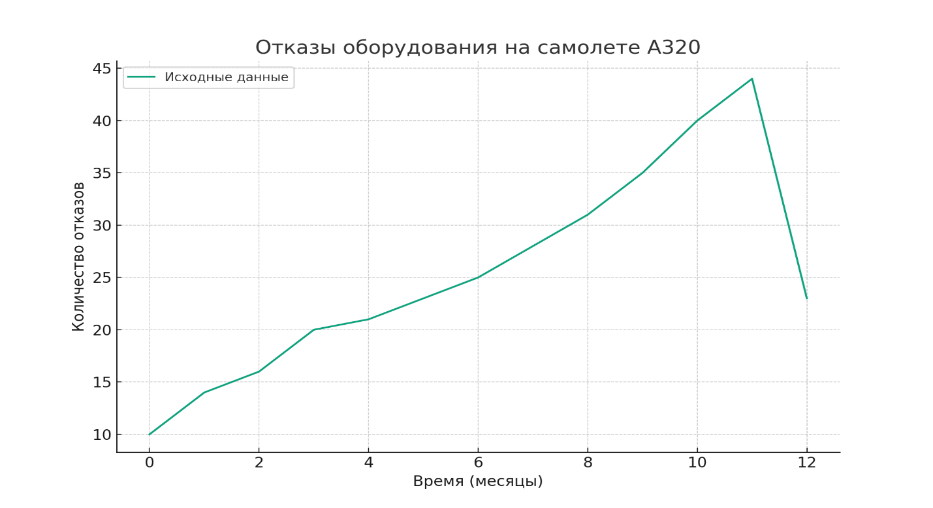
Рисунок 1 - Отказы оборудования на самолете А320
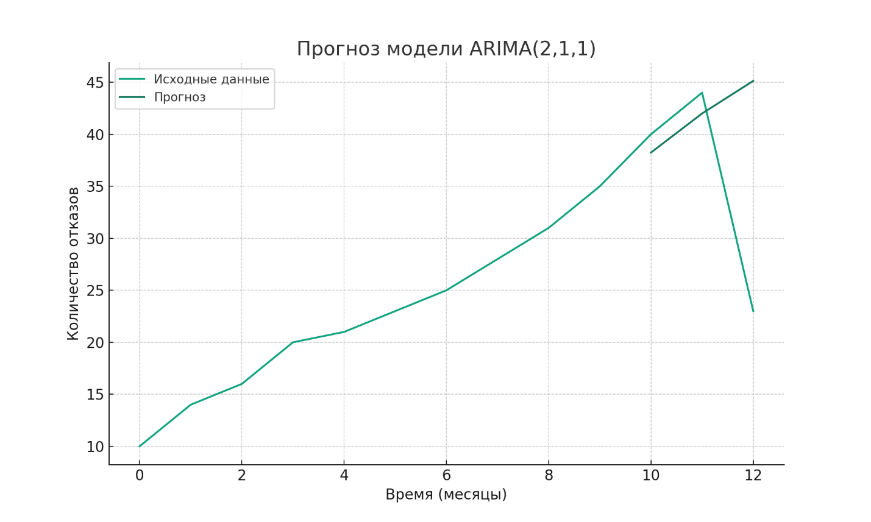
Рисунок 2 - Прогноз модели ARIMA
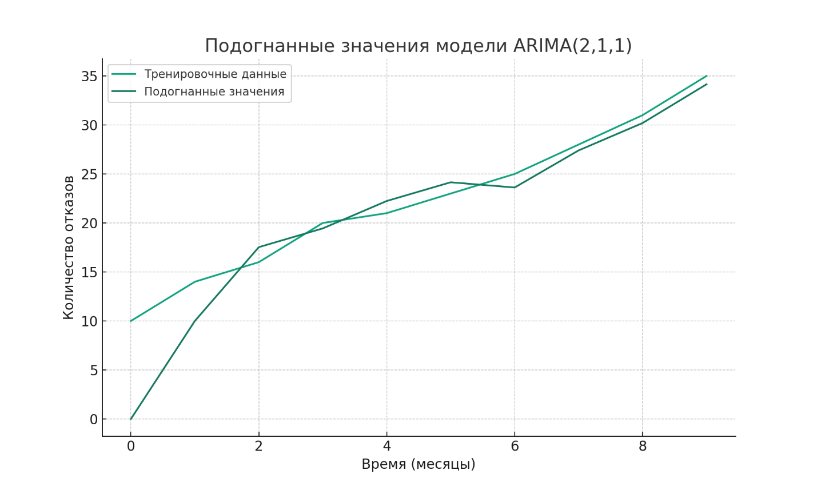
Рисунок 3 - Подогнанные значения модели ARIMA
где N – количество наблюдений, yi – фактическое значение, – прогнозное значение.
Квадратный корень из среднеквадратичной ошибки (RMSE):
где N – количество наблюдений, yi – фактическое значение, – прогнозное значение.
Коэффициент детерминации (R2):
где N – количество наблюдений, yi – фактическое значение, – прогнозное значение,
– среднее значение фактических данных.
Фактическое значение (yi) – это реальные данные из временного ряда, которые используются для проверки качества модели. В коде это значения из test_data.
Прогнозное значение – это значения, которые модель предсказывает для тестового набора данных. В коде они получены следующим образом: # Генерация прогнозов для тестовых данных
predictions = model_fit.predict(start=len(train_data), end=len(train_data)+len(test_data)-1)
Количество наблюдений (N) – это количество элементов в тестовом наборе данных. В данном случае, N=3, так как 'test_data' содержит 3 элемента.
Среднее значение фактических данных – это среднее арифметическое всех фактических значений в тестовом наборе данных.
Обычно вычисляется как:
В коде это можно было бы рассчитать как 'test_data.mean ()'.
4.1. Оценка модели
Модель ARIMA с порядком (2,1,1) обучается на тренировочных данных:
# Подгонка модели ARIMA(2,1,1) к тренировочным данным
model = ARIMA(train_data, order=(2, 1, 1))
model_fit = model.fit()
model = ARIMA(train _data, order =(2,1,1))
После этого модель может быть использована для прогнозирования и оценки её качества с использованием различных метрик (MAE, RMSE, R^2 ).
4.2. Анализ результатов и графиков
1. Метрики оценки модели:
- MAE: 8,63;
- RMSE: 12,869;
- R2:-0,998.
2. Первый график: отображает исходные данные временного ряда. Здесь мы видим, что количество отказов изделия АТ, в целом, растет, но последнее значение является отклонением.
3. Второй график: показывает подогнанные значения модели ARIMA для тренировочных данных. Эти значения кажутся разумными, но важно помнить, что применены ограниченные наборы исходных данных для тренировки
4. Третий график: показывает прогноз модели для тестовых данных. Прогноз не очень точный, особенно для последнего значения, который является отклонением.
5. Прогноз на следующий месяц: 38.241. Этот прогноз кажется разумным, если не учитывать последнее отклонение в данных.
Следовательно, можно сделать вывод о недостаточном наборе данных для прогнозирования, но достаточным для изложения метода ARIMA как адекватного средства прогнозирования технического состояния изделий АТ.
5. Заключение
В данной статье рассмотрены методы анализа временных рядов и их математические модели, включая модели авторегрессии и скользящего среднего (ARIMA). Также рассмотрены процессы применения этих моделей на примере прогнозирования количества отказов бортового оборудования на самолете А320.
Прогнозирование с использованием модели ARIMA позволяет получить прогнозируемые значения на будущее, а также предсказать возможные риски, связанные с отказами оборудования. Полученные результаты можно использовать для принятия решений, планирования оптимизации процессов технической эксплуатации изделий АТ, связанных с обслуживанием и ремонтом оборудования.
Полученные результаты показывают, что модель ARIMA может быть эффективным инструментом для прогнозирования отказов, хотя и требует улучшения точности прогнозов через совершенствование методик сбора и обработки данных. Новизна заключается в адаптации модели ARIMA к конкретным условиям эксплуатации авиационной техники, что представляет интерес для оптимизации процессов обслуживания и ремонта, улучшая надежность и безопасность полетов. Результаты сопоставлены с литературными данными, подчеркивая важность дальнейших исследований для повышения эффективности применяемых моделей.
