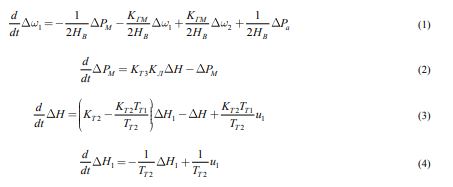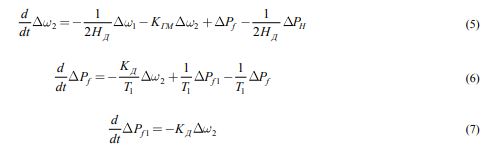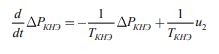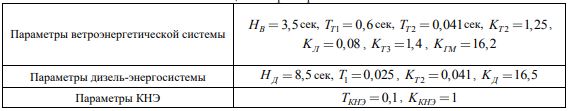ПРОЕКТИРОВАНИЕ РОБАСТНОГО КОНТРОЛЛЕРА ИЗОЛИРОВАННОЙ ВЕТРО-ДИЗЕЛЬНОЙ ЭНЕРГОСИСТЕМЫ С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ КИНЕТИЧЕСКОГО НАКОПЛЕНИЯ ЭНЕРГИИ

ПРОЕКТИРОВАНИЕ РОБАСТНОГО КОНТРОЛЛЕРА ИЗОЛИРОВАННОЙ ВЕТРО-ДИЗЕЛЬНОЙ ЭНЕРГОСИСТЕМЫ С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ КИНЕТИЧЕСКОГО НАКОПЛЕНИЯ ЭНЕРГИИ

Научная статья

Ким Кум Чол^{1, *}, Силин Н.В.²

¹ ORCID: 0000-0002-6622-2040;

² ORCID: 0000-0003-0076-8880;

^{1, 2} Дальневосточный федеральный университет, Владивосток, Россия

* Корреспондирующий автор (kim.kch[at]mail.ru)

Аннотация

Рассмотрены вопросы проектирования робастного контроллера путем введения в изолированную ветро-дизельную энергосистему устройства кинетического накопления энергии. В качестве накопителя используется маховик, обладающий быстрым откликом. Робастный контроллер разработан с использованием теории обратной связи (QFT), позволяющей моделировать неопределенности системы на этапе проектирования контроллера. Проверка эффективности управления робастным контроллером выполнена с помощью динамического моделирования с учетом реальных возмущений при различных условиях эксплуатации. Показано, что предложенный робастный контроллер целесообразно использовать для улучшения динамических характеристик ветро-дизельной энергосистемы.

Ключевые слова: локальная энергосистема, возобновляемые источники энергии, изолированная ветро-дизельная энергосистема, кинетический накопитель энергии, маховик, робастный контроллер, количественная теория обратной связи.

DESIGN OF A ROBUST CONTROLLER OF AN ISOLATED WIND-DIESEL POWER SYSTEM USING A KINETIC ENERGY STORAGE SYSTEM

Research article

Kim Kum Chol ^{1, *}, Silin N.V.²

¹ ORCID: 0000-0002-6622-2040;

² ORCID: 0000-0003-0076-8880;

^{1, 2} Far Eastern Federal University, Vladivostok, Russia

* Corresponding author (kim.kch[at]mail.ru)

Abstract

The study explores the issues of designing a robust controller by introducing a kinetic energy storage device into an isolated wind-diesel power system. A flywheel with a fast response is used as a storage device. The robust controller is designed using quantitative feedback theory (QFT), which allows for modeling the uncertainties of the system at the design stage of the controller. The control efficiency of the robust controller is checked using dynamic modeling taking into account real disturbances under various operating conditions. It is shown that the proposed robust controller can be used to improve the dynamic characteristics of the wind-diesel power system.

Keywords: local power system, renewable energy sources, isolated wind-diesel power system, kinetic energy storage, flywheel, robust controller, quantitative feedback theory.

Введение

Дефицит электроэнергии для потребителей, удаленных от централизованной энергосистемы, в основном компенсируется за счет использования автономных энергетических установок (АЭУ) [1], [2].

Основными требованиями при выборе типа генерирующего оборудования для АЭУ являются бездефицитность, низкая стоимость энергетических ресурсов и экологическая чистота. В наибольшей степени этим требованиям удовлетворяют АЭУ с использованием возобновляемых источников энергии (ВИЭ, прежде всего ветра и солнца) [3].

В мире применяют различные схемы АЭУ на основе ВИЭ. Для зон децентрализованного электроснабжения особый интерес представляют автономные гибридные энергетические установки (АГЭУ), включающие одновременно несколько типов источников энергии – ветроэлектрическую установку (ВЭУ), фотоэлектрические панели (ФЭП), дизельгенераторную установку (ДГУ) и накопители энергии (НЭ). В настоящее время проводится множество исследований по вопросам эффективного использования ветро-дизельных гибридных систем генерации [4].

Существующие в настоящее время технологии пока не позволяют достичь устойчивой работы энергосистем, полностью построенных на использовании возобновляемых источников энергии. В первую очередь это касается поддержания показателей качества электроэнергии по напряжению и частоте.

Для предотвращения колебания частоты используют методы управления ветро-дизельных систем в совокупности с различными методами управления тангажом. В частности, были предложены различные методы, такие как ПИ-регулирование, управление переменной структурой (VSC:VariableStructureControl), нечеткое управление, H∞-управление, с помощью которых проведены исследования частотного регулирования ветро-дизельных систем [5], [6].

Практика показывает, что частотное регулирование имеет существенные ограничения в управлении из-за медленного отклика генератора. Решение этой проблемы возможно путем использования устройства накопления энергии с высокой скоростью отклика ввода / вывода [7]. В частности, достаточно быстрая скорость реакции ввода / вывода активной мощности маховика у кинетического накопителя энергии позволяет эффективно управлять частотой в ответ на внезапные изменения нагрузки и нерегулярную генерацию ветровой энергии [8].

В статье предлагается способ использования системы кинетического накопления энергии (КНЭ) с маховиком для достаточно быстрого управления частотой ветро-дизельной энергосистемы. Для реализации этого способа разработан контроллер, позволяющий отображать с помощью теории робастного управления QFT (QuantitativeFeedbackTheory) характеристики управления с учетом ошибок моделирования системы и различных возмущений. Преимущество проектирования с помощью QFT состоит в том, что появляется возможность разработать робастный контроллер так, чтобы он мог стабильно работать в различных режимах, установив диапазон неопределенности параметра ошибки моделирования системы на этапе проектирования [9], [10], [11].

Для оценки качества работы контроллера, разработанного предложенным методом, выполнено моделирование динамических характеристик во временной области. Результаты исследования, полученные путем моделирования процессов при различных возмущениях, подтвердили, что предложенный контроллер продемонстрировал достаточно хорошие характеристики управления, несмотря на минимизацию величины изменения генератора за счет быстрых характеристик ввода / вывода устройства накопления энергии.

Модель ветро-дизельной энергосистемы

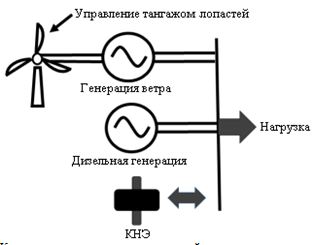
Блок-схема ветро-дизельной энергосистемы, включая КНЭ, представлена на рис. 1. Устройства для генерации энергии ветра, дизельного топлива и КНЭ подключены к одной шине и скомпонованы в конструкцию, которая может подавать питание на нагрузку. Предполагается, что ветрогенератор в основном выполняет управление тангажом лопастей и только активная мощность КНЭ контролируется для регулирования частоты.

Рис. 1 – Компоновочная схема ветро-дизельной энергосистемы, включая КНЭ

Процессы, отображающие динамические характеристики ветроэнергетической системы, включая управление тангажом лопастей ветроколеса, описываются с помощью следующих уравнений (1) – (4) [5], [6], [7]:

где Dw₁– отклонение угловой скорости ветроколеса;

DP_m– отклонение механической мощности на валу ветрогенератора;

Dw2– отклонение угловой скорости дизель-генератора;

DPa– изменение аэродинамической мощности;

H_b– постоянная инерции ветрколеса;

К_ГМ– коэффициент усиления гидромуфты;

К_ТЗ– коэффициент усиления отклика на тангаж подгонки данных;

К_Л– коэффициент усиления характеристики лопастей;

DH– переменная гидравлического привода тангажа;

К_Т² – коэффициент усиления гидравлического привода тангажа;

 T_Т¹    T_Т^2– постоянная времени гидравлического привода тангажа;

DH₁– переменная состояния;

u₁– управляющее воздействие.

Модель динамических характеристик дизельного генератора, включая регулятор, представлена в уравнениях (5) – (7) [5], [6], [7]:

где Н_Д– постоянная инерции дизель-генератора;

DP_f– отклонение мощности дизель-генератора;

DP_H – изменение нагрузки;

K_Д– коэффициент усиления регулятора дизель-генератора;

Т₁– постоянная времени регулятора дизель-генератора;

D P_f1– переменная состояния.

Система кинетического накопления энергии может быть смоделирована с помощью передаточной функции первого порядка, а её выходная мощность представлена в виде следующего уравнения [7]:

где DP_КНЭ – изменение мощности КНЭ;

T_КНЭ – постоянная времени КНЭ;

u₂– управляющее воздействие

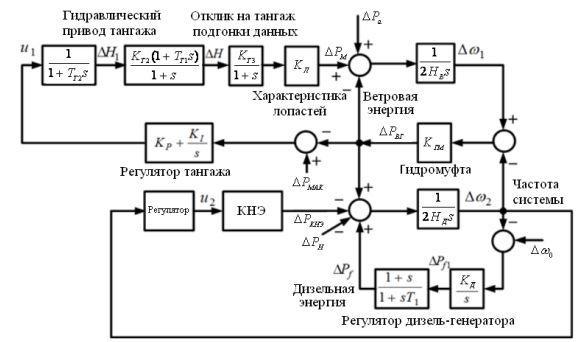
На рис. 2 показана блок-схема модели ветро-дизельной энергосистемы, описываемой уравнениями (1)–(8), включающая в себя модели ветроэнергетической системы, дизельной системы и управления тангажом лопастей.

Рис. 2 – Блок-схема модели передаточной функции ветро-дизельной энергосистемы, включая КНЭ

Модель линеаризации ветроэнергетической системы может быть выражена следующим уравнением:

(9)

где Dx, Du,Dp – вектор состояния, управления и возмущения соответственно;

А, В, Г– постоянные матрицы, зависящие от параметров системы и рабочей точки.

Векторы состояния, управления и возмущения без контроллера следующие:

Проектирование контроллера КНЭ с использованием QFT

Теория управления QFT — это метод проектирования робастного контроллера в частотной области с использованием диаграммы Николса для обеспечения робастного управления с учетом неопределенностей и помех, существующих на определенном объекте. Основная цель использования QFT — обеспечить разработку контроллера с минимальной полосой пропускания, удовлетворяющего при этом заданным характеристикам производительности для объекта, в котором существуют внешние возмущения и неопределенности. Основной метод проектирования заключается в следующем. Учитывая проектную спецификацию объекта с обратной связью и спецификацию неопределенности, система преобразуется в робастную границу устойчивости и робастную границу производительности передаточной функции без обратной связи номинальной системы. Затем контроллер разрабатывается с использованием метода формирования контура для удовлетворения граничного условия, как показано на рис. 3.

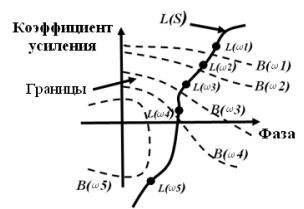Рис. 3 – Оптимальные результаты проектирования при наихудших граничных условиях QFT

Основные этапы проектирования состоят в следующем:

(а) Создание шаблона установки. Для этого разрабатывается набор моделей  для ряда частотных областей, выбранных для целевой модели управления, включая неопределенность.

(б) Определение границы QFT. Выбирается номинальная модель, которая формируется путем выбора базового рабочего значения системы из набора моделей. Запас устойчивости и граница производительности для номинальной модели рассчитываются путем объединения спецификации робастной устойчивости и спецификации производительности шаблона для каждой частоты. Затем в качестве границы QFT выбирается наихудшая граница для каждой частоты.

(в) Формирование контура контроллера QFT. На всех выбранных частотах QFT-регулятор  рассчитывается по диаграмме Николса с использованием метода формирования петель до тех пор, пока не будет выполнено граничное условие QFT и не будет стабилизирована номинальная замкнутая система. В этом случае, если номинальная передаточная функция разомкнутого контура  удовлетворяет границе QFT для наихудшего случая, как показано на рис. 3, на каждой выбранной частоте достигается оптимальная конструкция.

В данной статье QFT-контроллер КНЭ разработан с использованием модели линеаризации ветро-дизельной энергосистемы. Чтобы спроектировать контроллер QFT, сначала необходимо выбрать передаточную функцию системы  для входа и выхода системы, включая КНЭ. Для формирования обратной связи системы выбирается частота дизель-генератора , а полученная передаточная функция определяется как .

Передаточная функция ветро-дизельной энергосистемы  изменяется в соответствии с параметрами неопределенности дизельной и ветровой энергосистем. Предполагая, что коэффициент инерции ветроэнергетической системы , коэффициент инерции дизельной системы  и постоянная времени регулятора  являются неопределенными факторами и каждый параметр отличается на 30% от номинального значения, вышеперечисленные величины ограничены в следующих пределах:

Для выбранного диапазона соотношений (10) – (12) формируется набор передаточных функций, включающий неопределенность передаточной функции системы. Для набора передаточных функций, включающих неопределенность параметра, следует установить интересующую частотную область, которая оказывает большое влияние на систему. Набор частотных областей, выбранных в исследовании, представлен следующими значениями:

Далее следует получить шаблон установки для интересующей частоты, выбранной в уравнении, и создать номинальную модель (см. таблицу 1). После создания номинальной модели следует выбрать спецификации робастной стабильности и подавления возмущений для расчета границы QFT. Спецификации робастной стабильности и подавления возмущений, используемые в исследовании, были выбраны в соответствии со следующими уравнениями [8]:

где K(jw)P(jw)=L(jw) – передаточная функция разомкнутого контура; K(jw)– передаточная функция разработанного контроллера.

Граница QFT вычисляется с использованием численного алгоритма в виде квадратичного неравенства, а не пассивного расчета, как на диаграмме Николса. Передаточная функция разомкнутого контура L(s), удовлетворяющая границе, была получена с использованием метода формирования петель. Если эта передаточная функция удовлетворяет границам QFT на всех выбранных частотах, то появляется возможность построить контроллер КНЭ с передаточной функцией K(s).

Основные результаты и обсуждение

В Таблице 1 приведены параметры дизель-энергосистемы и ветроэнергетической системы, использованные в исследовании.

Таблица 1 – Параметры системы

Передаточная функция разработанного контроллера КНЭ имеет следующий вид:

(16)

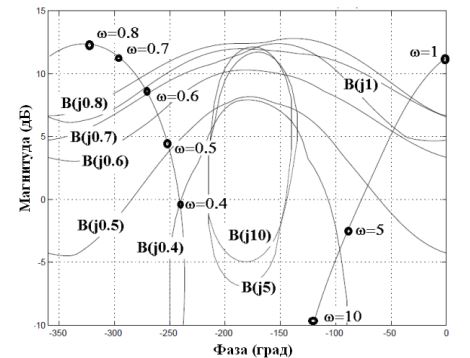
На рис. 4 показаны граничная и номинальная передаточные функции разомкнутой системы , рассчитанные для шаблона системы в соответствии с выбранной частотой . Из рисунка, видно, что  номинальной разомкнутой системы на всех выбранных частотах  удовлетворяет всем граничным условиям QFT.

Рис. 4 – Границы QFT и расчетные результаты формирования петель

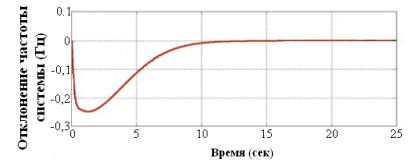
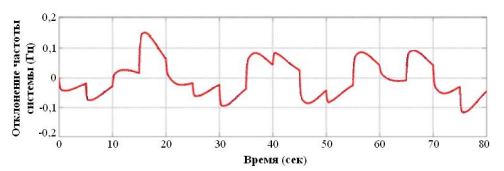
На рис. 5 показан результат изменения частоты ветро-дизельной энергосистемы при применении QFT-регулятора предлагаемого КНЭ при ступенчатом изменении  с шагом  в результате внезапного возмущения нагрузки в дизельной энергосистеме. Применении регулятора позволяет эффективно подавлять отклонение частоты в течение 10 секунд, максимальное отклонение частоты также достаточно мало и составляет -0,246 Гц.

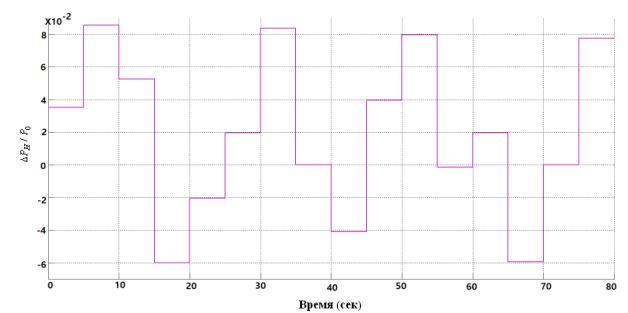
Рис. 5 – Частотная характеристика при изменении DP_H с шагом 0,1 P₀

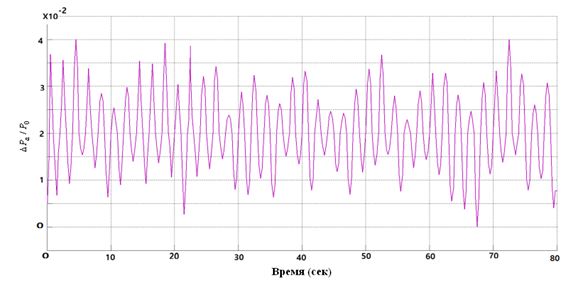
Рис. 6 – Случайное изменение нагрузки DP_H

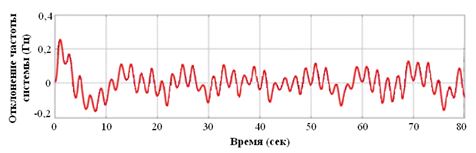
Рисунок 7 демонстрирует результат изменения частоты ветро-дизельной энергосистемы при применении QFT-регулятора для случая, когда  изменяется во времени случайным образом (см. рисунок 6). Отклонение частоты составляет [-0,12, 0,15], что указывает на то, что колебания частоты эффективно подавляются, а эффективность управления является робастной.

Рис. 7 – Частотная характеристика при случайном изменении нагрузки

Рис. 8 – Случайное изменение ветровой энергии

На рис. 9 показан результат изменения частоты ветро-дизельной энергосистемы при работе контроллера в том случае, когда входная мощность ветра  изменяется случайным образом, как показано на рис. 8. В этом случае, отклонение частоты составляет [-0,16, 0,26], что также указывает на эффективность управления.

Рис. 9 – Частотные характеристики при случайном изменении ветровой мощности

Заключение

Для достижения робастного управления ветро-дизельной энергосистемой целесообразно использование КНЭ с контроллером, разработанным на базе QFT. Исследование динамических характеристик КНЭ показывает достаточно эффективное регулирование частоты при изменении нагрузки в широком диапазоне. Результаты моделирования подтверждают, что применение метода контроля устойчивости QFT обеспечивает устойчивость к различным возмущениям и в значительной степени способствует повышению устойчивости ветроэнергетической системы. В частности, было подтверждено, что благодаря применению КНЭ мощность быстро регулировалась при несоответствии между входной и выходной мощностью.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Синявский Ю.В. Интеллектуальный алгоритм управления автономными комплексными энергетическими установками арктического исполнения / Ю.В. Синявский, Е.А. Кириллова //Прикладная информатика. – 2021. – № 4. – С. 74–82.
2. Петров Ю.С. Математические модели электрической системы использования возобновляемых источников энергии для автомного энергоснабжения объектов / Ю.С. Петров, А.К. Музаев //Международный научно-исследовательский журнал. – 2021. – № 9. – С. 33–40.
3. Ковалев К.Л. Автономные энергетические системы с кинетическим накопителем энергии / К.Л. Ковалев, В.Н. Полтавец, И.П. Колчанова // Электричество. – 2019. – № 9. – С. 30–40.
4. Ochoa D. Modeling an Isolated hybrid wind-diesel power system for performing frequency control studies. A case of study: San Cristobal Island, Galapagos–Ecuador / D. Ochoa, S. Martinez // IEEE Latin America Transactions. – 2019. – V. 17. – I. 5. – P. 775–787.
5. Tripathy S. C. Dynamic performance of wind-diesel power system with capacitive energy storage / S. C. Tripathy, I. P. Mishra // Energy Convers.Mgmt. – 1996. – V. 37. – I. 12. – P. 1787–1798.
6. Dasa. D. Dynamics of diesel and wind turbine generators on an isolated power system / D. Dasa, S.K. Adityaa, D.P. Kothari // Electrical Power and Energy Systems. – 1999. – V. 21. – P. 183–189.
7. Thameem Ansari M. Md. Design of dual mode linguistic hedge fuzzy logic controller for an Isolated wind-diesel hybrid power system with lossy magnetic energy storage Unit / M. Md. Thameem Ansari, S.Velusami // Wind engineering. – 2009. – V. 33. – I. 6. – P. 607–629.
8. Полтавец В.Н. Кинетические накопители энергии и их применение в электроэнергетике / В.Н. Полтавец, И.П. Колчанова // Энергобезопасность и энергосбережение. – 2021. – № 6. – С. 26–34.
9. Yacine Dailia. Quantitative feedback theory design of robust MPPT controller for small wind energy conversion systems: Design, analysis and experimental study / Yacine Dailia, Jean-Paul Gaubertb, Lazhar Rahmania, Abdelghani Harragc // Sustainable Energy Technologies and Assessments. – 2019. – V. 35. – P. 308–320.
10. Горовиц, И. Обзор теории количественной обратной связи (QFT) / И. Горовиц // Международный журнал управления. – 1991. – № 2 (53). – С. 255–291.
11. Han K. S. Damping of low frequency oscillation in power system using QFT FESS controller / K. S. Han, M. G. Jeong, , J. P. Lee // Journal of Engineering Research and Application. – 2018. – V. 8. – I. 4. – P. 28–33.
12. Garcia-Sanz M. Wind energy systems: control engineering design / M. Garcia-Sanz, C. H. Houpis. A CRC Press book. Taylor & Francis. 2012. – 613 p.
13. Abedini A. Dynamic model and control of a wind-turbine generator with energy storage / A. Abedini, H. Nikkhajoei // IET Renew. Power Gener. – 2011. – V. 5. – I. 1. – P. 67–78.

Список литературы на английском языке / References in English

1. Sinyavsky Yu.V. Intellektual'nyj algoritm upravlenija avtonomnymi kompleksnymi jenergeticheskimi ustanovkami arkticheskogo ispolnenija [Intelligent control algorithm for autonomous integrated power plants for arctic regions] / Yu.V. Sinyavsky, E.A. Kirillova // Prikladnaja informatika [Applied Informatics]. – 2021. – No. 4. – P. 74–82. [in Russian]
2. Petrov Yu.S. Matematicheskie modeli jelektricheskoj sistemy ispol'zovanija vozobnovljaemyh istochnikov jenergii dlja avtomnogo jenergosnabzhenija ob’ektov [Mathematical models of the electric system for the use of renewable energy sources for autonomous power supply of facilities] / Yu.S. Petrov, A.K. Muzaev // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. – 2021. – No. 9. – P. 33–40. [in Russian]
3. Kovalev K.L. Avtonomnye jenergeticheskie sistemy s kineticheskim nakopitelem jenergii [Autonomous energy systems with kinetic energy storage] / K.L. Kovalev, V.N. Poltavets, I.P. Kolchanova // Jelektrichestvo [Electricity]. – 2019. – № 9. – P. 30–40. [in Russian]
4. Ochoa D. Modeling an Isolated hybrid wind-diesel power system for performing frequency control studies. A case of study: San Cristobal Island, Galapagos–Ecuador / D. Ochoa, S. Martinez // IEEE Latin America Transactions. – 2019. – V. 17. – I. 5. – P. 775–787.
5. Tripathy S. C. Dynamic performance of wind-diesel power system with capacitive energy storage / S. C. Tripathy, I. P. Mishra // Energy Convers.Mgmt. – 1996. – V. 37. – I. 12. – P. 1787–1798.
6. Dasa. D. Dynamics of diesel and wind turbine generators on an isolated power system / D. Dasa, S.K. Adityaa, D.P. Kothari // Electrical Power and Energy Systems. – 1999. – V. 21. – P. 183–189.
7. Thameem Ansari M. Md. Design of dual mode linguistic hedge fuzzy logic controller for an Isolated wind-diesel hybrid power system with lossy magnetic energy storage Unit / M. Md. Thameem Ansari, S.Velusami // Wind engineering. – 2009. – V. 33. – I. 6. – P. 607–629.
8. Poltavets V.N. Kineticheskie nakopiteli jenergii i ih primenenie v jelektrojenergetike [Flywheel energy storage systems and their applications in power engineering] / V.N. Poltavets, I.P. Kolchanova // Jenergobezopasnost' i jenergosberezhenie [Energy safety and energy saving]. – 2021. – No. 6. – P. 26–34. [in Russian]
9. Yacine Dailia. Quantitative feedback theory design of robust MPPT controller for small wind energy conversion systems: Design, analysis and experimental study / Yacine Dailia, Jean-Paul Gaubertb, Lazhar Rahmania, Abdelghani Harragc // Sustainable Energy Technologies and Assessments. – 2019. – V. 35. – P. 308–320.
10. Horowitz, I. Obzor teorii kolichestvennoj obratnoj svjazi (QFT) [A review of the theory of quantitative feedback (QFT)] / I. Horowitz // Mezhdunarodnyj zhurnal upravlenija [International Journal of Management]. – 1991. – No. 2 (53). – P. 255–291. [in Russian]
11. Han K. S. Damping of low frequency oscillation in power system using QFT FESS controller / K. S. Han, M. G. Jeong, , J. P. Lee // Journal of Engineering Research and Application. – 2018. – V. 8. – I. 4. – P. 28–33.
12. Garcia-Sanz M. Wind energy systems: control engineering design / M. Garcia-Sanz, C. H. Houpis. A CRC Press book. Taylor & Francis. 2012. – 613 p.
13. Abedini A. Dynamic model and control of a wind-turbine generator with energy storage / A. Abedini, H. Nikkhajoei // IET Renew. PowerGener. – 2011. – V. 5. – I. 1. – P. 67–78.