НИЗКОЧАСТОТНЫЙ МАГНИТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ В ДВУХСЛОЙНОЙ МАГНИТОСТРИКЦИОННО-ПЬЕЗОЭЛЕКТРИЧЕСКОЙ СТРУКТУРЕ

НИЗКОЧАСТОТНЫЙ МАГНИТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ В ДВУХСЛОЙНОЙ МАГНИТОСТРИКЦИОННО-ПЬЕЗОЭЛЕКТРИЧЕСКОЙ СТРУКТУРЕ

Научная статья

Филиппов Д.А.^1, *, Лалетин В.М.², Поддубная Н.Н.³, Никитин Е.И.⁴, Кузнецов Н.П.⁵

¹ ORCID: 0000-0002-4359-7770;

² ORCID: 0000-0002-3531-0629;

³ ORCID: 0000-0002-9809-487X;

⁴ ORCID: 0000-0003-0718-3682;

⁵ ORCID :0000-0002-6637-5513;

^{1, 4, 5} Новгородский государственный университет имени Ярослава Мудрого, Великий Новгород, Россия;

^{2, 3} Институт технической акустики, Витебск, Белоруссия

* Корреспондирующий автор (Dmitry.Filippov[at]novsu.ru)

Аннотация

Представлена теория магнитоэлектрического эффекта в двухслойной магнитострикционно-пьезоэлектрической структуре магнетик – пьезоэлектрик в низкочастотной области спектра. На основе решения уравнений теории упругости и электростатики получено простое выражение для магнитоэлектрического коэффициента по напряжению через физические параметры материала и геометрические характеристики структуры. Рассмотрен вклад в величину эффекта, обусловленный изгибными деформациями и планарными деформациями. Показано, что вклад от планарных деформаций в величину эффекта значительно превосходит величину вклада от изгибных деформаций. Приведены результаты расчета для структур никель – ЦТС и пермендюр – ЦТС.

Ключевые слова: композиционные мультиферроики, магнитострикция, пьезоэлектричество, магнитоэлектрический эффект, магнитоэлектрический коэффициент.

LOW-FREQUENCY MAGNETOELECTRIC EFFECT IN A TWO-LAYER MAGNETOSTRICTIVE-PIEZOELECTRIC STRUCTURE

Research article

Filippov D.A.^1, *, Laletin V.M.², Poddubnaya N.N.³, Nikitin E.I.⁴, Kuznetsov N.P.⁵

¹ ORCID: 0000-0002-4359-7770;

² ORCID: 0000-0002-3531-0629;

³ ORCID: 0000-0002-9809-487X;

⁴ ORCID: 0000-0003-0718-3682;

⁵ ORCID :0000-0002-6637-5513;

^{1, 4, 5} Yaroslav-the-Wise Novgorod State University; Veliky Novgorod, Russia;

^{2, 3} Institute of Technical Acoustics; Vitebsk, Belarus

* Corresponding author (Dmitry.Filippov[at]novsu.ru)

Abstract

The study presents a theory of the magnetoelectric effect in a two-layer magnetostrictive and piezoelectric structure of magnetic and piezoelectric materials in the low-frequency region of the spectrum. Based on the solution of the equations of the theory of elasticity and electrostatics, a simple expression for the magnetoelectric stress coefficient is obtained via the physical parameters of the material and the geometric characteristics of the structure. The study examines the contribution to the value of the effect caused by flexion strain and planar deformations. It is shown that the contribution from planar deformations to the value of the effect significantly exceeds the value of the contribution from flexion strains. The authors demonstrate the calculation results for the nickel – lead zirconate titanate and permendur – lead zirconate titanate structures.

Keywords: composite multiferroics, magnetostriction, piezoelectricity, magnetoelectric effect, magnetoelectric coefficient.

Введение

Композиционные слоистые структуры магнетик – пьезоэлектрик обладают лучшими магнитоэлектрическими (МЭ) характеристиками по сравнению с объемными композитами [1], [2], [3]. Одним из важнейших преимуществ таких структур является то, что при их изготовлении возможно использовать непосредственно ферромагнетики, обладающие высокой магнитострикцией, такие как пермендюр, D-Terfenol , галфенол и др., в то время как при изготовлении объемных композитов используют оксиды ферромагнетиков и их соединений, такие как феррит-никелевая, феррит-кобальтовая шпинели и др.[2]. Это связано с тем, что ферромагнетики, как правило, являются хорошими проводниками, и их использование при изготовлении объемных композитов приводит к возникновению больших токов утечки, что ведет к резкому увеличению потерь. При изготовлении слоистых структур слой ферромагнетика хорошо изолирован слоем пьезоэлектрика, в результате чего потерь, связанных с токами утечки не возникает. Ранее теоретически МЭ эффект в двухслойных структурах изучался в работах [4], [6], [10], а в трехслойных – в работах [11], [14], [15]. В работах [4], [7] и [11], [13] исследовался МЭ эффект, обусловленный планарными колебаниями структуры, а в работах [5], [8], [10] и [14], [15] изучался МЭ эффект, обусловленный изгибными деформациями.

Особое внимание в этих работах уделялось области электромеханического резонанса, при котором происходит пиковое увеличение эффекта. Низкочастотной области спектра внимание уделялось чрезвычайно мало, хотя в связи с возрастающим числом исследований, направленных на создание сборщиков энергии – харвесторов на основе МЭ эффекта, эта область чрезвычайно важна. Полученные в работах [5], [9], [10] формулы для величины МЭ эффекта чрезвычайно громоздки и сложны для анализа. Авторы не привели их предельный переход для низкочастотной области спектра и недостаточно проанализировали зависимость величины эффекта от параметров структуры. В данной работе приведена основанная на уравнениях теории упругости и электростатики теория МЭ эффекта в низкочастотной области спектра, получены простые выражения для магнитоэлектрического коэффициента по напряжению через физические параметры материалы и геометрические характеристики структуры. Проанализированы вклады в эффект от планарных и изгибных деформаций и их зависимость от геометрических параметров структуры.

Модель

В качестве модели рассмотрим двухслойную структуру магнетик – пьезоэлектрик, схематичное изображение которой представлено на рис. 1. Начало системы координат совместим с центром образца, а ось X (1) совместим с границей раздела между слоем пьезоэлектрика и слоем магнетика.

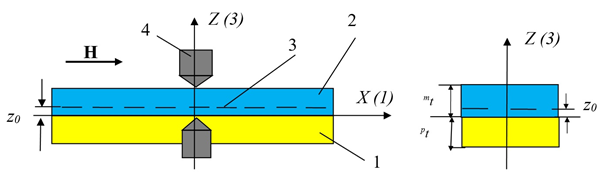
Рис.1 – Схематичное изображение структуры:

1 - p – слой (пьезоэлектрик PZT); 2 – m – слой (магнетик); 3 – нейтральная линия; 4 – электроды

 

В дальнейшем мы будем предполагать, что длина образца много больше его ширины W и толщины . В этом приближении материальные уравнения для пьезоэлектрической и магнитострикционных фаз будут иметь следующий вид:

    (1)

     (2)

    (3)

 

где ,  – компоненты тензора деформаций пьезоэлектрического и магнитострикционного слоев,  – их модули Юнга, ,  – компоненты вектора напряженности электрического поля и электрической индукции, ,– компоненты тензора напряжений пьезоэлектрической и магнитострикционной фаз, ,  – пьезоэлектрический и пьезомагнитные коэффициенты,   – компонента тензора диэлектрической проницаемости пьезоэлектрика.

Метод решения

При нахождении МЭ коэффициента по напряжению будем исходить из того, что при помещении образца в магнитное поле в магнетике, вследствие магнитострикции, возникают деформации растяжения в случае положительной магнитострикции (пермендюр, D-Terfenol) или сжатия в случае, если магнетик обладает отрицательной магнитострикцией (никель, феррит-никелевая шпинель). Посредством механической связи через интерфейс эти деформации передаются в пьезоэлектрическую фазу, в результате чего образец в целом может испытать планарные деформации типа растяжение или сжатие или могут возникнуть деформации изгиба. При нахождении деформаций образца в целом будем исходить из того, что вследствие того, что длина образца много больше его толщины можно считать, что при планарных колебаниях деформации слоев одинаковы, т. Е. считать, что выполняется равенство:

    (4)

Условие равновесия образца, а именно равенство нулю X проекции силы дает следующее уравнение:

     (5)

Выражая из уравнений (1) и (2) компоненты тензора напряжений и подставляя полученные выражения в уравнение (5) получим следующее выражение:

   (6)

Отсюда для планарных деформаций получим выражение в виде:

    (7)

где введены обозначения  - среднее значение модуля Юнга структуры,  - полная толщина образца.

Подставляя полученное выражение в уравнение (3) и используя условие разомкнутой цепи, которое в данном случае принимает вид  для напряженности электрического поля, индуцированной в пьезоэлектрике вследствие планарных деформаций, получим выражение:

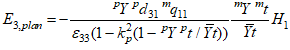    (8)

Используя определение МЭ коэффициента по напряжению (MEVC) в виде , получим для вклада в него от планарных деформаций следующие выражение:

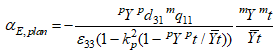    (9)

Как и следовало ожидать, выражение (9) совпадает с выражением для MEVC, полученным в работе [7] при предельном переходе, когда частота магнитного поля стремится к нулю.

В выражении (9) параметр , поэтому данное выражение можно упростить, записав его в виде:

      (10)

Уравнения (9) и (10) позволяют проанализировать зависимость MEVC от физических параметров магнетика и пьезоэлектрика и соотношения толщин их слоев.

При исследовании вклада от деформаций изгиба будем предполагать, что связь между слоями идеальная и, вследствие этого, для деформаций пьезоэлектрика и магнетика имеет место соотношение:

    (11)

где  - координата нейтральной линии,  - радиус кривизны нейтральной линии, который связан с изгибающим моментом соотношением [16]:

   (12)

Здесь введены обозначения:

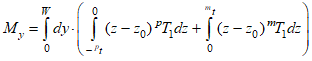 - изгибающий момент, ,  - моменты инерции сечений относительно нейтральной оси , которые, согласно теореме Штейнера, определяются следующими выражениями:

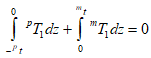    (13)       (14) Положение нейтральной линии определим, следуя теории изгиба, из равенства нулю X -проекции силы, а именно:     (15)

Подставляя в (15) выражения для компонент тензора напряжений  и , полученные из (1) и (2), и полагая внешние воздействия слабыми, для координаты нейтральной линии z₀ получим следующее выражение:

     (16)

В общем случае нейтральный слой может лежать как в пьезоэлектрике, так и в магнетике. Если нейтральный слой расположен в пьезоэлектрике, то в этом случае одна часть пьезоэлектрика, лежащая выше слоя испытывает растяжение (сжатие), другая часть сжатие (растяжение). Возникающие при этом электрические поля в различных частях пьезоэлектрика будут иметь противоположные направления, в результате чего суммарное электрическое поле уменьшится. Если же нейтральный слой расположен в магнетике, то возникающие под действием магнитного поля изгибающие моменты в частях, расположенных по разные стороны от нейтрального слоя, будут иметь противоположные направления, в результате чего суммарный изгибающий момент уменьшается. Оптимальным, с точки зрения получения максимального МЭ отклика, является случай, когда нейтральный слой расположен на границе раздела магнетик – пьезоэлектрик, т. е. когда =0. Это дает оптимальное соотношение между толщинами магнетика и пьезоэлектрика, которые, согласно (16), будет определяться равенством:

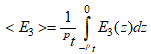    (17) Электрическое поле, возникающее в пьезоэлектрике в результате деформаций изгиба, также найдем из условия разомкнутой цепи, согласно которому получим:     (18) Или, после несложных преобразований, получим:     (19) где  - цилиндрическая жесткость при изгибе. 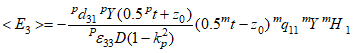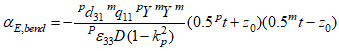Среднее значение напряженности электрического поля определим из соотношения:    (20) Подставляя (19) в (20) и интегрируя, получим:    (21) Используя определение MEVC как  получим для него выражение, связанное с колебаниями изгиба, в виде:     (22)

Уравнение (22) позволяет рассчитывать MEVC, обусловленный возникновением под действием магнитного поля, деформаций изгиба, зная физические параметры материалов композита и геометрические характеристики структуры.

Результаты и обсуждение

МЭ коэффициент по напряжению структуры будет равен сумме вкладов, возникающих от планарных и изгибных деформаций, т. е.:

    (23)

Следует отметить, что эти вклады входят в сумму с противоположными знаками. Это объясняется тем, что при планарных колебаниях деформации, возникающие в магнетике под действием электрического поля, вызывают в пьезоэлектрике деформации того же знака. Например, в случае магнетика с положительной магнитострикцией в магнитострикционном слое возникают деформации растяжения, которые передаваясь через границу раздела вызывают в пьезоэлектрике также деформации растяжения. В случае изгиба деформации растяжения в магнетике вызывают деформации сжатия в пьезоэлектрике, в результате чего возникает электрическое поле, направленное противоположно электрическому полю, вызванному планарными деформациями. Оба этих вклада пропорциональны произведению пьезоэлектрического тензора d на пьезомагнитный тензор q и модуль Юнга пьезоэлектрика ^pY и обратно пропорциональны величины диэлектрической проницаемости диэлектрика ; они не зависят от ширины и длины образца, но по-разному зависят от отношения толщин пьезоэлектрика и магнетика. На рис. 2 представлена зависимость MEVC для структуры никель – ЦТС, а на рис. 3 для структуры пермендюр – ЦТС в зависимости от толщины магнетика при фиксированной толщины пьезоэлектрика. Параметры, используемые для расчетов, представлены в таблице 1.

 

Таблица 1 – Параметры материалов композиционных структур

Материал	Модуль Юнга Y, GPa	Плотность, ρ, kg/m3	Пьезомодули d31, pC/N; q11, ppm/Oe	Диэлектрическая проницаемость e
PZT	66,7	8,2	-175	1750
Ni	215	8,9	-0,06	-
пермендюр	207	8,1	0,1	-

 

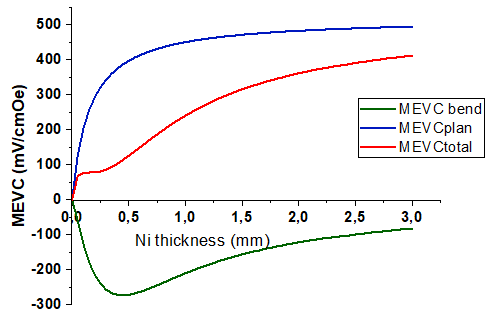
Рис. 2 – Зависимость MEVC от толщины магнетика для структуры никель – ЦТС при толщине пьезоэлектрика ^pt=0.5 mm

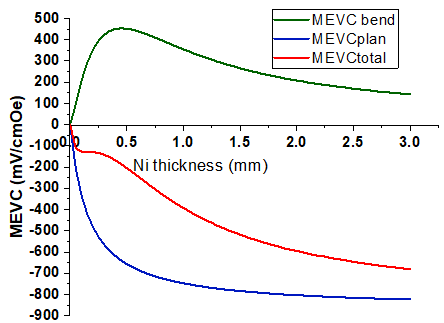
Рис. 3 – Зависимость MEVC от толщины магнетика для структуры пермендюр – ЦТС при толщине пьезоэлектрика ^pt=0.5 mm

Как видно из рисунков, при увеличении толщины магнетика MEVC, обусловленным планарными деформациями, монотонно возрастает и стремится к насыщению при значениях толщины магнетика много большей толщины пьезоэлектрика. Максимальная величина MEVC при насыщении вследствие планарных деформаций, согласно (9), будет определяться соотношением:

    (24)

В отличие от него, MEVC, связанный с деформациями изгиба, сначала возрастает, затем достигает максимума, когда нейтральная линия совпадает с границей раздела магнетик – пьезоэлектрик, а затем убывает. Как уже отмечалось, эти вклады имеют разные знаки, причем вклад от планарных деформаций превосходит вклад от изгибных деформаций во всем диапазоне изменения толщины магнетика. Суммарный MEVC также возрастает с увеличением толщины магнетика, причем в диапазоне, где вклад от изгибных деформаций достигает максимума, рост замедляется и наблюдается небольшое плато. Следует также отметить, что поскольку никель обладает отрицательной магнитострикцией, а пермендюр положительной, то MEVC для структуры никель – ЦТС и никель – пермендюр имеет противоположные знаки.

Заключение

В двухслойных магнитострикционно-пьезоэлектрических структурах магнитоэлектрический эффект связан с планарными деформациями и деформациями изгиба, возникающими при помещении структуры в магнитное поле. Величина вклада в MEVC от планарных деформаций монотонно увеличивается с увеличением толщины магнетика и достигает насыщения при толщинах магнетика много больше толщины пьезоэлектрика. Величина вклада от изгибных деформаций сначала возрастает, затем достигает максимума, когда выполняется соотношение , а затем монотонно стремится к нулю. Вклады от планарных и изгибных деформаций имеют разные знаки, причем вклад от планарных деформаций больше вклада от изгибных деформаций во всем диапазоне изменения толщины магнетика. Суммарный MEVC итоге возрастает с увеличением толщины магнетика и стремится к насыщению при толщине магнетика много большей толщины пьезоэлектрика.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Vopson M. Fundamentals of Multiferroic Materials and Their Possible Applications / M. M. Vopson // Critical Reviews in Solid State and Materials Sciences – 2015 – V.40 –P. 223.
2. Composite Magnetoelectrics: Materials, Structures, and Applications / Eds: G. Srinivasan, S. Priya, and N. X. Sun, Woodhead Publishing Series in Electronic and Optical Materials, No.62, 2015.
3. Srinivasan G. Magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides / G. Srinivasan, E.T. Rasmussen, J. Gallegos et al. // Phys. Rev. B. – 2001 – V. 64 –P. 214408.
4. Филиппов Д. А Теория магнитоэлектрического эффекта в двухслойных ферромагнет-пьезоэлектрических структурах / Д. А Филиппов // Письма в ЖТФ. - 2004. - Т. 30. - № 23. - С. 24-31
5. Филиппов Д. А. Теория магнитоэлектрического эффекта в гибридных феррит-пьезоэлектрических композиционных материалах / Д. А. Филиппов // Письма в ЖТФ – 2004 – т. 30- №9 – с. 6 - 11.
6. Филиппов Д. А Теория магнитоэлектрического эффекта в гетерогенных структурах на основе ферромагнетик – пьезоэлектрик / Д. А. Филиппов // ФТТ. – 2005 - Т. 47 - №6, С.1082-1084.
7. Филиппов Д. А. Магнитоэлектрический эффект в двухслойной магнитострикционно-пьезоэлектрической структуре / Д. А. Филиппов, В. М. Лалетин, T. A. Galichyan // ФТТ – 2013 – т. 55 - №9 – С.1728 -1733.
8. Petrov V. M. Theory of magnetoelectric effect for bending modes in magnetostrictive-piezoelectric bilayers / V. M. Petrov, G. Srinivasan, M. I. Bichurin et al. // J. Appl. Phys. – 2009 – V.105 – P. 063911
9. Бичурин М. И. Изгибные колебания двухслойной магнитострикционно-пьезоэлектрической структуры / М. И. Бичурин, В. М. Петров, К. В. Лаврентьева и др. // Вестник Новгородского государственного университета – 2011. - №65. С. 11-13
10. Sreenivasulu G. Magneto-electric interactions at bending resonance in an asymmetric multiferroic composite: Theory and experiment on the influence of electrode position / Sreenivasulu, P. Qu, V. M. Petrov et al. // J. Appl. Phys. – 2015 – V.117 – P. 174105
11. Филиппов Д. А. Магнитоэлектрический эффект в трехслойной магнитострикционно-пьезоэлектрической структуре / Д. А. Филиппов, Т. А. Галичян // Перспективные материалы – 2013 - №12 - с. 1-6.
12. Филиппов Д. А. Магнитоэлектрический эффект в структуре никель – арсенид галлия – никель / Д. А. Филиппов, Т.О. Фирсова В.М. Лалетин и др. // Письма в ЖТФ – 2017 - т. 43 - вып 6 - с. 72-77.
13. Лалетин В. М. Особенности магнитоэлектрического эффекта в структурах пермендюр – кварц – пермендюр в области электромеханического резонанса / В. М. Лалетин, Д. А. Филиппов, Н. Н. Поддубная и др. // Письма в ЖТФ – 2019 - том 45 - вып. 9 с. 16-18 DOI: 10.21883/PJTF.2019.09.47706.17661
14. Ying Liu Resonance magnetoelectric characteristics of Terfenol-D /Pb(Zr0.52Ti0.48)O3/Ni asymmetric three layered composites / Ying Liu, Chao Yang, Peng Zhou et al. // IOP Conf. Series: Materials Science and Engineering 656 (2019) 012056 IOP Publishing DOI:10.1088/1757-899X/656/1/012056
15. Филиппов Д. А. Магнитоэлектрический эффект в трехслойных асимметричных структурах в области изгибных мод колебаний / Д.А. Филиппов, T.A. Galichyan, J. Zhang и др. // Физика твердого тела, 2020, том 62, вып. 8 с. 1192-1199
16. Дарков А.В. Сопротивление материалов / А.В. Дарков, Г.С. Шпиро. Изд. 4-е. М., Высшая школа. (1975). 654 с.

Список литературы на английском языке / References in English

1. Vopson M. M. Fundamentals of Multiferroic Materials and Their Possible Applications / M. M. Vopson // Critical Reviews in Solid State and Materials Sciences – 2015 – V.40 –P. 223.
2. Composite Magnetoelectrics: Materials, Structures, and Applications / Eds: G. Srinivasan, S. Priya, and N. X. Sun, Woodhead Publishing Series in Electronic and Optical Materials, No.62, 2015.
3. Srinivasan G. Magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides / G. Srinivasan, E.T. Rasmussen, J. Gallegos et al. // Phys. Rev. B. – 2001 – V. 64 –P. 214408.
4. Filippov D.A. Teorija magnitojelektricheskogo jeffekta v dvuhslojnyh ferromagnet-p'ezojelektricheskih strukturah [Theory of magnetoelectric effect in ferromagnetic-piezoelectric bilayer structures] / D.A Filippov // Pis'ma v ZhTF [Technical Physics Letters] – 2004 - Vol. 30 - № 12 - P. 983-986. [in Russian]
5. Filippov D.A. Teorija magnitojelektricheskogo jeffekta v gibridnyh ferrit-p'ezojelektricheskih kompozicionnyh materialah [Theory of magnetoelectric effect in ferrite-piezoelectric hybrid composites] / D.A. Filippov // Pis'ma v ZhTF [ Phys. Lett]. 2004 – V. 30 – p. 351–353 [in Russian]
6. Filippov A. Teorija magnitojelektricheskogo jeffekta v geterogennyh strukturah na osnove ferromagnetik – p'ezojelektrik [Theory of the Magnetoelectric Effect in Ferromagnetic–Piezoelectric Heterostructures] / D.A. Filippov // Physics of the Solid State – 2005 - Vol. 47 - No. 6, pp. 1118–1121. [in Russian]
7. Filippov D. A. Magnitojelektricheskij jeffekt v dvuhslojnoj magnitostrikcionno-p'ezojelektricheskoj strukture [Magnetoelectric Effect in a Magnetostrictive–Piezoelectric Bilayer Structure] / D.A. Filippov, V.M. Laletin, T.A. Galichyan // Physics of the Solid State, 2013, Vol. 55, No. 9, pp. 1840–1845. [in Russian]
8. Petrov V. M. Theory of magnetoelectric effect for bending modes in magnetostrictive-piezoelectric bilayers / V. M. Petrov, G. Srinivasan, M. I. Bichurin et al. // J. Appl. Phys. – 2009 – V.105 – P. 063911
9. Bichurin M.I. Izgibnye kolebanija dvuhslojnoj magnitostrikcionno-p'ezojelektricheskoj struktury [Flexural vibrations of a two-layer magnetostrictive-piezoelectric structure] / M.I. Bichurin, V.M. Petrov, K.V. Lavrent'eva et al. // Vestnik Novgorodskogo gosudarstvennogo universiteta [Vestnik of Novgorod State University] - 2011. - No. 65. P. 11-13. [in Russian]
10. Sreenivasulu G. Magneto-electric interactions at bending resonance in an asymmetric multiferroic composite: Theory and experiment on the influence of electrode position / G. Sreenivasulu, P. Qu, V. M. Petrov et al. // J. Appl. Phys. – 2015 – V.117 – P. 174105
11. Filippov D.A. Magnitojelektricheskij jeffekt v trehslojnoj magnitostrikcionno-p'ezojelektricheskoj strukture [Magnetoelectric effect in a three-layer magnetostrictive-piezoelectric structure] / D.A. Filippov, T.A. Galichjan // Perspektivnye materialy [Perspective materials] - 2013 - №12 - p. 1-6 [in Russian]
12. Filippov D.A. Magnitojelektricheskij jeffekt v strukture nikel' – arsenid gallija – nikel' [The Magnetoelectric Effect in Nickel–Gallium Arsenide–Nickel Structures] / D. A. Filippov, T.O. Firsova V.M. Laletin et al. // Pis'ma v ZhTF [Technical Physics Letters], 2017, Vol. 43, No. 3, pp. 313–315 DOI: 1134/S106378501703018X [in Russian]
13. Laletin V.M. Osobennosti magnitojelektricheskogo jeffekta v strukturah permendjur – kvarc – permendjur v oblasti jelektromehanicheskogo rezonansa [Specific Features of the Magnetoelectric Effect in Permendur–Quartz–Permendur Structures in the Region of Electromechanical Resonance] / V.M. Laletin, D.A. Filippov, N.N. Poddubnaja et al. // Pis'ma v ZhTF [Technical Physics Letters], 2019, Vol. 45, No. 5, pp. 436–438. DOI: 1134/S1063785019050092 [in Russian]
14. Ying Liu Resonance magnetoelectric characteristics of Terfenol-D /Pb(Zr0.52Ti0.48)O3/Ni asymmetric three layered composites / Ying Liu, Chao Yang, Peng Zhou et al. // IOP Conf. Series: Materials Science and Engineering 656 (2019) 012056 IOP Publishing DOI:10.1088/1757-899X/656/1/012056
15. Filippov A. Magnitojelektricheskij jeffekt v trehslojnyh asimmetrichnyh strukturah v oblasti izgibnyh mod kolebanij [Magnetoelectric Effect in Three-Layer Asymmetric Structures in the Region of Bending Vibrational Modes] / D.A. Filippov, T.A. Galichyan, J. Zhang et al. // Fizika tverdogo tela [Physics of the Solid State], 2020, Vol. 62, No. 8, pp. 1338–1345. [in Russian]
16. Darkov A.V. Soprotivlenie materialov [Strength of materials] / A.V. Darkov, G.S. Shpiro Ed. 4th. M., High School. (1975). 654 p.[in Russian]