МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИИ НАНОЧАСТИЦ В ЖИДКОСТИ В ПРОЦЕССЕ ИХ ОСАЖДЕНИЯ. РЕЗУЛЬТАТЫ РАСЧЕТОВ

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИИ НАНОЧАСТИЦ В ЖИДКОСТИ В ПРОЦЕССЕ ИХ ОСАЖДЕНИЯ. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Научная статья

Хуссейн С.М.Р.Х.^1, *, Нуреев И.И.², Данилаев М.П.³, Куклин В.А.⁴, Анфиногентов В.И.⁵, Сахабутдинов А.Ж.⁶, Салахутдинов М.Ш.⁷

¹ ORCID:0000-0001-6022-0548;

² ORCID: 0000-0003-4895-2695;

³ ORCID: 0000-0002-7733-9200;

⁵ ORCID:0000-0003-0015-2429;

⁶ ORCID:0000-0002-0713-7806;

⁷ ORCID: 0000-0001-5176-1334;

¹ Университет Кербелы, Кербела, Ирак;

^2-7 Казанский национальный исследовательский технический университет им. А.Н. Туполева‑КАИ, Казань, Россия;

⁴ Казанский федеральный университет, Казань, Россия

* Корреспондирующий автор (safaa_m333[at]yahoo.com)

Аннотация

В работе приводятся результаты численного моделирования осаждения частиц в растворителе (этилацетате), рассмотрен ряд частных случаев осаждения двух типов частиц (наполнителя – оксид алюминия и полимера) в стационарной и нестационарной жидкости (этилацетате). Исследованы поля температуры и скоростей в жидкости в зависимости от различных способов нагрева внешних границ области с растворителем. Предложен оптимальный выбор метода нагрева для обеспечения равномерного поля скоростей и температуры в окне контроля концентрации. Построена зависимость температуры и скорости восходящего потока в растворителе в зависимости от перепада температур на границах емкости. Произведена серия расчетов движения частиц в нестационарной жидкости.

Ключевые слова: седиментация, математическая модель, осаждение частиц в жидкости, измерение молекулярной массы, измерение наночастиц, измерение концентрации, рассеяние Рэлея, численное интегрирование.

A MATHEMATICAL MODEL FOR MEASURING THE CONCENTRATION OF NANOPARTICLES IN A LIQUID DURING THEIR SETTLING: CALCULATION RESULTS

Research article

Hussein S.M.R.H.^1, *, Nureev I.I.², Danilaev M.P.³, Kuklin V.A.⁴, Anfinogentov V.I.⁵, Sakhabutdinov A.Zh.⁶, Salakhutdinov M.Sh.⁷

¹ ORCID:0000-0001-6022-0548;

² ORCID: 0000-0003-4895-2695;

³ ORCID: 0000-0002-7733-9200;

⁵ ORCID:0000-0003-0015-2429;

⁶ ORCID:0000-0002-0713-7806;

⁷ ORCID: 0000-0001-5176-1334;

¹ University of Karbala, Karbala, Iraq;

^2-7 A.N.Tupolev‑ Kazan National Research Technical University, Kazan, Russia;

⁴ Kazan Federal University, Kazan, Russia

* Corresponding author (safaa_m333[at]yahoo.com)

Abstract

The article presents the results of numerical simulation of particle settling in a solvent (ethyl acetate) and considers a number of special settling cases of two particle types (filler – aluminum oxide and polymer) in a stationary and non-stationary liquid (ethyl acetate). The study investigates the temperature and velocity fields in the liquid depending on different methods of heating the outer boundaries of the region with a solvent. The authors of the study propose the optimal choice of the heating method to ensure a uniform velocity and temperature field in the concentration control window and constructs the dependence of the temperature and the velocity of the ascending flow in the solvent on the temperature difference at the boundaries of the container. A series of calculations of the motion of particles in a nonstationary fluid is made.

Keywords: sedimentation, mathematical model, particle deposition in liquid, molecular mass measurement, nanoparticle measurement, concentration measurement, Rayleigh scattering, numerical integration.

Введение

Настоящая работа является продолжением работы [1], которая посвящена построению математической модели измерения концентрации полимерной оболочки на поверхности дисперсных частиц наполнителя, процессе их седиментации. Предложенная нами ранее математическая модель учитывает влияние силы тяжести, Архимедовой силы, силы сопротивления движению. В модели учтено влияние броуновского (теплового) движения жидкости, влияние движения жидкости под действием градиента температуры. Предложена оценка концентрации частиц на основе моделирования рассеяния Рэлея. Управление механическими свойствами дисперсно-армированных полимерных композитов основано на формировании полимерной оболочки на поверхности дисперсных частиц их наполнителя [2], [3]. При построении математических моделей оценки механических свойств композитов обязательным образом учитываются механические свойства полимерных дисперсных частиц [4]. Вместе с тем, определение количественных и численных значений механических свойств полимерных оболочек остается открытым. Напрямую измерить модуль Юнга, коэффициент Пуассона и ряд других параметров полимерных частиц практически невозможно. Однако определить механические характеристики полимерных частиц можно на основе оценки их молекулярной массы [5].

Ранее была предложена математическая модель динамического измерения концентрации двух типов взвешенных в жидкости частиц в процессе их осаждения, основанная на управлении рассеянием света при прохождении лазерного излучения через раствор с взвешенными частицами.

Расчет движения частиц в стационарной жидкости

Рассмотрим уравнение движения частицы [1] и оценим порядки величин, входящих в уравнение, чтобы выбрать величину характерных размерных параметров задачи:

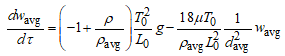    (1)

где w_avg – безразмерная средняя скорость движения частицы, ρ – безразмерная плотность жидкости, ρ_avg – безразмерная средняя плотность частиц, μ – динамическая вязкость, d_avg – безразмерный средний диаметр частиц, T₀ и L₀ – характерное время и расстояние.

Используя эти данные, определим величину размерных параметров задачи, так, чтобы коэффициенты уравнения были порядка единицы, чтобы обеспечить отсутствие ошибок переполнения или потери порядка при решении уравнения. Получим систему уравнений относительно размерных параметров задачи:

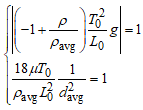      (2) Систему уравнений (2) решим аналитически, получим: 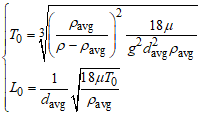       (3) Характерная размерная масса задачи вычисляется, по известным значениям средней плотности, среднего диаметра:       (4)

Выбранные по соотношениям (3) и (4) характерные размерные параметры задачи обеспечивают возможность численного интегрирования уравнений движения частиц без потери порядка и ошибок переполнения. Например, для растворителя со средней плотностью ρ ~ 902 кг/м³ и коэффициентом динамической вязкости μ = 0.40´10^–3 Па×с, при средней плотности частиц ρ_avg = 3000 кг/м³_, их среднего диаметра d_avg = 0.1´10^–6 м, получаем следующие значения для характерных размерных параметров задачи: T₀ = 172.23 с, L₀ = 2.03´10⁵ м и M₀ = 4.72´10^–19 кг.

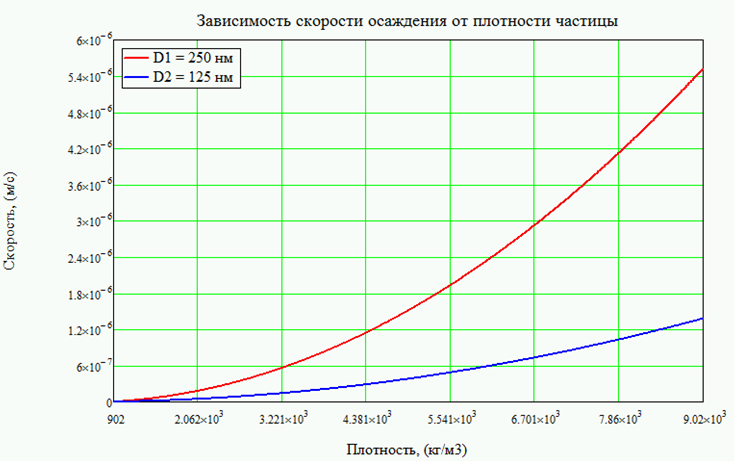
Был проведен численный эксперимент для осаждения двух типов частиц, а именно оксида алюминия (Al₂O₃ – наполнитель) и частиц полимера в этилацетате. Плотность этилацетата ρ = 902 кг/м³, коэффициент динамической вязкости μ = 0.40016´10^–3 Па×с. Средняя плотность частиц первого типа (Al₂O₃) ρ_T1 = 7987 кг/м³. Плотность частиц второго типа (полимер) ρ_T1 = 3000 кг/м³. Средний размер частиц наполнителя d_T1 = 0.25´10^–6 м, и полимера d_T2 = 0.125´10^–6 м. Число частиц наполнителя выбрано равным 1000, и полимера 10000. Предполагалось, что в процессе осаждения частиц на частицы действуют сила тяжести, гидростатическая выталкивающая сила Архимеда и сила сопротивления движению в вязкой жидкости, которая была аппроксимирована для малых чисел Рейнольдса. На рисунке 1 приведены результаты оценки максимальной скорости осаждения частиц в этилацетате в зависимости от плотности и размеров частиц в стационарной жидкости.

Рис. 1 – Зависимость скорости осаждения частиц от их плотности и размеров:

красная линия – осаждение частиц при диаметре 250 нм; синяя линия – при диаметре 125 нм

 

Красной линией на рисунке 1 показана зависимость скорости осаждения частиц с диаметром равным 250 нм, а синей линей для частиц с диаметром 125 нм. Очевидно, что если плотность частицы совпадает с плотностью жидкости, скорость осаждения будет равна нулю, а с увеличением плотности частиц будет увеличиваться их масса, что, соответственно, ведет к росту скорости осаждения. Ограничение максимальной скорости осаждения вызывается силой сопротивления движению жидкости, которая зависит от квадрата диаметра, а масса частицы зависит от куба диаметра, что означает, что более крупные частицы будут оседать с большей скоростью, чем более мелкие.

Определение скоростей и перемещений ансамбля частиц в жидкости можно вести как методом численного интегрирования системы уравнений движения частиц, так и на основе аналитического решения. В ходе численных экспериментов было получено, что относительная погрешность, полученная численно и аналитически, не превышает 10^–8. Что позволяет выбрать любой из методов расчета.

В расчете учитывалось нормальное распределение размеров и плотностей частиц. Для частиц первого типа (Al₂O₃) дисперсия распределения размеров была выбрана равной 1.5×10^–2, дисперсия распределения плотности 4.0×10^–2, для частиц наполнителя дисперсия распределения размеров была выбрана равной 3.0×10^–2, а дисперсия распределения плотности 2.0×10^–2. Температура границ кюветы считалась постоянной и равной 300 К. Диаметр окна контроля концентрации частиц 0.01 м, окно контроля располагалось в середине кюветы по горизонтали и на высоте 0.035 м от нижней границы. Был произведен учет влияния броуновского движения молекул жидкости на скорость и перемещение осаждаемых частиц на основе модели упругого столкновения. Скорость броуновского движения молекул жидкости рассчитывалась по формулам, приведенным в [1], при этом молярная масса этилацетата принималась равной 18.0×10^–3 кг/моль. Учитывалась только модель неупругих столкновений частиц друг с другом, при котором частицы полностью слипаются, образуя новую частицу, с новой массой и скоростью.

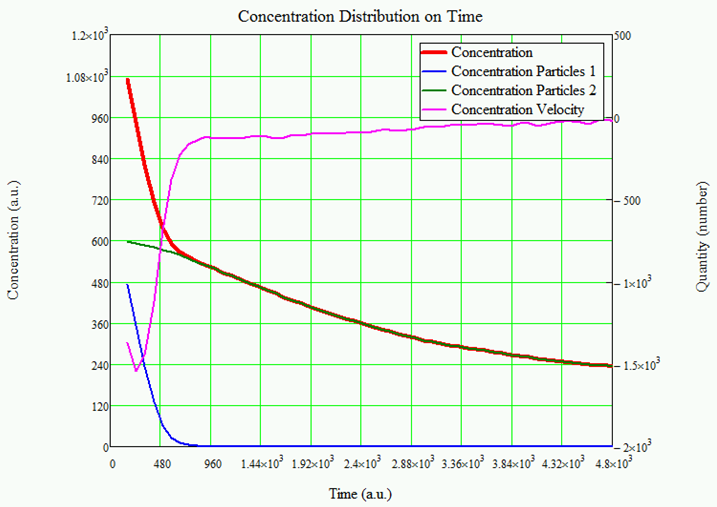
Рассеяние Рэлея, возникающее при прохождении луча лазерного излучения через кварцевую кювету, содержащую раствор с осаждаемыми частицами, моделировалось согласно соотношениям, приведенным в [1], полный свет, загораживаемый частицами в области лазерного луча, приведен на рисунке 2.

Рис. 2 – Результаты математического моделирования изменения концентрации частиц:

красная линия – общая концентрация; синяя линия – концентрация наполнителя; зеленая линия – концентрация полимера; фиолетовая линия – скорость изменения концентрации

 

Как видно из изменения концентрации, показанной на рисунке 2, осаждение тяжелых частиц происходит вначале процесса и очень быстро по времени, после чего происходит осаждение легких частиц.

Расчет полей скоростей и температуры в жидкости

Задача заключается в том, чтобы определить поле температуры и поле скоростей движения жидкости для различных способов нагрева кюветы. Рассмотрим отдельные случаи нагрева кюветы, когда осуществляется нагрев снизу, сверху и варианты симметричного или асимметричного нагрева по бокам кюветы. Отдельно рассмотрим случаи нагрева всей границы или ее части с различными значениями внешней температуры. Результатом исследования должен стать вывод о выборе метода нагрева, который обеспечивает равномерное перемешивание жидкости в кювете с минимальными скоростями, которые обеспечивают левитацию частиц полимера при условии, что частицы наполнителя осядут.

Для всех вариантов численных расчетов движения жидкости расчетная область предполагалась прямоугольной, разбивалась на 51´51 узлов расчетной сетки. В качестве растворителя был взят этилацетат, плотность которого равна 902 кг/м³, динамическая вязкость равна 0.40016×10^–3 Па×с, коэффициент объемного расширения χ₀ = 0.15×10^–3, а коэффициент температурной проводимости α₀ = 0.143×10^–3 м/с². Частицами являлись смесь наполнителя (оксида алюминия) и полимера. Плотность частиц наполнителя составляет 7987 кг/м³, плотность частиц полимера ~3000 кг/м³, размеры частиц алюминия порядка 0.25×10^–6 м, а частиц полимера ~0.125×10^–6 м. Составляющие компонент вектора ускорения свободного падения g_x = 0, g_z = –1 м/с².

Поля функций тока, температуры и вихря на каждой итерации вычислялись с относительной погрешностью, не превышающей 10^–5, а итерационный алгоритм сходимости полного решения системы уравнений велся с относительной погрешностью, не превышающей 10^–4. При этом максимальное количество итераций при решении уравнения вихря не превышало 12, а для решения уравнений температуры и функций тока на каждом итерационном шаге интегрирования всей системы уравнений в целом выполнялось не более двух итераций. Значения полей температуры и скоростей на всех графиках в данном разделе приведены в размерных величинах задачи.

Численный расчет полей скоростей и температуры производится для кюветы геометрические размеры сечения которой в плоскости перпендикулярной оси лазерного излучения составляют 0,05х0,05 м. Минимальное значение характерной температуры (K_Min) было выбрано равным 300 К, поскольку нагрев осуществляется в лабораторной установке, которая размещена в помещении с комнатной температурой. В качестве максимального значения характерной температуры (K_Max) может быть выбрано произвольное значение, большее минимального значения. Вместе с тем, чтобы обеспечить безразмерное значение температуры в пределах от нуля до единицы, для каждого конкретного варианта расчета в качестве максимальной температуры выбиралось то значение температуры, которое задавалось на границе области. Учитывая то, что в качестве растворителя использовалась весьма летучая и быстро испаряющаяся жидкость (этилацетат), максимальные значения температуры в расчетах не задавались превышающими 325 К.

Стационарное уравнение движения жидкости имеет вид [1]:

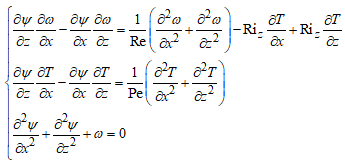     (5)

где в качестве коэффициентов использованы число Рейнольдса (Re), число Ричардсона (Ri) и число Пекле (Pe), для которых использованы известные обозначения:

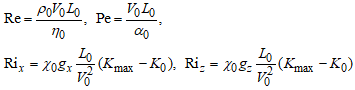      (6)

Система уравнений, записанная в терминах чисел Рейнольдса, Ричардсона и Пекле, позволяет выбрать произвольный набор характерных размерных параметров задачи, а именно – характерную длину, минимальную и максимальную температуры и характерную скорость задачи. Использование чисел Рейнольдса, Ричардсона и Пекле, позволяет сформулировать дополнительное условие на выбор характерных величин, которое заключается в том, что мы можем потребовать равенство единице числа Ричардсона в первом уравнении, записав условие в виде:

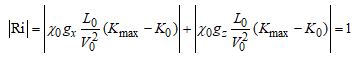       (7)

Имея характерную длину и температуры, а также значения коэффициента объемного расширения и ускорения свободного падения, можно получить значение характерной скорости задачи из соотношения (7):

      (8)

и вычислить значения для чисел Рейнольдса, Ричардсона и Пекле.

Задав в качестве характерной длины задачи геометрический размер кюветы (0,05 м), подставив значения характерных температур, и параметры растворителя, получаем величину характерной скорости V₀ ≈ 0.019 м/с, числа Рейнольдса Re ≈ 955, Пекле Pe ≈ 6703 и Ричардсона Ri_z = –1. Знак числа Ричардсона обусловлен знаком g_z. При этом безразмерное расстояние и температура изменяются от 0 до 1. Знак приблизительного равенства для характерной скорости, и чисел Рейнольдса и Пекле приведен для того, чтобы указать порядок их величин. Их численные значения зависят от заданных характерных (минимальной и максимальной) температур и для каждого варианта расчета несколько отличаются. Указанное число Рейнольдса Re ≈ 1000, определяет, что течение в области является ламинарным.

Нагрев нижней границы кюветы

При нагреве кюветы снизу предполагается, что нижняя граница (или ее часть) нагревается до постоянной температуры, которая не меняется со временем. На левой и правой границе кюветы температура считается равной температуре окружающей среды. Расчет производился для нагрева всей нижней поверхности и 3/5 ее центральной части. В работе приведены расчеты для двух вариантов нагрева до 305 и 315 К.

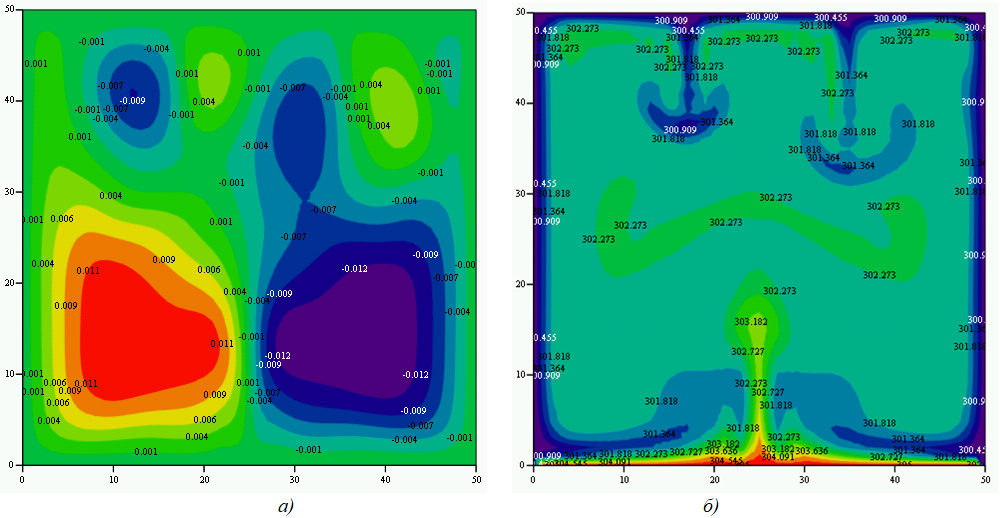
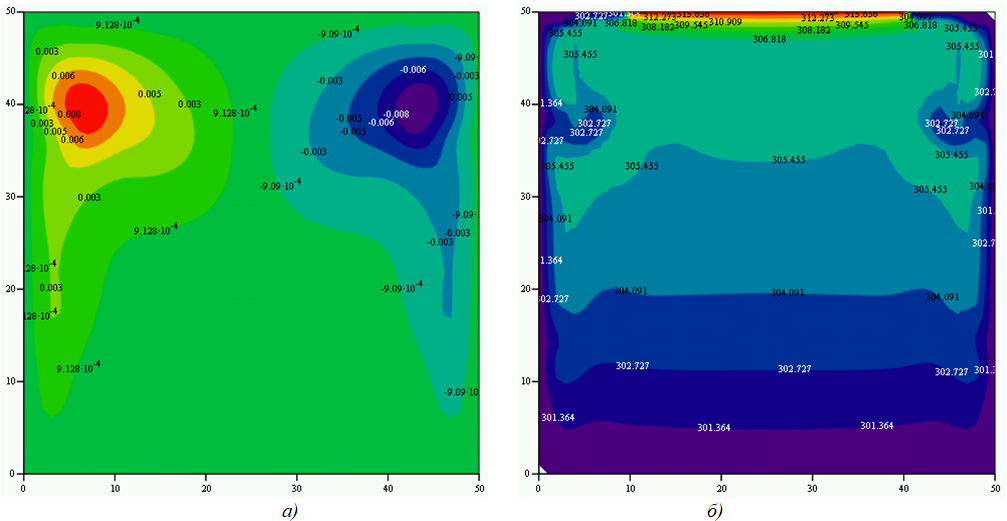
На рисунке 3 приведены результаты расчетов полей функции тока, температуры и скоростей для варианта нагрева и поддержания температуры нижней границы в 305 К, температура на боковых и верхней границах – 300 К. Поле вихря на рисунках для всех вариантов расчетов не приводится поскольку оно не несет в себе информации о физике явления. Расчеты показали, что максимальное вертикальной и горизонтальной составляющей скорости составило ~0,003 м/с и ~0,002 м/с, соответственно.

 

Рис. 3.1 – Нагрев нижней границы 305 К, на боковых и верхних границах температура 300 К:

а) функции тока; б) температура

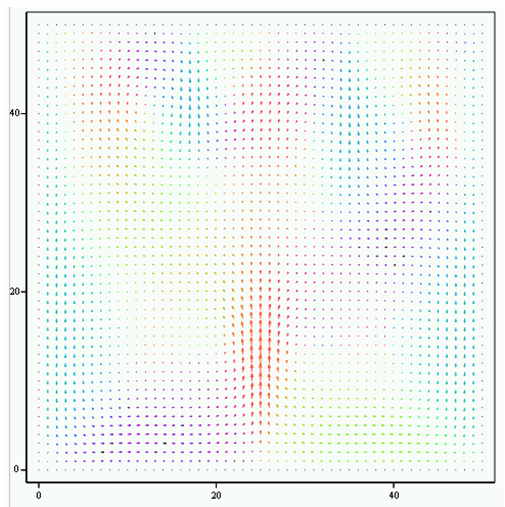
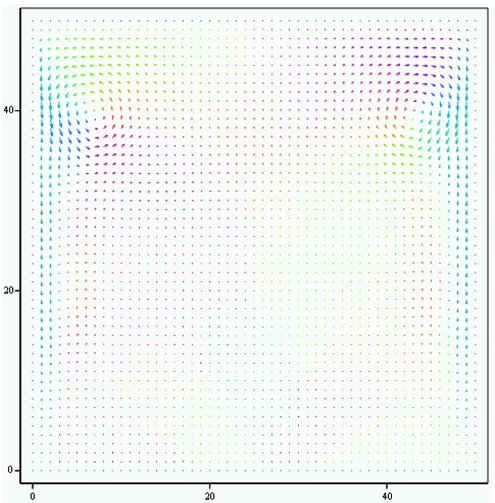
Рис. 3.2 – Нагрев нижней границы 305 К, на боковых и верхних границах температура 300 К – скорости

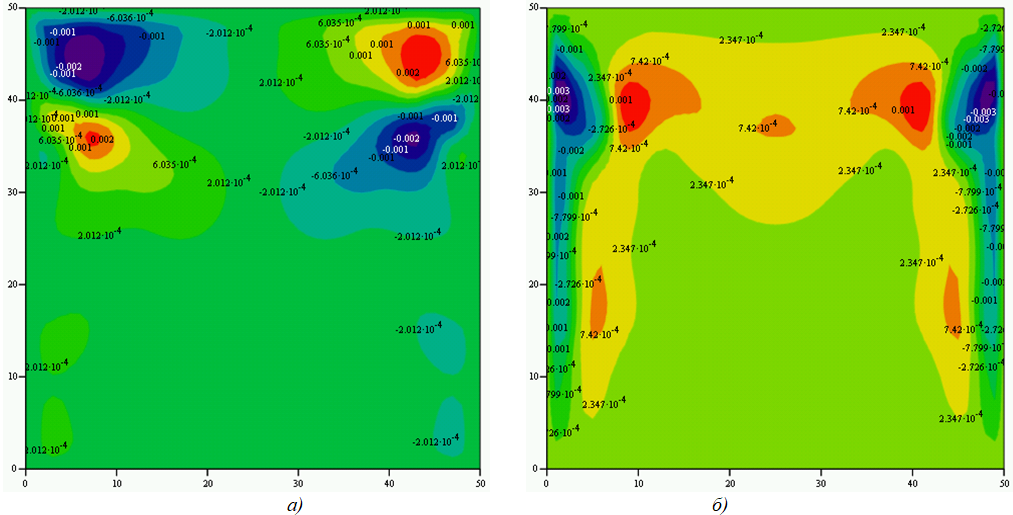
Рис. 3.3 – Нагрев нижней границы 305 К, на боковых и верхних границах температура 300 К:

а) горизонтальные скорости; б) вертикальные скорости

 

На рисунке 3.1а видно, что в кювете образовалось симметричное относительно центральной вертикальной оси течение, которое формирует шесть ячеек Бенара, представляющие собой упорядоченное движение в виде конвективных ячеек в форме цилиндрических валов (или правильных шестигранных структур) в слое вязкой жидкости с вертикальным градиентом температуры. Структура формирования ячеек Бенара, связанная с группировкой их по три разно направленных вращающихся структур связана с тем, что кювета по бокам ограничена, а на боковых поверхностях поддерживается такая же температура, как на верхней границе. Энергия нагрева не достаточна для того, чтобы восходящий поток жидкости посредине кюветы доходил до самого верха. Максимальная скорость восходящего потока жидкости возникает в середине кюветы, в ее нижней трети части по высоте и составляет порядка 0,003 м/с.

Увеличение температуры нижней границы до 315 К приводит к том, что подводимой внешней энергии уже достаточно для того, чтобы образовались две симметричные ярко выраженные ячейки Бенара. Максимальное значение вертикальной составляющей скорости в этом случае увеличивается до 0,005 м/с. Движение жидкости в случае более интенсивного нагрева нижней границы становится более упорядоченным, а поле температуры более равномерным.

Интересен результат расчета для случая, когда не вся нижняя граница поддерживается при фиксированной температуре, а лишь ее часть, поскольку именно такой вариант проще всего и целесообразнее реализовать на практике. Сохранив значение поддерживаемой температуры в 315 К, осуществим нагрев на срединном участке нижней границы, который составляет 3/5 от ширины кюветы. То есть на боковой и верхней границе кюветы, на левой и правой частях нижней границы (1/5 от ширины) поддерживается температура в 300 К, а середина нижней границы нагревается и поддерживается при температуре 315 К. Картина движения жидкости и в этом случае более или менее сохраняет симметрию относительно вертикальной оси. Максимальное значение скоростей и в этом случае не превышает 0,005 м/с, с равномерным нагревом всей жидкости.

В связи с тем, что восходящий поток в центре области не обеспечивает равномерного распределения скоростей вдоль вертикальной оси, и максимальные значения скоростей находятся в нижней части кюветы, можно сделать вывод о том, что равномерный нагрев всей нижней границы предпочтительнее для обеспечения равномерного поля температуры и вертикальных составляющих скоростей в жидкости.

Нагрев верхней границы кюветы

В ряде случаев для натурного эксперимента предпочтительнее осуществлять нагрев кюветы со стороны верхней границы. Это может быть обусловлено как конструкций самой кюветы, так и конструктивной особенностью нагревательного элемента. В связи с этим имеет смысл рассмотреть отдельно такие случаи тоже.

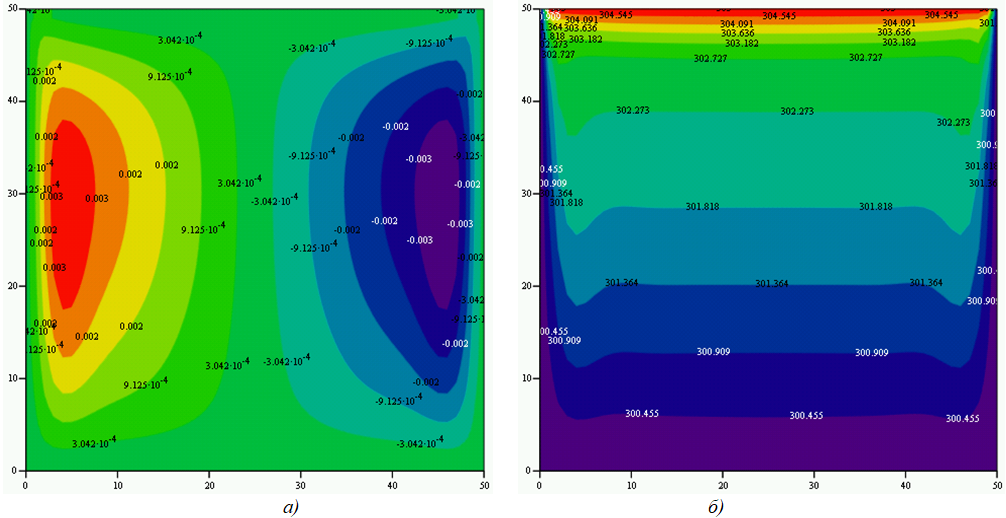
На рисунке 4 приведены результаты расчетов для случая, когда верхняя граница кюветы держится при постоянной температуре 305 К.

Рис. 4.1 – Нагрев верхней границы до 305 К, на боковых и верхних границах температура 300 К:

а) функции тока; б) температура

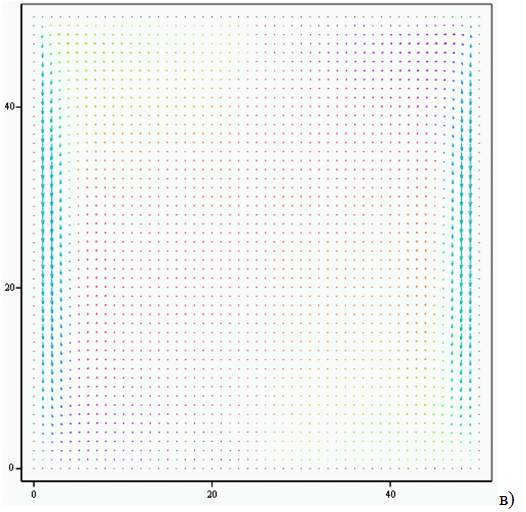
Рис. 4.2 – Нагрев верхней границы до 305 К, на боковых и верхних границах температура 300 К – скорости

Рис. 4.3 – Нагрев верхней границы до 305 К, на боковых и верхних границах температура 300 К:

а) горизонтальные скорости; б) вертикальные скорости

 

Как можно видеть, в этом случае образуются две ярко выраженных ячейки Бенара, а поле температур образует слоистую структуру с практически вертикальным градиентом. Интенсивность движения жидкости в этом случае существенно ниже, чем в случае нагрева нижней границы кюветы. Максимальные значения скоростей, наблюдаются лишь в нисходящих потоках вблизи боковых границ. Практически весь объем жидкости движется в равномерном восходящем потоке, причем, восходящая скорость такого потока практически одинакова для всего объема жидкости. Нисходящие потоки интенсивнее, но они протекают лишь вблизи левой и правой границ области. Для пояснения этого факта на рисунках 4.3а и 4.3б приведены горизонтальные и вертикальные составляющие скоростей в жидкости. Как можно видеть, практические во всем объеме наблюдается восходящее течение жидкости с одинаковой для всего объема скоростью восходящего движения. Вертикальная скорость восходящего потока не превышает 0,0001 м/с. Одновременно с этим, восходящий поток более равномерен для всей области кюветы, что снижает требования к точному позиционированию лазерного излучения, с помощью которого осуществляется контроль концентрации частиц.

Дальнейшее увеличение температуры нагрева внешней границы не меняет общей структуры течения в кювете и не приводит к существенному изменению ни характера течения, ни его кинематических параметров. К примеру, увеличение температуры верхней границы до 325 К приводит лишь к двукратному увеличению скорости восходящего потока, при сохранении общей структуры течения. В исследованиях показано, что увеличение температуры верхней границы в указанном диапазоне изменяет лишь количественные характеристики движения жидкости, не меняя его структуру в целом.

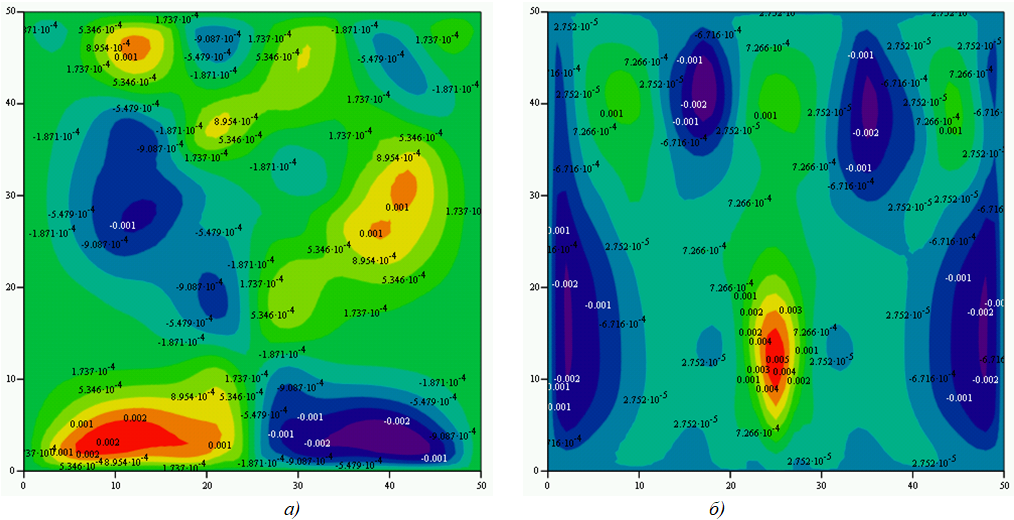
Нагрев средней 3/5 части верхней границы до 305 К также не приводит к изменению общей структуры течения. Увеличение температуры нагреваемой 3/5 части верхней границы ведет к образованию завихрений вблизи верхнего правого и левого углов области (Рисунок 5) с одновременным смещением области интенсивного восходящего потока к верхней части середины области. Этот факт служит рекомендациям по установке области контроля концентрации частиц. Дальнейшее увеличение температуры до 315 К приводит более равномерному перемешиванию жидкости, с образованием заметной области с равномерной температурой в центре. Максимальная скорость восходящего потока возрастает до 0,001 м/с. Однако в области кюветы образуется значительное количество вихрей, с формированием сложной структуры течения.

Рис. 5.1 – Нагрев 3/5 средней части верхней границы до 315 КЖ на боковых и верхних границах температура 300 К:

а) функции тока; б) температура

Рис. 5.2 – Нагрев 3/5 средней части верхней границы до 315 КЖ на боковых и верхних границах температура 300 К – скорости

Рис. 5.3 – Нагрев 3/5 средней части верхней границы до 315 КЖ на боковых и верхних границах температура 300 К:

а) горизонтальные скорости; б) вертикальные скорости

 

Нагрев жидкости со стороны верхней границы при малых температурах обеспечивает более равномерное распределение поля скоростей в случае, если верхняя граница нагревается полностью. Однако это не приводит к заметному перемешиванию жидкости в силу того, что скорости течения малы. Симметричный нагрев части верхней границы ведет к тому, что структура течения жидкости становится более сложной, образуются встречные и направленные в разные стороны вихри.

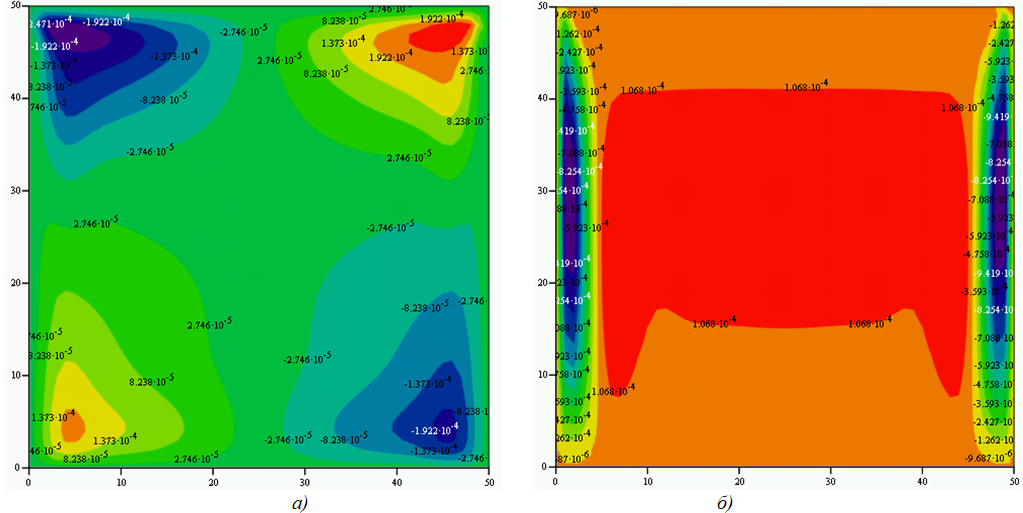
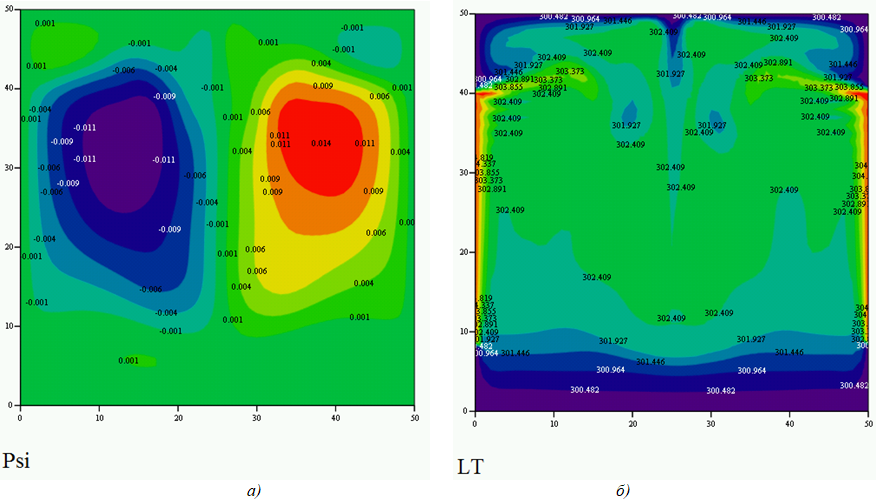
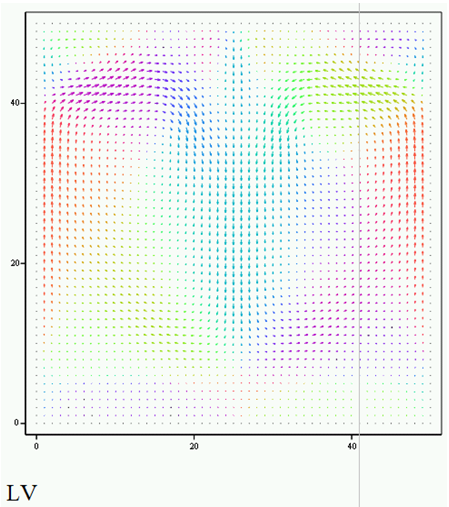
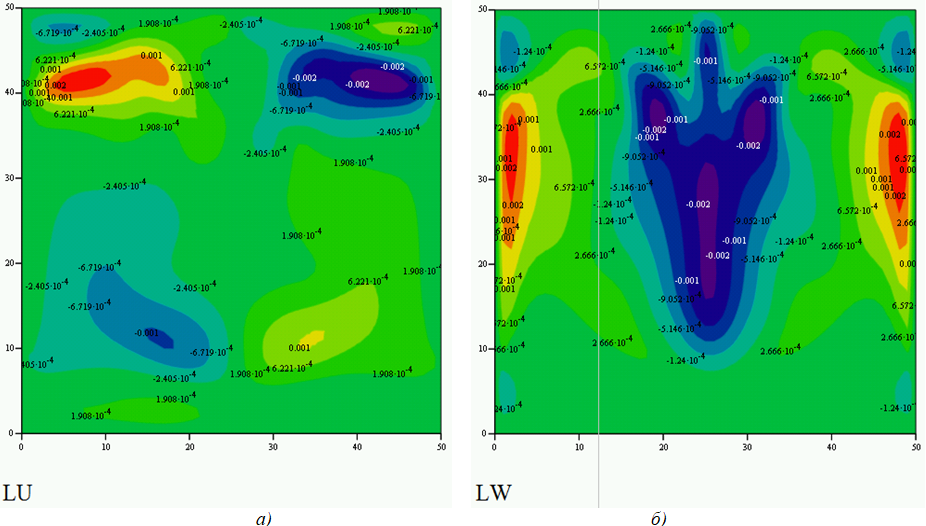
Нагрев боговых границ кюветы

Результаты расчета для симметричного нагрева боковых частей участков границы до 305 К приведены на рисунке 6. Нагрев боковых поверхностей приводит к тому, что восходящий поток формируется вблизи левой и правой границ области, а в середине области возникает нисходящее движение жидкости.

 

Рис. 6.1 – Нагрев 3/5 частей боковых границ температуры до 305 К:

а) функции тока; б) температура

Рис. 6.2 – Нагрев 3/5 частей боковых границ температуры до 305 К – скорости

Рис. 6.3 – Нагрев 3/5 частей боковых границ температуры до 305 К:

а) горизонтальные скорости; б) вертикальные скорости

Нагрев кюветы с боковых границ обеспечивает большую скорость движения жидкости, и вследствие этого, большую степень прогрева внутренней части жидкости. Скорости при боковом симметричном нагреве до 305 К обеспечивает скорости движения жидкости в два раза большие, чем нагрев области с нижней стороны границы – до 0,002 м/с. Увеличение температуры на боковых границах до 315 К увеличивает скорости движения до 0,007 м/с, при этом внутренняя часть жидкости прогревается до температуры 307 К. Обеспечить одновременный нагрев левой и правой границ области с одинаковой температурой достаточно сложно. Ввиду этого были сделаны варианты расчетов, предусматривающие варианты асимметричного нагрева левой и правой границы. Асимметрия температуры на границе области даже при небольшой разнице температур меняет структуру движения жидкости.

Численное решение системы уравнений, записанной в условиях приближения Буссинеска, когда учет зависимости плотности от температуры производится только в массовых силах, было получено в условиях полностью непроницаемых границ и для случая установившегося течения. Анализ результатов расчетов показал, что характер жидкости в емкости достаточно сильно зависит от условий симметрии температуры на внешней границе. Любая, даже незначительная асимметрия внешнего поля температуры приводит к возникновению асимметричного движения внутри области. Подтверждена априорная оценка зависимости скоростей движения жидкости от величины внешней приложенной температуры. Наиболее эффективным методом нагрева кюветы с жидкостью, содержащей взвесь частиц наполнителя и полимера, с точки зрения равномерности восходящего потока жидкости в области оптического контроля является нагрев ее верхней границы.

Зависимость скоростей движения жидкости в окне контроля от температуры на границе кюветы

Как было показано выше, на скорость осаждения частиц, прежде всего, влияет скорость потока жидкости, которая вовлекает частицы в свое движение. Во вторую очередь на движение частицы влияет температура жидкости, которая оказывает вклад на броуновское движение молекул жидкости, которые в свою очередь воздействуют на осаждаемые частицы, вызывая их случайное перемещение. Исследование результатов расчетов, выполненных для различных вариантов нагрева внешних границ кюветы, показало, что наиболее эффективным является нагрев верхней границы кюветы при одинаковой температуре на других границах. Эффективность метода нагрева определялась равномерностью восходящего потока жидкости в области оптического контроля концентрации частиц.

В силу вышесказанного, была поставлена задача определения зависимости скорости восходящего потока в зоне окна контроля концентрации от температуры верхней границы жидкости. Построение такой зависимости велось путем численного решения уравнений движения жидкости при разных значениях температуры верхней границы. Боковые и нижняя границы кюветы поддерживались при комнатной температуре (300 К), а температура верхней границы варьировалась в диапазоне от 301 до 325 К с дискретным шагом 1 К. Диаметр окна контроля был выбран равным 0.01 м, окно контроля располагалось по середине кюветы (x_c = 0.025м) по горизонтали и на высоте (z_c = 0.035м) от низа кюветы по вертикали. Течение в кювете при таком способе нагрева симметричное, и в качестве вертикальной составляющей скорости принималось среднее значение скорости в окне контроля, а для горизонтальных составляющих скоростей приведен модуль максимального значения скорости, в окне контроля, поскольку среднее значение горизонтальной составляющей скорости равно нулю.

Зона оптического контроля концентрации частиц была выбрана так, чтобы в области контроля было равномерное ламинарное течение жидкости, без образования вихрей (встречных и разнонаправленных течений жидкости). Дополнительным пожеланием к выбору области контроля концентрации служило требование равномерности поля температуры в этой области жидкости.

Данные о температуре верхней границы, горизонтальной и вертикальной составляющей скорости в жидкости и температуре жидкости в окне контроля сведены в таблице 1. В таблицу 1 дополнительно добавлены результаты расчетов, выполненных для температуры верхней границы, нагретой до 300.001, 300.010, 300.1 и 300.2 К.

Таблица 1 – Данные численного расчета скоростей и температуры в окне контроля концентрации в зависимости от температуры верхней границы

№	Температура на верхней границе	Температура в окне контроля	Горизонтальные составляющие скорости	Вертикальные составляющие скорости
	К	К	м/с	м/с
1	300.001	300.000	1.200×10–6	2.781×10–6
2	300.01	300.003	5.404×10–6	1.268×10–5
3	300.1	300.024	9.141×10–6	2.551×10–5
4	300.2	300.050	1.045×10–5	3.217×10–5
5	301	300.314	1.818×10–5	6.375×10–5
6	302	300.701	2.392×10–5	8.674×10–5
7	303	301.117	2.855×10–5	1.037×10–4
8	304	301.549	3.248×10–5	1.182×10–4
9	305	301.993	3.574×10–5	1.306×10–4
10	306	302.445	3.826×10–5	1.412×10–4
11	307	302.903	4.079×10–5	1.509×10–4
12	308	303.367	4.268×10–5	1.594×10–4
13	309	303.843	4.498×10–5	1.682×10–4
14	310	304.305	4.678×10–5	1.757×10–4
15	311	304.779	4.866×10–5	1.829×10–4
16	312	305.255	5.054×10–5	1.901×10–4
17	313	305.734	5.258×10–5	1.970×10–4
18	314	306.214	5.433×10–5	2.033×10–4
19	315	306.697	5.593×10–5	2.094×10–4
20	316	307.180	5.804×10–5	2.158×10–4
21	317	307.666	5.988×10–5	2.214×10–4
22	318	308.152	6.162×10–5	2.265×10–4
23	319	308.639	6.339×10–5	2.315×10–4
24	320	309.128	6.506×10–5	2.368×10–4
25	321	309.617	6.658×10–5	2.419×10–4
26	322	310.107	6.805×10–5	2.469×10–4
27	323	310.598	6.957×10–5	2.519×10–4
28	324	311.089	7.109×10–3	2.565×10–4
29	325	311.581	7.265×10–3	2.612×10–4

 

На основании данных, полученных в результате расчетов, можно построить зависимость температуры и скорости восходящего потока в жидкости от температуры нагрева верхней границы области. Если на протяжении определенного интервала времени концентрация частиц в окне контроля не будет меняться, это будет свидетельствовать о том, что скорость осаждения частиц совпала по модулю (и противоположна по знаку) со скоростью восходящего потока. В свою очередь, скорость осаждения частиц в жидкости напрямую зависит от плотности (или массы) частиц. Что позволяет связать плотность частиц с температурой нагрева верхней границы. Приравняв скорость восходящего потока жидкости к скорости осаждения частиц, можно вычислить плотность не осаждаемых частиц.

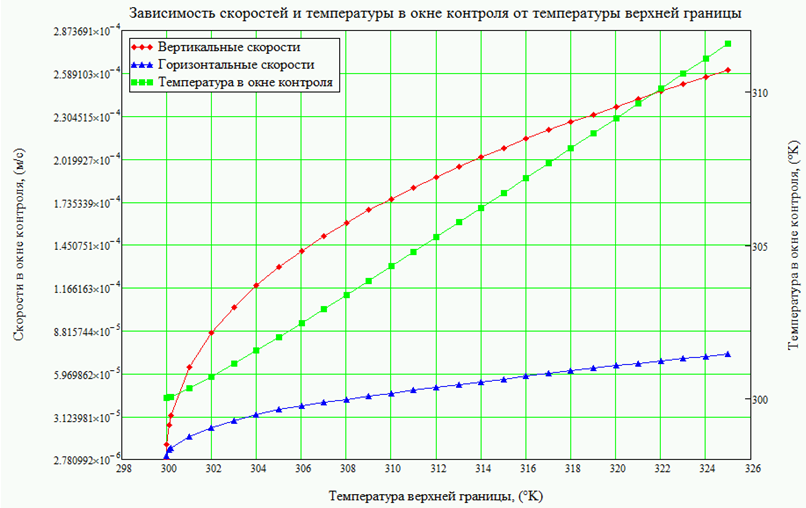
Рис. 7– Зависимость горизонтальной и вертикальной составляющей скоростей и температуры жидкости в окне контроля концентрации в зависимости от температуры верхней границы

 

Графики, приведенные на рисунке 7, позволяют сделать наблюдение о том, что температура в окне контроля концентрации растет практически линейно с ростом температуры верхней границы. Зависимость же скоростей как горизонтальной, так и вертикальной, имеет логарифмический характер.

На основе численного решения системы уравнений, описывающих движение жидкости, и сравнения максимальных скоростей осаждения частиц, можно сформулировать требования к методу измерений концентрации и массы частиц. Подобные характерные зависимости могут быть получены для любой жидкости, в которой проводится анализ осаждения частиц.

Расчет движения частиц в нестационарной жидкости

Первоначально решается система уравнений движения жидкости с соответствующими вариантами граничных условий для жидкости независимо от движений частиц. Для чего система уравнений движения жидкости переводится в безразмерную форму, с применением характерных для жидкости размерных параметров задачи. После окончательного расчета полей функций тока, вихря и температуры, осуществляется расчет полей скоростей по формулам. Полное решение системы уравнений движения жидкости (поля скоростей и температуры) переводится в размерные величины и передается в программу расчета движения частиц и определения их концентрации в окне контроля.

Графическая визуализация одновременного движения всех частиц в жидкости представляет собой некоторую сложность, поэтому графическое представление траекторий движения приведены для пары частиц – одной «тяжелой» частицы (наполнителя) и одной «легкой» частицы (полимера). Для расчета движения частиц, контрольные частицы наполнителя и полимера были размещены в середину области по вертикали и смещены на 5% влево и вправо относительно вертикальной оси симметрии. Начальные значения скоростей частиц равны нулю. Плотность частиц наполнителя примерно в четыре раза больше, чем плотность жидкости, а плотность частиц полимера была выбрана лишь на 10 процентов больше, чем плотность жидкости.

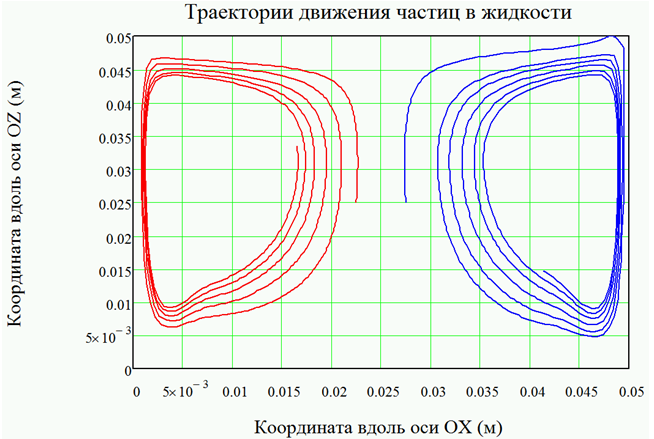
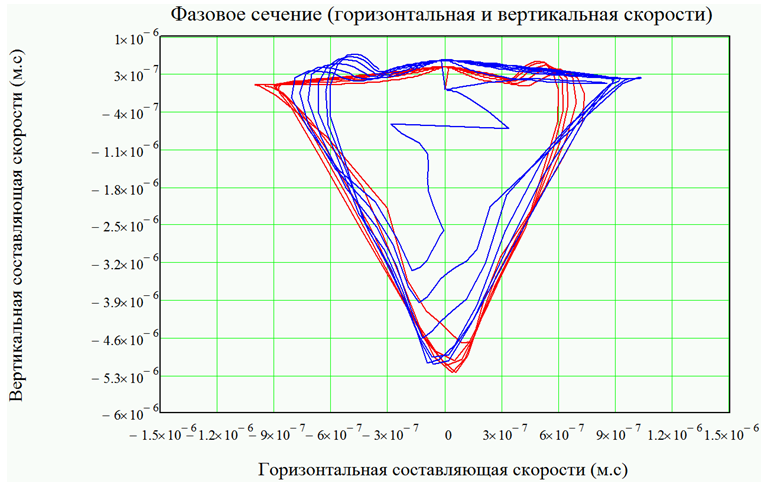
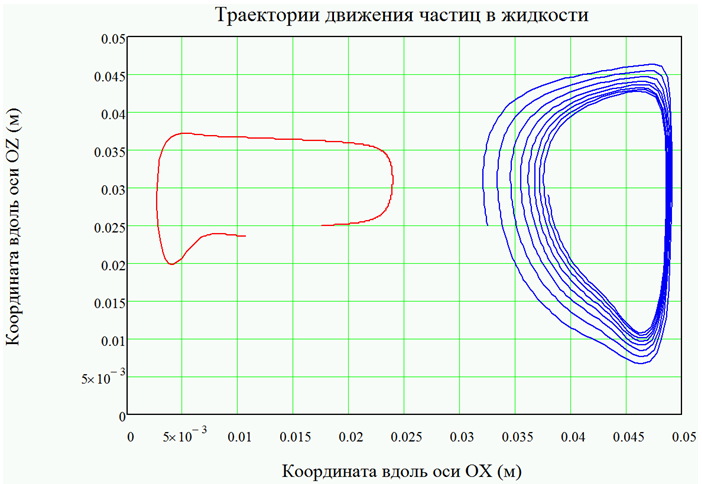
На рисунке 8.1 приведен пример расчета траекторий движения частиц в этилацетате (ρ₁ = 902 кг/м³), когда верхняя граница кюветы поддерживается при постоянной температуре 301 К, а нижняя и боковые границы поддерживаются при температуре 300 К. Красной линией на рисунке 8.1 приведена траектория частицы наполнителя (ρ₁ = 8000 кг/м³), синей линией – траектория частицы полимера (ρ₂ = 2000 кг/м³). На рисунке 8.2 приведено сечение в фазовой плоскости (горизонтальная и вертикальная составляющие скорости). Можно видеть, что движение жидкости оказывает существенное влияние на движение частиц, вовлекая их в собственное движение. При отсутствии массы и сил сопротивления частицы перемещались бы в жидкости строго вдоль линий тока, однако наличие сил сопротивления движению и сил тяжести ведет к тому, что траектория движения частиц со временем расходятся с линиями тока. Вместе с этим, видно (рисунок 8.2), что частица практически мгновенно принимает скорость движения, крайне близкую к локальной скорости движения жидкости.

Рис. 8.1 – Движение частиц в жидкости, нагретой со стороны верхней границы до 301 К, на нижней и боковых границах поддерживается температура 300 К – траектории

Рис. 8.2 – Движение частиц в жидкости, нагретой со стороны верхней границы до 301 К, на нижней и боковых границах поддерживается температура 300 К – фазовое сечение

 

Для выбранного начального положения частиц и движения жидкости, заметим, что частицы могут соударяться с границами области. На рисунке 8.1 можно наблюдать отскок частицы полимера (синяя линия) от верхней и от правой границ области. В момент соударения с границей области (соударение частиц о границы области считались абсолютно упругим) соответствующая границе нормальная составляющая скорости меняет знак.

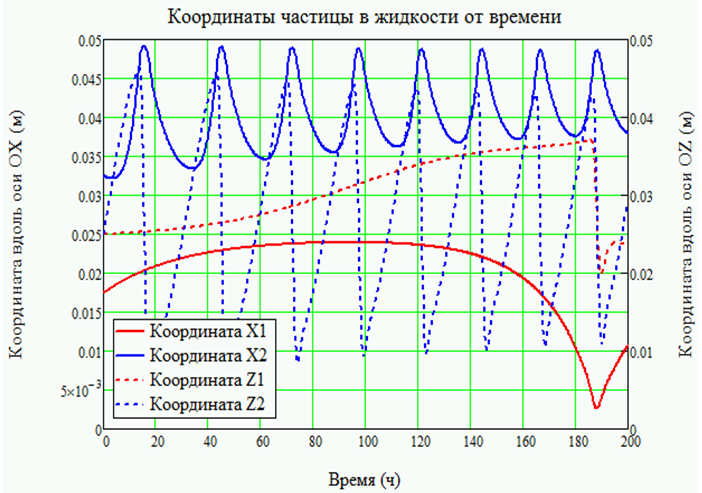
На рисунке 9.1 приведены траектории движения сверхтяжелой частицы, плотность которой ρ₁ = 14125 кг/м³ почти в два раза больше плотности оксида алюминия (красная линия), и легкой частицы (ρ₂ = 2000 кг/м³) в жидкости (ρ = 902 кг/м³). На рисунке 9.2 приведены зависимости координат сверхтяжелой частицы от времени. Из зависимостей, приведенных на рисунках 9 можно сделать вывод о том, что тяжелая частица с трудом увлекается движением жидкости.

Рис. 9.1 – Движение сверхтяжелой и легкой частиц в жидкости, нагретой со стороны верхней границы до 301 К, на нижней и боковых границах поддерживается температура 300 К – траектории

Рис. 9.2 – Движение сверхтяжелой и легкой частиц в жидкости, нагретой со стороны верхней границы до 301 К, на нижней и боковых границах поддерживается температура 300 К – координаты в зависимости от времени

 

Сверхтяжелая частица, начиная свое движение в точке с координатами (0.0025, 0.025), тратит почти 180 часов, на вертикальный подъем, и потом за 20 часов совершает движение вдоль линий тока. Легкая частица за это же время успевает совершить шесть полных оборотов.

Заключение

Проведены оценки величин скоростей осаждения частиц в стационарной жидкости в зависимости от их размеров и плотностей на основе аналитического решения уравнения движения частиц. Выполненные оценки позволяют определить как время седиментации, так и сформулировать требования к методу измерения частиц различных размеров и плотности.

Проведена оценка зависимости времени седиментации в растворителе на основе индивидуального решения уравнений движения для каждой частицы. Проведены расчеты, позволяющие количественно оценить концентрацию частиц двух типов (наполнителя и полимера) в окне контроля. Результаты расчетов хорошо согласуются с предсказаниями математической модели и эмпирическими оценками, что служит подтверждением корректности выбора математической модели и численной ее реализации.

Выполнены расчеты полей скоростей и температуры, возникающей в жидкости для различных вариантов нагрева внешних границ кюветы. Вертикальная симметрия формы течений жидкости, возникающей в кювете при симметричном относительно вертикальной оси нагреве, свидетельствует о корректности математической модели и численного решения системы уравнений движения жидкости. Выполненные расчеты движения жидкости, позволили сформулировать условие, при котором температура и скорости в окне контроля концентрации будут максимально равномерными, а течение жидкости будет максимально ламинарным.

Проведены оценки горизонтальной и вертикальной составляющей скоростей и температуры жидкости в окне контроля концентрации в зависимости от температуры верхней границы. Показано, что температура в окне контроля концентрации в зависимости от температуры на верхней границе может быть аппроксимирована линейной зависимостью. В то время как локальные скорости жидкости в окне контроля концентрации растут по логарифмическому закону.

Оценки скоростей и температуры, возникающих в жидкости, позволили сделать предположение о том, что даже незначительный перепад температур на границе области вызовет заметное движение жидкости, которое увлекает за собой движение частиц. Выполненные расчеты для движения частиц в нестационарной жидкости, подтвердили данное предположение.

Финансирование Работа выполнена при поддержке Минобрнауки России (соглашение номер 075-03-2020-051/3 от 09.06.2020, номер темы fzsu-2020-0021) в части постановки физической задачи моделирования, верификации данных и полученных результатов и Министерства науки и высшего образования Российской Федерации (соглашение номер 075-03-2020-051, номер тему fzsu-2020-0020) в части построения математической модели и её реализации.

Funding Danilaev was funded by Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-03-2020-051/3, topic No. fzsu-2020-0021) in part of physical task formulation, data and results verification. A.Zh. Sakhabutdinov was funded by Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-03-2020-051, topic No. fzsu-2020-0020) in part of mathematical model construction, training and tuning, and realization.

Конфликт интересов Не указан

Conflict of Interest None declared

Список литературы / References

1. Хуссейн С.М.Р.Х. Математическая модель измерения концентрации наночастиц в жидкости в процессе их осаждения / С.М.Р.Х. Хуссейн, О.Г. Морозов, М.П. Данилаев и др. // Международный научно-исследовательский журнал. 2020. 12(102). С. 94. DOI: 10.23670/IRJ.2020.102.12.016
2. Ахмадеев А. А. Влияние толщины полимерной оболочки на поверхностях субмикронных частиц наполнителя на свойства полимерной композиции / А. А. Ахмадеев, Е. А. Богослов, М. П. Данилаев и др. // Механика композитных материалов. 2020. Т. 56. № 2. С.357.
3. Шилько С.В. Анализ механических свойств трансверсально-изотропных композитов с учетом межфазного слоя / С.В. Шилько, Ю.М. Плескачевский, С.В. Панин и др. // Вестник национальной академии наук Белоруссии. 2014. №1. С. 12.
4. Астафуров С.В. Исследование влияния свойств межфазных границ на механические характеристики металлокерамических композитов / С.В. Астафуров, Е.В. Шилько, В.Е. Овчаренко и др.// Физическая мезомеханика. 2014. Т.17. № 3. С. 53.
5. Rajib Ghosh Chaudhuri Core/Shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications / Rajib Ghosh Chaudhuri, Santanu Paria // Chem. Rev. 2012. V.112. № 4. P.2373.
6. Сахабутдинов Ж.М. Анализ дискретных моделей движения точки / Ж.М. Сахабутдинов. – Казань: ИММ РАН, 1995–196 с.
7. Кондратенко П.С. Теоретические основы гидродинамики и теплопереноса / П.С. Кондратенко. Москва: Институт проблем безопасного развития атомной энергетики РАН, 2003. 68 с.
8. Гидродинамика: учеб. Пособие для студентов нематематических факультетов / А.Б. Мазо, К.А. Поташев. – Казань: Казан. ун-т, 2013. – 2-е изд. – 128 с
9. Ван-Дайк М. Альбом течений жидкости и газа / М. Ван-Дайк. М.: Мир, 1986 – c. 84, рис. 139–140

Список литературы на английском языке / References in English

1. Hussain S. M. R. H. Matematicheskaja model' izmerenija koncentracii nanochastic v zhidkosti v processe ikh osazhdenija [Mathematical Model for Measuring the Concentration of Nanoparticles in a Liquid During Their Deposition] / S. M. R. H. Hussein, O. G. Morozov, M. P. Danilaev et al. // Mezhdunarodnyjj nauchno-issledovatel'skijj zhurnal [International Research Journal]. 2020. 12(102), p. 94. DOI: 10.23670/IRJ.2020.102.12.016 [in Russian]
2. Akhmadeev A. Vlijanie tolshhiny polimernojj ob-olochki na poverkhnostjakh submikronnykh chastic napolnitelja na svojjstva polimernojj kompozicii [Influ-ence of the Thickness of the Polymer Shell on the Surfaces of Submicron Filler Particles on the Properties of the Polymer Composition] / A. A. Akhmadeev, E. A. Bogoslov, M. P. Danilov // Mekhanika kompozitnykh materialov [Mechanics of Composite Materials]. 2020. Vol. 56. No. 2, p. 357 [in Russian]
3. Shilko S. V. Analiz mekhanicheskikh svojjstv transversal'no-izotropnykh kompozitov s uchetom mezhfaznogo sloja [Analysis of the Mechanical Properties of Transversally Isotropic Composites, Taking Into Account the Interfacial Layer] / S. V. Shilko, Yu. m. Pleskachevsky, S. V. Panin et al. // Vestnik nacional'nojj akademii nauk Belorussii [Proceedings of the Na-tional Academy of Sciences of Belarus]. 2014. №1, p.12 [in Russian]
4. Astafurov S. V. Issledovanie vlijanija svojjstv mezhfaznykh granic na mekhanicheskie kharakteristiki metallokeramicheskikh kompozitov [Investigation of the Influence of the Properties of Interphase Boundaries on the Mechanical Characteristics of Metal and Ce-ramic Composites] / S. V. Astafurov, E. V. Shilk, V. E. Ovcharenko et al. // Fizicheskaja mezomekhanika [Physical mesomechanics journal] 2014. Vol. 17. No. 3, p. 53 [in Russian]
5. Rajib Ghosh Chaudhuri, Santanu Paria Core / Shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications // Chem. Rev. 2012. V.112. № 4. P.2373.
6. Sakhabutdinov Zh. M. Analiz diskretnykh modelejj dvizhenija tochki [Analysis of Discrete Mod-els of the Motion of a Point] / Zh. M. Sakhabutdinov. - Kazan: Institute of Mechanics and Engineering - Sub-division of the Federal State Budgetary Institution of Science Kazan Scientific Center of the Russian Academy of Sciences, 1995-196 p. [in Russian]
7. Kondratenko P. S. Teoreticheskie osnovy gidrodinamiki i teploperenosa [Theoretical Foundations of Hydrodynamics and Heat Transfer] / P. S. Kondratenko. Moscow: Nuclear Safety Institute of the Russia Academy of Sciences, 2003. 68 p. [in Russian] Gidrodinamika: ucheb. Posobie dlja studentov nematematich-eskikh fakul'tetov [Hydrodynamics: A Manual for Students of Non-Mathematical Faculties] / A. B. Mazo, K. A. Potashev. - Kazan: Kazan University, 2013. - 2nd Edition. - 128 p. [in Russian]
8. Gidrodinamika: ucheb. Posobie dlja studentov nematematicheskikh fakul'tetov [Hydrodynamics: A Manual for Students of Non-Mathematical Faculties] / A. B. Mazo, K. A. Potashev. - Kazan: Kazan Univer-sity, 2013. - 2nd Edition. - 128 p. [in Russian]
9. Van Dyke M. Al'bom techenijj zhidkosti i gaza [Album of Fluid Motion] / M. Van Dyke. Moscow: Mir, 1986-p. 84, fig. 139-140 [in Russian]