ОЦЕНКА СОСТОЯНИЯ ОБЪЕКТА КОНТРОЛЯ МЕТОДОМ е-ОБЛАСТЕЙ

Сучкова Л.И.

Кандидат технических наук, доцент, ФГБОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова»

ОЦЕНКА СОСТОЯНИЯ ОБЪЕКТА КОНТРОЛЯ МЕТОДОМ -ОБЛАСТЕЙ

Аннотация

В статье описан итерационный метод оценки параметров модельной функции квазидетерминированного сигнала в предположении об интервальном характере области значений функции сопровождения. Предложено по допустимой области значений параметров модельной функции осуществлять оценку состояния объекта контроля в информационно-измерительных и управляющих системах.

Ключевые слова: модельная функция, пространство параметров,  оценка параметров.

Suchkova L.I.

PhD in Technical Sciences, assosiate professor, Altay State Technical University

ESTIMATION OF THE OBJECT STATE OF THE CONTROL BY MEANS OF THE -AREAS METHOD

Abstract

In paper the iterative method of an estimation of parametres of modelling function a quasidetermined signal in the supposition about interval character of a range of values of function of support is described. It is offered to carry out on admissible range of values of parametres of modelling function an estimation of a condition of object  of the control in informational-measuring and controlling systems.

Кeywords: modelling function, space of parametres, estimation of parametres.

Состояние объекта контроля оценивается, как правило, путем анализа сигналов с первичных измерительных преобразователей. Будем считать, что сигнал является в общем случае функцией пространственно-временных координат r^Т={x,y,z,t} и вектора параметров 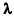. Область координат разбита на множество доменов DM={dm_q}, |DM|=Q, в каждом из которых сигнал характеризуется своей моделью поведения. Для границ каждого домена dm_q выполняется условие интервальности, согласно которому область определения каждой границы D задана не жестко, а может варьироваться в пределах интервалов неопределенности по каждому измерению вектора r. Пусть с учетом погрешностей измерений и влияния случайных факторов модель реального сигнала в каждом домене q имеет вид:

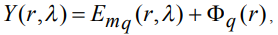                                                     (1)

где 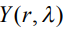 - наблюдаемая реализация сигнала, 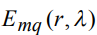- определенная с точностью до параметров модельная функция, описывающая сигнал, с номером типа m из группы функций  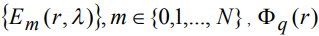- функция сопровождения. Аналитический вид функции сопровождения  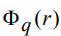неизвестен, однако область ее значений ограничена в силу ограниченности амплитуды реального сигнала. Рассмотрим случай, когда область значений функции сопровождения принадлежит интервалу 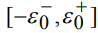, где 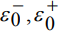 - неотрицательные величины, для которых выполняются соотношения 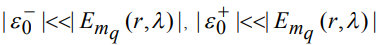. Ансамбль  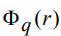образует слой неопределенности в окрестности модельной функции, толщина которого в общем случае может зависеть от r. Основным требованием к модельной функции является непрерывность и простота  вычисления в реальном времени на устройстве с ограниченными вычислительными возможностями. Для компонент вектора 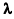в общем случае не выполняется условие независимости, и их интервальные оценки представляют собой область в пространстве параметров, которая должна изменяться в процессе обработки данных реализации сигнала.

Метод нахождения интервальных оценок параметров 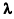при условии ограниченности области значений функции сопровождения Ф_q(r) будем реализовывать как итерационную процедуру, на каждом шаге которой осуществляется уточнение границ области допустимых значений интервальных оценок в пространстве параметров и сравнение этой области с областью значений параметров, соответствующих либо нештатной ситуации на объекте контроля, либо его штатному состоянию.

Для простоты вектор r представим единственной временной компонентой t, что не является принципиальным ограничением. Определение области L допустимых текущих интервальных значений параметров 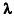осуществляется в соответствии с типом модельной функции. Для простоты изложения метода возьмем линейную модельную функцию .

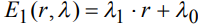На первом шаге метода по реализации сигнала в точках r=0 и r=dr с учетом области значений функции сопровождения вычисляется интервал для параметра 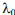, так как согласно типу модельной функции параметр  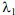при r=0 не влияет на ее значение. При этом верхняя 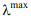и нижняя 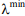границы оценки параметра 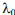равны

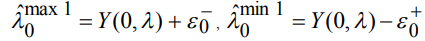                            (2)

Цифра в верхнем индексе параметра соответствует номеру итерации алгоритма. Оценки верхней и нижней границ параметра 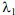зависят от значений параметра 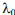,  поэтому будем вычислять оценки параметра 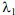в точках, где параметр 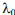принимает минимально и максимально возможные значения (рисунок 1):

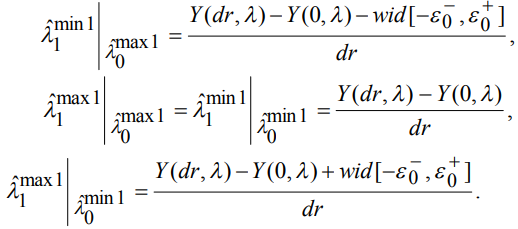                         (3)

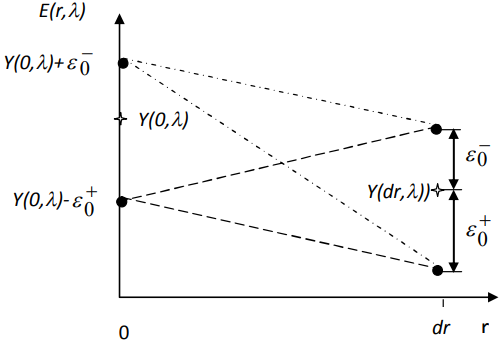
Рис. 1 - Оценка параметров модельной функции 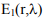на первой итерации метода e-областей

Вычисленные по формулам (2) и (3) интервальные оценки компонент вектора параметров 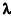формируют в пространстве параметров четырехугольник с вершинами, соответствующими минимальным и максимальным значениям параметров. Будем называть область допустимых интервальных оценок компонент вектора параметров при наложенных ограничениях на область изменения функции сопровождения Ф(r) 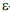-областью. Обозначим 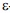-область, полученную на первой итерации работы алгоритма через ОЕ₁, она же на первом шаге будет результирующей областью OR допустимых значений параметров.

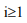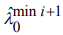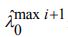На последующих шагах алгоритма по реализации сигнала в точках r=i*dr и r=(i+1)*dr для по формулам (4) вычисляются нижняя и верхняя границы оценок и параметра 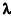₀, а также нижние и верхние границы оценок параметра 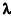₁ для различных значений параметра :

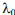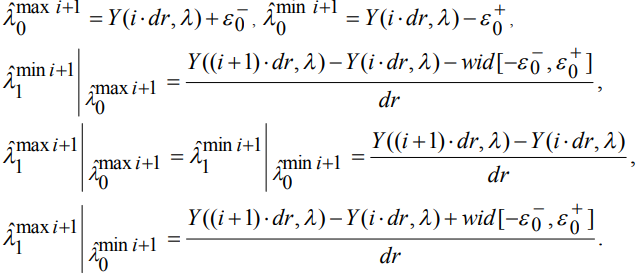 (4)

Вычисленные по (4) значения являются координатами  вершин четырехугольника, образующего 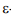-область ОЕ_i+1 в пространстве параметров в соответствии с обходом вершин  против часовой стрелки. Для формирования результирующей 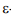-области OR допустимых значений параметров модельной функции на каждой итерации необходимо определять пересечение текущей области OR и 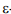-области 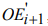, координаты вершин которой получены из координат вершин 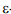-области ОЕ_i+1 путем переноса начала координат из точки (i*dr,0) в точку (0,0). В общем случае задача определения результирующей 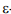-области OR сводится к задаче определения координат вершин многоугольника, являющегося пересечением текущей 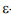-области OR, сформированной по истории реализации сигнала, и 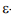-области 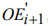. При решении этой задачи использовался метод О’Рурка. На каждом этапе алгоритма происходит уменьшение площади результирующей 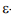-области, что соответствует уточнению интервальных оценок параметров модельной функции и снижению неопределенности по мере появления информации об очередных отсчетах реализации контролируемого сигнала (рисунок 2).

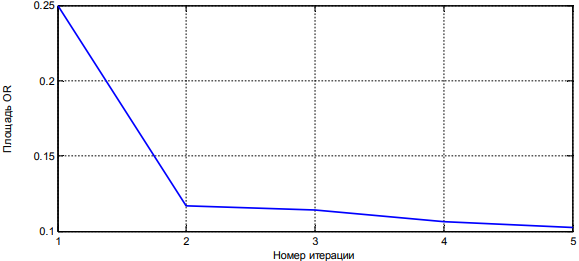
Рис. 2 – Уточнение оценок параметров модельной функции в методе 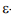-областей

Разработанный метод может быть использован при онлайновом контроле состояний объектов мониторинга в информационно-измерительных и управляющих системах.

Литература

1. Шокин Ю.И. Интервальный анализ. - Новосибирск: Наука, 1981.- 112 с.

2. Калмыков, С.А. Методы интервального анализа / С.А. Калмыков, Ю.И. Шокин, З.Х. Юлдашев. – Новосибирск: Наука, 1986. – 224 с.

3. Шарый С.П. Конечномерный интервальный анализ. – XYZ, 2012. http://www.nsc.ru/interval/Library/InteBooks/SharyBook.pdf (дата обращения 12.02.2013).

4. Сучкова, Л.И. Применение интервальных оценок в приборах и методах контроля для выделения информационных параметров квазидетерминированных сигналов / Л.И. Сучкова, А.Г. Якунин. – Вестник Югорского государственного университета - Вып. 2(21), 2011. - С. 69-81.