ПЕРЕСТРОЙКИ "ЦЕНТР" И "СЕДЛО" В ТЕНЗОРНОМ РАСШИРЕНИИ ЗАДАЧИ ЭЙЛЕРА

Берзин Д.В.

Кандидат физико-математических наук, доцент Финансового университета при Правительстве Российской Федерации, Москва

ПЕРЕСТРОЙКИ "ЦЕНТР" И "СЕДЛО" В ТЕНЗОРНОМ РАСШИРЕНИИ ЗАДАЧИ ЭЙЛЕРА

Аннотация

Особенности типа "центр" и "седло" занимают важное место в теории гамильтоновых систем. В статье рассмотрены соответствующие перестройки на примере тензорного расширения классической задачи Эйлера о движении твердого тела.

Ключевые слова: Гамильтоновы системы, задача Эйлера, тензорные расширения, бифуркации.

Berzin D.V.

Phd in Physics and Mathematics, Associate profesoor, Finanical university under the Government of the Russian Federation, Moscow

BIFURCATIONS "CENTER" AND "SADDLE" IN TENSOR EXTENTIONS OF EULER PROBLEM

Abstract

Peculiarities of the type "center" and "saddle" take an important part in Hamiltonian systems. We consider these bifurcations in tensor extension of classical Euler problem.

Keywords: Hamiltonian systems, Euler problem, tensor extensions, bifurcations,.

Как было отмечено в [1], в теории интегрируемых гамильтоновых систем важным является метод тензорного расширения алгебр Ли, который впервые был предложен В.В.Трофимовым [2], а затем развит А.В.Браиловым [3]. Этот метод, в частности, дает весьма эффективный способ построения инволютивных семейств функций на орбитах коприсоединенного представления групп Ли. Особое место здесь занимает тензорное расширение алгебр Ли посредством фактор-кольца 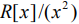. Имеется алгоритм, принадлежащий С.Ж.Такиффу [4] и В.В.Трофимову [2], позволяющий из интегралов и инвариантов для исходной алгебры Ли получить соответствующие интегралы и инварианты для расширенной алгебры. В частности, с помощью этого алгоритма можно из классических и известных систем получать интегрируемые системы с перестройками некомпактных инвариантных подмногообразий.

Известно, что движение трехмерного твердого тела вокруг точки, закрепленной в центре масс, можно описать уравнениями Эйлера для алгебры Ли 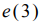 группы движений трехмерного евклидового пространства. Такие системы гамильтоновы на четырехмерных орбитах коприсоединенного представления (диффеоморфных касательному расслоению двумерной сферы) и для полной интегрируемости по Лиувиллю кроме гамильтониана 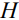указывается еще один (дополнительный) интеграл .

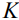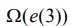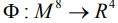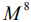В результате тензорного расширения получаем 12-мерную алгебру Ли . Имеем отображение момента , где  – орбита общего положения коприсоединенного представления для тензорного расширения, 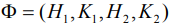, где 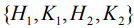– инволютивный относительно скобки Пуассона-Ли набор, получаемый из  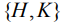при тензорном расширении [5]. Доказывается, что орбита  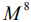общего положения диффеоморфна 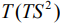, где 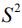– двумерная сфера.

Рассмотрим перестройки типа "центр" (обозначим через "A") и "седло" (обозначим через "B"). В канонических координатах 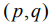 в окрестности начала координат двумерной плоскости они задаются отображениями [6]:

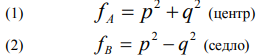
Теорема 1. В результате операции тензорного расширения особенности "центр" и "седло", заданные в локальных канонических координатах 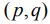 выражениями (1) и (2), перейдут во особенности, определяемые (3) и (4) соответственно:

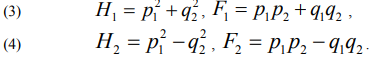
При этом отображения момента 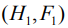 и 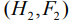 заданы в окрестности точки  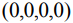в четырехмерном симплектическом пространстве 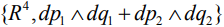. Особенности нулевого ранга (3) и (4) – вырожденные и относятся к типам 14a и 14b соответственно (см. таблицу в конце [7]).

Анализируя отображения момента (3) и (4), мы приходим к следующей теореме.

Теорема 2. Из перестроек A и B при тензорном расширении возникают перестройки T(A), R(A), T(B), R(B) соответственно, которые можно представить так:

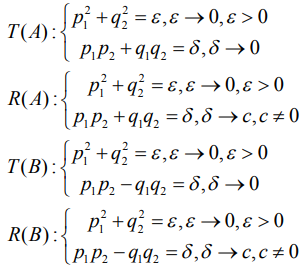
Литература

1. Берзин Д.В. Особенности "центр" и "седло" в тензорных расширениях некоторых гамильтоновых систем / Международный научно-исследовательский журнал, №2 (9), 2013, с. 4

2. Трофимов В.В. Расширения алгебр Ли и гамильтоновы системы / Изв. АН СССР, серия матем., 1983, т.47, № 6, с. 1303-1321

3. Браилов А.В. Инволютивные наборы на алгебрах Ли и расширения кольца скаляров / Вестник МГУ, Сер.1 Математика, механика / 1983, №1, с. 47-51

4. Takiff S.J. Rings of invariant polynomials for a class of Lie algebras. –Trans. Amer. Math. Soc., 1971, V.160, p.249-262

5. Берзин Д.В. Инварианты коприсоединенного представления для алгебр Ли некоторого специального вида / Успехи мат. наук, 1996, т.51, №1, с.141

6.  Eliasson L. Normal forms for Hamiltonian systems with Poisson commuting integrals. Elliptic case / Comment.Math.Helvetici, №65, 1990, p.4-35

7. Lerman L.M., Umanskii Ya.L. Structure of the Poisson action of 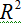on a four-dimensional symplectic manifold / Selecta Mathematica Sovietica, 1987, v.6, №4, p.365-396.