МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОДНОМЕРНОГО ТЕРМОНАПРЯЖЕННОГО (ТЕРМОУПРУГОСТЬ) СОСТОЯНИЕ ЗАЩЕМЛЕННОГО ДВУМЯ КОНЦАМИ СТЕРЖНЯ ПРИ НАЛИЧИИ РАЗНЫХ ИСТОЧНИКОВ ТЕПЛА
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОДНОМЕРНОГО ТЕРМОНАПРЯЖЕННОГО (ТЕРМОУПРУГОСТЬ) СОСТОЯНИЕ ЗАЩЕМЛЕННОГО ДВУМЯ КОНЦАМИ СТЕРЖНЯ ПРИ НАЛИЧИИ РАЗНЫХ ИСТОЧНИКОВ ТЕПЛА
Научная статья
Кенжегулов Б.З.1, Гапуова Т.Б.2, *, Мураткалиева А.Н.3, Рахметов М.Е.4
1, 2, 3, 4 Атырауский государственный университет, Атырау, Казахстан,
* Корреспондирующий автор (tikosh.96[at]mail.ru)
АннотацияНа основе энергетических принципов ориентированный на минимизации полной тепловой энергии упругих деформации в сочетании применении квадратичного конечного элемента с тремя узлами разработан математическая модель защемленного двумя концами стержня, постоянного поперечного сечения в зависимости наличия частичной теплоизоляции, теплового потока и теплообменов.
Ключевые слова: температура, тепловая энергия, тепловой поток, градиент, теплообмен.
MATHEMATICAL MODELING OF ONE-DIMENSIONAL THERMALLY STRESSED STATE (THERMOELASTICITY) OF A ROD FIXED AT TWO ENDS WITH DIFFERENT HEAT SOURCES
Research article
Kenzhegulov B.Z.1, Gapuova T.B.2, *, Muratkaliev A.N.3, Rakhmetov M.E.4
1, 2, 3, 4 Atyrau State University, Atyrau, Kazakhstan
* Corresponding author (tikosh.96[at]mail.ru)
AbstractThe mathematical model of a rod with a constant cross section fixed at both ends is developed depending on the presence of partial thermal insulation, heat flux, and heat exchanges based on energy principles, focused on minimization of total thermal energy of elastic deformations combined with the use of a quadratic finite element with three nodes.
Keywords: temperature, heat energy, heat flow, gradient, heat transfer.
В этой статье рассматривается тестовые задачи нахождения поля рапределения температуры, частично теплоизолированного стержня защемленного двумя концами. В данной задаче стержень ограниченной длины L(см.), площадь поперечного сечения F( ) постоянна по длине, боковая поверхность стержня частично-теплоизолирована. Стержень жестко защемлён обоими концами и имеет цилиндрическую форму (см. рисунок 1).
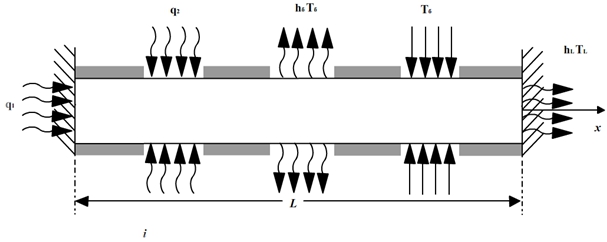
Рис. 1 — Стержень под влиянием разного рода источников тепла и жестко защемлён обоими концами
Под влиянием такого разного рода источников тепла, происходит распределение поля температуры по длине стержня по определенным закономерностям. Эти закономерности можно найти методом минимизации функционала тепловой энергии по значением температуры в узловых точках и методом конечных элементов. Данный стержень дискретизируем квадратичными конечными элементами с тремя узлами. Для каждого элемента напишем специальный функционал, выражающий тепловую энергию [1].
Вариант-1. По площади поперечного сечения левого конца подведен тепловой поток ![]() , а боковая поверхность конечного элемента теплоизолирована. Пусть на правом конце точка k будет внутренней точкой (см. рисунок 2).
, а боковая поверхность конечного элемента теплоизолирована. Пусть на правом конце точка k будет внутренней точкой (см. рисунок 2).

Рис. 2 – Конечный элемент с подведенным на площадь поперечного сечения левого конца тепловым потоком q
Поле распределения температуры по длине такого стержня аппроксимируем как кривую второго порядка проходящей через три точки в участке ![]() будет [5]
будет [5]
![]() (1.1)
(1.1)
где ![]() - функции формы квадратичного конечного элемента с тремя узлами, которые имеют следующее выражение
- функции формы квадратичного конечного элемента с тремя узлами, которые имеют следующее выражение
![]() (1.2)
(1.2)
где ![]() - значение температуры соответствующие точкам элемента
- значение температуры соответствующие точкам элемента ![]() . Пользуясь (1.1.1) и (1.1.2) определим градиент температуры [2, C. 33]
. Пользуясь (1.1.1) и (1.1.2) определим градиент температуры [2, C. 33]
![]() (1.3)
(1.3)
где ![]() производные, которые выражаются через формулы [10], [11]
производные, которые выражаются через формулы [10], [11]
![]() (1.4)
(1.4)
Вид функционала, выражающий тепловую энергию будет следующим [2, C.40]
![]() (1.5)
(1.5)
Здесь V – объем элемента, ![]() - площадь поперечного сечения соответствующая точке
- площадь поперечного сечения соответствующая точке ![]() левого конца элемента. Здесь подставляя соотношение (1.3) и пользуясь выражениям (1.4) на (1.5) можно записать следующим образом [1]
левого конца элемента. Здесь подставляя соотношение (1.3) и пользуясь выражениям (1.4) на (1.5) можно записать следующим образом [1]
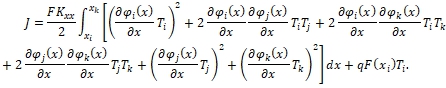 (1.6)
(1.6)
Из—за того, что на участке будет ![]() . Здесь учитывая то, что
. Здесь учитывая то, что ![]() длина данного конечного элемента, интеграл
длина данного конечного элемента, интеграл ![]() можно записать в виде
можно записать в виде ![]() , тогда соотношение (1.5) можно записать в таком виде [2]:
, тогда соотношение (1.5) можно записать в таком виде [2]:
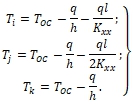 (1.8)
(1.8)
где ![]() - коэффициент теплообмена материала элемента стержня с окружающей средой площади поперечного сечения левого конца, а
- коэффициент теплообмена материала элемента стержня с окружающей средой площади поперечного сечения левого конца, а ![]() температура окружающей среды, значение коэффицента теплопроводности
температура окружающей среды, значение коэффицента теплопроводности ![]() ).
).
Вариант-2. Через площадь поперечного сечения левого конца теплоизолированного по боковой поверхности конечного элемента происходит теплообмен с окружающей средой (см. рисунок 3)
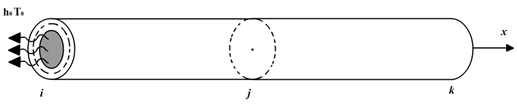
Рис. 3 – конечный элемент с площадью поперечного сечения левого конца, где происходит теплообмен с окружающей средой
Здесь коэффициент теплообмена материала элемента стержня с окружающей средой площади поперечного сечения левого конца будет ![]() , а температура окружающей среды
, а температура окружающей среды ![]() . Тогда для такого конечного элемента вид функционала, выражающий тепловую энергию, будет следующим [1]
. Тогда для такого конечного элемента вид функционала, выражающий тепловую энергию, будет следующим [1]
Вариант-3. Через боковую поверхность и через площадь поперечного сечения соответствующей любой конечной точке конечного элемента происходит теплообмен с окружающей средой. Коэффициент теплообмена с окружающей средой через боковую поверхность будет ![]() , а температура окружающей среды боковой поверхности
, а температура окружающей среды боковой поверхности ![]() (см. рисунок 4).
(см. рисунок 4).
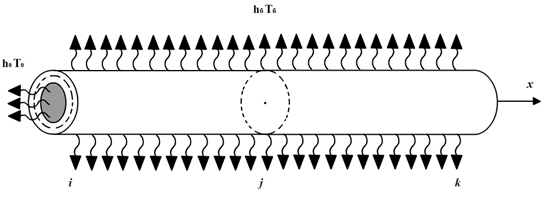
Рис. 4 — Конечный элемент где происходит теплообмен с окружающей средой
Тогда для такого элемента вид функционала, выражающий тепловую энергию, будет следующим [6]
![]() (3.1)
(3.1)
где ![]() площадь боковой поверхности элемента. Но здесь надо учитывать, что
площадь боковой поверхности элемента. Но здесь надо учитывать, что ![]() . Здесь П - периметр поперечного сечения стержня. Тогда соотношение (1.7) можно заново записать следующим образом
. Здесь П - периметр поперечного сечения стержня. Тогда соотношение (1.7) можно заново записать следующим образом
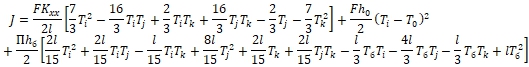 (3.2)
(3.2)
Вариант - 4. Через площадь поперечного сечения левого конца происходит теплообмен с окружающей средой. На боковую поверхность элемента подведен тепловой поток q, (Вт/см2) (см. рисунок 5) [1].
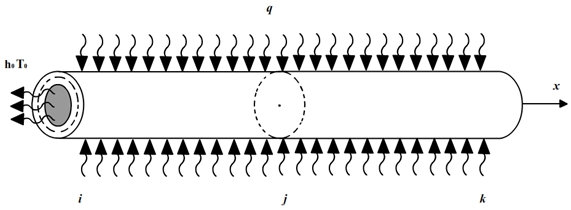
Рис. 5 – Конечный элемент с подведенным на боковую поверхность тепловым потоком q
Тогда для такого элемента вид функционала, выражающий тепловую энергию будет следующим [6]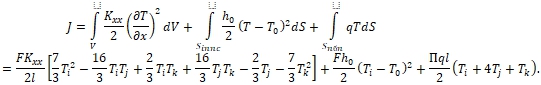 (4.1)
Вариант - 5. На площадь поперечного сечения соответствующей точке i левого конца подведен тепловой поток q1, (Вт/см2), а на боковую поверхность q2, (Вт/см2). Пусть на правом конце точка k будет внутренней точкой (см. рисунок 6) [1].
(4.1)
Вариант - 5. На площадь поперечного сечения соответствующей точке i левого конца подведен тепловой поток q1, (Вт/см2), а на боковую поверхность q2, (Вт/см2). Пусть на правом конце точка k будет внутренней точкой (см. рисунок 6) [1].
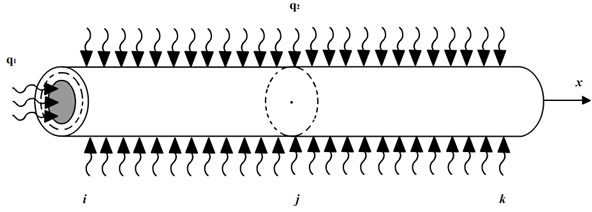
Рис. 6 – Конечный элемент с подведенным на площадь поперечного сечения левого конца тепловым потоком q1 , а на боковую поверхность q2
Для такого конечного элемента вид функционала, выражающий тепловую энергию, будет следующим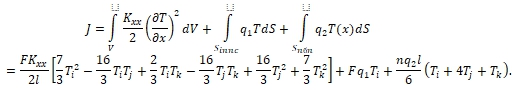 (5.1)
Вариант - 6. На площадь поперечного сечения соответствующей точке i подведен тепловой поток а по боковой поверхности происходит теплообмен с окружающей средой. Здесь коэффицент теплообмена с окружающей средой будет , а температура окружающей среды (см. рисунок 7).
(5.1)
Вариант - 6. На площадь поперечного сечения соответствующей точке i подведен тепловой поток а по боковой поверхности происходит теплообмен с окружающей средой. Здесь коэффицент теплообмена с окружающей средой будет , а температура окружающей среды (см. рисунок 7).
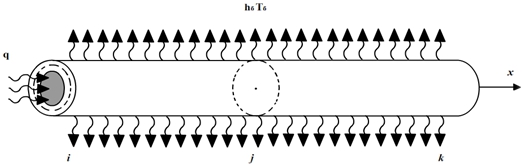
Рис. 7 – Конечный элемент с подведенным на площадь поперечного сечения левого конца тепловым потоком q, а по боковой поверхностью происходит теплообмен с окружающей средой
Тогда для такого конечного элемента вид функционала, выражающий -тепловую энергию, будет следующим [7], [8], [9].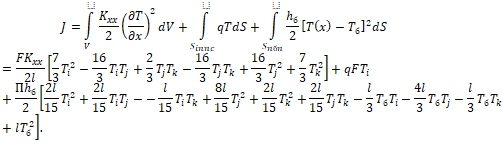 (6.1)
(6.1)
Итак, на основе использования функционала тепловой энергии, а также при использовании аппроксимации теплового поля в стержне конечными элементами в форме кривых 2-го порядка, проходящих через 3 точки по длине стержня, и по температуры которые заданы на узловых точках записывается математическая модель одномерного термонапряженного состояния защемленного двумя концами стержня при наличии разных источников тепла. Рассматривается 6 различных вариантов подведения тепла и теплообмена с внешней средой и соответствующий функционал тепловой энергии.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Кенжегулов Б.З. «Численное моделирование многомерных температурных и одномерных нелинейных термомеханических процессов в жаропрочных сплавах» Монография. ISBN 9965-640-98-Х / Кенжегулов Б.З. Издательство «АтГУ им. Х.Досмухамедова», 2013г.– 326 с.
- Кудайкулов А. Математическое (конечно-элементное) моделирование прикладных задач распространения тепла в одномерных констукционных элементах / Кудайкулов А. – Туркестан, 2009 – 168 с.
- Химушин Ф.Ф. Жаропрочные стали и сплавы. 2-ое переработанное и дополнительное издания / Химушин Ф.Ф. М.: Металлургия, 1969г.-749с.
- Ноздрев В.Ф. Курс термодинамики / Ноздрев В.Ф. Из-во Мир, М.: 1967г.-247с.
- Сегерлинд Л. Применение метода конечных элементов / Сегерлинд Л. Из-во Мир, М.:1979г-392с.
- Зенкевич О. Метод конечных элементов в технике / Зенкевич О. М.: Мир, 1975г.
- Писаренко Г.С. Сопротивление материалов. "Вища Школа" / Писаренко Г.С. Киев, 1973г.-672с.
- Тимошенко С.П. Теория упругости / Тимошенко С.П., Гудьяр Дж.Н. Из-во Мир, «Наука», М.: 1975г.-575с.
- Бергер И.А. Прочность. Устойтивость. Колебания. Том-1 / Бергер И.А., Пановко Я.Г. М.: Машиностроение, 1698г.-56с.
- Эльсгольц Л.Э. Дифференциальное уравнения и вариационное исчисление./ Эльсгольц Л.Э. Из-во Наука, М.: 1969г.-424с.
- Кенжегулов Б.З. «Математическое моделирование исследования термонапряженного в состояния стержня из жаропрочного сплава» / Кенжегулов Б.З., Ж.Д.Мухтаргалиева, Т.Б.Гапуова // Атырауский государственный университет им. Х.Досмухамедова, г. Атырау, Республика Казахстан, Вестник №3(50) 21.11.2018 стр.116
Список литературы на английском языке / References in English
- Kenzhegulov B.Z. Chislennoye modelirovaniye mnogomernykh temperaturnykh i odnomernykh nelineynykh termomekhanicheskikh protsessov v zharoprochnykh splavakh [Numerical modeling of multidimensional temperature and one-dimensional nonlinear thermomechanical processes in heat-resistant alloys. Monograph.] / Kenzhegulov B.Z. ISBN 9965-640-98-X. Publishing house “AtSU named after H. Dosmukhamedov, 2013 – 326 p. [in Russian]
- Kudaikulov A. Matematicheskoye (konechno-elementnoye) modelirovaniye prikladnykh zadach rasprostraneniya tepla v odnomernykh konstuktsionnykh elementakh [Mathematical (finite-element) modeling of applied problems of heat distribution in one-dimensional structural elements] / Kudaikulov A. – Turkestan, 2009 – 168 p. [in Russian]
- Himushin F.F. Zharoprochnyye stali i splavy. 2-oye pererabotannoye i dopolnitel'noye izdaniya [Heat resistant steels and alloys. 2nd edition] / Himushin F.F. M.: Metallurgy, 1969. – 749 p. [in Russian]
- Nozdrev V.F. Kurs termodinamiki [Course of thermodynamics] / Nozdrev V.F. Mir. Moscow: 1967 – 247 p. [In Russian]
- Segerlind L. Primeneniye metoda konechnykh elementov [Application of finite element method] / Segerlind L. M.: Mir. – 1979 – 392 p. [in Russian]
- Zenkevich O. Metod konechnykh elementov v tekhnike [Finite element method in engineering] / Zenkevich O. M.: Mir – 1975. [in Russian]
- Pisarenko G.S. Soprotivleniye materialov [Resistance of materials] / Pisarenko G.S. "Vishcha Shkola", Kiev, 1973. – 672 p. [in Russian]
- Timoshenko S.P. Teoriya uprugosti [Theory of elasticity] / Timoshenko S.P., Goodyar J.N. M.: Mir., "Nauka", M.: 1975. – 575 p. [in Russian]
- Berger I.A. Prochnost'. Ustoytivost'. Kolebaniya [Strength. Sustainability. Fluctuations. Vol. 1] / Berger I.A., Panko Ya.G. M.: Mechanical Engineering, 1698. – 56 p. [in Russian]
- Elsgolts L.E. Differentsial'noye uravneniya i variatsionnoye ischisleniye [Differential equations and calculus of variations] / Elsgolts L.E. Nauka, Moscow: 1969 – 424 p. [in Russian]
- Kenzhegulov B.Z. Matematicheskoye modelirovaniye issledovaniya termonapryazhennogo v sostoyaniya sterzhnya iz zharoprochnogo splava [Mathematical modeling of study of thermally stressed state of rod of heat-resistant alloy] / Kenzhegulov B.Z., Zh.D. Mukhtargalieva, T.B. Gapuova // Atyrau State University. H. Dosmukhamedova, Atyrau, Republic of Kazakhstan, Bulletin No. 3 (50) 11/21/2018 – P.116 [in Russian]
