ГЕОДЕЗИЧЕСКИЙ УГОЛ И ТЕХНОЛОГИЯ ВРАЩАТЕЛЬНЫХ ДВИЖЕНИЙ

ГЕОДЕЗИЧЕСКИЙ УГОЛ И ТЕХНОЛОГИЯ ВРАЩАТЕЛЬНЫХ ДВИЖЕНИЙ

Научная статья

Кораблев Г.А. *

Ижевская государственная сельскохозяйственная академия, Ижевск, Россия

* Корреспондирующий автор (korablevga[at]mail.ru)

Аннотация

Геометрически - геодезический угол, это угол между осью вращения и вектором вращения. Физически – в стационарной системе он может определяться через тангенс угла треугольника, в котором его катеты являются составляющими корпускулярно-волнового процесса.  Получены уравнения функциональных зависимостей в кинетике структурных взаимодействий некоторых макро- и микросистем (в том числе для гравитации). Даются уравнения метаматематической связи между «золотым соотношением» и геодезическим углом, а так же с другими фундаментальными величинами. Применительно к техническим характеристикам египетских пирамид показано как их пропорции соответствуют правилу «золотого соотношения».

Ключевые слова: Геодезический угол, «золотое соотношение», стационарное состояние систем, египетские пирамиды, корпускулярно-волновые процессы, гравитация. 

GEODESIC ANGLE AND ROTATIONAL MOTION TECHNOLOGY

Research article

Korablev G.A. *

Izhevsk State Agricultural Academy, Izhevsk, Russia

* Corresponding author (korablevga[at]mail.ru)

Abstract

From the point of view of geometry, the geodesic angle is the angle between the axis of rotation and the rotation vector. From the point of view of physics, it can be determined through the tangent of the angle of the triangle in a stationary system, where its legs are the components of the wave-corpuscle process. The equations of functional dependencies are obtained in the kinetics of structural interactions of some macro- and micro-systems (including for gravity). Equations of the meta-mathematical relationship between the “golden ratio” and the geodesic angle are given, as well as with other fundamental quantities. It is shown how the proportions of the Egyptian pyramids correspond to the “golden ratio” rule in terms of their technical characteristics.

Keywords: Geodesic angle, “golden ratio,” stationary condition of systems, Egyptian pyramids, wave-corpuscle processes, gravity.

Введение

В технологии вращательных движений для описания их механизма используют кинематические, динамические и угловые параметры. Из них важное значение имеет так называемый геодезический угол (φ), который идентифицируется на основе законов дифференциальной геометрии [1], [2], [3]. Практическое применение он получил, например, в методике расчетов армирования оболочек вращения при изготовлении цилиндрических корпусов космических летательных аппаратов [4], [5].

По этой методике цилиндрическая оболочка корпуса армируется по геодезической линии. «Геодезическая линия - кривая определенного типа, обобщение понятия - прямая для искривленных пространств» [2]. На круговом цилиндре – это винтовые линии, которые дают кратчайшее расстояние между точками на поверхности вращения.

Если намотка полимерных нитей на основу аппарата идет по геодезической линии, то угол между осью вращения и вектором намотки называется геодезическим углом, который равен 54°44´=54,733° [4], [5] – рисунок 1. Известно, что под этим же углом работает тутовый шелкопряд при намотке естественной вискозной нити на основу. Такой же принцип используется и в сельскохозяйственной технологии например, при намотке льняных нитей на основу. Не исключено, что это правило выполняется и в микроструктурных процессах, например при раскручивании или закручивании спирали молекулы ДНК.

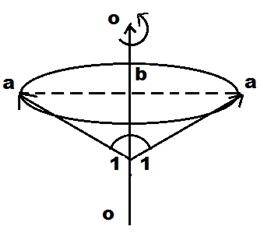
Рис. 1 – Вращательное движение;

где: 1 – геодезический угол (φ), ОО – ось вращения, АО – вектор вращения, АBА – геодезическая линия

 

Целью данного исследования является выявление физического смысла геодезического угла и анализ возможностей его технического применения.

Геодезический угол при конформации стабильных систем

На основе анализа первого начала термодинамики было получено [6]:

1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия, как и приведенная масса, находятся по принципу сложения обратных значений соответствующих величин подсистем. Это – корпускулярный процесс, теоретической концепцией которого может являться энтропия.
2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также соответствующих энергий подсистем. Это – волновой процесс, теоретической концепцией которого может являться негэнтропия.
3. Резонансное стационарное состояние систем выполняется при условии равенства степеней их корпускулярных и волновых взаимодействий. Продукция энтропии в стационарном состоянии полностью компенсируется потоком негэнтропии. Так «при круговом процессе в тепловой машине увеличение энтропии системы от притока теплоты полностью компенсируется уменьшением энтропии при отдаче теплоты, а суммарное значение энтропии равно нулю» [7]:

Эти положения применяются и проявляются во многих микро- и макропроцессах.

Применительно к корпускулярно - волновым процессам условие динамического стационарного состояния есть условие равенства их степеней структурных взаимодействий:

   (1) Математически и графически (по номограммам) стационарное состояние в микросистемах выполняется по уравнению:    (2) Где,  φ - геодезический угол, α - относительная разность энергетических параметров взаимодействующих систем. Аналогично были получены уравнения для числа π:    (3)    (4)

где  g – ускорение свободного падения.

В работах [4], [5] используется понятие разрушающего напряжения при растяжении пластика нити на шаг ее намотки: σ_α – осевое, σ_β – окружное напряжения, которые заменяются пропорциональной им величиной N_α – осевое «усилие» и N_β – окружное «усилие». При этом в кинематике механических систем выполняется:

    (5)

«Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия [4],[5].

Аналогично, для механизма гравитации и сохраняя формализм уравнений (2,5) получено [8].

     (6)

Где,  - электрическая постоянная,

G — гравитационная постоянная,

 – квантовая поправка к гиромагнитному отношению электрона в атоме, которая возможно в данном случае характеризует влияние прецессии движения частиц.

Таким образом, равенство корпускулярных и волновых взаимодействий определяет резонансное стационарное состояние системы. При этом геодезический угол численно определяет соотношение двух катетов прямоугольного треугольника, значения которых через осевые и окружные напряжения характеризуют энергетические зависимости в системе с корпускулярно-волновыми процессами. Это условие  соответствует наиболее оптимальным технологическим вариантам  и широко проявляется в природе, а также во фрактальных системах.

Так еще тысячи лет назад было установлено: «Все явления окружающего нас мира, включая человека и природу интерпретируются китайской медициной, как взаимодействие между двумя началами инь и ян, представляющие собой противоположные аспекты единой действительности» [9]. С позиции этих представлений физиотерапию и рефлексотерапию можно рассматривать как методику выравнивания потенциалов двух проявлений энергетических начал, которыми по современным понятиям являются энтропия и негэнтропия (п.3 исходных положений).

Золотые правила египетских пирамид

«Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений гробниц свидетельствуют, что египетские мастера пользовались соотношением «золотого сечения» при их создании» [10].

«Золотое сечение» или «золотое соотношение» (Ф) – это соотношение, при котором большая величина относиться к меньшей так же как их сумма относиться к большей величине. Ф – иррациональное, алгебраическое число, мера иррациональности которого равна 2. В данных расчетах будет использоваться его приближенное значение Ф=1,618034. Это соотношение широко проявляет себя в природе, в технике, в науке, в искусстве, в биологии и в медицине. Например, в физике для некоторых колебательных систем их  технические характеристики пропорциональны «золотому соотношению».

Можно предположить, что египтяне в период строительства пирамид знали не только о «золотом сечении» и числе π, но имели представления и о геодезическом угле. Но геодезическим углом в пирамиде может быть угол между гранью пирамиды, выполняющей роль вектора «намотки» и той линией основания, которая параллельна земной оси и идет между северной и южной гранью. Очевидно именно по этому пирамиды строились со строгим направлением граней по сторонам света и даже с учетом расположения звезд в определенные времена года.

Такой угол наклона граней в нижней части Ломаной пирамиды составляет 54°34ˈ, то есть только на 10ˈотличается от геодезического угла. Такое совпадение нельзя объяснить случайностью, поэтому эти два многоплановых параметра «золотое соотношение» и геодезический угол должны иметь математическую связь. По аналогии с уравнением (6) получаем:

   (7)

С относительной погрешностью δ=0,13% Совместно с уравнением (6) имеем:    (8)

Уравнения (7,8) дают функциональную зависимость «золотого соотношения» и геодезического угла не только между собой, но и с другими фундаментальными величинами. Поэтому эти уравнения отражают многоплановые проявления и применения данных параметров. Величина 4/3 формально соответствует отношению катетов классического треугольника. Но есть более полное объяснение на основе двух принципов сложения энергетических характеристик подсистем (п.1,2 исходных положений). При сложении двух одноименных и одинаковых энергетических параметров их суммарная величина при корпускулярном взаимодействии увеличивается в два раза, а при волновом – уменьшается в два раза, а их соотношение равно 4. Одна часть этой величины в данном пространственном направлении равна 4/3. Такое число встречается и в других уравнениях, например:

   (9)

где, δ=0.09%

В этом уравнении значение 4/π – характеризует угловое распределение корпускулярно волновых соотношений.

Планировали ли египтяне построить и другие пирамиды с геодезическим углом наклона? Со времени строительства пирамид прошли тысячи лет и точно определить первоначальные размеры и угол наклона сейчас не представляется возможным. Многие из пирамид подверглись значительному разрушению и частично были разобраны [11], [12]. Поэтому угол наклона граней в настоящее время не является геодезическим углом (для большинства пирамид) В данном исследовании он будет обозначаться как α – угол наклона граней пирамид в настоящее время.

Но в технических характеристиках пирамид, хотя и приближенно, должна сохраниться математическая связь между углами φ и α и «золотым соотношением». В таблице 1 рассматриваются наиболее известные пирамиды имеющие правильную пирамидальную форму с углами наклона 51°-52°( для трех пирамид) и углом наклона 43°21´ (для двух пирамид). Так же учтено, что у пирамиды Хефрена имеются грани с разными углами наклона.

Расчеты показали (таб.1), что такая функциональная связь имеет место:

1. Для пирамид с углами наклона грани 51°-52°:

     (10)

где, ˃ среднее значение по трем пирамидам, равное 1,2679.

Так как величина (π/4)Ф=1,2708, то получаем δ=0,22%.

2. Для пирамид с углом наклона 43°21´:

  (11) где δ=0,96%.

Величина (π/4)Ф показывает, как реальные значения  полученные по углу наклона граней в настоящее время соответствуют правилу «золотого соотношения». Наибольшее отклонение от этого правила имеются у пирамиды Микерина. Но эта пирамида только в средние века дважды подвергалась значительному разрушению и воздействию.

Таблица 1 – Углы наклона египетских пирамид

Пирамиды	Хеопса	Хефрена	Микерина	Ломаная	Розовая
α	51°50ˈ	53°10ˈ 52°02ˈ	51°20ˈ	54°34ˈ 43°21ˈ	43°21ˈ
	1,2723	(1,3351=4/3) 1,2815	1,2500	(1,4056) 1,2587	1,2587
˃	1, 2679			1,2587
δ,%	0,22%			0,96%

 

Выводы:

1. Геометрически - геодезический угол, это угол между осью вращения и вектором вращения. Физически – в стационарной системе он может определяться через тангенс угла треугольника, в котором его катеты являются составляющими корпускулярно-волнового процесса.
2. Получено уравнение функциональных зависимостей в кинетике структурных взаимодействий некоторых макро- и микросистем (в том числе для гравитации).
3. Даются уравнения метаматематической связи между «золотым соотношением» и геодезическим углом, а так же с другими фундаментальными величинами.
4. Применительно к техническим характеристикам египетских пирамид показано как их пропорции соответствуют правилу «золотого соотношения».

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Фиников С.П. Дифференциальная геометрия / Фиников С.П. М.:из МГУ, 1961
2. Википедия, Геодезическа линия [Электронный ресурс] URL: https://ru.wikipedia.org/wiki/Геодезическая (дата обращения: 02.10.2019)
3. Пидгайный Ю.М. Механика полимеров / Пидгайный Ю.М., Морозова В.М., Дудко В.А. – 1967.– № 6. – С. 1096-1104.
4. Аюшеев Т.Ю. Геометрические вопросы адаптивной технологии изготовления конструкций намоткой из волокнистых композиционных материалов / Аюшеев Т.Ю. – Улан-Удэ: Изд-во БНЦ СО РАН, 2005. – 212с.
5. Кодолов В.И. Полимерные композиции и технология изготовления из них двигателей летательных аппаратов / Кодолов В.И. Ижевский механический институт, 1992, – 200 с.
6. Korablev G.А. On problematic issues of physical chemistry, Jmest, v6, 2019, pp10320-10324
7. Геворкян Р.Г.Курс общей физики / Геворкян Р.Г., В.В Шепель // Высшая школа, 1972 г., 600 стр.
8. Korablev G.А. On the mechanism of gravitation processes / Korablev G.А. JMEST, v12, 2019, pp705-714.
9. Википедия, Традиционная китайская медицина [Электронный ресурс] URL: https://ru.wikipedia.org/wiki/Традиционная_китайская_медицина (дата обращения: 02.10.2019)
10. Википедия,Египетскиепирамиды [Электронный ресурс] URL:  https://ru.wikipedia.org/wiki/Египетские_пирамиды (дата обращения: 02.10.2019)
11. Lehner M.The Complete Pyramids (неопр.). / Lehner M. - New York: Thames and Hudson(англ.)русск., 1997. — С. 84. — ISBN 978-0-500-05084-2.
12. Щетников А. И.Золотое сечение, квадратные корни и пропорции пирамид в Гизе / Щетников А. И. //Историко-математические исследования. — 13 (48). — 2009. — C. 198—217.

Список литературы на английском языке / References in English

1. Finikov S.P. Differentsialnaya geometriya [Differential Geometry] / Finikov S.P. M.: from Moscow State University, 1961 [in Russian]
2. Vikipediya, Geodezicheskaya liniya [Wikipedia, Geodesic Line] [Electronic resource] URL: https://ru.wikipedia.org/wiki/Геодезическая (accessed: 02.10.2019) [in Russian]
3. Pidgainyi Yu.M. Mekhanika polimerov. [Polymer Mechanics] [Electronic resource] / Pidgainyi Yu.M., Morozova V.M., Dudko V.A. – 1967. – No. 6. – P.1096-1104. [in Russian]
4. Ayusheev T.Yu. Geometricheskie voprosy adaptivnoi tekhnologii izgotovleniya konstruktsii namotkoi iz voloknistykh kompozitsionnykh materialov. [Geometric Issues of Adaptive Technology for Manufacturing Structures by Winding from Fibrous Composite Materials] / Ayusheev T.Yu. – Ulan-Ude: Publishing House of the BSC SB RAS, 2005. – 212 p. [in Russian]
5. Kodolov V.I. Polimernye kompozitsii i tekhnologiya izgotovleniya iz nikh dvigatelei letatelnykh apparatov [Polymer Compositions and Manufacturing Technology of Aircraft Engines] / Kodolov V.I. Izhevsk Mechanical Institute, 1992, - 200 p. [in Russian]
6. Korablev G.А. On problematic issues of physical chemistry / Korablev G.А. Jmest, v 6, 2019, pp10320-10324
7. Gevorkyan R.G. Kurs obshchei fiziki [General Physics Course] / Gevorkyan R.G., V.V Shepel // Higher School, 1972, 600 pp. [in Russian]
8. Korablev G.А. On the mechanism of gravitation processes / Korablev G.А.JMEST, v 12, 2019, pp 705-714.
9. Vikipediya, Traditsionnaya kitaiskaya meditsina [Wikipedia, Traditional Chinese Medicine] [Electronic resource] URL: https://ru.wikipedia.org/wiki/Традиционная_китайская_медицина (accessed: 02.10.2019) [in Russian]
10. Vikipediya, Egipetskie piramidy [Wikipedia, Egyptian Pyramids] [Electronic resource] URL: https://ru.wikipedia.org/wiki/Египетские_пирамиды (accessed: 02.10.2019) [in Russian]
11. Lehner M.The Complete Pyramids  / Lehner M. New York: Thames and Hudson, 1997. — P. 84. — ISBN 978-0-500-05084-2. [in Russian]
12. Shchetnikov A. I. Zolotoe sechenie, kvadratnye korni i proportsii piramid v Gize [Golden Section, Square Roots and Proportions of the Pyramids in Giza] / Shchetnikov A. I. //  Istoricheskoye I matematicheskoye issledovaniye [Historical and Mathematical Research]. – 13 (48). – 2009. – P. 198-217. [in Russian]