УНИТАРНАЯ СТАТИСТИКА БОЗЕ-ЭЕЙНШТЕЙНА-ФЕРМИ-ДИРАКА

Kachevsky D. N.

Chuvash State University   428015 Cheboksary, Russia

Docent, candidate of physical-mathematics sciences

Docent, of faculty of higher mathematics

BOSE-EINSTEIN-FERMI-DIRAC UNITARY STATISTICS

Abstract

The equilibrium statistical distribution of the system of particles with  properties of both bosons and fermions is obtained.  In special cases the distributions is a classical Bose-Einstein and Fermi-Dirac statistics.

Key words: an equilibrium statistic distribution, the Pauli principle.

We solve the problem of the distribution system combinatorics of  identical  particles on the 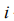 ’s power level in the cells, when the Pauli principle holds : in one cell can be located  no  more than  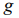identity particles.

The number of  transpositions are equally filled cells, i.e. the number of states  of the 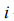’s power level (one state is the certain filling of the fixed  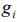by the cells  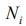identical particles) can be represented by multiple of the numbers of combinations,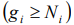

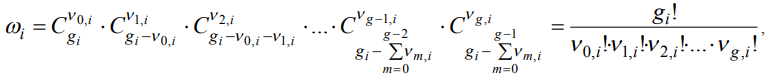                                                                                                                                                                                                                (1)

here 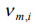 amount of the identically filled cells  of the 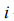’s power level with the number of particles  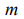in a cell. As a number of cells 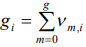, the  one of a values  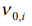 can be expressed through other values,

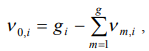                                                                                                                                                                   (2)

and the common amount of particles  of the 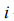’s power level   can be represented in a kind

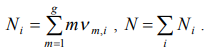                                                                                                                                                  (3)

The common amount of the all transpositions (states) of the system of 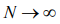 particles appears in a kind 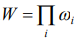, and a corresponding additive size 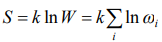, taking into account the Stirling’s approximatons  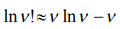we will represent as

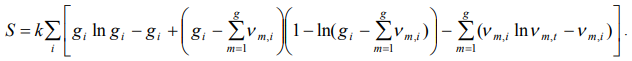                            (4) 

We determine the thermodynamics equilibrium of the system of the 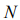 particles as most credible state of the system, corresponding to the maximal amount of the transpositions of the system 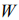, and maximal value of the additive function of the system  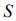entropy of the system (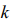- Boltzmann’s constant) on condition of the constancy of the energy of the system of identical particles

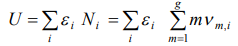                                                                                                                                       (5)

and incurrence  of 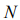 of the particles of the system.

The maximum of function 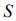 we will search as a conditional extremum deciding equalization the method of multipliers of Lagrange ,

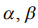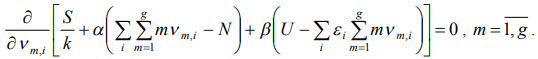                                                   (6)

After the differentiation the system  of the 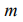 equalizations appears as

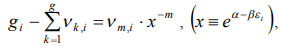                                                                                                                        (7)

and a decision can be written as

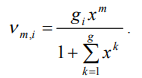                                                                                                                                                              (8)

       With an account (3), distribution of particles on the power levels is

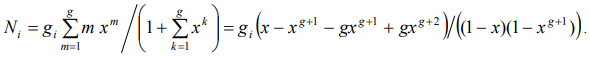                                 (9)

At 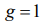  from the left part of the equality we get Fermi-Dirac distribution:

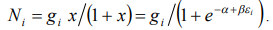                                                                                                                        (10)

Supposing 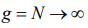, with an account 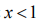, from the right part of the equality we get the Bose-Einstein distribution:

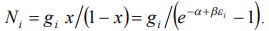                                                                                                                          (11)

The resulting thermodynamic equilibrium distribution of identical particles on energies is a universal statistics with properties of the Bose-Einstein and the Fermi-Dirac statistics.