ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ САМОПОДОБНЫХ СИСТЕМ МЕТОДОМ ЖИДКОСТНОЙ ХРОМОТОГРАФИИ В ВОДЕ

Степанов А.М.¹, Шаповалов Д.С.², Черников А.В.³

¹ORCID: 0000-002—9583-0132, доктор медицинских наук, профессор, ²ORCID: 0000-003-3498-686, кандидат технических наук, Научно-исследовательский институт Экологии Человека и Гигиены Окружающей среды им. А.Н.Сысина, ³ORCID: 0000-0002-9875-0023, доцент, Московский Государственный Университет имени М.В. Ломоносова

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ САМОПОДОБНЫХ СИСТЕМ МЕТОДОМ ЖИДКОСТНОЙ ХРОМОТОГРАФИИ В ВОДЕ

Аннотация

Данная статья посвящена изучению памяти воды за счёт изменения структуры[1] и возможности последующей передачи этих изменений  другим образцам воды. Для реализации этих условий в структуре воды необходимы самоподобные системы.  С целью поиска феномена сам подобия были проведены исследования динамических характеристик времён выхода пиков фракций водной среды методом жидкостной хроматографии высокого давления. Метод высокоэффективной жидкостной хроматографии является одним из прямых методов, способным разделять структурные элементы по размеру и заряду. С целью изучения свойств таких элементов, самопроизвольно образующихся в объёме, нами выбрана для изучения особо чистая вода, называемая «super-Q».

Ключевые слова: хроматография, самоподобные системы, вода, фракции, хроматографические пики.

Stepanov A.M.¹, Shapovalov D.S.², Chernikov A.V.³

¹ORCID: 0000-0002-9583-0132, MD, Professor, ²ORCID: 0000-003-3498-686, PhD. in Engineering, Scientific-Research Institute of Human Ecology and Gigienes Environment n.a. A.N.Sysin, ³ORCID: 0000-0002-9875-0023, Associate Professor, Moscow State University named after M.V. Lomonosov

EXPERIMENTAL STUDIES OF SELF-SIMILAR SYSTEMS IN WATER LIQUID CHROMATOGRAPHY

Abstract

This article is devoted to the study of memory of water due to changes in the structure of [1] and the possibility of onward transmission of these changes to other samples of water. To implement these conditions in the structure of water self-similar systems are needed. In order to find the similarity phenomenon itself were conducted investigating the dynamic characteristics of the output time of the aqueous medium peak fractions by high pressure liquid chromatography, HPLC method is a direct method that can separate the structural elements of size and charge. In order to study the properties of such cells spontaneously formed in the volume we have chosen for the study of highly pure water, which is called «super-Q».

Keywords: chromatography, self-similar systems, the water, fraction, chromatographic peaks

Статистика значений времен выхода хроматографических пиков подчиняется принципу самоподобия.

Исследования проводились в НИИ генетики, центр коллективного пользования. Прибор «Альянс» фирмы Waters c диодо-матричным детектором. ВЭЖХ проводилось в тестовом режиме на длине светового потока 210 нм. Программа обработки данных Enpauer. Скорость потока жидкости 1000 мкл/мин, термостатируемая (30°С) стандартная стальная колонка Atlantis размером 130х4,6 мм с обращённой фазой dC18, 5μm. Элюент — 10% ацетонитрил. Образцы — вода «super-Q» 10 микролитров.

Было проведено исследование более 30 хроматографических процессов, в которых получено 132 значения времен выхода пиков. Полученные значения времен выхода пиков фракций проверялись статистически на нормальность их распределения.

Таблица 1 - Подгонка распределения значений времён выхода пиков на хроматограммах воды super-Q к нормальному.

	Образцы воды super-Q. Распределение Нормальное χ2=181,763; СС=7 (скор.).; р = 0,00000
	Наблюд Частота	Кумул. Наблюд	% наблюд	Кумул %	Ожид. частота	Кумул. Ожид.	% ожид	Кумул.% Ожид.	Наблюд Ожид.
≤ 0	0	0	0,00	0,00	19,49	19,49	14,77	14,77	-19,49
1,0	10	10	7,57	7,57	11,06	30,55	8,37	23,14	-1,06
2,0	44	54	33,33	40,91	13,88	44,43	10,51	33,66	30,12
3,0	46	100	34,85	75,76	15,81	60,25	11,98	45,64	30,18
4,0	5	105	3,79	79,54	16,36	76,61	12,39	58,04	-11,36
5,0	1	106	0,76	80,30	15,36	91,97	11,64	69,68	-14,36
6,0	9	115	6,18	87,12	13,10	105,07	9,92	79,60	-4,10
7,0	2	117	1,51	88,64	10,14	115,21	7,68	87,28	-8,14
8,0	0	117	0,00	88,64	7,12	122,33	5,39	92,67	-7,12
9,0	0	117	0,00	88,64	4,54	126,87	3,44	96,12	-4,54
10,0	0	117	0,00	88,64	2,63	129,50	1,99	98,11	-2,63
11,0	7	124	5,30	93,94	1,38	130,88	1,05	99,15	5,62
12,0	2	126	1,51	95,45	0,66	131,54	0,50	99,65	1,34
13,0	6	132	4,54	100,00	0,28	131,83	0,22	99,87	5,71
< ∞	0	132	0,00	100,00	0,17	132,00	0,13	100,00	-0,17

Как видно из данных, приведенных в таблице 1, значения времён выхода пиков соответствуют нормальному распределению с высокой вероятностью (p<0,000001); χ2=125,916.

Если нанести на график наблюдаемые значения и вычисленные теоретические значения по нормальному распределению, мы получим форму распределения значений в координатах «квантиль-квантиль».

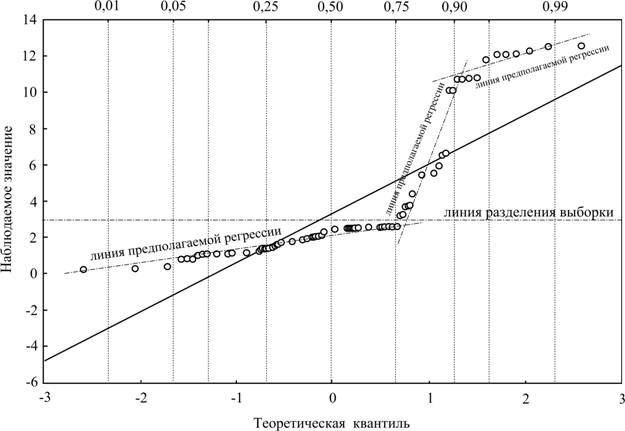
Рис. 1 - График квантиль-квантиль по значениям времени пиков выхода на хроматограммах воды super-Q.  2v*132. Распределение нормальное

Полученный график соответствует уравнению регрессии: tпика = 3,3488+2,7227хтеорет. Однако мы видим, что общая картина распределения значений вокруг линии регрессии не случайна и имеет, по крайней мере, два излома, между которыми мы наблюдаем близкие к прямым участки. Для этих участков, очевидно, можно построить свои линии регрессии, которые будут более точно вычислять теоретические значения квантилей. С этой целью разделим выборку на две подгруппы. Первая подгруппа значений выхода пиков будет занимать область от 0 до 3 минут (нижняя часть графика) и вторая — от 3 до 14 минут (верхняя часть графика).

Просчитаем линию регрессии для первой подгруппы в которой оказалось достаточное количество значений времён выхода пиков (100 значений) и построим соответствующий график.

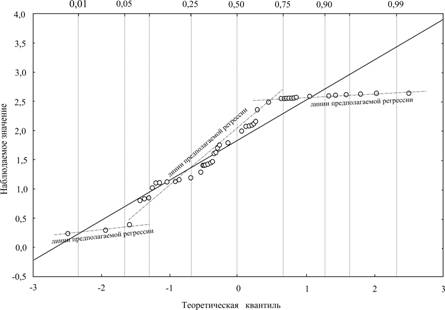
Рис. 2 - График квантиль-квантиль по значениям времени выхода пиков на хроматограммах контрольных образцов первой подгруппы (100). Распределение нормальное. Уравнение регрессии: t = 1,8444+0,6886x.

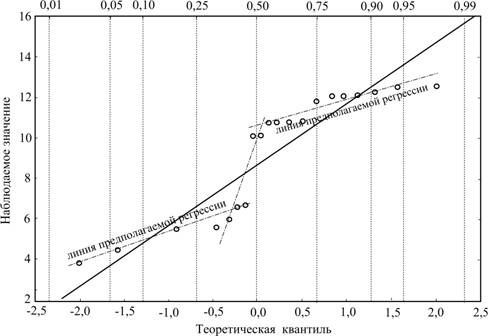
Рис. 3 -  График квантиль-квантиль по значениям времени выхода пиков на хроматограммах контрольных образцов второй группы (28). Распределение нормальное. Уравнение регрессии: t = 8,686+3,0178x.

На всех трёх графиках наблюдается одна и та же картина статистических линейных распределений значений времён выхода пиков в виде самоподобных ломанных линий, которые не теряют своего принципиального строения при уменьшении выборки. Это указывает на голографический принцип самоподобия части и целого.

Для того чтобы убедится что это не зависит от принятой статистической модели распределения — гауссова кривая, построим другую модель распределения статистических характеристик, например, бета-распределение.

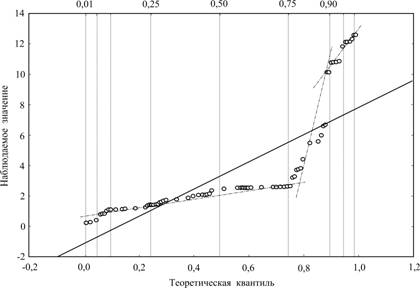
Рис. 4 - График квантиль-квантиль по значениям времени выхода пиков на хроматограммах контрольных образцов 2v*132. Распределение бета (1, 1). у= -1,0993+8,8996х

Как мы видим, структура статистического распределения сохраняется самоподобной. Тоже строение сохраняется при построении графика вероятностном

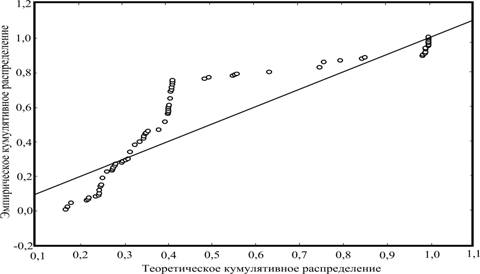
Рис. 5 - График вероятность-вероятность по значениям времени выхода пиков на хроматограммах контрольных образцов (n=132). Распределение нормальное (3,35052; 3,20197).

На всех графиках нормального, бета и других распределений наблюдаются статистически самоподобные структуры распределений времён выхода пиков. Картина не меняется, если мы рассматриваем ту или иную часть выборки. Наращивая объём статистических данных, и повышая точность измерения времени выхода пиков, мы будем получать такие же самоподобные структуры. Это явление говорит нам о функциональном фрактальном строении структур водной среды.

Заключение.

В работе[2,3] была показана возможность воспроизводить водой в окружающую среду действие поля меняющее Рн в пробниках воды. Такое явление возможно, если вода обладает свойством голографического отображения функционального состояния своей среды, т.е. обладает способностью формирования самоподобных структур. Проверка предположения подтвердила наличие самоподобных функциональных структур в исследованиях статистических распределений времён выхода хроматографических пиков водных структур.

Вывод

Вода обладает самоподобными структурами, которые допускают возможность трансляции в окружающее пространство своих функциональных свойств по голографическому принципу, воздействуя на другие водные объекты.

Список литературы / References

1. Зенин С. В. Вода / С. В.Зенин. - М.: 2001.- 48 с.
2. Шаповалов Д. С. Распределение пространственных неоднородностей электромагнитного поля в присутствии источника электромагнитного поля и массивов воды / Д. С.Шаповалов, А. М.Степанов, А. В.Черников // Международный научно-исследовательский журнал – 2016. – № 12 (54) - Часть 3– С.210-215.
3. Schiff М. The Memory of Water. Homeopathy and the battle of ideas in the new science. - Thorons, San Francisco, 1995

Список литературы на английском языке / References in English

1. Zenin S. V. Voda  [Water] / S. V. Zenin. - M .: 2001.- 48 P. [in Russian]
2. Shapovalov D. S. Racpredelenie prostranstwennyx neodnorodnostey elektromagnitnogo polja v prisutstwii istochnika  elektromagnitnogo polja i massiwow wody  [  Distributed spatial inhomogeneities of the electromagnetic field in the presence of an electromagnetic field source and array of water ] / D. S.Shapovalov, A. M.Stepanov, A. V. Chernikov // Mezhdunarodnyj nauchno – issledovatelskyi zhdurnal  [ International Research Journal ].  - 2016. -  № 12 (54) - Part 3 – P. 210-215. [in Russian]
3. Schiff M. The Memory of Water. Homeopathy and the battle of ideas in the new science. - Thorons, San Francisco, 1995.