МЕТОД ИДЕНТИФИКАЦИИ НА ОСНОВЕ МНОГОМЕРНОЙ ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

Кудаев Н.Ю.¹, Елизаров А.И.², Калайда В.Т.³

¹ аспирант; ² кандидат технический наук, доцент; ³ доктор технических наук, профессор, Национальный исследовательский Томский Государственный Университет

МЕТОД ИДЕНТИФИКАЦИИ НА ОСНОВЕ МНОГОМЕРНОЙ ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

Аннотация

В статье предлагается метод идентификации, базирующийся на построении классов объектов, как многомерной функции плотности распределения векторов параметров.

Ключевые слова: идентификация, многомерная функция плотности распределения.

Kudayev N. Y.¹, Elizarov A.I.², Kalayda V.T.³

¹ postgraduate student; ² Candidate of Technical Sciences, associate professor; ³Doctor of Technical Sciences, professor, National Research Tomsk State University

IDENTIFICATION TECHNIQUE BASED ON THE MULTIDIMENSIONAL PROBABILITY DENSITY FUNCTION

Abstract

In this paper we propose a method of identification based on the construction of classes of objects as multidimensional density function parameter vectors.

Keywords: Identification, multidimensional density function.

Идентификация является актуальной проблемой в различных сферах современного общества. Например, идентификация объектов в системах безопасности, в системах мониторинга. На практике, большое количество задач идентификации, решается применительно к изображениям. Предлагаемый метод идентификации на основе многомерной функции плотности распределения подходит для решения задачи идентификации независимо от типа исходных данных.

Для описания классов можно использовать многомерную функцию плотности распределения. В свою очередь каждый объект характеризуется своим вектором параметров (характеристик). Набор таких векторов описывает класс. Дальнейшая задача будет сводиться к отнесению идентифицируемого объекта к одному из известных классов по его набору параметров.

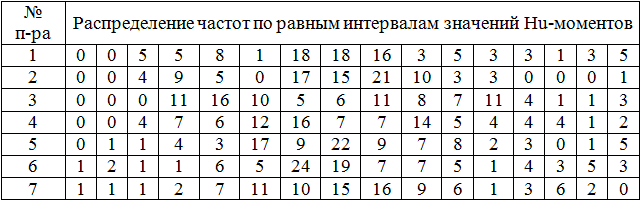
Примем во внимание гипотезу о том, что априори условия получения векторов параметров, описывающих объекты, неизвестны. Следовательно, имеется множество различных векторов, полученных при множестве условий. Группы векторов, полученных при схожих параметрах, образуют множество незивестных распределений. В соотвествии с предельной теоремой можно предположить, что множество векторов параметров является нормальным (то есть описывается многомерной Гауссовской функцией плотности распределения). Это частично подтверждается в работе [1], когда гиперповерхность аппроксимируется полиномом второго порядка. В таблице 1 для одной из выборок векторов параметров изображений, из работ [1] и [2], представлены экспериментальные частоты по равным интервалам.

Таблица 1 -  Экспериментальные частоты характеристик Hu-моментов набора изображений одного класса.

Предположим, что по множеству векторов (наборов параметров) можно построить многомерную нормальную функцию распределения. Числовые характеристики такой функции описываются ковариационной матрицей, которую для упрощения, можно повернуть и сделать диагональной. Полученная диагональная матрица будет содержать на главной диагонали собственные числа исходной матрицы. Для получения собственных чисел используется метод Данилевского. В результате чего матрица приводится к виду Фробениуса. Собственные числа матрицы Фробениуса равны собственным числам исходной ковариационной матрицы [3]. Таким образом, класс изображений описывается значениями средних (мат. ожиданий) и стандартных отклонений для каждой из характеристик. В дальнейшем планируется для получения собственных чисел ковариационной матрицы использовать готовые алгоритмы, входящие в математические пакеты. Это позволит повысить точность и быстродействие вычислений, а также уменьшит затраты на сопровождение этой части алгоритма.

Алгоритм идентификации заключается в принятии решения голосованием о принадлежности изображения к классу. Каждая характеристика вектора параметров идентифицируемого объекта проверяется на вхождение в соответствующий ей интервал . В такой интервал входят 95% всех значений для нормального распределения. При решении реальной задачи, могут возникнуть ситуации, когда несколько характеристик удовлетворяют интервалу, а несколько – нет. Решение принимается голосованием: если больше половины характеристик одного вектора удовлетворяют своим интервалам, то считается, что изображение принадлежит к классу. В противном случае – не принадлежит.

К преимуществам данного метода можно отнести следующее:

• независимость от типа входных данных;
• устойчивость к условиям получения входных данных (слабая зависимость от условий съёмки изображений);
• устойчивость к изменению ориентации и положения идентифицируемого объекта;
• высокая точность метода при достаточном наборе параметров.

Недостатки предлагаемого метода :

• при увеличении количества классов метод чувствителен к информационности выбранных параметров;
• как и для большинства методов идентификации, для более точного описания класса требуется большее количество векторов параметров.

В дальнейших исследованиях предложенный метод будет использоваться для решения задач идентификации личности человека и классификации типов облачности.

 

Литература

1. Калайда, В.Т. Метод опорной гиперповерхности для идентификации изображения лица человека / В.Т. Калайда, А.И. Елизаров // Вычисл. технологии. – 2012. – Том 17, № 5. - С. 65-70.
2. Калайда, В.Т. Идентификация лица человека методом опорной гиперплоскости / В.Т. Калайда, Н.Ю. Губанов // Вычисл. технологии. - 2007. – Том 12, Специальный выпуск №1: Труды отдела проблем информатизации ТНЦ СО РАН. - С. 96-101.
3. Мицель, А.А. Вычислительная математика: учебное пособие /А.А. Мицель// Томск: Томский межвузовский центр дистанционного образования. – 2001. – 228с.

References

1. Kalajda, V.T. Metod opornoj giperpoverhnosti dlja identifikacii izobrazhenija lica cheloveka / V.T. Kalajda, A.I. Elizarov // Vychisl. tehnologii. – 2012. – Tom 17, № 5. - S. 65-70.
2. Kalajda, V.T. Identifikacija lica cheloveka metodom opornoj giperploskosti / V.T. Kalajda, N.Ju. Gubanov // Vychisl. tehnologii. - 2007. – Tom 12, Special'nyj vypusk №1: Trudy otdela problem informatizacii TNC SO RAN. - S. 96-101.
3. Micel', A.A. Vychislitel'naja matematika: uchebnoe posobie /A.A. Micel'// Tomsk: Tomskij mezhvuzovskij centr distancionnogo obrazovanija. – 2001. – 228s.