Сравнение частотных характеристик узлов электрических сетей при различных моделях линейной нагрузки
Сравнение частотных характеристик узлов электрических сетей при различных моделях линейной нагрузки
Аннотация
В современных электрических сетях часто наблюдается повышенный уровень гармонических составляющих токов и напряжений, обусловленных, как правило, нелинейными нагрузками. Как следствие, возникает задача анализа характеристик электрической сети в широком частотном диапазоне. При этом на результаты существенное влияние оказывают выбранные модели отдельных элементов сети. В данной статье представлены результаты сопоставительного анализа частотных характеристик узловых сопротивлений, рассчитанных при представлении линейной нагрузки различными математическими моделями. Показано, что характеристики узловых сопротивлений для различных моделей нагрузки значительно отличаются как по амплитуде, так и по характеру изменения сопротивления в функции частоты. Выбор модели нагрузки также оказывает сильное влияние на резонансные частоты и условия появления резонанса. Для трех моделей обнаружено практическое совпадение резонансных частот в широком диапазоне изменения параметров сети и мощности нагрузки. Выбор модели нагрузки оказывает существенное влияние на частотные характеристики узловых сопротивлений, и это необходимо учитывать при исследовании сети в области частот высших гармоник.
1. Введение
Присутствие высших гармоник в электрических сетях является одной из основных проблем обеспечения качества электроэнергии. Массовое использование выпрямителей, частотно-регулируемых приводов и другой преобразовательной техники приводит к генерации широкого спектра гармоник. При совпадении частот гармоник с собственными частотами сети возникают параллельные и последовательные резонансы, приводящие к значительному увеличению амплитуд напряжений и токов высших гармоник, что оказывает негативное влияние на элементы сети, особенно на батареи конденсаторов. Для оценки возможности возникновения резонансных процессов и выработки мер по их предотвращению необходимо знание частотных свойств электрической сети и ее отдельных элементов. При этом анализ производится в частотном диапазоне от основной гармоники до 40-й либо 50-й гармоники.
Элементы электрической сети в расчетах на частотах высших гармоник обычно представляются математическими моделями в виде схем замещения, параметры которых являются частотно-зависимыми. В литературе представлено множество таких моделей для воздушных и кабельных линий электропередачи, трансформаторов, нелинейных нагрузок. Для линейных нагрузок также предложен ряд моделей. Так, например, широко известна модель СИГРЭ , выведенная в ходе экспериментальных исследований для частотного диапазона от 5-й до 20-й гармоник. Несколько моделей было представлено в и . В рассмотрены семь моделей нагрузки, начиная от простейшей в виде независимого от частоты активного сопротивления и заканчивая моделью СИГРЭ. В рекомендовано представлять линейную НГ в виде последовательной RX-цепочки с параметрами, зависящими от частоты. В для моделирования линейной НГ на частотах гармоник предложено лишь одно выражение, предусматривающее линейное уменьшение проводимости ветви нагрузки с ростом частоты. Разрабатываются и более сложные модели; например, в предложена детализированная модель нагрузки, которая может применяться как для расчета динамических режимов, так и для исследования высших гармоник; она успешно использовалась для изучения процессов в существующей распределительной кабельной сети на частотах гармоник.
Учитывая разнообразие моделей, возникает вопрос о степени совпадения результатов, полученных при представлении элемента сети той или иной моделью. Например, в на примере 68-узловой сети исследовано влияние выбора модели для линий передачи и трансформаторов на уровень гармоник в сети. Установлено, что численные значения существенно различаются между собой, при этом максимальный уровень гармоник достигается при выборе сосредоточенной модели для линий и модели трансформатора без учета скин-эффекта, а минимальный — при выборе модели линии с распределенными параметрами и модели трансформатора, учитывающей скин-эффект как hR, где h — номер гармоники. Для линейных нагрузок разные способы их представления в сети также приводят к различным результатам моделирования, причем попытки исследовать степень этого различия приводят к неоднозначным результатам. В целом, доказано, что сам по себе учет комплексных сопротивлений нагрузок при расчете режимов высших гармоник (по сравнению со случаем, когда этими сопротивлениями пренебрегается) оказывает демпфирующее влияние, снижая расчетный уровень высших гармоник , , . В указывается, что для рассмотренных там моделей нагрузок, несмотря на некоторое различие амплитудно-частотных характеристик, их влияние на АЧХ сопротивлений узлов практически не сказалось, и можно пользоваться любой из этих моделей с равным успехом. В то же время в , отмечается, что выбор модели нагрузки оказывает существенное влияние на величины узловых сопротивлений, в частности возле точки параллельного резонанса; то же самое касается и распространения гармоник в сети , . В на примере 18-узловой тестовой распределительной сети IEEE исследовалось влияние выбора модели нагрузки на результаты расчета распределения высших гармоник. Показано, что для различных моделей нагрузки резонанс наступает на примерно одинаковых частотах, в то время как величины узловых сопротивлений на резонансных частотах существенно различаются: некоторые результаты отличаются от усредненного по всем моделям значения на 50% и более. Однако различные схемы замещения линейной нагрузки имеют совершенно разный характер изменения комплексного сопротивления в функции частоты. Поэтому указанное совпадение резонансных частот, скорее всего, не будет иметь место для других сетей. Тогда возникает вопрос о степени близости резонансных частот и, в несколько более общей постановке вопроса, о совпадении резонансных условий, если линейная нагрузка учитывается с помощью разных моделей.
Таким образом, необходимо дальнейшее исследование частотных свойств электрических сетей при использовании различных моделей нагрузки, с целью устранения отмеченных расхождений в результатах моделирования. Исходя из этого, целью данной работы является сопоставительный анализ частотных характеристик узлов электрической сети при представлении линейной нагрузки различными математическими моделями.
2. Методы и принципы исследования
Для проведения исследования были взяты семь моделей линейной нагрузки из , , , схемы замещения и параметры которых приведены на рис. 1. В расчетных формулах P и Q — активная и реактивная мощность, потребляемые нагрузкой на основной частоте сети (50 Гц), U — номинальное напряжение сети, h — порядковый номер гармоники.
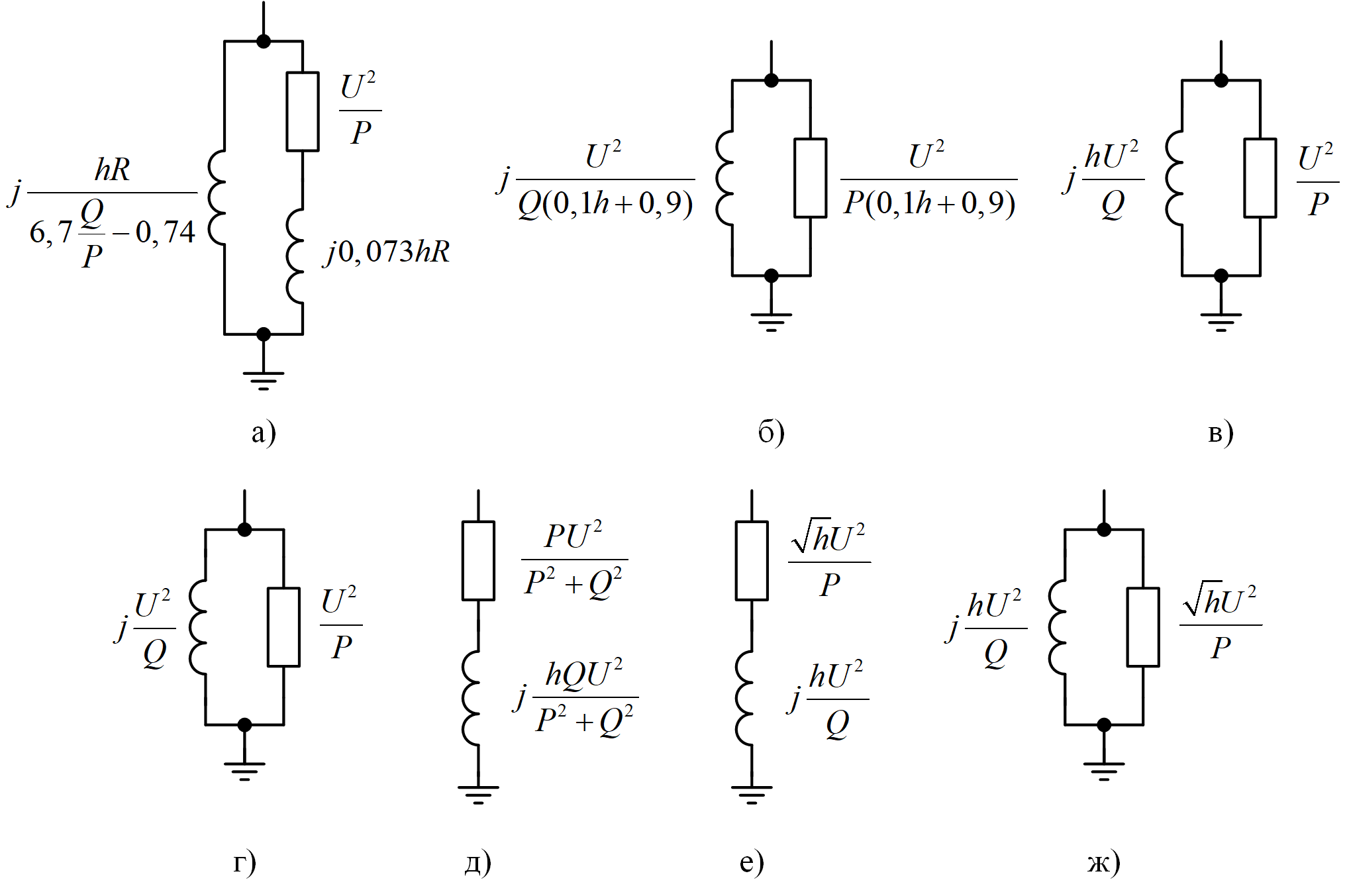
Рисунок 1 - Схемы замещения и параметры моделей линейной нагрузки:
а - модель 1 (СИГРЭ); б - модель 2, в - модель 3; г - модель 4; д - модель 5; е - модель 6; ж - модель 7
Расчеты выполнялись для модельной электрической сети с номинальным напряжением 10 кВ, схема которой представлена на рис. 2.
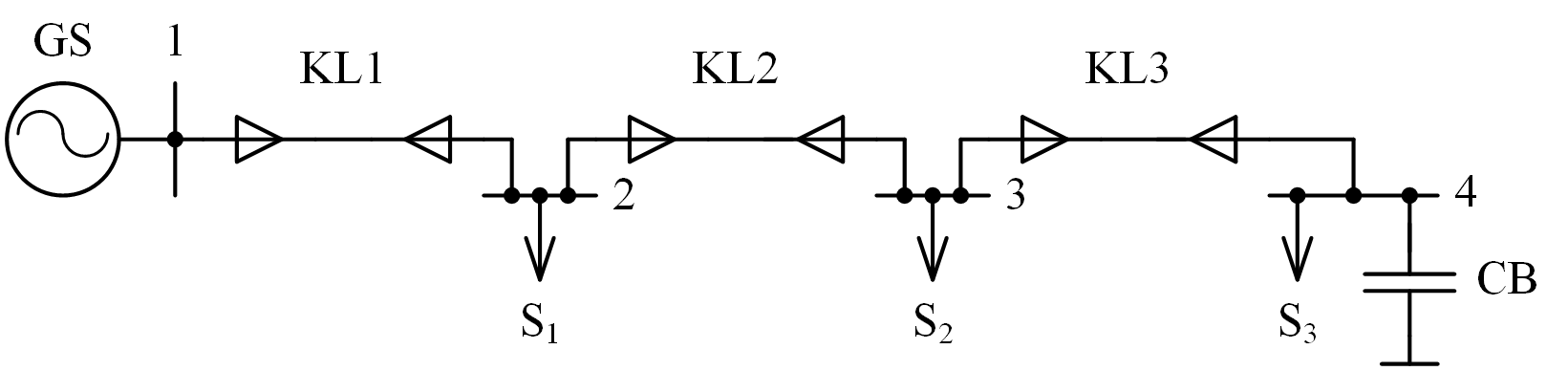
Рисунок 2 - Схема модельной сети
- система GS: мощность короткого замыкания системы SКЗ=200 МВА, отношение R/X=0,2;
- кабельные линии: KL1 длиной 3 км, KL2 и KL3 длиной 2 км, удельные сопротивления на частоте 50 Гц для всех линий: R0=0,124 Ом/км, Х0=0,143 Ом/км, удельная емкость C0=0,357 мкФ/км;
- нагрузки: S1=2+j1 МВА, S2=1+j0,5 МВА. Мощность нагрузки S3 в узле 4 изменялась в ходе исследования, вначале принята равной S3=1+j0,5 МВА;
- батарея конденсаторов CB: мощность 500 квар, затем 1000 квар; в начале исследования отключена.
Анализ частотных свойств сети производился с использованием амплитудно-частотных (АЧХ) и фазочастотных (ФЧХ) характеристик собственных узловых сопротивлений Zу. Частота в расчетах изменялась от 50 до 2500 Гц, что соответствует интервалу от 1-й до 50-й гармоники сетевого напряжения. Шаг изменения частоты составлял 1 Гц. При составлении графиков по горизонтальной оси откладывались не абсолютные значения частот, а соответствующие им порядковые номера гармоник, что более удобно для сопоставления с каноническими гармониками и часто используется в литературе (см., например, , , ).
По схеме рис. 2 была составлена расчетная модель сети, в которой нагрузка представлялась поочередно каждой из схем замещения, приведенных на рис. 1. Кабельные линии учитывались П-образными схемами замещения, питающая система — RX-цепочкой, конденсаторная батарея — емкостным сопротивлением.
3. Основные результаты
На рис. 3 представлены АЧХ и ФЧХ, рассчитанные для узла 4 при исходных данных.
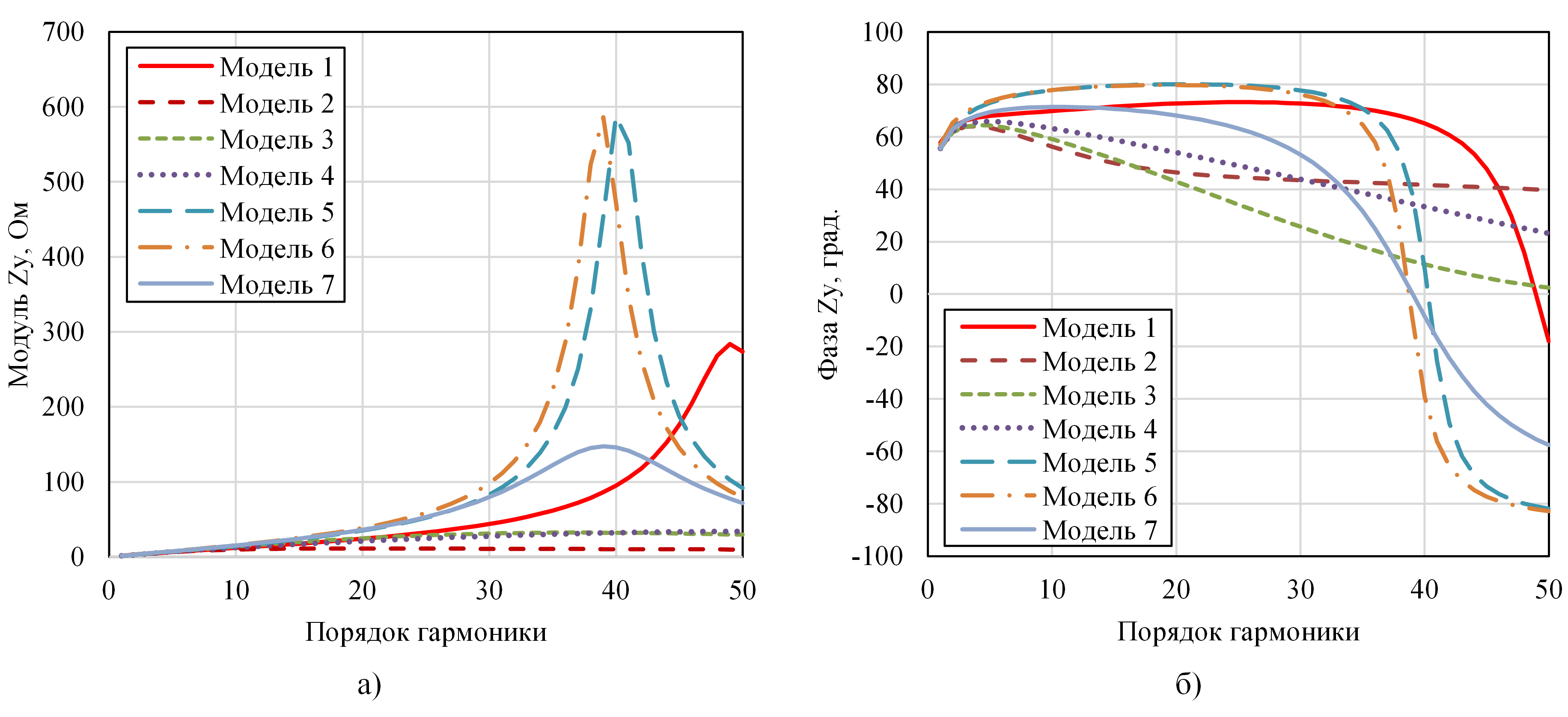
Рисунок 3 - АЧХ (а) и ФЧХ (б) для узла 4 при исходных данных
Были проведены расчеты частотных характеристик при варьировании удельных параметров кабельных линий, их длин, а также мощности короткого замыкания питающей системы как в меньшую, так и в большую сторону относительно исходных величин. Результаты расчетов показали, что в большинстве вариантов при использовании моделей 5, 6 и 7 наблюдался параллельный резонанс, при этом его частота оказывалась в интересующей полосе частот (50-2500 Гц). При использовании остальных моделей резонанса либо вообще не было, либо он был за пределами указанного диапазона. Однако даже и в таких случаях наблюдалось существенное различие характеристик для разных моделей. В качестве примера на рис. 4 приведены АЧХ и ФЧХ для узла 3, рассчитанные для тех же начальных данных, за исключением того, что длины всех линий были приняты равными 1 км. Из рис. 4 видно, что в данном случае резонанса нет, однако различие между наибольшим (для модели 6) и наименьшим (для модели 2) значениями Zу на верхней границе расчетного диапазона достигает 14,8 раза. Если ограничиться диапазоном, в котором существуют наиболее мощные канонические гармоники, часто наблюдающиеся в электрических сетях (до 25-й гармоники, т.е. до частоты 1250 Гц), то в нем различие между характеристиками достигает 3,3 раза. Следует отметить, что характеристики для моделей 5, 6 и 7 здесь также оказались близки между собой: в диапазоне частот до 1250 Гц они различаются по амплитуде не более чем на 5,7%, а на верхней границе расчетного диапазона — не более чем на 11,5%. Аналогичная ситуация с этими моделями наблюдалась и в других узлах подключения нагрузки, во всех расчетных вариантах.
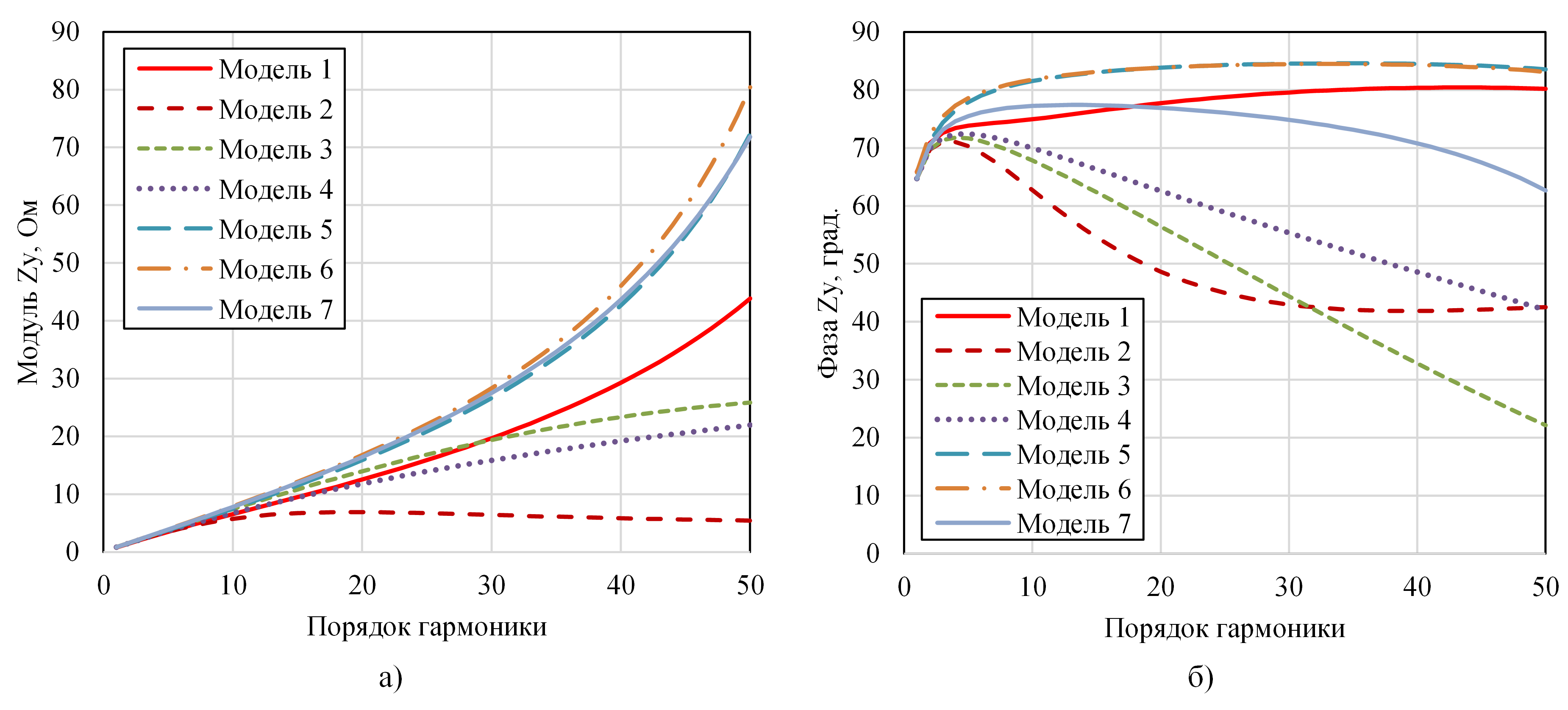
Рисунок 4 - АЧХ (а) и ФЧХ (б) для узла 3 при длинах кабельных линий, равным 1 км
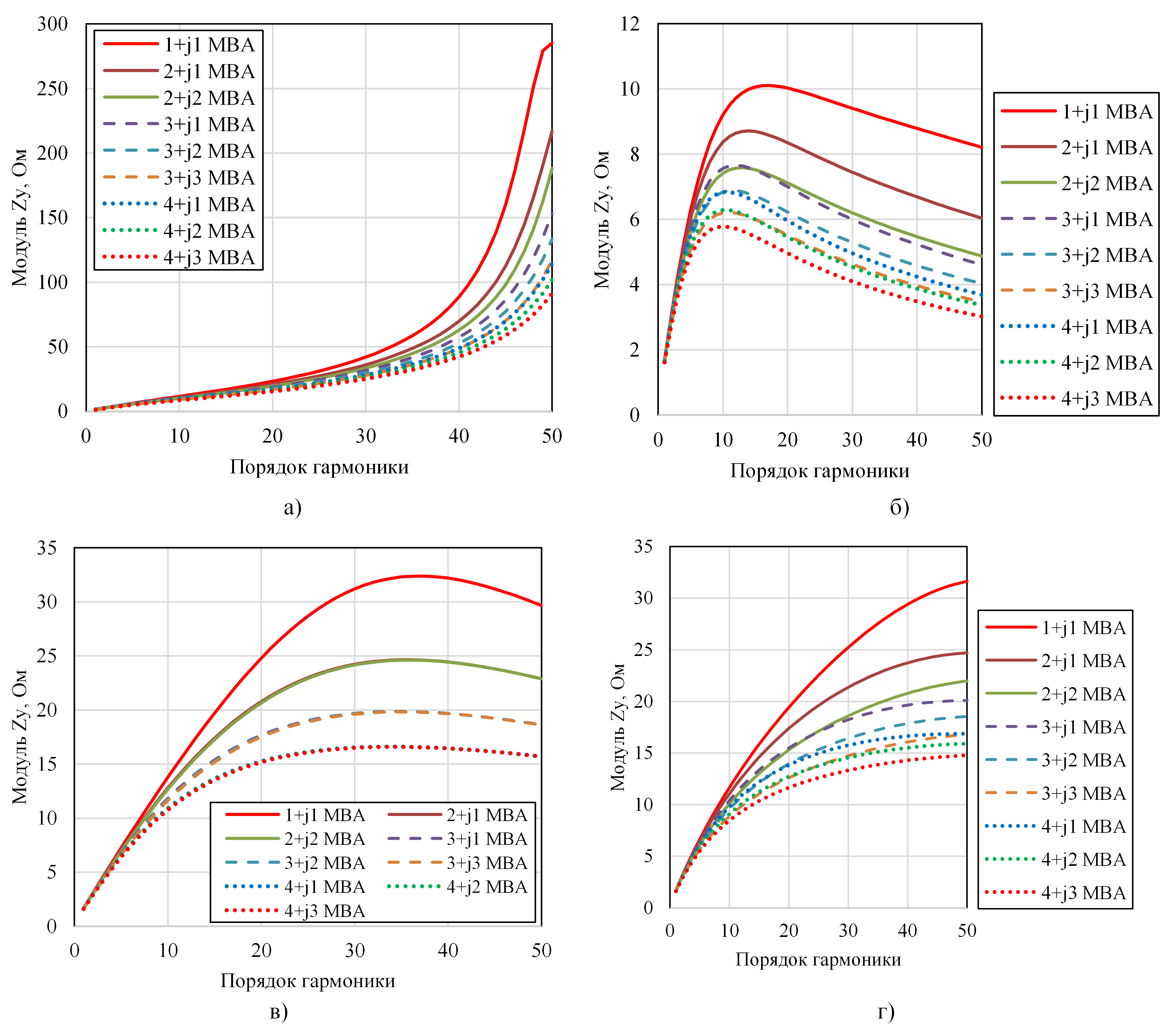
Рисунок 5 - АЧХ для узла 4 при изменении мощности нагрузки:
а - для модели 1; б - для модели 2; в - для модели 3; г - для модели 4
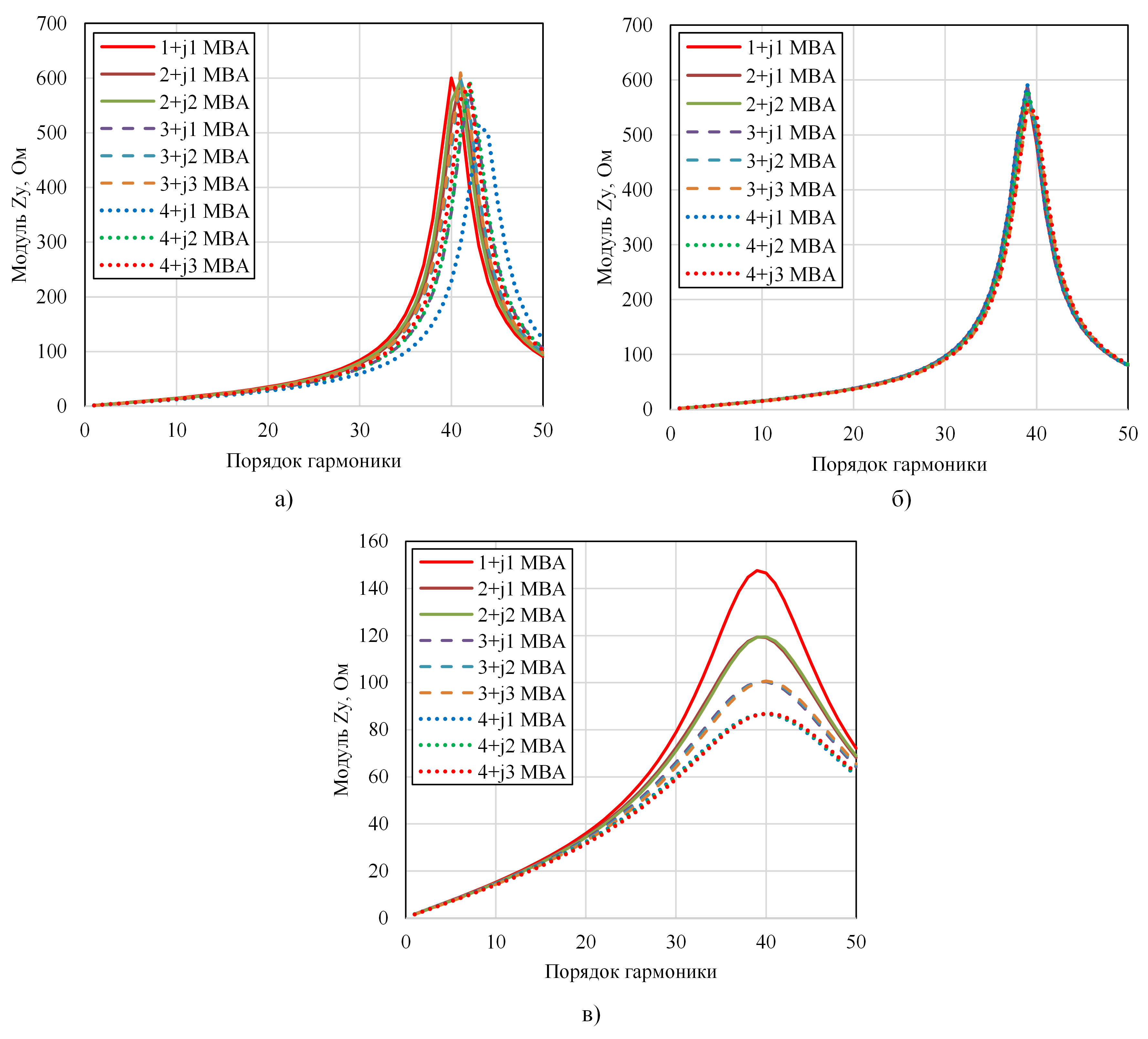
Рисунок 6 - АЧХ для узла 4 при изменении мощности нагрузки:
а - для модели 5; б - для модели 6; в - для модели 7
Модель 2: имеется максимум характеристики, однако он не характеризует параллельный резонанс, так как фазочастотная характеристика (не показанная здесь для упрощения) не проходит в данном случае через ноль. Абсолютные величины узлового сопротивления, как и ранее, существенно меньше по величине, чем у других моделей.
Модель 3: также есть слабовыраженный максимум и, как и в предыдущем случае, не связанный с параллельным резонансом. Для этой модели наблюдается группировка зависимостей по активной мощности: изменение реактивной мощности в широких пределах (например, от 1 до 3 Мвар) при одной и той же активной мощности практически не влияет на форму и амплитуду характеристики.
Модель 4: монотонное уменьшение амплитуды с увеличением мощности нагрузки, резонансные явления до 2500 Гц отсутствуют. Абсолютные величины характеристик Zу близки к таковым для модели 3, но здесь имеется выраженная зависимость от величины реактивной мощности.
Модель 5: изменение характеристики в функции мощности (как активной, так и реактивной) слабо выражено в области до 3+j3 МВА, далее отношение P/Q оказывает большее влияние. Во всех случаях наблюдается параллельный резонанс, при увеличении мощности от 1+j1 МВА до 4+j3 МВА резонансная частота изменяется на 159 Гц.
Модель 6: характеристика практически одинакова для всех мощностей. При увеличении мощности от 1+j1 МВА до 4+j3 МВА амплитуда характеристики на частоте резонанса изменяется всего на 4,97%, а сама резонансная частота — на 23Гц.
Модель 7: как и для модели 3, наблюдается группировка зависимостей по активной мощности. Во всех случаях имеется параллельный резонанс, его частота при увеличении мощности от 1+j1 МВА до 4+j3 МВА изменяется всего на 51 Гц.
Если в сети среднего напряжения есть батареи конденсаторов для компенсации реактивной мощности, то их влияние на частотные характеристики узлов сети, как правило, оказывается решающим. Включение батареи конденсаторов практически всегда приводит к появлению параллельных (а иногда и последовательных) резонансов в диапазоне частот до 2500 Гц. Для данной модельной схемы был проведен расчет частотных характеристик при мощности нагрузки S3, равной 2+j1 МВА, и включении конденсаторной батареи CB на ее шинах с мощностью 500 квар, а затем 1000 квар. Результаты расчета резонансных частот (для параллельных резонансов) и соответствующих максимумов АЧХ приведены в табл. 1. и табл. 2 соответственно.
Таблица 1 - Резонансные частоты узлов нагрузки при наличии батареи конденсаторов
Узел | Резонансная частота, Гц, для модели нагрузки | ||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | |
Мощность батареи 500 квар | |||||||
2 | 662 | - | 528 | 592 | 584 | 557 | 554 |
3 | 682 | - | 555 | 623 | 588 | 560 | 565 |
4 | 698 | 799 | 584 | 662 | 590 | 562 | 572 |
Мощность батареи 1000 квар | |||||||
2 | 451 | - | 385 | 417 | 418 | 399 | 397 |
3 | 466 | 520 | 401 | 435 | 421 | 402 | 405 |
4 | 479 | 477 | 416 | 454 | 424 | 404 | 411 |
Таблица 2 - Резонансные максимумы АЧХ узлов нагрузки при наличии батареи конденсаторов
Узел | Резонансный максимум АЧХ, Ом, для модели нагрузки | ||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | |
Мощность батареи 500 квар | |||||||
2 | 14,37 | - | 9,73 | 9,72 | 33,29 | 35,29 | 19,15 |
3 | 24,53 | - | 14,99 | 15,22 | 56,41 | 59,04 | 31,49 |
4 | 39,88 | - | 22,33 | 23,68 | 85,99 | 88,48 | 47,28 |
Мощность батареи 1000 квар | |||||||
2 | 9,93 | - | 8,17 | 8,19 | 19,73 | 21,28 | 13,37 |
3 | 16,63 | 7,89 | 12,86 | 13,09 | 33,48 | 35,68 | 22,05 |
4 | 26,75 | 13,43 | 19,39 | 20,37 | 51,62 | 54,05 | 33,45 |
На этом этапе исследования, помимо параллельных, в узлах 2 и 3 зафиксированы также и последовательные резонансы, характеризуемые локальным минимумом АЧХ. При мощности батареи 500 квар для узла 2 они находились в диапазоне от 17-й до 22-й гармоники (в зависимости от принятой модели нагрузки), для узла 3 – в диапазоне от 23-й до 29-й гармоники; при мощности батареи 1000 квар диапазоны составили от 13-й до 16-й и от 17-й до 21-й гармоники соответственно.
Как видно из табл. 1, резонансные частоты для моделей 5, 6 и 7 и в этом случае практически совпадают, различие между ними не превышает 5,3%. Характеристики для модели 2, как и ранее, сильно отличаются по форме и амплитуде от характеристик других моделей; резонанс имеется не всегда, и в том случае, когда он присутствует, частота значительно отличается от резонансных частот характеристик других моделей.
Из таблицы 2 следует, что для моделей 5 и 6 величины резонансных максимумов, как и резонансные частоты, практически совпадают: различие не превышает 7,3%. Однако для модели 7 характеристика проходит существенно ниже, и ее максимум почти вдвое меньше, чем для моделей 5 и 6. Характеристики моделей 3 и 4 близки по амплитуде (различие не более 5,7%), но имеют существенно разные резонансные частоты, как можно видеть из таблицы 1. Характеристики моделей 1 и 2, в свою очередь, сильно отличаются от предыдущих как по величине узлового сопротивления, так и по резонансным частотам.
Проведенные расчеты для условия включения батареи конденсаторов различной мощности в других узлах нагрузки (узлы 2 и 3 на рис. 2) привели к качественно таким же результатам.
4. Заключение
Наиболее общий вывод данного исследования состоит в том, что частотные характеристики узловых сопротивлений при разных моделях нагрузки существенно различаются между собой как по амплитуде, так и по резонансным частотам. Это не согласуется с выводами, приведенными в , и частично согласуется с данными, приведенными в . В указано, что при разных моделях нагрузки величины узловых сопротивлений различаются, а резонансные частоты практически одинаковы; между тем приведенные здесь результаты показывают, что и резонансные частоты также существенно различны. Предположительно, это может быть объяснено уменьшением вклада нагрузки в частотные характеристики узлов по мере увеличения размера сети и удельного соотношения сопротивлений нагрузки и других элементов (линии электропередачи, трансформаторы и др.). Следовательно, необходимо дальнейшее исследование этого вопроса на примере более крупных модельных сетей.
Изменение частотных характеристик при увеличении мощности нагрузки, а также при изменении соотношения P/Q также неодинаково для разных моделей нагрузки. Для моделей 3 и 7 изменение соотношения P/Q практически не влияет на АЧХ. Для модели 6 характеристика практически не изменяется как при увеличении мощности нагрузки, так и при изменении соотношения P/Q; несколько большее влияние указанные факторы оказывают на характеристики для модели 5.
Для моделей 5, 6 и 7 резонансные частоты (а для моделей 5 и 6 – также и амплитуды) оказались практически одинаковыми во всех вариантах расчетов. Поэтому при исследовании электрических сетей на предмет появления резонансов можно использовать любую из них. Другие модели нагрузки дают существенно отличные результаты. В особенности это характерно для модели 2, что объяснимо уменьшением ее активного и индуктивного сопротивления с ростом частоты, в то время как параметры других моделей либо принимаются неизменными, либо характеризуются возрастающими функциями от частоты. Учитывая, что расчетные выражения модели 2 не имеют обоснования и не согласуются с физикой процессов на высших частотах, ее применение не рекомендуется. В целом следует заключить, что выбор той или иной модели нагрузки для проведения исследований электрической сети в области частот высших гармоник (например, поиск резонансных частот) окажет значительное влияние на получаемые результаты.
Поскольку для различных моделей нагрузки частотные характеристики получаются существенно различными, возникает вопрос о том, какая модель наиболее адекватно описывает частотные свойства линейной нагрузки. Представляется необходимым проведение экспериментальных исследований в данной области и сопоставление полученных данных с приведенными здесь результатами.
