Оценка отличия прогнозов по модели на основе усреднённых экспериментальных данных от возможных отклонений протекания процесса под действием случайных факторов (на примере процесса биоразложения парацетамола)
Оценка отличия прогнозов по модели на основе усреднённых экспериментальных данных от возможных отклонений протекания процесса под действием случайных факторов (на примере процесса биоразложения парацетамола)
Аннотация
В работе рассматривается влияние случайного фактора на результаты экспериментальных измерений и, как следствие, на решение оптимизационной задачи идентификации параметров математической модели и результаты прогнозирования на примере процесса разложения парацетамола штаммом бактерий Staphylococcus sciuri DPP1. Предлагается подход к решению обозначенной проблемы на основе ряда вычислительных экспериментов с внесением искусственных погрешностей в усредненные экспериментальные данные процесса в рамках доверительного интервала случайным образом или в виде системных отклонений к его границам. Вычислительные эксперименты проводились с помощью специально разработанного программного модуля на языке C#. Отличия результатов решения оптимизационной задачи оценивались как непосредственно в единицах определяемых параметров, так и на основе выходных характеристик модели, таких как дисперсия адекватности, наибольшее отклонение относительной погрешности при сравнении кинетических кривых, общее время протекания процесса. Также дана сравнительная оценка влияния концентрации парацетамола на возможные отклонения длительности его разложения, что необходимо учитывать при проектировании технологии.
1. Введение
Известно, что при проведении повторных экспериментальных измерений каждая новая реализация процесса при одинаковых условиях отличается от предыдущей, то есть получение идеально повторяющихся результатов почти невозможно. На протекание любого процесса оказывают влияние различные случайные факторы, имеющие как внутреннюю, так и внешнюю природу . К примеру, на процессы биодеструкции сложных органических соединений оказывают влияние такие факторы, как наличие в средах обитания микроорганизмов посторонних веществ, способных являться модификаторами роста клеточных популяций, накопление продуктов метаболического разложения сложных субстратов, температура, кислотность, пространственное распределение клеточной популяции в среде обитания, как внешние факторы, а также различные отклонения метаболической активности отдельных представителей популяции, как внутренний фактор. При этом стоит отметить, что все методики оценки количества клеток достаточно приближённые, поэтому воспроизводимость любых биопроцессов зачастую отличается крайне низкими характеристиками . При дальнейшем представлении полученных данных каждый экспериментальный результат — есть следствие статистической обработки повторных измерений, чаще всего выраженной в их усреднении . Так, для оценки повторяемости измерений рассчитывается дисперсия воспроизводимости для процесса в целом и доверительные интервалы для отдельных экспериментальных точек. Однако, как правило, для оценки параметров математических моделей используются только усреднённые замеры, исключающие влияние случайного фактора на протекание процесса. То есть, построенная математическая модель способна описывать только основные усреднённые характеристики и, как следствие, давать такие же усреднённые прогнозы. Оценка отличий таких прогнозов от возможных отклонений протекания процесса под действием случайного фактора, как правило, не проводится. Однако в отдельных случаях, особенно для процессов с низкой воспроизводимостью, может быть актуальна задача получения такой оценки для определяющих характеристик процесса, которые необходимо учитывать при разработке технологических регламентов.
Сама постановка задачи влияния случайных факторов на результат решения задачи идентификации параметров математических моделей и, как следствие, на результаты прогнозирования по модели и её решение в настоящее время становится реалистичным с учётом постоянно развивающихся возможностей компьютерных и вычислительных технологий. В прежние поколения вычислительных систем решение подобных задач было крайне затруднительно из-за недостаточных компьютерных мощностей, поэтому такие исследовательские задачи в принципе не ставились. Изучение технологических процессов и соответствующее им моделирование проводилось в устойчивых областях, где достоверность результатов прогнозирования можно было обосновать теоретически. Однако, развитие научных представлений о системах со сложным динамическим поведением, спонтанных сменах их режимов поведения, теории бифуркаций и катастроф и т.п. способствовало возникновению предпосылок для анализа влияния случайного фактора на протекание процессов и на числовые характеристики экспериментальных измерений, на значения параметров моделей сложных систем, идентифицируемых по этим измерениям, и, как следствие, на прогностические свойства этих моделей , . Причём наибольшую значимость данные исследования будут иметь в таких областях, как биотехнология, метеорология, медицина и т.д., где в силу сложности самих систем вариабельность протекания процессов достаточно высока.
В научной периодике можно встретить анализ влияния случайного фактора на скорость процесса биодеструкции лекарственного препарата в качестве нестационарного случайного процесса, описанного обычной функцией системы двух случайных величин с применением кинетического моделирования реализаций процесса . В работе было отмечено, что математическое моделирование процесса без углубленного анализа экспериментальных данных биопроцессов и влияния случайного фактора на его скорость, в том числе применение пакетов программ для стохастического анализа, может привести к некорректным результатам. Использование современного подхода к моделированию биотехнологических процессов — нейронных сетей, — позволяет строить закономерности на основе необходимого количества выборок экспериментальных данных . При этом нейронные сети косвенно учитывают случайный фактор, поскольку любая выборка сама по себе является случайным результатом. Однако при этом такой подход не позволяет отделить отдельные случайные влияния от основных закономерностей протекания процесса, и, более того, не позволяет их обосновать с физической точки зрения. Поэтому именно для оценки влияния случайного фактора нейронные сети неперспективны.
В настоящей работе подобный анализ предлагается для конкретного процесса биоразложения парацетамола штаммом бактерий Staphylococcus sciuri DPP1. Микроорганизмы рода Staphylococcus способны разрушать парацетамол, используя входящий в него углерод в качестве единственного источника углерода и энергии. Экспериментальные изменения концентрации парацетамола при разных условиях описаны в . В представлен анализ этих экспериментальных данных, обоснованы положения математической модели процесса, описаны используемые уравнения и найдено частное решение оптимизационной задачи идентификации параметров модели. В работе были выявлены корреляции между искомыми параметрами модели, введение которых в оптимизационную задачу позволяет понизить порядок её размерности и обосновать многовариантность её решения наличием овражной функции на поверхности отклика. В настоящем исследовании предлагается подход к решению обозначенной проблемы на основе ряда вычислительных исследований на базе уже построенной математической модели, отражающей природу процесса, с найденными параметрами модели и взаимосвязями между ними , и продемонстрирован результат, показывающий насколько случайный фактор экспериментальных измерений оказывает влияние на прогноз по модели.
2. Краткое описание математической модели процесса биоразложения парацетамола и результатов оценки её параметров
Математическое описание процесса биодеструкции парацетамола, учитывающее протекание процесса биоразложения через образование промежуточного метаболита (z), ингибирующего процесс в целом (кинетическая схема представлена на рис. 1) , включает классические для биотехнологии дифференциальные уравнения изменения концентраций субстрата, z-метаболита и биомассы, а также уравнение Моно, модифицированное с учётом ингибирования начальной стадии разложения z-метаболитом и уравнение Моно без учёта какого-либо ингибирования для описания удельной скорости последующего распада z-метаболита . В результате проведённых ранее исследований были найдены зависимости максимальных удельных скоростей стадий процесса от начальной концентрации субстрата в среде и корреляции между параметрами этих зависимостей :
где k11, k12, k13 — параметры уравнения зависимости максимальной удельной скорости начальной стадии процесса от исходной концентрации парацетамола в среде; k22, k23 — аналогичные параметры для стадии распада z-метаболита.
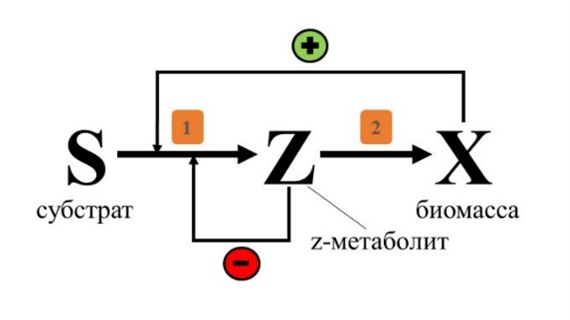
Рисунок 1 - Ингибирование распада парацетамола промежуточным z-метаболитом
В результате решения оптимизационной задачи (2) методом сканирования была исследована поверхность отклика и определён глобальный экстремум, соответствующий значениям: k11 = 0,315, k22 = 0,111.
3. Постановка задачи исследования и используемые методы
Задача исследования влияния случайных факторов при протекании процесса на прогнозирование по модели предполагает проведение серии вычислительных экспериментов с учётом внесения случайных искусственных помех в усреднённые экспериментальные данные в рамках их доверительных интервалов согласно реально полученным измерениям . То есть, предполагается, что траектория процесса не обязательно должна соответствовать усреднённым значениям измерений в каждой временной точке, а может пойти по любому сценарию в допустимом диапазоне.
Для проведения вычислительных экспериментов был разработан программный модуль на языке C# — WPF-приложение «Программа для исследования влияния случайного фактора погрешности экспериментальных измерений на идентификацию параметров математической модели процесса биоразложения парацетамола», в которой реализован поиск оптимальных значений параметров модели методом сканирования в зависимости от внесённых пользователем погрешностей в экспериментальные данные.
Программный комплекс состоит из нескольких логически связанных модулей:
– основной блок, в котором задаются взаимосвязи между другими блоками, запись введенных пользователем технических характеристик процесса, алгоритм действий при выборе размерности оптимизационной задачи, вывод данных и запись их в Excel-файл;
– блок задания экспериментальных данных, включающий непосредственно усреднённые измерения из , данные по границам доверительных интервалов отдельных экспериментальных точек, а также алгоритм случайного либо закономерного (по выбору пользователя) разброса погрешностей относительно усреднённых значений;
– блок расчёта математической модели процесса биоразложения парацетамола согласно описанию из либо (по выбору пользователя) той же модели, но с учетом найденных взаимосвязей параметров (1);
– блок реализации оптимизационного алгоритма методом покоординатного спуска либо методом сканирования в зависимости от выбранной ранее размерности оптимизационной задачи.
Разработанное приложение позволяет провести моделирование процесса и определить константы как пятимерной оптимизационной задачи, так и двумерной с учётом соотношений (1). При этом пользователю предлагается выбор исходной экспериментальной информации о процессе: усредненные значения, принимаемые за «эталон», или один из вариантов имитации погрешностей в этих значениях. Может быть задана системная погрешность в виде отклонений в сторону верхней либо нижней границы доверительного интервала, или же хаотичная погрешность в рамках доверительного интервала. В качестве выходных данных работы программы в отдельный Excel-файл выводится поверхность отклика (2) (в случае решения двумерной оптимизационной задачи), а также информация о погрешностях в данном вычислительном эксперименте.
4. Исследование зависимости влияния случайных факторов при протекании процесса биоразложения парацетамола на прогнозирование по модели
С целью исследования влияния случайных факторов, определяющих результат отдельных замеров по ходу процесса, на решение оптимизационной задачи (2) и важные технические характеристики процесса, проводилась серия вычислительных экспериментов, результаты которых представлены на рис. 2. В ходе вычислительного эксперимента в экспериментальные данные из , принятые за «эталон», случайным образом вносилась погрешность одним из четырёх способов:
1) случайное распределение по экспериментальным точкам одинаковой по абсолютной величине, но разной по знаку погрешности, сопоставимой с точностью экспериментальных измерений, т.е. 10-2 (ВЭ-1);
2) случайное распределение по экспериментальным точкам погрешности с переменной абсолютной величиной в области доверительного интервала (ВЭ-2);
3) системное отклонение от «эталонных» значений в сторону верхней границы доверительного интервала с переменной абсолютной величиной (ВЭ-3);
4) системное отклонение от «эталонных» значений в сторону нижней границы доверительного интервала с переменной абсолютной величиной (ВЭ-4).
При этом дополнительно исследовались сами границы доверительного интервала как отдельные вычислительные эксперименты: по верхней границе доверительного интервала (ВГ) и по нижней (НГ).
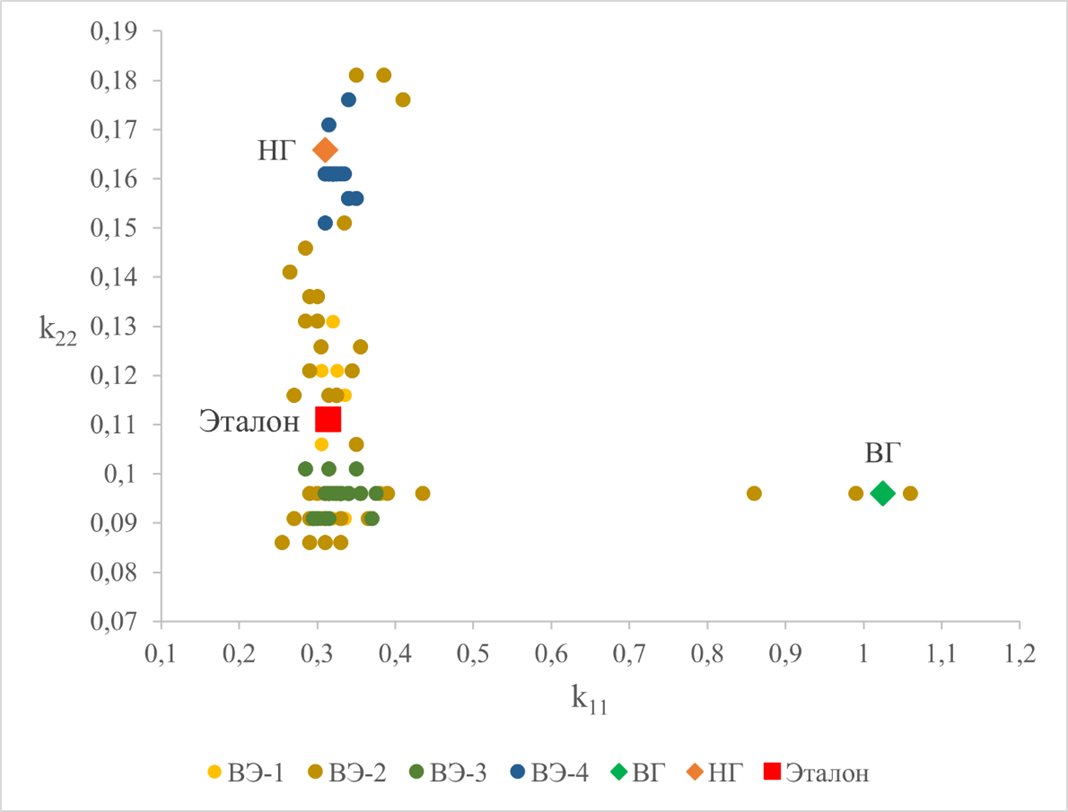
Рисунок 2 - Разброс оптимумов, полученных в ходе проведения вычислительных экспериментов
Примечание: описание обозначений приведено в тексте работы
Таким образом, ещё раз подчеркнём, что в области решений, близких к нижней границе доверительного интервала выше чувствительность решения оптимизационной задачи к значению параметра k22, а для верхней границы — к значению параметра k11. Для случайных распределений в окрестности усреднённых исходных данных («эталонного» решения) чувствительность к обоим параметрам становится сопоставимой, чем, видимо, и объясняется, что «эталонное» решение расположено в стороне от прямой, соединяющей «пограничные» решения. Обнаруженные закономерности в найденных решениях оптимизационной задачи в рамках рассматриваемой математической модели процесса говорят о том, что введение системных погрешностей в сторону верхней границы доверительного интервала увеличивает влияние первой стадии процесса, непосредственно разложения парацетамола, а в сторону нижней границы – влияние второй стадии процесса, разложение промежуточного метаболита-ингибитора.
5. Оценка влияния многовариантности решения оптимизационной задачи на прогнозирование по модели
На следующем этапе предстояло выяснить, насколько отдельные частные решения оптимизационной задачи (2), зависящие от случайного фактора результатов экспериментальных измерений, влияют на прогнозирование по модели. Значимость такого исследования заключается в оценке влияния исходных данных на погрешность результатов прогнозирования характеризующих протекание процесса параметров, поскольку, как правило, при исследовании процессов методами математического моделирования описываемые в настоящей работе комплексные исследования не проводятся и в качестве итогового результата получается единственное решение, которое, как было показано выше, носит в какой-то степени усреднённый, а в какой-то степени случайный характер. Иначе говоря, проведённые исследования позволяют оценить отличие временных диапазонов биоразложения парацетамола, которые могли бы быть получены, когда «единственным» решением оптимизационной задачи (2) могло оказаться любое из представленных на рис. 2.
В качестве отправной точки для сравнения результатов был принят оптимум из работы , названный выше «эталоном». Критериями оценки были приняты показатели, также описанные в работе : дисперсия адекватности, наибольшее отклонение относительной погрешности при сравнении кинетических кривых, общее время протекания процесса.
Как показали результаты вычислительных экспериментов, отклонение по дисперсии адекватности может достигать 55% при среднем значении данного показателя — 16%. Отклонение кинетических кривых, численно выраженное относительной погрешностью, составило не более 15% при среднем значении 8%. На рис. 3 представлены кинетические кривые для четырёх вычислительных экспериментов — «эталона» (k11 = 0,315, k22 = 0,111), по верхней (k11 = 0,31, k22 = 0,166) и нижней (k11 = 1,025, k22 = 0,096) границам доверительного интервала, а также произвольно выбранный вычислительный эксперимент (k11 = 0,335, k22 = 0,091). Видно, что кинетические кривые для случайного решения визуально практически полностью накладываются на «эталон», что говорит о том, что представленные выше средние значения оцениваемых показателей небольшие и влияние случайного фактора на протекание процесса в целом незначительно. Однако на границах доверительного интервала наблюдаются заметные отклонения в кинетике особенно для низких концентраций парацетамола.
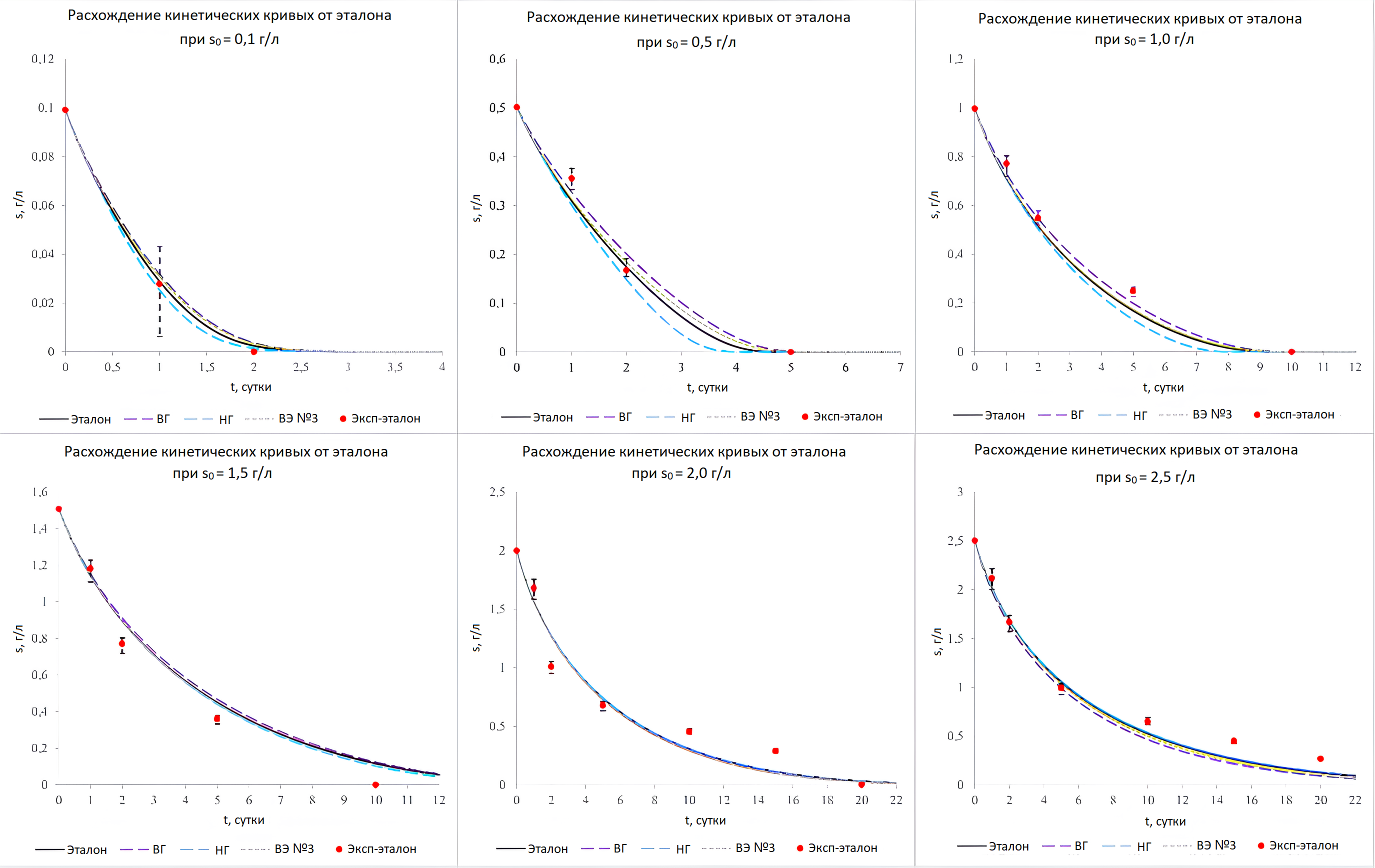
Рисунок 3 - Отклонение кинетических кривых решения вычислительных экспериментов от «эталона»:
длинным штрихом отображены кривые, соответствующие решениям по верхней (ВГ) и нижней (НГ) границе доверительного интервала; короткий штрих – решение произвольного вычислительного эксперимента (ВЭ №3); сплошной линией – «эталон»
Также определены различия по третьему показателю (времени протекания процесса) для разных значений исходной концентрации парацетамола в среде: при малой концентрации субстрата (0,1 г/л) наблюдаются отклонения времени процесса не более 4 часов (в 7,5% относительно «эталона»); с увеличением исходной концентрации до 0,5 г/л наблюдается ускорение или замедление процесса от усредненного результата до 16 часов (в 14,9% относительно «эталона»); при 1,0 г/л и выше данный показатель достигает 43 часов (в 14,5% относительно «эталона»), что следует учитывать при прогнозировании процесса и проектировании его в промышленных масштабах.
6. Заключение
Таким образом, проведённые исследования показывают, что усреднение экспериментальных данных и пренебрежение случайными факторами приводит к частичной потере информации о протекании процесса. Это может численно выражаться в отклонениях значимых характеристик и параметров процесса от предсказания по модели, что необходимо учитывать при проектировании этих процессов. При этом современные вычислительные технологии вполне позволяют дать оценку таким отличиям при грамотной постановке задачи исследования.
