Модельное исследование чувствительности глобального климата к изменениям солнечного излучения

Климатическая система включает атмосферу, океан (с морским льдом) и деятельный слой суши (почва и растительность) как взаимодействующие между собой блоки

Существует спектр моделей климата, от простейших точечных, предельно осреднённых, до сложнейших трехмерных, с развитыми блоками радиации, океана и атмосферы

Параметризацию гидродинамических процессов естественно реализовывать путём термодинамического описания системы в целом. Адем

При понижении приземной температуры увеличивается доля площади Земли, покрытой снегом и льдом, увеличивается количество отраженной в космос радиации (увеличивается альбедо земной поверхности и системы в целом) и температура еще более понижается. Эта альбедо-температурная обратная связь – положительная, она усиливает воздействие первоначальной причины.

Климатическая система представлена в виде двух блоков: блок атмосферы и блок деятельного слоя (океан или почва – в зависимости от локализации блока). В предположении, что теплоёмкость атмосферы мала по сравнению с теплоёмкостью деятельного слоя, уравнение энергетического баланса климатической системы можно записать в виде

где T – температура приземного слоя атмосферы, c – теплоемкость деятельного слоя, t – время, s – поток солнечной энергии на верхней границе атмосферы,  – альбедо климатической системы, I – длинноволновое (тепловое) излучение в пространство, F – параметр, описывающий горизонтальный меридиональный суммарный турбулентный перенос тепла. В качестве независимой переменной использована величина , где  – географическая широта.

Гидродинамические потоки тепла F, в предположении макротурбулентной теплопроводности по типу законов Фурье, пропорциональны градиенту температуры , где D0 – коэффициент макротурбулентной теплопередачи или диффузии. Количество тепла, покидающее единичную площадку данной широтной полосы за единицу времени, есть дивергенция указанной величины:

Окончательно получим следующую систему:

Второе уравнение определяет отсутствие горизонтального макротурбулентного потока тепла в граничных точках x1 и x2 (южный и северный полюса, соответственно). Эти условия необходимы при использовании сферической системы координат, в которой на полюсах существуют особые точки, где пересекаются меридианы. Поток солнечной энергии на верхней границе атмосферы представлен произведением солнечной постоянной Q на заданную функцию S(x,t), определяющую распределение этого потока на Земле в зависимости от широты и времени года

Важной особенностью модели является наличие зависимости коэффициента поглощения от температуры. Предполагается, что в тех областях, где температура атмосферы становится ниже -10оС, присутствует устойчивый снежный покров и коэффициент поглощения резко понижается до постоянной величины a=0,395 

Первый численный эксперимент в рамках модели был проведен для определения выхода на установившийся климат в условиях сезонного хода солнечной радиации. В качестве начальных условий использована постоянная нулевая температура атмосферы. Примерно через 4 расчетных года достигается стационарное состояние с меняющейся в соответствии с сезоном температурой и положением снеговой линии. Изменение среднеглобальной температуры атмосферы представлено на рис. 1а. На рис. 1б показаны сезонные изменения положения снеговой линии для северного полушария. В летний сезон снег полностью тает (), а в зимний граница расположена примерно на широте 60о. Период колебаний на рис.1 равен 1 году. Расчеты здесь и далее проведены для значения теплоемкости, соответствующей толщине деятельного слоя примерно 10 м

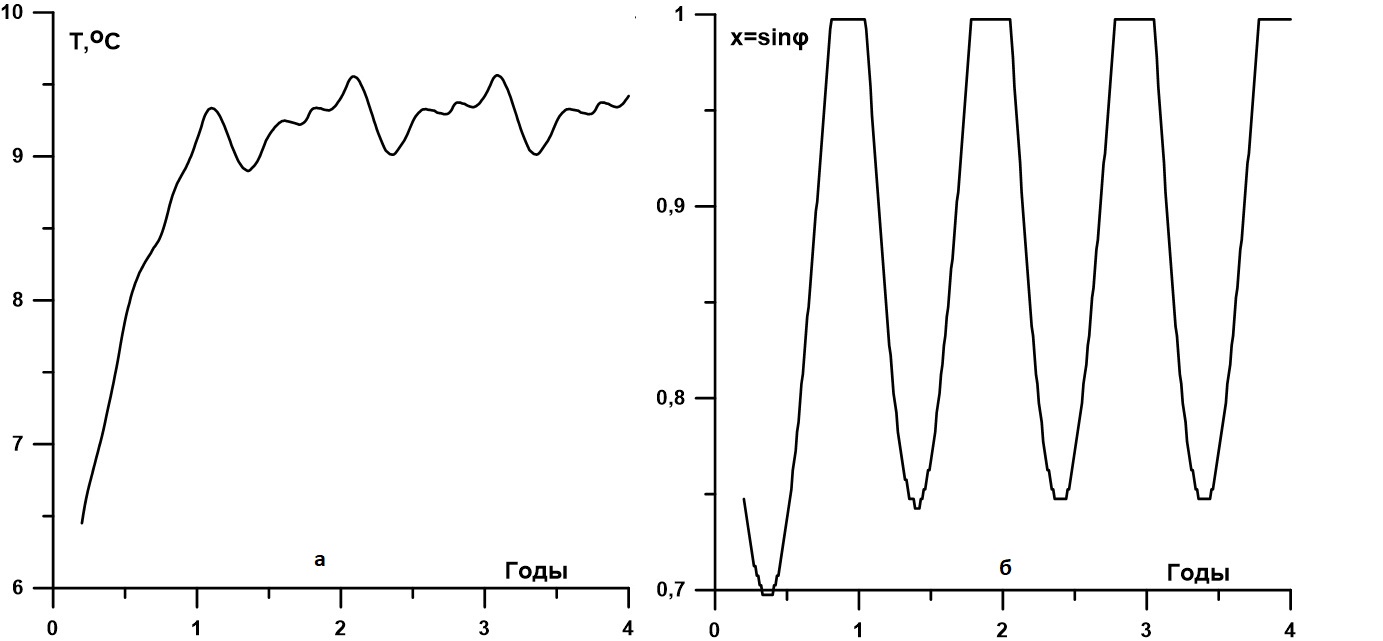
Рисунок 1 - Выход на установившийся сезонный режим климата:

а - средне глобальная приземная температура атмосферы; б - положение снеговой линии

DOI:10.23670/IRJ.2023.128.90.2

В дальнейших расчетах исследуется влияние на модельный климат изменения солнечной постоянной Q. Расчеты ведутся с начальных условий, соответствующих установившемуся климатическому состоянию. На этапе 1 (рис. 2) происходит плавное уменьшение относительного значения солнечной постоянной (красные линия и шкала) во времени и координата снеговой линии (чёрная линия) в зимний период постепенно смещается к экватору. Для каждого фиксированного значения Q расчет ведется в течение 2-х лет. Колебания снеговой линии имеют период 1 год и соответствуют сезонным изменениям. При дальнейшем уменьшении Q снег даже в летний период присутствует в приполярных областях. При Q= 0,96 происходит лавинообразное смещение снеговой линии до экватора, и Земля полностью покрывается снегом и льдом (режим оледенения). При дальнейшем уменьшении Q температуры просто понижаются. На этапе 2 расчетов происходит постепенное увеличение Q, климат постепенно теплеет, но Земля по-прежнему полностью покрыта снегом и льдом и при Q=1. Всё начинает стремительно таять только при увеличении Q до значения 1,42 и Земля полностью освобождается от снега и льда, устанавливается бесснежный теплый период. Далее, на этапе 3, моделируем уменьшение Q, при этом постепенно появляются снежные области в зимние периоды и при Q=1 климат возвращается к исходному. Аналогичные результаты и выводы относятся и к южному полушарию (рис. 2). Всего расчеты проведены на период около 400 лет, на рис. 2 некоторые неинформативные промежутки времени опущены.

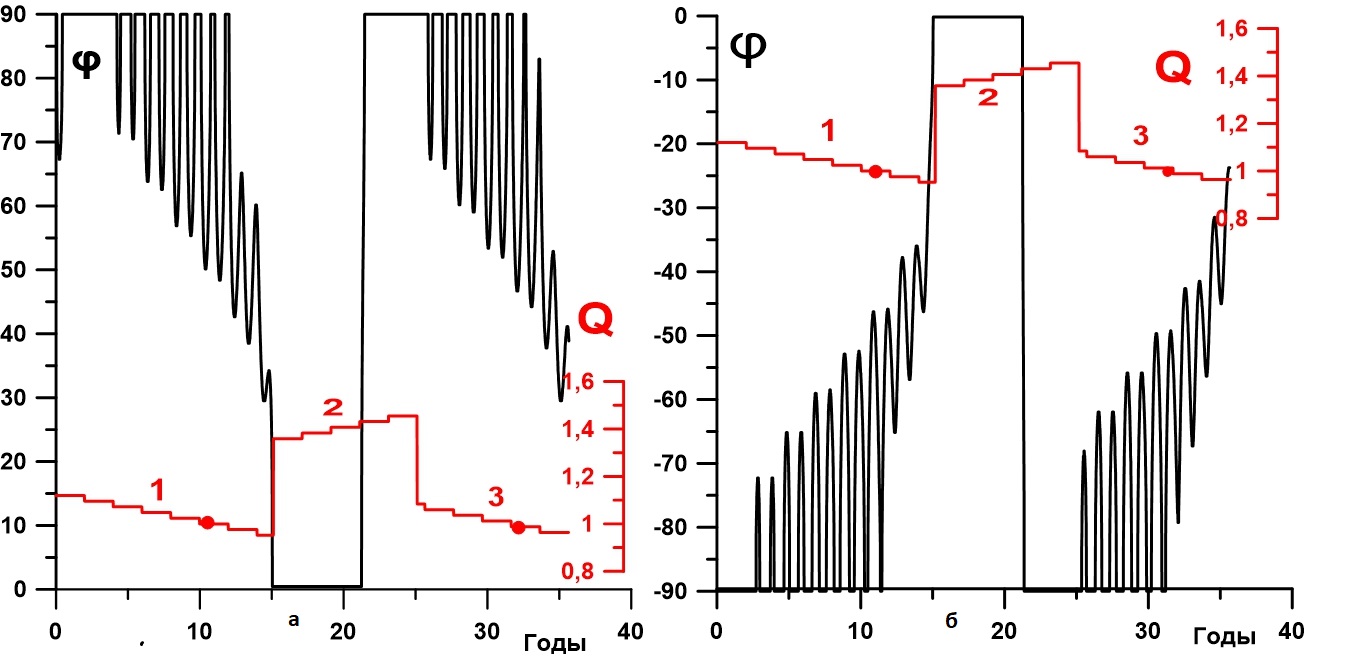
Рисунок 2 - Эволюция положения снеговой линии (чёрная линия) при изменении солнечной постоянной (красная линия):

а - Северное полушарие; б - Южное полушарие

DOI:10.23670/IRJ.2023.128.90.3

На рис. 3 приведены изменения во времени средне глобальных значений температуры при описанных выше изменениях Q. Отметим резкое понижение температуры при наступлении оледенения (период 1) и необходимое значительное её повышение в периоде 2 для начала таяния снега и льда и прекращения оледенения.

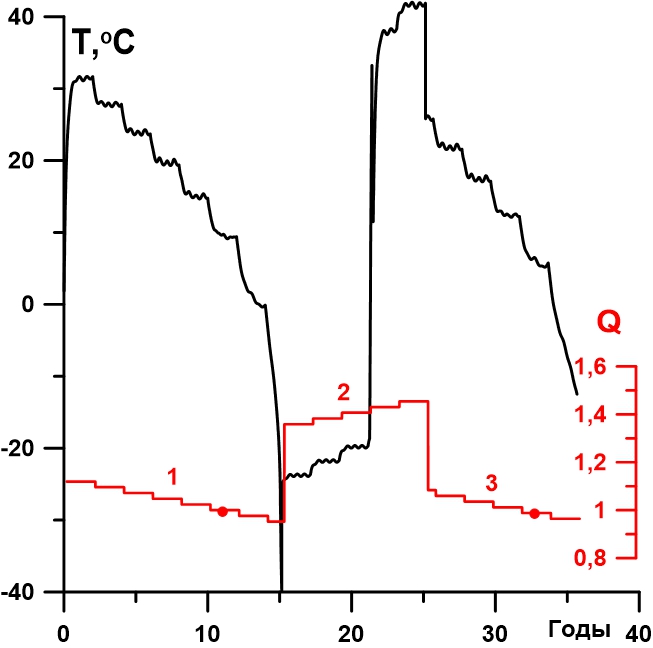
Рисунок 3 - Эволюция средне глобальной приземной температуры атмосферы (чёрная линия) при изменении солнечной постоянной (красная линия)

DOI:10.23670/IRJ.2023.128.90.4

По сравнению с классическим построением энергобалансовых моделей здесь введена эволюция во времени и совместное рассмотрение северного и южного полушарий, имеющих свои специфические характеристики, в частности зависящий от широты коэффициент поглощения солнечной радиации, задаваемый из данных наблюдений. Расчеты проведены в режиме реального сезонного хода солнечной радиации. Исследуется влияние на модельный климат изменения солнечной постоянной. Подтвержден классический результат, что и в этой постановке при уменьшении солнечной постоянной на 4% происходит лавинообразное смещение снеговой линии до экватора, и Земля полностью покрывается снегом и льдом (режим оледенения). Выход из этого режима наступает только при её увеличении на 40,2% по сравнению с современным значением.