ОЦЕНКА ФРАКТАЛЬНЫХ СВОЙСТВ НАНОСТРУКТУР ПО МИКРОСКОПИЧЕСКИМ ИЗОБРАЖЕНИЯМ

Оценка фрактальных свойств наноструктур по микроскопическим изображениям

Научная статья

Полищук С.В.^{1, *}, Петров К.А.²

¹ ORCID: 0000-0003-1764-485X;

^{1, 2} Дальневосточный федеральный университет, Владивосток, Россия

* Корреспондирующий автор (polischuk.sv[at]dvfu.ru)

Аннотация

В работе исследован метод анализа фрактальных свойств изображений на основе их структурной функции. Предложено расширение данного метода с целью анализа локальных фрактальных признаков. Исследован метод синтеза изображений со свойствами спектрального самоподобия и предложен метод модификации изображений во фрактальные с самоподобной структурной функцией на основе вейвлет-преобразований. Разработано программное средство для фрактального анализа микроскопических изображений с использованием исследуемых методов. Показана эффективность исследуемых методов посредством их проверки на смоделированных фрактальных изображениях. Предложено применение разработанных инструментов фрактального анализа в области электронной и оптической микроскопии.

Ключевые слова: фрактальный анализ, структурная функция, показателя Херста, метод Пентланда.

Evaluating Fractal Properties of Nanostructures from Microscopic Images

Research article

Polishchuk S.V.^{1, *}, Petrov K.A.²

¹ORCID: 0000-0003-1764-485X;

^{1, 2} Far Eastern Federal University, Vladivostok, Russia

* Corresponding author (polischuk.sv[at]dvfu.ru)

Abstract

The article investigates a method for analyzing fractal properties of images based on their structural function and proposes an extension of this method in order to analyze local fractal features. The authors investigate a method for synthesizing images with spectral self-similarity properties and propose a method for modifying images into fractal ones with a self-similar structural function based on wavelet transformations. Also, the authors introduce a software tool for fractal analysis of microscopic images using the methods featured in the study. The effectiveness of these methods is shown by means of their verification on modeled fractal images. The study proposes the application of the developed fractal analysis tools in the field of electron and optical microscopy.

Keywords: fractal analysis, structural function, Hurst exponent, Pentland method. Введение

В общем случае фрактальные свойства случайных процессов связаны с инвариантностью (самоподобием) относительно масштабных преобразований, или самоаффинностью. В то же время единственным критерием самоподобия статистической характеристики является ее распределение по степенному закону [1]. Таким образом, задачи фрактального анализа изображений сводятся к поиску статистических характеристик, удовлетворяющих данному условию, разработке алгоритмов расчета этих характеристик и классификации изображений на основе полученных фрактальных признаков [2].

В работе рассматривается один из алгоритмов фрактального анализа, его программная реализация, а также расширение алгоритма для анализа фрактальных свойств изображения в локальных областях.

Метод оценки фрактальных свойств

Исследуемый метод использует в качестве фрактальной меры самоподобие структурной функции изображения. Оценку структурной функции изображения получают из соотношения [3]:

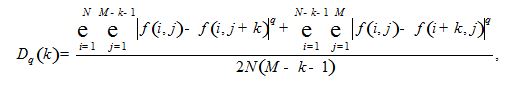(1)

где q – порядок структурной функции, f (i, j) – функция яркости изображения, N, M – число строк и столбцов матрицы изображения соответственно, k – размер измерительного окна (k<N, M). Как правило, программная реализация алгоритма использует структурную функцию первого порядка D₁(k), а коэффициент k подбирается эмпирически.

Если построенная таким образом оценка структурной функции изображения имеет степенной вид, значит, она обладает масштабной инвариантностью, т.е. фрактальными свойствами. В этом случае приближенное значение фрактальной размерности d можно получить из показателя Херста , который определяется как тангенс угла наклона прямой линейной регрессии для структурной функции [4]. Фрактальная размерность зависит от показателя Херста, как d = 3 - a.

Расширение метода для оценки локальных фрактальных свойств

Весьма часто на изображениях наноструктур присутствуют различные объекты, отличающиеся по своим статистическим характеристикам друг от друга, а также от фона. В этом случае оценка фрактальных свойств на всей матрице изображения может не дать желаемых результатов и имеет смысл провести дополнительный анализ, разбивая исходное изображение на фрагменты заданного размера [5].

Описанный выше алгоритм можно модифицировать с целью оценки локальных фрактальных свойств изображения [6]. Для этого перейдем от расчета показателя Херста на всем изображении к расчету локальных значений оценки этого показателя в скользящем окне размером NrM (на практике, как правило, скользящее окно квадратное, т.е. N=M). Структурная функция в данном случае так же рассчитывается из соотношения (1), но N и M означают размер скользящего окна.

В скользящем окне рассчитывается локальное значение оценки показателя Херста [7], для чего используются полученные значения структурной функции и ее аргумента k (размера измерительного окна):

Синтез изображений с фрактальными свойствами

Преобразование изображения во фрактальное производится в два этапа. На первом этапе происходит модификация спектра в степенную функцию, а на втором используется декомпозиция вейвлет-преобразованиями Гаусса и Морле, которые позволяют получить изображение со степенной структурной функцией.

Для преобразования цифрового изображения  f (j₁, j₂) в спектрально-самоподобное запишем его дискретное преобразование Фурье (ДПФ) как

спектр которого убывает по степенному закону. Данное изображение может принимать как положительные, так и отрицательные значения, поэтому, в случае необходимости, к нему добавляют постоянную составляющую для приведения к нормальному виду.

Формула (4) сохраняет информацию о фазе комплексных экспонент, на которые разлагается исходное изображение, но теряет информацию о локализации спектральных компонент и их квазипериодическом характере. Фрактальные свойства полученного изображения зависят от коэффициента b, задаваемого при моделировании степенной функции C(m, n).

Если построить структурные функции исходного изображения  f (j₁, j₂) и полученного спектрально-самоподобного  f₁ (j₁, j₂) в двойном логарифмическом масштабе (рисунки 1 (б) и 2 (а) соответственно),то можно видеть, что во втором случае функция более близка к степенной, однако наблюдается выраженное отклонение в области высоких частот. Это отклонение может присутствовать в разных областях и быть выражено в разной степени при работе с различными изображениями. Привести структурную функцию к степенному виду можно несколькими способами [8]. Один из них основан на декомпозиции изображения фильтрами вида H(u₁, u₂; m), где m – параметр, определяющий полосу пропускания фильтра (OJ mJ M-1 ) [9]. Для таких фильтров должно выполняться условие , а их сумма должна быть равна  (M – количество фильтров). При использовании таких фильтров равенство

          В результате декомпозиции получаем M изображений g(j₁, j₂;m), каждое их которых содержит информацию об определенном диапазоне частот исходного изображения (как правило, на практике для решаемых нами задач 2J M J 4). Те изображения, диапазон частот которых примерно соответствует области, на которой наблюдается отклонение в структурной функции исходного изображения, могут быть модифицированы простым домножением на числовой коэффициент, или, при необходимости, применением более сложной функции. 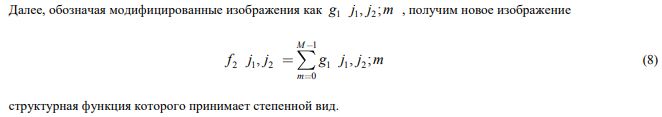Программная реализация и проверка методов

Было разработано программное средство, позволяющее производить оценку как глобальных, так и локальных фрактальных свойств растрового изображения. В первом случае результатом является график функции одной переменной D_q(k), для которого затем рассчитывается показатель Херста при помощи инструментов работы с графиками.Во втором случае результатом является двумерное поле распределения локальных значений оценки показателя Херста. Над этим полем можно проводить дополнительные операции, такие как построение гистограммы и сегментация для выделения участков с заданной фрактальной размерностью.

Кроме того, в рамках программного средства реализованы инструменты модификации изображения во фрактальное, как с самоподобным спектром, так и с самоподобной структурной функцией.

Для апробации предлагаемых в работе методов использовалось изображение аморфной пленки CoNiP, полученное на микроскопе CarlZeissLibra 200 FE при ускоряющем напряжении 200 кВ (рисунок 1 (а)).

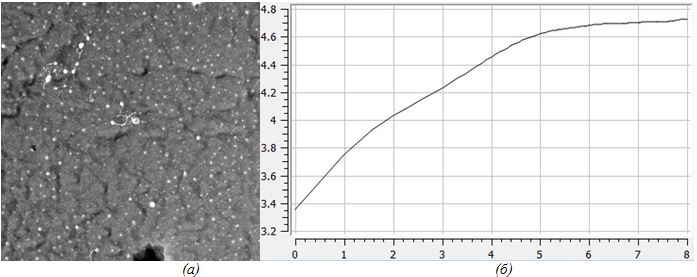
Рис. 1 – Изображение образца CoNiP(а) и его структурная функция 1-го порядка (б)

Для исследуемого изображения была построена структурная функция первого порядка (выражение 1) в двойном логарифмическом масштабе (рисунок 1 (б)). Можно видеть, что структурная функция не является степенной. Изображение было преобразовано во фрактальное с самоподобным спектром (выражение 4) и была построена его структурная функция (рисунок 2 (а)). В данном случае распределение значений функции близко к степенному, но наблюдается отклонение в области высоких частот. Для компенсации этого отклонения можно провести декомпозицию полученного спектрально-самоподобного изображения при помощи вейвлет-преобразований, домножить изображение, на котором представлена область высоких частот, на некий числовой коэффициент и вновь сложить элементы декомпозиции в цельное изображение. После перечисленных операций структурная функция принимает вид, как на рисунке 2 (б) – в этом случае отклонение значений от степенного закона статистически незначительно и можно сказать, что структурная функция изображения самоподобна.

Для проверки эффективности предлагаемых в работе методов анализа фрактальных свойств программными средствами моделировались реализации случайного двумерного Броуновского поля, а так же использовались фрактальные изображения, полученные методом Фурье-фильтрации. В обоих случаях в результате моделирования получали изображение с заданной фрактальной размерностью d= 2.5. Для каждой реализации рассчитывалось глобальное значение показателя Херста (a₂) на всем изображении и среднее значение поля распределения локальных значений . Для фрактального изображения модуль разности между этими двумя значениями  должен быть незначительным.

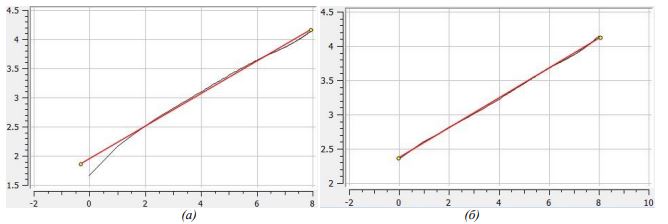
Рис. 2 – Структурная функция изображения CoNiP, после преобразования в спектрально самоподобное (а) и после дополнительной фильтрации при помощи вейвлетов (б)

В результате тестирования разработанного программного решения на выборке моделей фрактальных изображений объемом  N = 1000 было установлено, что для модели случайного Броуновского поля искомые значения в среднем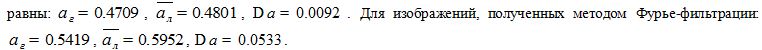 

Используя соотношение зависимости фрактальной размерности от показателя Херста ( d= 3 - a), можно сделать вывод, что расчетные показатели близки к заданным при моделировании. Полученные результаты позволяют заключить, что при использовании предлагаемых методов глобальные значения показателя Херста на исследуемых изображениях оказались близки к средним локальным значениям, что свидетельствует о статистически правильной оценке фрактальных свойств.

Заключение

В данной работе исследован метод анализа фрактальных свойств изображений, основанный на самоподобии структурной функции (метод Пентланда). Предложена модификация метода с целью оценки фрактальных свойств в локальных областях. В основе модифицированного метода лежит расчет локального значения оценки показателя Херста в окрестности каждого пикселя изображения (используется скользящее окно фиксированного размера).

Рассмотрен метод синтеза спектрально-самоподобного изображения и предложен метод его дальнейшего преобразования во фрактальное с самоподобной структурной функцией.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Старк Г. Статистические методы распознавания образов с использованием признаков, выделенных из оптических фурье-спектров / Г.Старк, Р. О'Тул // Применение методов фурье-оптики. – М.: Радио и связь. – –C. 440 - 472.
2. Потапов А.А. Новейшие методы обработки изображений / А.А.Потапов, Ю.В.Гуляев, С.А. Никитов и др. – М.: Физматлит,2008. – 496 с.
3. Панин С.В. Использование вейвлет-анализа изображений поверхности для изучения процессов пластической деформации и разрушения на мезомасштабном уровне / С.В.Панин, И.В.Шакиров, И.В.Сырямкин и др.// Автометрия. – –Т. 39 – № 1 –C. 37-53.
4. Мандельброт Б. Фрактальная геометрия природы / Б.Мандельброт. – М.: Институт компьютерных исследований, 2002. – 656 с.
5. Грудин Б.Н. Моделирование и анализ изображений с использованием спектральных характеристик /Б.Н.Грудин, В.С.Плотников, Е.В.Пустовалов и др.// Известия Российской академии наук. Серия физическая. – – Т. 76, №9. – С. 1160-1165.
6. Грудин Б.Н. Моделирование изображений с заданными фрактальными характеристиками / Б.Н.Грудин, В.С.Плотников, Н.А.Смольянинов // Автометрия. – – Т.46, № 3. – С.13-21.
7. Грудин Б.Н. Синтез фрактальных микроскопических изображений / Б.Н.Грудин, В.С.Плотников, Н.А. Смольянинови др.// Изв. Вузов. – – № 11. – С.85-91.
8. Грудин Б.Н. Обработка и моделирование микроскопических изображений / Б.Н.Грудин, В.С.Плотников. – Владивосток: Дальнаука, 2010. – 349 с.
9. Грудин Б.Н. Фрактальная фильтрация микроскопических изображений/ Б.Н.Грудин, В.С.Плотников, Н.А.Смольянинов и др.// Известия высших учебных заведений. Физика. – 2010. –№ 3/2. – С.71-76.
10. Кулешов Е.Л. Использование вейвлет-преобразования для оптимального оценивания тренда случайного процесса / Е.Л.Кулешов, В.К. Фищенко // Автометрия. – – Т. 39, № 1. –C. 108-113.

Список литературы на английском языке / ReferencesinEnglish

1. Stark G. Statisticheskie metody raspoznavanija obrazov s ispol'zovaniem priznakov, vydelennyh iz opticheskih fur'e-spektrov [Statistical methods for pattern recognition using features extracted from optical fourier spectra] /G.Stark, R. O'Tul // Primenenie metodov fur'e-optiki [Application of Fourier optics methods]. – M.: Radio i svjaz'. – 1988. – P. 440 - 472. [in Russian]
2. Potapov A.A., Guljaev Ju.V., Nikitov S.A., Pahomov A.A., German V.A. Novejshie metody obrabotki izobrazhenij [The latest image processing techniques]. – M.: Fizmatlit, 2008. – 496 p. [in Russian]
3. Panin S.V. Ispol'zovanie vejvlet-analiza izobrazhenij poverhnosti dlja izuchenija processov plasticheskoj deformacii i razrushenija na mezomasshtabnom urovne [Using wavelet analysis of surface images to study the processes of plastic deformation and fracture at the mesoscale level] /A.A. Potapov, Ju.V. Guljaev, S.A. Nikitov et al. // Avtometrija. – 2003. – 39 – № 1 – P. 37-53. [in Russian]
4. Mandel'brot B. Fraktal'naja geometrija prirody [Fractal geometry of nature] /B.Mandel'brot. – M.: Institut komp'juternyh issledovanij, 2002. – 656 p. [in Russian]
5. Grudin B.N. Modelirovanie i analiz izobrazhenij s ispol'zovaniem spektral'nyh harakteristik [Modeling and analysis of images using spectral characteristics] /B.N.Grudin, V.S. Plotnikov, E.V. Pustovalov et al. // Izvestija Rossijskoj akademii nauk. Serija fizicheskaja [Bulletin of the Moscow university. Physical series]. – 2012. – V. 76, №9. – P. 1160-1165. [in Russian]
6. Grudin B.N. Modelirovanie izobrazhenij s zadannymi fraktal'nymi harakteristikami [Modeling images with specified fractal characteristics] /B.N.Grudin, V.S. Plotnikov, N.A. Smol'janinov // Avtometrija. – 2010. – V.46, № 3. – P.13-21. [in Russian]
7. Grudin B.N. Sintez fraktal'nyh mikroskopicheskih izobrazhenij [Synthesis of fractal microscopic images]/B.N.Grudin, V.S. Plotnikov, N.A. Smol'janinov et al. // Izv. Vuzov. – 2009. – № 11. – P.85-91. [in Russian]
8. Grudin B.N. Obrabotka i modelirovanie mikroskopicheskih izobrazhenij [Processing and modeling of microscopic images]/B.N.Grudin, V.S. Plotnikov. – Vladivostok: Dal'nauka, 2010. – 349 p. [in Russian]
9. Grudin B.N. Fraktal'naja fil'tracija mikroskopicheskih izobrazhenij [Fractal filtering of microscopic images] / N.Grudin, V.S. Plotnikov, N.A. Smol'janinov et al.// Izvestija vysshih uchebnyh zavedenij. Fizika [Bulletin of higher educational institutions. Physics]. –2010. –№ 3/2. – P.71-76. [in Russian]
10. Kuleshov E.L. Ispol'zovanie vejvlet-preobrazovanija dlja optimal'nogo ocenivanija trenda sluchajnogo processa [Using the wavelet transform for optimal estimation of the trend of a random process] /E.L.Kuleshov, V.K. Fishhenko // Avtometrija. –2003. – V. 39, № 1. – P. 108-113. [in Russian]