ПОИСК РЕШЕНИЙ В ПРОДУКЦИОННЫХ СИСТЕМАХ МЕТОДАМИ ОБОБЩЕННОГО ПРОГРАММИРОВАНИЯ

ПОИСК РЕШЕНИЙ В ПРОДУКЦИОННЫХ СИСТЕМАХ МЕТОДАМИ ОБОБЩЕННОГО ПРОГРАММИРОВАНИЯ

Научная статья

Русакова З.Н.*

Московский государственный технический университет им. Н. Э. Баумана, Россия, Москва

* Корреспондирующий автор (z.n.rusakova[at]mail.ru)

Аннотация

В настоящее время активное развитие получает концепция создания базовых элементов систем искусственного интеллекта. В работе рассматриваются вопросы разработки алгоритмического и программного инструментария экспертных систем искусственного интеллекта, основным компонентом которых является блок логического вывода. Предлагается шаблон интерпретатора для решения задач моделирования продукционных систем в пространстве состояний c прямым и обратным логическим выводом на основе метода поиска в глубину. Средствами обобщенного программирования разработана полиморфная иерархия классов С++, реализующих основные алгоритмы вывода, на основе стратегии формирования списков открытых и закрытых вершин.

Ключевые слова: граф, списки, обобщенное программирование, поиск, деревья, шаблоны, классы, правила продукции, динамические структуры.

SEARCHING FOR SOLUTIONS IN PRODUCTION SYSTEMS VIA GENERIC PROGRAMMING METHODS

Research article

Rusakova Z.N.*

Bauman Moscow State Technical University, Russia, Moscow

* Corresponding author (z.n.rusakova[at]mail.ru)

Abstract

Currently, the concept of creating the basic elements of artificial intelligence systems is being actively developed. The article deals with the development of algorithmic and software tools for AI expert systems, the main component of which is inference. The study proposes an interpreter template for solving problems of modeling production systems in the state space with forward and backward chaining based on the depth-first searching method. Based on the strategy of creating lists of open and closed vertices, the study develops a polymorphic hierarchy of C++ classes that implement the main inference algorithms by means of generic programming.

Keywords: graph, lists, generic programming, search, trees, templates, classes, product rules, dynamic structures.

Введение

Активное развитие в настоящее время экспертных систем искусственного интеллекта требует создания алгоритмического и программного инструментария, обеспечивающего быстродействие при обработке больших массивов данных. Решение поставленных задач обеспечивается средствами объектно - ориентированного языка С++.

В продукционных системах знания представляются с помощью набора правил продукций. Под продукцией понимается выражение следующего вида: < I, A→B >, где I идентификатор правила (например, порядковый номер), А -посылка правила, В - заключение; A→B является ядром правила-продукции [1], [2], [3]. Посылка является множеством условий, связанных логической связкой "И" ". Для решения используется аппарат теории графов. Правила продукции представляются графами И-ИЛИ. Логический вывод в продукционных системах соответствует поиску решений в И-ИЛИ графах. Если правила-продукции не содержат в условной части конъюнкций, то вывод в продукционных системах будет соответствовать поиску решений в пространстве состояний.

В качестве формальной модели описания графа (или базы правил) в пространстве состояний используется представление графа списком ребер [4], [5], [6]. В пространстве состояний правило представляется направленным ребром графа. База правил соответствует списку ребер графа. Семантические определения вершин задается в словаре, в котором каждой вершине ставится в соответствие понятие предметной области. Правила базы знаний формулируются в терминах понятий предметной области.

Ребро графа описывается классом Rebro [7], полями которого объявляются начальная и конечные вершины - firstNum, lastNum, номер правила - num_p, метка ребра, которая изначально равна 0, при включении ребра в дерево решения метка устанавливается в 1. В конструктор класса передаются параметры для инициализации.

class Rebro { public: int firstNum, lastNum, num_p, metka; Rebro(){} Rebro(int fn, int ln, int vs):firstNum(fn), lastNum(ln), num_p (vs), metka(0){} };

Вершина описывается классом Node [7], полями которого объявляются целые числа – номер вершины (num) и поле flag, определяющее выбор вершины в процессе поиска. Целью работы является разработка шаблона интерпретатора для решения задач моделирования продукционных систем в пространстве состояний. Ниже описывается проектирование полиморфной иерархии классов, реализующих основные алгоритмы прямого и обратного вывода, на языке С++, позволяющего осуществить распараллеливание вычислений и повысить быстродействие [6]. Для программной реализации используются обобщенные динамические структуры – списки [6], [7], [8].

Алгоритм решения

В основе алгоритмов логического вывода в интерпретаторах систем продукций используются классические методы обработки графов - поиск в ширину и в глубину. При решении задач поиска в графах вводится понятие открытых и закрытых вершин или белые, серые и черные вершины [1], [3], [5]. Вершины графа изначально раскрашиваются одинаково - все вершины белые. При открытии вершины она становится серой. Вершина – открытая, пока не порождены ее потомки. Эти вершины составляют фронт вершин, являющихся потомками вершины раскрытия. Вершина –закрытая, если в процессе поиска порождены все ее потомки. В этом случае вершина становится черной.

Эти вершины хранятся и обрабатываются в двух списках поиска: список открытых вершин и список закрытых вершин. Вершины графа в процессе поиска из списка открытых переписываются в список закрытых или черных. Методы поиска в ширину и в глубину отличаются стратегией выбора узлов для раскрытия из списков открытых вершин. Стратегия метода поиска в ширину реализуется по принципам моделирования очереди: вершина для раскрытия выбирается из головы списка открытых вершин, а потомки записываются в хвост списка открытых [4], [7], [10]. В стратегии поиска в глубину используется механизм стека: вершина для раскрытия выбирается из головы списка открытых вершин, потомки записываются в голову. В первом случае дерево решения формируется в списке открытых вершин, во втором- в списке закрытых вершин. В работе [7] описывается разработанный шаблон поиска использующий метод поиска в ширину. В данной статье рассматривается проектирование класса поиска на основе метода в глубину. В основе стратегии лежит механизм стека: первый вошел – первый вышел (LIFO), который используется при формировании списков открытых вершин [1], [4], [6].

Списки открытых и закрытых вершин и список, описывающий граф сети, создаются на основе методов разработанного шаблонного класса List [7], [8], [9], моделирующего двунаправленные списки объектов. В классе List определяются адресные поля: указатели на первое и последнее звено, и реализованы основные методы обработки списков: добавить в голову, добавить в хвост, взять из головы, взять из хвоста, просмотр списка.

template < class T > class List { public: Elem <T> * first,* last,* cur; List<T>()               {first=0; last=0; cur=0; } // прототипы основных методов void add (T temp ); //добавить в хвост void add_head ( T temp); //добавить в голову void del_xwost() ; //удалить из хвоста void del_head ( ); // удалить из головы };

Реализация методов класса приводится в [7], [8], [9]. Звено списка описывается шаблонным классом Elem с информационным полем, тип которого передается как параметр, и двумя указателями [7], [8], [9].

На основе обобщенных классов C++ разработана иерархия классов моделирования продукционных систем как решение поисковых задач в графах [7]. Базовый класс в иерархии – обобщенный класс Poisk_graf. В потомках этого класса реализуется различные алгоритмы поиска [7]. Полями класса Poisk_graf объявляются списки открытых и закрытых вершин и список ребер, описывающий граф:

List <Tr> listOpenNodes; List <Tr> listCloseNodes; List <T> sreb;

Параметрами шаблона являются классы, описывающие ребра (правила) графа – класс Rebro и вершины – класс Node [7]. В конструктор класса с параметрами передаются аргументы: список описания графа, вершина источника и целевая вершина. В конструкторе класса вызываются конструкторы создания списков открытых и закрытых вершин и выполняется их инициализация.

template < class T , class Tr > class Poisk_graf { public: int flagys, flagnot, incep, cel ; List <Tr> listOpenNodes; //список открытых вершин List <Tr> listCloseNodes; // список закрытых вершин List <T> sreb; //список ребер – правила продукции //конструкторы Poisk_graf <T, Tr > (){} Poisk_graf <T, Tr> ( List <T> p, int inw, int celw){ sreb = p;        incep=inw; cel= celw; flagys=1, flagnot=1; listOpenNodes=List <Tr>(); listOpenNodes.add(incep); listCloseNodes=List <Tr>(); } };

В основе всех методов поиска лежит поиск по образцу, целью которого является порождение потомков вершины, выбранной для раскрытия. В алгоритме поиска в глубину вершина раскрытия выбирается из головы списка открытых вершин. При поиске в глубину находится один из возможных потомков. Возможный выбор определяется различными критериями, которые определяют количество итераций достижения решения. В простейшем случае этот потомок – вершина первого ребра, инцидентного вершине раскрытия. Построение дерева решения и поиск достижимых вершин выполняется по следующему алгоритму.

Пока список открытых вершин не пуст или целевая вершина не достигнута на каждом шаге цикла выполнить:

Из головы списка открытых вершин извлекается вершина, которая становится текущей подцелью, для нее вызывается метод поиска по образцу и определяется потомок. Для потомка проверяются условия:

если цель достигнута - выход из цикла поиска;

если потомок в поиске по образцу не найден (вершина не раскрывается) и список открытых вершин не пуст, то вершина, для которой порождали потомка, из списка открытых вершин удаляется и записывается в список запрещенных вершин, который соответствует в поиске в глубину списку закрытых;

если потомок в поиске по образцу не найден и в списке открытых вершин - только начальная вершина поиска, что соответствует варианту обходу графа в случае, если решение не найдено;

если потомок определен и цель не достигнута, то запись потомка в голову списка открытых вершин;

Ниже описывается шаблонный класс - потомок базового класса, в двух методах которого определяется список вершин и правил решения модифицированным методом поиска в глубину, в котором при выборе потомка проверяются перечисленные ниже условия.

template < class T , class Tr> class Poisk_graf_potomok_gl:                public Poisk_graf <T,Tr>{ public: // конструкторы Poisk_graf_potomok_gl <T, Tr > (){} Poisk_graf_potomok_gl <T, Tr> ( List <T> p, int inw, int celw): Poisk_graf(p, inw,celw){} int potomki (); // метод - поиск по образцу int poisk (); // метод – поиск в глубину };

В методе класса potomki () выполняется поиск по образцу, в методе - poisk() – алгоритм поиска в глубину. Поиск по образцу выполняется в цикле просмотра ребер графа. Для поиска потомка в цикле просматривается список ребер графа. Найденная вершина записывается в голову списка открытых вершин. На каждом шаге цикла проверяется выполнение одного из условий:

проверка совпадения вершины раскрытия с начальной вершиной и определения конечной как целевой. В этом случае получено решение и устанавливается значение флага поиска, определяющего решение;

если потомок не целевая вершина, то для выбора вершины подцели на следующий шаг поиска необходимо выполнение условий:

ребро, инцидентное вершине, еще не было просмотрено (его метка равна 0), и следующая подцель не входит в список запрещенных вершин,

если условия выполняются, то вершина потомок записывается в голову списка открытых вершин и выполняется выход из цикла поиска образца.

Описание метода поиска по образцу в классе потомке:

template < class T , class Tr> int Poisk_graf_potomok_gl <T,Tr >:: int potomki (){ int i,j, k,flag;                flag=1; j=0; sreb.cur=sreb.first; // начало списка базы правил //определяется первый потомок while ( sreb.cur && flag==1 && j==0)           { if( listOpenNodes.first->data.num ==sreb.cur->data.firstNum && sreb.cur->data.lastNum ==cel && sreb.cur->data.metka==0){ flagys =0; j++; flag=0; } // нашли цель - вышли из цикла else // определение потомка - и запись в голову списка if(listOpenNodes.first->data.num==sreb.cur->data.firstNum && sreb.cur->data.metka==0 )               { listOpenNodes.add_head(sreb.cur->data.lastNum); sreb.cur->data.metka=1; // ребро в списке ребер помечается как пройденное j++;       flag=0; } // выход из цикла просмотра sreb.cur=sreb.cur->next; // переход к следующему ребру } return j; }

В методе поиска в глубину используются результаты метода поиска по образцу. Построение дерева решения и поиск достижимых вершин выполняется в методах класса по вышеописанному алгоритму.

Пока список открытых вершин не пуст или целевая вершина не достигнута, на каждом шаге цикла вызывается метод поиска по образцу и определяется потомок, который заносится в голову списка открытых вершин. Если потомок в поиске по образцу не найден (вершина не раскрывается) (выполняются условия: j=0 и решения нет - flagys=1) и список открытых вершин не пуст, то вершина, для которой порождали потомка, из списка открытых вершин удаляется и записывается в список запрещенных вершин. Если потомок определен и цель не достигнута, то продолжение цикла поиска.

template < class T , class Tr>

 int Poisk_graf_potomok_gl <T,Tr >:: int poisk() {

 int i,j,k, n;     listCloseNodes.first=0;

 while ( flagys && flagnot )      {

         j=potomki (); // определение потомка

         if ( flagys==0 ){  return 1; }

         else if ( flagys && j==0 && listOpenNodes.first->next!=0 ) {

         //запись в список закрытых вершин

listCloseNodes.add_head(listOpenNodes.first->data.num); listOpenNodes.del_head(); }

         else // нет решения

 if ( j==0 && listOpenNodes.first->next==0 &&

listOpenNodes.first->data.num ==incep) {

 flagnot=0; return 0; }

 }

}

Для тестирования

методов поиска в глубину и построения решения объявляется экземпляр переменной класса:

Poisk_graf_potomok_gl < Rebro ,Node> graf;

Вызывается конструктор класса, которому передаются параметры: список ребер, начальная и целевая вершины:

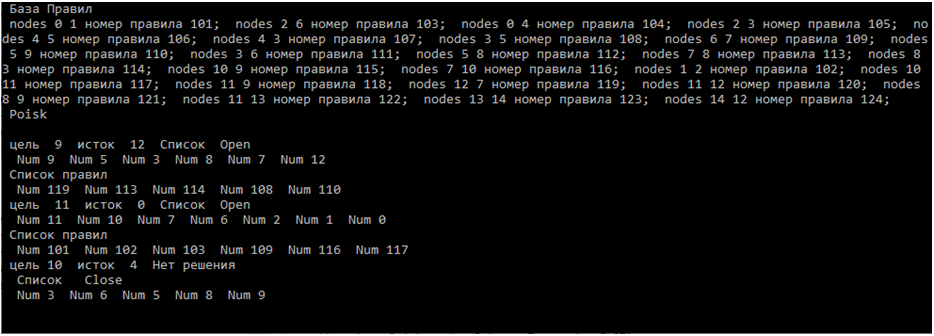
graf = Poisk_graf_potomok_gl < Rebro, Node>(<список аргументов>); после вызова конструктора и инициализации вызывается метод поиска. Результаты тестирования фрагмента базы правил приведены ниже.

Рис. 1 – Результаты тестирования фрагмента базы правил

 

Решение – вершины пути содержатся в списке открытых вершин, правила – в списке правил.

Заключение

На основе обобщенного программирования С++ разработан шаблон интерпретатора для решения задач моделирования продукционных систем в пространстве состояний. Используемая стратегия методов поиска решения и выбранная платформа С++ эффективнее других с точки зрения быстродействия и возможности использования потоков для распараллеливания вычислений. Программный инструментарий является основой для разработки интерпретаторов в графах И-ИЛИ и системах нечеткого вывода.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Новиков Ф.А Символический искусственный интеллект: математические основы представления знаний / Ф.А Новиков. Москва: Издательство Юрайт, 2019,278
2. Седжвик Р. Алгоритмы на C++. Фундаментальные алгоритмы и структуры данных / Р. Седжвик. – М.: Вильямс, 2013. – 1056 с.
3. Кормен Т. Алгоритмы: построение и анализ, 3-е изд / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. – М.: Вильямс, 2013. – 1328 с.
4. Касьянов В.Н. Графы в программировании: обработка, визуализация и применение / В.Н. Касьянов, В.А. Евстигнеев. – СПб.: БХВ-Петербург, 2003. 1104 с.
5. Страуструп – 1999 Страуструп Б. Язык программирования C++. СПб.: Бином, 1999. c. 990.
6. Джоши Пратик Искусственный интеллект с примерами на Python / Пратик Джоши Пер. с англ. - СПб. : ООО "Диалектика", 2019. - 448 с. –
7. Русакова З.Н. Применение обобщенного программирования для решения поисковых задач в графах / З.Н. Русакова // Журнал Тенденции развития науки и образования. Апрель 2020 г. №60, Часть 2 Изд. НИЦ «Л-Журнал»,
8. Русакова З.Н. Динамические структуры данных и вычислительные алгоритмы Visual C++ / З.Н. Русакова. Санкт-Петербургбург.2014, 272 с.
9. Русакова З.Н. Структуры данных в С++ / З.Н. Русакова, И.В Рудаков. Москва: Издательство МГТУ им. Н.Э Баумана.2020, c157.
10. Русакова З.Н., Разработка инструментальных средств для решения задач принятия решений / З.Н. Русакова // Интеллектуальные системы. Труды Девятого международного симпозиума, М., РУСАКИ, 2010, 773

Список литературы на английском языке / References in English

1. Novikov F.A. Simvolicheskij iskusstvennyj intellekt: matematicheskie osnovy predstavlenija znanij [Symbolic artificial intelligence: mathematical foundations of knowledge representation] / F.A Novikov. – Moscow: Yurayt Publishing House, 2019, 278. [in Russian]
2. Sedgwick R. Algoritmy na C++. Fundamental'nye algoritmy i struktury dannyh [Algorithms in C ++. Fundamental algorithms and data structures] / R. Sedzhvik. - M .: Williams, 2013 .-- 1056 p. [in Russian]
3. Cormen T. Algoritmy: postroenie i analiz [Algorithms: construction and analysis] / T. Kormen, Ch. Lejzerson, R. Rivest, K. Shtajn, 3rd ed. - M .: Williams, 2013 .-- 1328 p. [in Russian]
4. Kasyanov V.N. Grafy v programmirovanii: obrabotka, vizualizacija i primenenie [Graphs in programming: processing, visualization and application] / V.N. Kas'janov, V.A. Evstigneev. - SPb .: BHV-Petersburg, 2003.1104 p. [in Russian]
5. Straustrup – 1999 Straustrup B. Jazyk programmirovanija C++. [Stroustrup - 1999 Stroustrup B. C ++ programming language]. SPb .: Binom, 1999. p. 990. [in Russian]
6. Joshi Practice [Artificial intelligence with examples in Python] / Pratik Dzhoshi transl. from English - SPb. : LLC "Dialectics", 2019. - 448 p. -[in Russian]
7. Rusakova Z.N. Primenenie obobshhennogo programmirovanija dlja reshenija poiskovyh zadach v grafah [Application of generalized programming for solving search problems in graphs] / Z.N. Rusakova // Zhurnal Tendencii razvitija nauki i obrazovanija. [Journal of Trends in the development of science and education]. April 2020 No. 60, Part 2 Ed. Research Center "L-Journal",[in Russian]
8. Rusakova Z. N. Dinamicheskie struktury dannyh i vychislitel'nye algoritmy Visual C++ [Dynamic data structures and computational algorithms of Visual C ++] / Z.N. Rusakova. St. Petersburg. 2014, 272 p. [in Russian]
9. Rusakova Z. N. Struktury dannyh v S++ [Data structures in C ++] / Z.N. Rusakova, I.V Rudakov. Moscow: Publishing house MSTU im. N.E Bauman. 2020, p 157. [in Russian]
10. Rusakova Z.N., Razrabotka instrumental'nyh sredstv dlja reshenija zadach prinjatija reshenij [Development of tools for solving decision-making problems] / Z.N. Rusakova // Intellektual'nye sistemy. Trudy Devjatogo mezhdunarodnogo simpoziuma [Intelligent systems. Proceedings of the Ninth International Symposium], M., RUSAKI, 2010, 773. [in Russian]