ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ОСЕВЫХ ЛИНИЙ ГОРНЫХ ЛЕДНИКОВ

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ОСЕВЫХ ЛИНИЙ ГОРНЫХ ЛЕДНИКОВ

Научная статья

Рыбак О.О. *

ORCID: 0000-0003-3923-7163,

Сочинский научно-исследовательский центр РАН, Сочи, Россия,

Филиал Института природно-технических систем, Сочи, Россия;

Институт водных проблем РАН, Москва, Россия,

* Корреспондирующий автор (o.o.rybak[at]gmail.com)

Аннотация

Прогностические расчеты изменений состояния горного оледенения эффективно осуществляются методами математического моделирования. Применение трехмерных моделей, учитывающих все виды напряжений, требует больших затрат вычислительных ресурсов, что создает объективные сложности при расчетах эволюции оледенения целых горных систем.  Это определило рост интереса к относительно простым моделям, в том числе к одномерным, так называемым «flow-line models», то есть к моделям, имитирующим изменения характеристик ледников вдоль осевых линий. Осевые линии строятся либо, фактически, вручную, либо с применением достаточно сложных и затратных (полу-) автоматических методов. В настоящей статье предложен простой алгоритм построения осевых линий горных ледников для последующего использования в прогностических численных экспериментах. Алгоритм апробируется на нескольких горно-долинных ледниках различных конфигураций.

Ключевые слова: горный ледник, течение льда, осевая линия ледника.

DETERMINING AXIAL LINES POSITION OF MOUNTAIN GLACIERS

Research article

Rybak O.O. *

ORCID: 0000-0003-3923-7163,

Sochi Research Center of the Russian Academy of Sciences, Sochi, Russia;

Branch of Institute of Natural and Technical Systems, Sochi, Russia;

Water Problems Institute of the Russian Academy of Sciences, Moscow, Russia

* Corresponding author (o.o.rybak[at]gmail.com)

Abstract

The paper presents predictive calculations of changes in the state of mountain glaciation based on the mathematical modeling methods. The use of three-dimensional models that take into account all types of stresses requires large computational resources, which creates objective difficulties in calculating the evolution of the glaciation of entire mountain systems. This fat has determined the growing interest in relatively simple models, including one-dimensional, so-called “flow-line models”, that is, models that simulate changes in the characteristics of glaciers along the centerlines. Axial lines are built either, in fact, manually, or using fairly complex and costly (semi-) automatic methods. This article proposes a simple algorithm for constructing the axial lines of mountain glaciers for subsequent use in predictive numerical experiments. The algorithm was tested on several mountain-valley glaciers of various configurations.

Keywords: mountain glacier, ice flow, glacial centerline.

Введение

Горное оледенение играет важную роль в стабильном снабжении водой обширных прилегающих территорий. Существуют разные оценки вклада талой ледниковой воды в общий речной сток, которые варьируются от региона к региону. В условиях меняющегося климата состояние горного оледенения вызывает обоснованное беспокойство, о чем косвенно свидетельствует рост числа публикаций, посвященных оценкам изменения характеристик оледенения за последние несколько десятков лет и их прогнозу. Очевидно, что объективные проекции изменений параметров оледенения возможно построить только применяя методы математического моделирования. Парадокс заключается в том, что усложнение математических моделей, в конечном итоге, снижает возможности их применения из-за роста затрат на вычисления, которое опережает рост производительности компьютеров. Последнее обстоятельство определило рост интереса к относительно простым моделям, в том числе к одномерным, так называемым «flow-line models», то есть к моделям, имитирующим изменения характеристик ледников вдоль осевых линий [1]. Особый интерес представляет работа [2], в которой даны прогностические оценки изменений ледникового стока для более, чем половины горно-ледниковых бассейнов планеты. Для расчетов была использована упрощенная модель [3], которая при всех допущениях позволила сделать достаточно объективную оценку изменений параметров оледенения в рассматриваемых бассейнах до конца текущего столетия. Используя модифицированную версию модели [3], авторы работы [4] дали детальный прогноз изменения всех ледников Альп. Одной из ключевых задач применения простых моделей [1], [2], [4] является определение осевых линий ледников, вдоль которых рассчитываются изменения толщины льда. Алгоритм расчетов эволюции ледников [5], впоследствии подвергшийся неоднократным усовершенствованиям, базируется на заданном положении осевых линий. Сами же детали процедуры расчета положения осевых линий в процитированных работах не приводятся.  Существует несколько алгоритмов различной сложности для подобных расчетов [7], [8], [9], однако их реализация в виде программного кода достаточно трудоемка, особенно если учесть те требования, которые обусловлены конкретными условиями нашего исследования – совместимостью с уже существующими процедурами (в частности, расчета баланса массы и течения льда), написанными на языке ФОРТРАН относительно ранних версий (90/95) (и, соответственно, имеющимися ограничениями на выполнение тех или иных операций).

Одна из конечных целей нашего исследования заключается в более точном, чем это было сделано в [2], прогнозе изменений ледникового стока на длительную перспективу. Для этого потребовалось модифицировать базовую модель [3], в частности, включить в нее описание теплообмена участков ледников, покрытых моренным чехлом, что актуально, например для Кавказа [10], и чем пренебрегают авторы работ [2], [3], [4]. Первым шагом в достижении поставленной цели является полуавтоматическое построение осевых линий и интерактивном режиме, чему, собственно, посвящена настоящая статья. Ключевая идея определения положения осевых линий – через расчет «штрафной функции» («penalty function») взята нами из работы [7], однако, сама методика расчетов, адаптированная к задачам нашего исследования, полностью оригинальна. Заметим, что банальная, казалось бы, с геометрической точки зрения задача на самом деле не является такой в случае дискретного представления как контуров ледника, так и осевых линий на регулярной пространственной сетке.

Валидация разработанного алгоритма произведена на нескольких ледниках различных конфигураций.

Описание алгоритма и его тестирование

Для разработки алгоритма нахождения осевых линий ледников необходимо, естественно, дать определение того, что, собственно, нужно найти. В конечно-разностном представлении граница ледника и его осевые линии представляют собой набор точек. На регулярной пространственной сетке расстояние между соседними точками одинаковое. Следовательно, осевая линия ледника должна представлять собой набор узлов регулярной сетки, расстояние от которых до точек, расположенных на внешнем контуре ледника, минимально. Очевидно, что для подавляющего числа точек минимальное расстояние от осевой линии до границы ледника будет находиться на нормали, проходящей через данную точку на осевой линии. Однако в прифронтовой области, где расстояние до языка ледника меньше, чем его ширина, это условие, естественно, нарушается.

Воспользуемся простой процедурой, описанной в [7], и модифицированной для нашей задачи. Задача решается в три этапа, каждый из которых состоит из следующих шагов. Этап первый:

1. Определение набора граничных точек.
2. Сглаживание контура ледника. Сглаживание сводится к удалению граничных точек, которые в дальнейшем не позволят провести автоматическую сквозную нумерацию.
3. Последовательная нумерация оставшихся точек. Для этого применяется следующий простой алгоритм. Мы исходим из того, что линия, оконтуривающая ледник, не может ветвиться, соответственно, каждая точка на контуре может граничить только с двумя окружающими – с предшествующей и последующей.
4. Первой граничной точке присваивается №1, и эта точка исключается из дальнейшего рассмотрения. Далее перебираются восемь окружающих ее точек. Той из них, которая оказывается граничной, присваивается №2, точка помечается, - на этом текущий цикл перебора прерывается, новый цикл начинается с точки №2 и процедура повторяется. Для того, чтобы процесс не прерывался, необходимо выполнить описанный выше третий шаг. В результате получаем последовательность граничных точек.
5. Определение координат максимумов и минимумов высоты поверхности на контуре ледника, то есть точек старта и финиша осевых линий. Очевидно, что конечным должен быть узел сетки, где абсолютная высота поверхности ледника минимальна. В случае, если речь идет об одном леднике долинного типа, то эта точка будет единственной, и определить ее положение не представляет труда. В случае, если речь идет о ледниковом комплексе, например, о ледниковом комплексе Эльбруса, который состоит из более, чем двух десятков ледников, число таких точек, естественно, будет не меньше числа ледников, входящих в ледниковый комплекс. Другой пример – ледник Джанкуат на северном склоне Главного Кавказского хребта, имеющий общую область питания с ледником Лекзыр на южном склоне. В случае, если рассматривать эти два ледника как единый комплекс, речь должна идти о нахождении нескольких локальных минимумов высоты поверхности, расположенных на контуре ледников, из которых состоит комплекс. Кроме того, в двух приведенных примерах алгоритм поиска локальных максимумов, то есть точек начала осевых линий будет отличаться от соответствующего алгоритма для горно-долинных ледников. В последнем случае он будет относительно более простым: последовательный перебор всех узлов на контуре ледника и сравнение высоты в очередном узле с высотами в точках, расположенных справа и слева на расстоянии n шагов. Выбор n, по всей видимости, достаточно произволен. С одной стороны, n не может быть слишком маленьким, чтобы избежать ложных максимумов, и слишком большим, что, наоборот, может привести к потере реальных максимумов. Предварительные расчеты показали, что при n=5-10 при пространственном разрешении 25 м число найденных локальных максимумов остается неизменным. Тем не менее, диапазон n, при котором число найденных максимумов остается неизменным, может быть иным при другом пространственном разрешении или при более сложной конфигурации ледников, чем тех, что были исследованы в настоящей работе.

На втором этапе в каждом узле сетки i, занятой льдом, рассчитаем так называемую «штрафную» функцию («penalty function» [7]):

где d_i – эвклидово расстояниние от узла сетки i до ближайшей точки на контуре ледника, max(d) – максимальное эвклидово расстояние от какого-либо узла до ближайшей точки на контуре, max(z) и min(z) – максимальная и минимальная абсолютная высота ледника. Множители f₁ и f₂ предназначены для перерасчета безразмерных нормированных величин к масштабу реальных ледников. Выбор этих множителей зависит от геометрических характеристик конкретного ледника. Их значения несущественно меняются для ледников, схожих по размеру, поэтому для единообразия и сопоставимости результатов будем использовать значения для ледника Марух  f₁ = 525 и f₂ = 633 в качестве постоянных (f₁ – максимальное расстояние от узла сетки до ближайшей точки на контуре ледника,  f₂ – максимальный перепад высот на леднике). Параметры a и b определяют относительный вклад расстояния до границы и абсолютной высоты в значения штрафной функции (табл. 1). Выбор значений этих параметров, точнее их соотношение, определяет возможность прокладки осевой линии на отдельных участках ледника, что поясняется на примерах ниже.

В отличие от [7], в дальнейшем будем использовать два типа штрафных функций – полную (Р₁) – как определено в ур. (1) и сокращенный вариант последней (Р₂) – только первую часть правой части ур. (1). Заметим, что использованные в настоящей работе значения a и b отличаются от тех, которые предложены в [7] (см табл. 1)

До начала расчета штрафной функции выполним пространственное сглаживание поля высоты поверхности ледника, чтобы нивелировать локальные депрессии или возвышенности различного генезиса на поверхности ледника, которые могут в дальнейшем помешать прокладке осевых линий. Пример подобной локальной депрессии показан на рис. 1.

 

Рис. 1 – Локальная депрессия на леднике Бордуу (массив Ак-Шийрак, Внутренний Тянь-Шань)

Примечание: масштабы депрессии сопоставимы с шагом пространственной сетки, и могут повлиять на траекторию осевой линии, если не провести пространственного осреднения поля высоты поверхности ледника

 

На третьем этапе происходит построение осевых линий, которое начинается из найденных точек максимумов высоты поверхности и, параллельно, из точки (или точек) минимума. Как было упомянуто ранее, под линией в данном случае мы подразумеваем набор точек регулярных узлов пространственной сетки. Все линии строятся последовательно. То есть каждая следующая точка линии, k+1, выбирается из множества точек, окружающих точку k. Исключая из множества возможных точек точку k-1, получаем, что число возможных направлений m продолжения осевой линии не превышает семи. Условием выбора точки k+1 является минимум штрафной функции в выбранной точке. Поскольку штрафная функция зависит от двух переменных – расстояния от контура ледника и от абсолютной высоты – очевидно, что выбранная точка k+1 должна быть ниже по течению. В случае, если значение штрафной функции в выбранной точке k+1 выше, чем в точке k, что возможно в случае, если точка k попала в локальный минимум штрафной функции, это потенциально грозит образованием замкнутого цикла выбора очередной точки, и продолжение осевой линии «застревает» на определенном наборе точек. Образование замкнутого цикла преодолевается двумя способами:

- использованием в локальном минимуме штрафной функции усеченного варианта Р₂ (см. ур. (1));

- использование в интерактивном режиме иного набора параметров a и b.

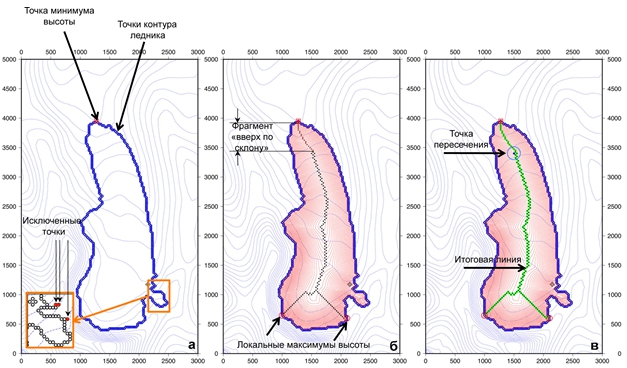
Последовательность расчетов проиллюстрируем на примере ледника Марух (Западный Кавказ), конфигурация которого относительно проста. На рис. 2: (а) определение узлов, пространственной сетки, соответствующих внешнему контуру ледника; красный квадрат обозначает положение узла с минимальной высотой; на врезке – красные точки обозначают узлы, исключенные из контура; (б) красными изолиниями показана штрафная функция с минимальными значениями вдоль предполагаемых осевых линий; красные кружки указывают на положения узлов сетки с локальными максимумами высоты - стартовых точек осевых линий; черные квадраты соответствуют найденным точкам на осевых линиях, начинающихся из точек максимума («течение вниз по склону»); коричневые кружки соответствуют найденным точкам на осевой линии, берущей начало из точки минимума («вверх по склону»); (в) итоговая линия показана зеленым цветом, синим цветом выделена точка, где пересекаются конечные точки линий, берущих начало из точек максимума и минимума.

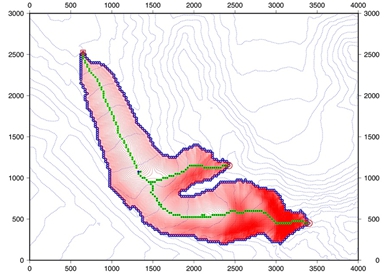
Конфигурация ледника Сары-Тор (массив Ак-Шийрак, Внутренний Тянь-Шань) несколько более сложна, однако разработанный алгоритм хорошо работает и в этом случае (рис. 3).

 

Рис. 2 – Этапы построения осевых линий (на примере ледника Марух, Центральный Кавказ)

Примечание: боковая оцифровка соответствует расстоянию в метрах от условной точки. Синим выделены изолинии абсолютной высоты.  Остальные пояснения даны в тексте

 

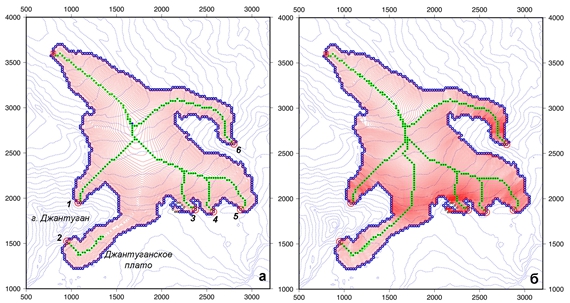
Тестирование алгоритма на леднике Джанкуат с более сложной, чем у ледника Сары-Тор конфигурацией (рис. 4), показало, что оптимальное сочетание параметров a и b в ур. (1) будет разным на разных участках ледника. В связи с этим представляется разумным строить осевые линии не одновременно для всех вершин и для одного и того же набора параметров, а в интерактивном режиме подбирать оптимальное их сочетание для отдельных точек старта.

Очевидно, что при a=2,0 и b=2,0 осевая линия, проходящая по Джантуганскому фирновому плато, «застревает» в области, где штрафная функция имеет локальный минимум (рис. 4а).

 

Рис. 3 – Осевые линии на леднике Сары-Тор (массив Ак-Шийрак, Внутренний Тянь-Шань)

Примечание: обозначения как на рис. 1  

Для того, чтобы преодолеть его необходимо, чтобы вклад абсолютной высоты в штрафную функцию (см. ур. 1) превышал вклад от расстояния до границы ледника (a=2,0 и b=2,3 – рис. 4б). Заметим, что в последнем случае, остальные осевые линии будут нереалистичны.

 

Таблица 1 – Значения параметров a и b в уравнении (1) для отдельных ледников (участков ледников)

Параметр	Марух	Сары-Тор	Джанкуат (оси 1, 3-6)	Джанкуат (ось 2)
a	2,0	2,0	2,0	2,0
b	2,0	2,4	2,0	2,3

   

Рис. 4 – Осевые линии на леднике, проведенные с использованием различных наборов параметров a и b в ур. (1) Джанкуат (Центральный Кавказ)

Примечание: цифрами пронумерованы локальные максимумы абсолютной высоты, в которых берут начало осевые линии (a). Остальные обозначения как на рис. 1. Подробные пояснения даны в тексте

 

Заключительные замечания

В статье был рассмотрен простой алгоритм полуавтоматической прокладки осевых линий горных ледников. Процедура прокладки осевых линий является ключевой для расчета характеристик ледника в упрощенных математических моделях, интерес к которым значительно вырос из-за того, что последние стали активно применяться для расчетов и прогнозов состояния горного оледенения и объемов ледникового стока в масштабах целых горных систем. В дальнейшем мы предполагаем автоматизировать процедуру построения отдельных суб-бассейнов в рамках одного ледника, и перейти к процедуре собственно динамического моделирования.

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Maussion F. The Open Global Glacier Model (OGGM) v1.1 / F. Maussion, A. Butenko, N. Champollion et. al. // Geoscientific Model Development. – 2019. – V. 12. – P. 909-931. https://doi.org./10.5194/gmd-12-909-2019.
2. Huss M. Global-scale hydrological response to future glacier mass loss / M. Huss, R. Hock // Nature Climate Change. – 2018. – V. 8. – P. 135-140. DOI:10.1038/s41558-017-0049-x.
3. Huss M. A new model for global glacier change and sea-level rise [Электронный ресурс] / M. Huss, R. Hock // Frontiers in Earth Science. – 2015. – V. 3. – Article 54. URL: https://www.frontiersin.org/ articles/10.3389 /feart.2015.00054/full. Article 54. DOI:10.3389/feart.2015.00054 (дата обращения 01.10.2019)
4. Zekollari H. Modelling the future evolution of glaciers in the European Alps under the EURO-CORDEX RCM ensemble / H. Zekollari, M. Huss, D. Farinotti // The Cryosphere. – 2019. – V. 13. – P. 1125-1146. https://doi.org/10.5194/tc-13-1125-2019.
5. Farinotti D. A method to estimate the ice volume and ice-thickness distribution of alpine glaciers / D. Farinotti, M. Huss, A. Bauder et al. // Journal of Glaciology. – V. 55(191). – P. 422-430.
6. Huss M. Future high-mountain hydrology: a new parameterization of glacier retreat / M. Huss, G. Jouvet, D. Farinotti, A. Bauder // Hydrology and Earth System Sciences. – 2010. – V. 14. – P. 815-829. DOI:10.5194/hess-14-815-2010.
7. Kienholz С. A new method for deriving glacier centerlines applied to glaciers in Alaska and northwest Canada / C. Kienholz, J.L. Rich, A.A. Arendt, R. Hock R. // The Cryosphere. – 2014. – V. 8. – P. 503-519. DOI:10.5194/tc-8-503-2014
8. Le Bris R. An automatic method to create flow lines for determination of glacier length: A pilot study with Alaskan glaciers / R. Le Bris, F. Paul // Computers & Geosciences. – 2013. – V. 52(3). – P. 234-245. DOI: https://doi.org/10.1016/j.cageo.2012.10.014
9. Le Moine N. A graph-based approach to glacier flowline extraction: an application to glaciers in Switzerland / N. Le Moine, P.-S. Gsell // Computers & Geosciences. – – V. 85(A). – P. 91-101. DOI: https://doi.org/10.1016/j.cageo.2015.09.010
10. Поповнин В.В. Разрастание поверхностной морены на языке ледника Джанкуат за период прямого гляциологического мониторинга / В.В. Поповнин, А.А. Резепкин, Л.Г. Тиелидзе // Криосфера Земли. – 2015. – Т. 19. – №1. – С. 89-98.

Cписок литературы на английском языке / References in English

1. Maussion F. The Open Global Glacier Model (OGGM) v1.1 / F. Maussion, A. Butenko, N. Champollion et. al. // Geoscientific Model Development. – 2019. – V. 12. – P. 909-931. https://doi.org./10.5194/gmd-12-909-2019.
2. Huss M. Global-scale hydrological response to future glacier mass loss / M. Huss, R. Hock // Nature Climate Change. – 2018. – V. 8. – P. 135-140. DOI:10.1038/s41558-017-0049-x.
3. Huss M. A new model for global glacier change and sea-level rise / M. Huss, R. Hock // Frontiers in Earth Science. – 2015. – V. 3. – Article 54. URL: https://www.frontiersin.org/articles/10.3389/feart.2015.00054/full. Article 54. DOI:10.3389/feart.2015.00054 (accessed 01.10.2019)
4. Zekollari H. Modelling the future evolution of glaciers in the European Alps under the EURO-CORDEX RCM ensemble / H. Zekollari, M. Huss, D. Farinotti // The Cryosphere. – 2019. – V. 13. – P. 1125-1146. https://doi.org/10.5194/tc-13-1125-2019.
5. Farinotti D. A method to estimate the ice volume and ice-thickness distribution of alpine glaciers / D. Farinotti, M. Huss, A. Bauder et al. // Journal of Glaciology. – V. 55(191). – P. 422-430.
6. Huss M. Future high-mountain hydrology: a new parameterization of glacier retreat / M. Huss, G. Jouvet, D. Farinotti, A. Bauder // Hydrology and Earth System Sciences. – 2010. – V. 14. – P. 815-829. DOI:10.5194/hess-14-815-2010.
7. Kienholz С. A new method for deriving glacier centerlines applied to glaciers in Alaska and northwest Canada / C. Kienholz, J.L. Rich, A.A. Arendt, R. Hock R. // The Cryosphere. – 2014. – V. 8. – P. 503-519. DOI:10.5194/tc-8-503-2014
8. Le Bris R. An automatic method to create flow lines for determination of glacier length: A pilot study with Alaskan glaciers / R. Le Bris, F. Paul // Computers & Geosciences. – 2013. – V. 52(3). – P. 234-245. DOI: https://doi.org/10.1016/j.cageo.2012.10.014
9. Le Moine N. A graph-based approach to glacier flowline extraction: an application to glaciers in Switzerland / N. Le Moine, P.-S. Gsell // Computers & Geosciences. – – V. 85(A). – P. 91-101. DOI: https://doi.org/10.1016/j.cageo.2015.09.010
10. Popovnin V.V. Razrastanie poverhnostnoj moreny na yazyke lednika Dzhankuat za period pryamogo glyaciologicheskogo monitoringa [Superficial moraine expansion on the Djankuat glacier snout over the direct glaciological mpnitoring period] / V.V. Popovnin, A.A. Rezepkin, L.G. Tielidze // Kriosfera Zemli. – 2015. – V. 19. – No 1. – P. 89-98. [in Russian]