О МЕХАНИЗМЕ ПРОЦЕССОВ ТЯГОТЕНИЯ

О МЕХАНИЗМЕ ПРОЦЕССОВ ТЯГОТЕНИЯ

Научная статья

Кораблев Г.А. *

Ижевская государственная сельскохозяйственная академия, Ижевск, Россия

* Корреспондирующий автор (korablevga[at]mail.ru)

Аннотация

Используя условие стационарного состояния в корпускулярно-волновых взаимодействиях и в рамках нерелятивисткой механики проведен анализ механизма процессов тяготения. Получено уравнение функциональной зависимости постоянной тяготения от электрической постоянной. Предполагается, что тяготение есть волновой вклад от массы заряженных частиц при движении их в поле центральных сил.

Ключевые слова: механизм тяготения, условия стационарного состояния, корпускулярно-волновые процессы.

ON GRAVITATION MECHANISM

Korablev G.A. *

Research article

Izhevsk State Agricultural Academy, Izhevsk, Russia

* Corresponding author (korablevga[at]mail.ru)

Abstract

The analysis of the gravitation process mechanism is carried out using the condition of a stationary state in wave-particle interactions and within the framework of non-relativistic mechanics. The author obtained an equation of the functional dependence of the constant of gravity on the electric constant. It is assumed that gravity is the wave contribution from the mass of charged particles when they move in the field of central forces.

Keywords: gravity mechanism, conditions of the stationary state, particle-wave processes.

Введение

По классической теории тяготения Ньютона сила {\displaystyleF гравитационного притяжения между двумя материальными точками с массами  и , разделёнными расстоянием r, действует вдоль соединяющей их прямой, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними[1]. То есть:

    (1) Здесь G — гравитационная постоянная, равная 6,67408(31)·10⁻¹¹ м³/(кг·с²).

Eсли поле создаётся расположенной в начале координат точечной массой M, гравитационный потенциал определяется формулой:

     (2) В общем случае, когда плотность вещества  распределена произвольно,  удовлетворяет уравнению Пуассона:      (3)

Уравнения Ньютона и Пуассона в рамках нерелятивисткой механики позволяют с большой точностью предсказывать движение небесных тел. В тоже время Ньютоновская модель является чисто математической без какого либо физического содержания[2].

Известно так же, что масса гравитационная и инертная – это одна и та же физическая величина, определяющая разные явления, но динамику которых еще нужно исследовать[3], [4].

Общая теория относительности Эйнштейна (ОТО) объясняет физическую сущность тяготения на основе понятия об изменении геометрических свойств и искривления 4-мерного пространства-времени. В «слабых» гравитационных полях уравнения тяготения Эйнштейна сводятся к уравнению тяготения Ньютона[5].

Однако по современным представлениям «название ОТО является не адекватным и постепенно исчезает из литературы, заменяясь на теорию тяготения» [6]. Появились новые теории, уточняющие исходные принципы ОТО. Наиболее фундаментальной является квантовая теория гравитации[7], но она пока не считается законченной. Тяготение – единственное фундаментальное взаимодействие, по которому пока не построена общепризнанная непротиворечивая теория.

«Применение принципа корпускулярно-волнового дуализма к гравитационному полю показывает, что гравитационные волны можно рассматривать как поток квантов поля — гравитонов. С точки зрения квантовой гравитации, гравитационное взаимодействие осуществляется путём обмена виртуальными гравитонами между взаимодействующими телами»[2].

Идея использования принципов корпускулярно-волнового дуализма для объяснения процессов тяготения через понятие о поле гравитонов [1], [2] представляется наиболее рациональной, хотя предстоит найти основные закономерности механизма этого явления.

Таким образом, проблема физической природы сил тяготения с позиции нерелятивисткой механики нуждается в дальнейшем исследовании. В данной работе делается попытка анализа таких проблем на основе представления о градиенте направленности корпускулярно-волновых процессов в системах различной природы.

Исходные данные

В работе [8] было получено:

1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия, как и приведенная масса, находятся по принципу сложения обратных значений соответствующих величин подсистем. Это – корпускулярный процесс, теоретической концепцией которого может являться энтропия.
2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также соответствующих энергий подсистем. Это – волновой процесс, теоретической концепцией которого может являться негэнтропия.
3. Резонансное стационарное состояние систем выполняется при условии равенства степеней их корпускулярных и волновых взаимодействий. Продукция энтропии в стационарном состоянии полностью компенсируется потоком негэнтропии
4. Приведенные выше положения являются закономерным следствием первого начала термодинамики, анализ которого приведен в работе [8].

Применительно к корпускулярно волновым процессам условие динамического стационарного состояния есть условие равенства их степеней структурных взаимодействий:

   (4) Математически и графически (по номограммам)  стационарное состояние выполняется по уравнению:   (5)

Где, φ = 54°44ˈ- геодезический угол,

α - относительная разность энергетических параметров взаимодействующих систем. Так, например, для постоянной тонкой структуры это уравнение имеет вид:

    (6) Здесь:  

α - постоянная тонкой структуры,

 - энергетические параметры свободных протона и электрона,

 - их энергетические массы,

R – размерная характеристика протона,

r – классический радиус электрона.

Аналогично были получены уравнения для числа π:

    (7)   (8)   Где  g – ускорение свободного падения. Таким образом,  равенство корпускулярных и волновых взаимодействий определяет резонансное стационарное состояние системы. Это условие  соответствует наиболее оптимальным технологическим вариантам  и широко проявляется в природе, а также во фрактальных системах. Корпускулярно-волновой механизм тяготения При вращательном движении твердого тела (или математической точки) вокруг неподвижной оси вектор полного ускорения  состоит из двух составляющих векторов: центростремительного ускорения  и касательного ускорения  - рисунок 1.  

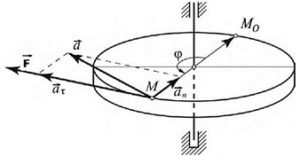
Рис. 1 – Кинематические характеристики вращательных движений

 

Вектор центростремительного ускорения при неподвижной оси вращения направлен к ней, то есть по градиенту поля. Это корпускулярная часть движения. Вектор касательного ускорения направлен от системы по касательной к  траектории, то есть против градиента поля – это волновая часть движения. При равномерном вращении соотношения этих ускорений:

 

Корпускулярно-волновой принцип такого вращательного движения подтверждается уравнением (7).

При аналогичном движении заряженных частиц происходит одновременно перенос ее массы и перенос заряда. Так в электродиффузионном уравнении переноса заряженных частиц общая интенсивность потока (J) равна сумме интенсивностей переноса массы и переноса заряда:

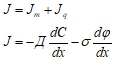
Где dC/dx – градиент концентрации,   – градиент потенциала.

В соответствии с условием стационарного состояния (п.3 исходных данных) действие корпускулярной составляющей определяет появление волновой части процесса. Так круговое движение зарядов (корпускулярный процесс) дает магнитное поле с его полюсами (волновой процесс).При аналогичном движении массы заряженной частицы (корпускулярный процесс) должно возникать потенциальное поле (волновой процесс). Можно предположить, что такое поле является гравитационным, но тогда должно выполняться определенное соотношение между постоянной тяготения и электрической постоянной. Поэтому применительно к кинематике механических систем и сохраняя формализм уравнения (5) получаем:

   (10)

Где, ε₀ - электрическая постоянная,

 – квантовая поправка к гиромагнитному отношению электрона в атоме, которая возможно в данном случае характеризует влияние прецессии движения частиц. Данное уравнение выполняется с отклонением от исходного значения φ на 0,015%.

Таким образом, уравнение (10) подтверждает предположение о том, что волновой вклад массы заряженной частицы определяет наличие гравитационного поля.

Поэтому сходство уравнений Кулона и Ньютона не является формальным, а имеет физическое обоснование. Кроме того равенство гравитационной и инертной массы определяется равенством соответствующих корпускулярных и волновых составляющих. Так: «Если ни от тяготения, ни от инерции избавиться нельзя, можно попробовать считать инерцию и тяготение разными сторонами одного и того же процесса» [9].

Практически есть другой вариант формулы (10):

    (11)

Где K – соотношение исходных корпускулярных и волновых характеристик в данной системе. Возможно, это уравнение для тех случаев, когда исходные характеристики процесса прямо или косвенно уже учитывали логарифмические зависимости.

В работах [10], [11] используется понятие разрушающего напряжения при растяжении пластика нити на шаг ее намотки: σ_α – осевое, σ_β – окружное напряжения, которые заменяются пропорциональной им величиной N_α – осевое «усилие» и N_β – окружное «усилие». При этом выполняется уравнение:

    (12)

«Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия» [10], [11].

В квантовой механике отношение магнитного момента частицы к ее механическому моменту называется магнитомеханическим (гиромагнитным) отношением – g. При этом g_s  2, если магнитный момент электрона обусловлен только спиновой составляющей и g = 1, если он создаётся орбитальным движением электронов. Их соотношение g_s / g  2 и tg²φ = 2 характеризуют соответствующие корпускулярно-волновые зависимости. Более точно с квантовой поправкой g_s / g = 2, 00233.

Сила тяготения не зависит от химического состава тел или частиц. Каждое тело состоит из множества частиц в общем случае разных по природе и по размерам. При образовании гравитационного поля микросистемами, общим для всех структур представляется процесс протон-электронного взаимодействия под действием центральных сил. В неживой природе каждая система частиц, образующих данное тело  может рассматриваться как закрытая. В ней гравитоны изначально имеют направление взаимодействия против градиента поля. В таких случаях (согласно п.2 исходных данных) идет прямое алгебраическое сложение их интенсивностей независимо от химического состава частиц, образующих массу тела. При этом результирующая интенсивность гравитонов прямо пропорциональна массе тела.

Но в живой природе каждая система является открытой, поэтому идут процессы взаимодействия ее с внешней средой, но с сохранением гравитонами специфических особенностей каждой частицы.

В любом живом организме выполняются сложные биоэлектрические процессы. Например, в молекуле ДНК при закручивании или раскручивании ее структурной спирали направление таких взаимодействий должно идти по геодезическому углу. Под таким же углом работает тутовый шелкопряд при наматывании шелковой нити на основу.

В динамике конфармации ДНК большое значение имеют так же протон-электронные взаимодействия между подсистемами этой молекулы. Возникающие при этом гравитоны несут в себе энергетическую и генетическую информацию от каждой  молекулы ДНК.

В виду специфичности и слабой интенсивности такого поля, оно не регистрируется обычными приборами, но может регистрироваться родственными системами, а так же такими системами, которые могут перестраиваться в резонанс с исходной. Очевидно, в этом и находится  главная причина известных эффектов так называемой телепатии. Но это процесс биогравитации. В неживой природе в некоторых случаев, например, в космологии наряду с обычным взаимодействием может в небольшой степени проявляться взаимодействие по принципу открытых систем. Возможно, с наличием такого взаимодействия как-то связано известное по ОТО «искривление пространства».

Выводы

1. Используя условие стационарного состояния в корпускулярно-волновых взаимодействиях и в рамках нерелятивисткой механики проведен анализ механизма процессов тяготения.
2. Получено уравнение функциональной зависимости постоянной тяготения от электрической постоянной.
3. Предполагается, что тяготение есть волновой вклад от массы заряженных частиц при движении их в поле центральных сил. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Иваненко Д. Д. Гравитация / Иваненко Д. Д., Сарданашвили Г. А. М.: Едиториал УРСС, 2004, ISBN 5-354-00538-8
2. [Электронный ресурс] – URL: https://ru.wikipedia.org/w/index.php?title=Классическая_теория_тяготения_ Ньютона&oldid=101565038 (дата обращения: 13.11.19)
3. Физический энциклопедический словарь. М.: «Большая Российская Энциклопедия», т.3, 1992, 672 с.
4. Киттель Ч. Курс физики т.1 Механика / Киттель Ч., Найт У. Рудерман М. «Наука», 1971, 479с.
5. Физическая Энциклопедия, М.: «Советская Энциклопедия», т.1, 1988, 704 с.
6. Физический энциклопедический словарь. М.: «Советская Энциклопедия», т.5, 1966, 576 с.
7. Approaches to Quantum Gravity. Toward a New Understanding of Space, Time and Matter/ Ed. by D. Oriti. — Cambridge: Cambridge University Press, 2009. — xix + 583 p. — ISBN 978-0-521-86045-1.
8. Korablev G.А. On problematic issues of physical chemistry / Korablev G.А., JMEST, v6, 2019, pp10320-10324
9. Угаров А. Специальная теория относительности / Угаров А. . М.: «Наука», 1977, 385с.
10. Пидгайный Ю.М. Механика полимеров / Пидгайный Ю.М., Морозова В.М., Дудко В.А.– 1967.– № 6 – С. 1096-1104.
11. Кодолов В.И. Полимерные композиции и технология изготовления из них двигателей летательных аппаратов. Ижевский механический институт / Кодолов В.И. 1992, – 200 с.

Список литературы на английском языке / References in English

1. Ivanenko D. D. Gravitaciya [Gravity] / Ivanenko D. D., Sardanashvili G. A. : URSS editorial, 2004, ISBN 5-354-00538-8 [in Russian]
2. [Electronic resource] – URL: https: //ru.wikipedia.org/w/index.php? Title = Classical_the_ gravitation theory_Newton & oldid = 101565038 (accessed: 13.11.19) [in Russian]
3. Fizicheskij enciklopedicheskij slovar' [The physical encyclopedic dictionary]. M .: "Big Russian Encyclopedia", Vol. 3, 1992, 672 p. [in Russian]
4. Kittel H. Kurs fiziki t.1 Mekhanika [Physics course vol. 1 Mechanics] / Kittel H., Knight W., Ruderman M. Science, 1971, 479 pp. [in Russian]
5. Fizicheskaya Enciklopediya [Physical Encyclopedia], M .: “Soviet Encyclopedia”, v.1, 1988, 704 p. [in Russian]
6. Fizicheskij enciklopedicheskij slovar' [Physical encyclopedic dictionary]. M .: "Soviet Encyclopedia", v.5, 1966, 576 p. [in Russian]
7. Approaches to Quantum Gravity. Toward a New Understanding of Space, Time and Matter [Approaches to Quantum Gravity. Toward a New Understanding of Space, Time and Matter] / Ed. by D. Oriti. - Cambridge: Cambridge University Press, 2009 .-- xix + 583 p. - ISBN 978-0-521-86045-1. [in Russian]
8. Korablev G.A. On problematic issues of physical chemistry [On problematic issues of physical chemistry] / Korablev G.A., jmest, v6, 2019, pp10320-10324
9. Ugarov A. Special'naya teoriya otnositel'nosti [Special Theory of Relativity] / Ugarov A. . M .: "Science", 1977, 385p. [in Russian]
10. Pidgainy Yu.M. Mekhanika polimerov [The mechanics of polymers] / Pidgainy Yu.M., Morozova V.M., Dudko V.A. - 1967.– No. 6 - P. 1096-1104. [in Russian]
11. Kodolov V.I. Polimernye kompozicii i tekhnologiya izgotovleniya iz nih dvigatelej letatel'nyh apparatov. Izhevskij mekhanicheskij institute [Polymer compositions and manufacturing technology of aircraft engines from them] / Kodolov V.I. Izhevsk Mechanical Institute, 1992, - 200 p. [in Russian]