СТАТИСТИКА МОДОВОГО СОСТАВА ВИХРЕВЫХ МАТРИЧНЫХ ПУЧКОВ ПРИ РАСПРОСТРАНЕНИИ В АТМОСФЕРЕ

СТАТИСТИКА МОДОВОГО СОСТАВА ВИХРЕВЫХ МАТРИЧНЫХ ПУЧКОВ ПРИ РАСПРОСТРАНЕНИИ В АТМОСФЕРЕ

Научная статья Аксенов В.П.¹, Дудоров В.В.², Колосов В.В.³, Филимонов Г.А.^4, * ² ORCID: 0000-0002-9660-5199; ⁴ ORCID: 0000-0003-4358-423X; ^{1, 2, 3, 4} Институт оптики атмосферы им. В.Е. Зуева Сибирского отделения РАН, Томск, Россия * Корреспондирующий автор (fga[at]iao.ru)

Аннотация В работе анализируется модовый состав излучения вихревых матричных лазерных пучков, синтезированных матрицей когерентных оптоволоконных излучателей. На основе численного моделирования анализируется перекачка энергии между вихревыми азимутальными модами излучения при распространении в свободном пространстве и турбулентной атмосфере. Показано, что в дальней зоне большая часть энергии излучения перекачивается в основную моду, определяемую топологическим зарядом синтезированного пучка. При наличии турбулентности статистические характеристики модового состава синтезированного вихревого матричного пучка аналогичны характеристикам Лагерр-Гауссова пучка. Ключевые слова: вихревые лазерные пучки, массив когерентных излучателей, турбулентная атмосфера.

STATISTICS OF MODE CONTENT OF VORTEX MATRIX BEAMS DURING DISTRIBUTION IN ATMOSPHERE

Research article

Aksenov V.P.¹, Dudorov V.V.², Kolosov V.V.³, Filimonov G.A.^4, * ² ORCID: 0000-0002-9660-5199; ⁴ ORCID: 0000-0003-4358-423X; ^{1, 2, 3, 4} V.E. Zuev Institute of Atmospheric Optics, Siberian Branch of the Russian Academy of Sciences, Tomsk, Russia * Corresponding author (fga[at]iao.ru)

Abstract This paper analyzes the mode composition of the radiation from vortex matrix laser beams synthesized by a coherent fiber-optic emitter matrix. The energy transfer between the vortex azimuthal radiation modes during propagation in free space and turbulent atmosphere is analyzed on the basis of numerical simulation. It is shown that most of the radiation energy is pumped into the main mode in the far-field zone, which is determined by the topological charge of the synthesized beam. Statistical characteristics of the mode composition of the synthesized vortex matrix beam are similar to those of the Laguerre-Gaussian beam in case of turbulence. Keywords: vortex laser beams, array of coherent emitters, turbulent atmosphere.

Последнее время внимание исследователей привлекает технология сложения излучения массива когерентных излучателей [1-6]. По своим характеристикам массив таких излучателей может превосходить системы на основе традиционных телескопов [7]. В задачах оптической связи важной является возможность генерации вихревых лазерных пучков [8], которые сохраняют орбитальный угловой момент (ОУМ) [9-13] при распростренении излучения от передатчика к приемнику [14]. Синтез вихревых пучков на основе сложения излучения массива когерентных излучателей [15] характеризуется особенностью при определении их ОУМ [16]. При этом общий ОУМ пучка в силу закона сохранения момента равен нулю, а ОУМ, определяемый в пределах ограниченной апертуры в дальней зоне, совпадает с топологическим зарядом синтезированного матричного вихревого пучка. Очевидно, что из-за интерференции излучения субапертур по мере распространения таких пучков в свободном пространстве их модовый состав будет меняться. Кроме того, наличие турбулентных неоднородностей на трассе распространения будет вызывать искажения и перераспределять энергию излучения между модами. В связи с этим в настоящей работе выполнено исследование динамики и флуктуаций азимутального модового состава вихревых синтезированных матричных пучков при их распространении в турбулентной атмосфере.

Начальное поле синтезированного матричного вихревого пучка представим в виде суммы полей на N_a субапертурах матрицы волоконных лазеров в следующем виде:

   

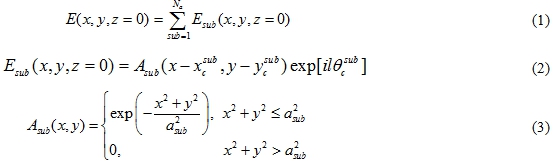
где  полярные координаты, l – значение топологического заряда,  - координаты центра, a_sub - радиус субапертуры. При этом в случае гексагональной упаковки субпучков отсутствует центральный субпучок с координатами x=0, y=0. Кроме этого при формировании синтезированного пучка из нескольких колец субпучков (N_a = 18, 36, 60 и т.д.) также могут отсутствовать внутренние кольца. Анализ особенностей генерации и распространения таких пучков в турбулентной атмосфере выполнен на основе сравнения с полем Лагерр-Гауссова пучка [17] радиуса a:

Начальные распределения амплитуды и фазы поля Лагерр-Гауссового пучка для топологического заряда l = 1 представлены на рис.1 (слева). Справа представлены несколько аналогичных распределений для синтезированных матричных пучков с различным количеством субапертур.

Рис. 1 – Амплитуда (верхний ряд) и фаза (нижний) Лагерр-Гауссова и синтезированного вихревого пучка при разном количестве субапертур N_a. l = 1

Примечание: здесь и далее шкала яркости для амплитуды поля от 0 то максимального значения, для фазы поля от 0 до 2p.

Видно, что чем больше количество субапертур, составляющих синтезированный вихревой пучок фиксированного радиуса, тем меньше радиус отдельной субапертуры. Распространение пучков в атмосфере будем рассчитывать, используя параболическое уравнение

где, – оператор Лапласа, n₁ (x,y,z) – возмущение показателя преломления воздуха относительно своего равновесного значения - волновое число. Возмущение показателя преломления n₁ (x,y,z) будем считать однородным, изотропным и Колмогоровским [18], [19]. Алгоритм численного решения (6) на основе метода расщепления по физическим факторам [20] впервые был описан в работе [21], где было введено понятие тонкого фазового экрана, представляющего собой модель турбулентного слоя атмосферы. Долгое время в численных экспериментах использовались ограниченные (конечные) фазовые экраны. В [22] предложена численная модель бесконечного турбулентного фазового экрана для моделирования продолжительных экспериментов. Параллельная реализация численных алгоритмов решения (6) описана в [23]. В [24] показана возможность использования в моделировании экспериментальных данных измерений параметров атмосферы. В [25], [26] предлагаются подходы, учитывающие регулярную рефракцию, связанную с нелинейной зависимостью показателя преломления от высоты, а также случайные рефракционные эффекты на крупномасштабных турбулентных неоднородностях, которые могут приводить к значительным вертикальным и горизонтальным отклонениям траектории распростренения лазерных пучков от прямой линии. Рассмотрим распространение синтезированного матричного вихревого пучка в вакууме Расчитанные распределения амплитуды и фазы поля на различной дистанции от начальной плоскости представлены на рис. 2. Очевидно, что неоднородная интерференционная структура поля на начальном участке трассы распространения будет вносить искажения в значение ОУМ.

Рис. 2 – Динамика амплитуды и фазы поля синтезированного вихревого пучка (l = 1) при распространении в вакууме.

Оценку влияния неоднородной структуры поля синтезированного пучка на его характеристики можно выполнить на основе разложении поля по азимутальным модам вихревого пучка следующего вида:

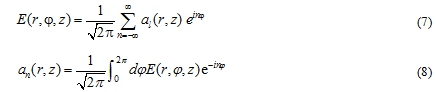
Далее для идентификации топологического заряда синтезированного вихревого пучка необходимо вычислить долю энергии, соответствующую модам разного порядка n.

На рис. 3 представлена динамика энергии мод P_n синтезированного вихревого пучка с топологическим зарядом l = 1, сфокусированного на дистанцию z = 0.1ka² (а), 0.2 (б), 0.5 (в) в вакууме.

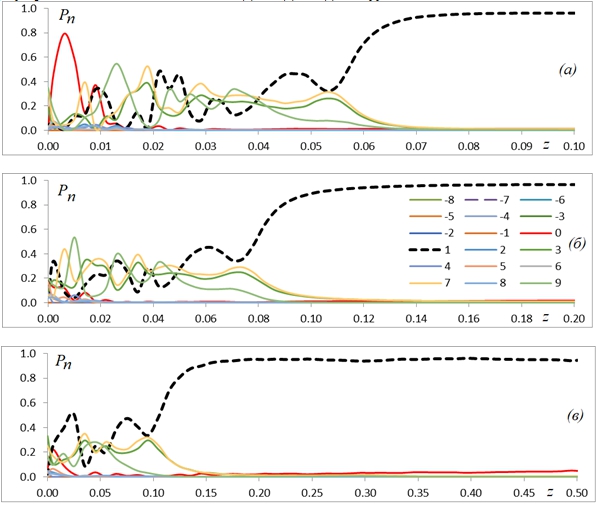
Рис. 3 – Динамика энергии мод P_n синтезированного вихревого пучка с топологическим зарядом l = 1, сфокусированного на дистанцию z = 0.1ka² (а), 0.2 (б), 0.5 (в) в вакууме Примечание: Синтезированный вихревой пучок аналогичен представленному на рис.2.

Видно, что в отличие от непрерывного вихревого пучка при распространении синтезированного пучка на начальном участке трассы распространения происходит перекачка энергии между модами, соответствующими разным значениям n. При этом по мере распространения энергия моды n = 1, порядок которой равен заданному топологическому заряду l = 1, возрастает и испытывает насыщение на уровне 95%. Выход на уровень насыщения соответствует дистанциям распространения более 0.1 длины дифракции для коллимированных пучков и существенно сокращается при фокусировке пучков.

Наличие турбулентности на трассе распространения изменяет модовый состав пучка. На рисунке 4 представлены зависимости среднего значения и стандартного отклонения энергии моды от дистанции распространения.

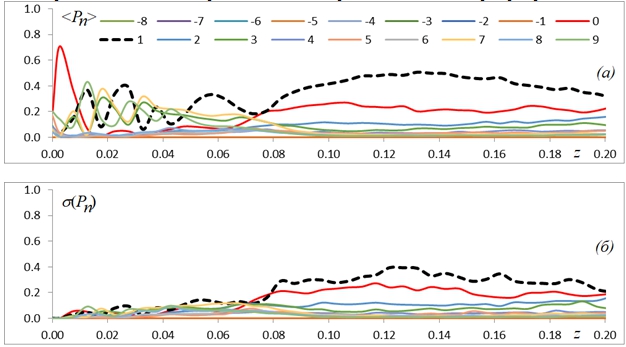
Рис. 4 – Зависимость среднего значения (а) и стандартного отклонения (б) энергии моды P_n при распространении синтезированного матричного пучка в турбулентной атмосфере на дистанцию z = 0.2ka². l = 1, D/r₀ = 4

Видно, что характер данных кривых для дистанций, соответствующих выходу на насыщение энергии синтезируемой моды (см. рис.3), аналогичен зависимостям, полученным для непрерывного Лагерр-Гауссова пучка. Уровень насыщения энергии синтезируемой моды в турбулентности становится ниже, чем уровень насыщения для вакуума за счет случайной перекачки энергии из основной моды в соседние. Чем больше соотношение D/r₀ , характеризующее силу турбулентности, тем меньше становится различие между уровнями энергии различных мод, независимо от того, какая из них является главной (синтезированной).

Финансирование Статья подготовлена по результатам работы, выполненной при финансовой поддержке Российского научного фонда (проект №18-19-00437).	Funding The article was prepared based on the results of the work carried out with the financial support of the Russian Science Foundation (project No. 18-19-00437).
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Filimonov G. A. Performance analysis of a coherent tiled fiber-array beam director with near-field phase locking and programmable control of tip/tilt and piston phases / Filimonov G. A., Vorontsov M. A., Lachinova S. L. // Proc. SPIE 8971, Free-Space Laser Communication and Atmospheric Propagation XXVI. – 2014. – 897109.
2. Banakh V. A. Numerical simulation of propagation of laser beams formed by multielement apertures in a turbulent atmosphere under thermal blooming / Banakh V. A., Falits A. V. // Atmospheric and oceanic optics. – 2013. – V. 26. – № 6. – P. 455–465.
3. Weyrauch T. Experimental demonstration of coherent beam combining over a 7 km propagation path / Weyrauch T., Vorontsov M. A., Carhart G. W and others // Opt. Lett. – 2011. – V. 36. – № 22. – P. 4455–4457.
4. Воронов В. И. Поле в дальней зоне многоволоконного излучателя при угловой разъюстировке первичного источника / Воронов, В. И., Нурамов, Ф. Н., Аль, Т. И. // Нелинейный мир. – 2017. – T. 15. – № 1. – С. 54–57.
5. Hyde, M. W. Behavior of tiled-aperture arrays fed by vector partially coherent sources / Hyde, M. W., & Spencer, M. F. // Applied optics. – 2018. – V. 57. – № 22. – P. 6403–6409.
6. Антипов О. Л. Адаптивная коррекция искажений, возникающих в многоканальной оптической системе / Антипов О. Л., Канев Ф. Ю., Цыро Е.И и др. // Оптика атмосферы и океана. – 2012. – Т. 25. – № 9. – С. 801–809.
7. Vorontsov M. A. Comparative efficiency analysis of fiber-array and conventional beam director systems in volume turbulence / Vorontsov M. A., Filimonov G. A., Ovchinnikov V. and others // Appl. Opt. – 2016. – V. 55. – P. 4170–4185.
8. Aksenov V. P. Orbital angular momentum of laser beam in the turbulent medium: asymptotic estimates and numerical simulation / Aksenov V.P., Kolosov V.V., Filimonov G.A. and Pogutsa Ch.E. // Proc. of SPIE. – 2015. – V. 9680. P. 96800P-1-6.
9. Jackson J. D. Classical Electrodynamics / J. D. Jackson. – New York: Wiley, 1999.
10. Allen L. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes / Allen L., Beijersbergen M.W., Spreeuw R.J.C. and others // Phys. Rev. A. – 1992. – V. 45. – P. 8185
11. Bekshaev A. Paraxial Light Beams with Angular Momentum / Bekshaev A, Soskin M. and Vasnetsov M.. — New York: Nova Science, 2008.
12. Yao A. M. Orbital angular momentum: origins, behavior and applications / Yao A. M. and Padgett M. J. // Adv. Opt. Photon. – 2011. – V. 3. – P. 161–204
13. Soskin, M. Singular optics and topological photonics / Soskin, M., Boriskina, S.V., Chong, Y., Dennis, M.R., & Desyatnikov, A. // Journal of Optics. – 2016. – V. 19. – № 1. – P. 010401.
14. Aksenov V. P. Orbital angular momentum of a laser beam in a turbulent medium: preservation of the average value and variance of fluctuations / Aksenov V. P., Kolosov V. V., Filimonov G. A. and others // Journal of Optics. – 2016. – V. 18. – № 5. – P. 054013.
15. Аксенов В. П. Особенности вихревых пучков, сформированных матрицей волоконных лазеров, и их распространение в турбулентной атмосфере / Аксенов В. П., Дудоров, В. В., Колосов В. В. // Квантовая электроника. – 2016. – Т. 46. – № 8. – С. 726–732.
16. Aksenov V. P. Vortex beams with zero orbital angular momentum and non-zero topological charge / Aksenov V. P., Dudorov V. V., Filimonov G. A. and others // J. Opt. Laser Technol. – 2018. – V. 104. – P. 159–163.
17. Фалиц А. В. Блуждание и флуктуации интенсивности фокусированного Лагерр–Гауссова пучка в турбулентной атмосфере / Фалиц А. В. // Оптика атмосферы и океана. – 2015. – Т. 28. – № 9. – С. 763-771.
18. Tatarskii V. I. Wave Propagation in a Turbulent Medium. — New York: McGraw-Hill, 1961.
19. Kolmogorov A. N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers / Kolmogorov A. N. // Dokl. Akad. Nauk SSSR. – 1941. – T. 30. – C. 299–303.
20. Марчук Г. И. Методы расщепления / Г. И. Марчук. — М.: Наука, 1980.
21. Fleck J. A. Time Dependent Propagation of High Energy Laser Beams through the Atmosphere / Fleck J. A., Morris J.R., Feit M.D. // Appl. Phys. A. – 1976. – V. 10. – P. 129–160.
22. Дудоров В. В. Алгоритм формирования бесконечных турбулентных экранов для моделирования долговременных лазерных экспериментов в атмосфере / Дудоров В.В., Колосов В.В., Филимонов Г.А. // Известия Томского политехнического университета. Инжиниринг георесурсов. – 2006. – Т. 309. – № 8. – С. 85–89.
23. Коняев П. А. Численное моделирование распространения оптических волн с использованием технологий параллельного программирования / Коняев П. А., Тартаковский Е. А., Филимонов Г. А. // Оптика атмосферы и океана. – 2011. – Т. 24. – № 5. – С. 359–365.
24. Kulikov V. A. Simulation of laser beam propagation based on mesoscale modeling of optical turbulence and refractivity / Kulikov V.A., Basu S., Vorontsov M.A. // OSA Conference: Propagation Through and Characterization of Atmospheric and Oceanic Phenomena, PTh3D-3, 26–29 June 2017, San-Francisco, USA, 2017
25. Kolosov V. V. Accounting for the effect of large-scale atmospheric inhomogeneities in problems of laser radiation propagation along long high-altitude paths / Kolosov, V.V., Dudorov, V.V., Filimonov, G.A., Panina, A.S., Vorontsov, M.A. // Atmos Ocean Opt. – 2014. – V. 27. – № 2. – P. 123–129.
26. Kulikov V. A. Analysis of the joint impact of atmospheric turbulence and refractivity on laser beam propagation / Kulikov, V. A., Vorontsov, M. A. // Opt. Express. – 2017. – V. 25. – P. 28524–28535.