ОБ ОЦЕНКАХ ОБЪЕМА ГОРНОГО ОЛЕДЕНЕНИЯ И ВРЕМЕНИИ ОТКЛИКА НА КЛИМАТИЧЕСКИЕ ИЗМЕНЕНИЯ

ОБ ОЦЕНКАХ ОБЪЕМА ГОРНОГО ОЛЕДЕНЕНИЯ И ВРЕМЕНИИ ОТКЛИКА НА КЛИМАТИЧЕСКИЕ ИЗМЕНЕНИЯ

Научная статья

Рыбак Е.А.^1, *, Рыбак О.О.²

¹ ORCID: 0000-0003-0920-4176;

² ORCID: 0000-0003-3923-7163;

^{1, 2} Сочинский научно-исследовательский центр РАН, Сочи, Россия;

^{1, 2} Филиал Института природно-технических систем, Сочи, Россия

* Корреспондирующий автор (elena.rybak[at]gmail.com)

Аннотация

В настоящее время в мире насчитывается более 200 тысяч горных ледников. Регулярные наблюдения за поверхностным балансом массы и изменениями геометрии охватывают лишь малую их часть. В связи с этим, для решения задач реконструкции оледенения и его прогноза целесообразно применять метод математического моделирования различных аспектов их динамики. В настоящей статье рассмотрены вопросы приложения математического моделирования для расчета двух важных характеристик горного оледенения – связи между площадью ледника и его объемом и времени отклика на внешнее воздействие. Показано, что в небольших ансамблях численных экспериментов, возможно, получить оценки этих характеристик и установить их связь с климатическими переменными.

Ключевые слова: горный ледник, объем ледника, климатические изменения, время отклика,математическая модель.

ON EVALUATION OF MOUNTAIN GLACIATION AMOUNT AND TIME OF RESPONSE TO CLIMATIC CHANGES

Research article

Rybak E.A.^1, *, Rybak O.O.²

ORCID: 0000-0003-0920-4176;

ORCID: 0000-0003-3923-7163;

^{1, 2} Sochi Research Center of the Russian Academy of Sciences, Sochi, Russia;

^{1, 2.}Branch of the Institute of Natural-Technical Systems, Sochi, Russia

*Corresponding author (elena.rybak[at]gmail.com)

Abstract

Currently, there are more than 200 thousand mountain glaciers in the world. Regular observations of the surface mass balance and geometry changes cover only a small part of them. Taking this into account, in order to solve the problems of reconstruction of glaciation and its forecast, it is advisable to apply the mathematical modeling method for various aspects of their dynamics. This article discusses the application of mathematical modeling to calculate two important characteristics of mountain glaciation – the relationship between the area of the glacier, it’s amount and the response time to external influences. It is shown that in small ensembles of numerical experiments, it is possible to obtain estimates of these characteristics and establish their relationship with climate variables.

Keywords: mountain glacier, glacier volume, climate change, response time, mathematical model.

Введение

Задачи определения времени отклика горного ледника на внешнее воздействие и определения соотношения между площадью и объемом оледенения являются взаимосвязанными, и имеют как чисто академические, так и практические приложения. К первым можно отнести, в частности, возможность верификации и валидации численных моделей эволюции ледников, ко вторым – определения водно-ледниковых ресурсов. Дело в том, что мониторинг площади горного оледенения возможно осуществлять дистанционными методами (спутниковыми или с помощью беспилотных летательных аппаратов). Однако информация о площади ледников сама по себе не дает представления об объеме аккумулированного льда. Обычно при оценке изученности горных ледников ссылаются на работу [1], в которой приводятся следующие цифры: в конце 20-го века в мире насчитывалось более 200 тысяч горных ледников, а толщина и объем льда были известны не более чем для 0,1% из этого количества. Между тем, оценка текущих и будущих значений объема горного оледенения в условиях меняющегося климата актуальна для расчета ледникового стока, который вносит существенный вклад в общий речной сток на обширных горных и предгорных территориях. В связи с тем, что численное моделирование в принципе не может охватить даже малую часть ледников планеты, неизбежно применение разного рода экстраполяционных методов, основанных, в том числе, и на соотношении между площадью и объемом ледников (Volume-Area scaling или VAS). Поскольку расчет объема индивидуального ледника по его площади может содержать значительную (до 50%) ошибку [2], применять эту процедуру рекомендуется к группе ледников [1], тогда ошибка снижается до 25% [2]. Использование процедуры VAS может быть очень полезным для оценки результатов численного моделирования, особенно, если речь идет об ансамбле численных экспериментов. Из-за некоторой инерции ледники редко находятся в равновесии с текущим климатом (если его рассматривать, как осредненные за два-три десятилетия значения приземной температуры воздуха, сумм осадков, радиации и т.д.). Оценка времени отклика ледника на внешнее воздействие необходимо для того, чтобы по возможности наиболее корректно разделить его реакцию на прошлые и текущие климатические изменения, и, таким образом, для обоснованного прогноза эволюции.

В настоящей работе нами использованы методы математического моделирования для исследования зависимости объема ледника от его площади на примере ледника Сары-Тор (Внутренний Тянь-Шань) и времени отклика ледника Джанкуат (Центральный Кавказ) на внешнее климатическое воздействие. При выборе ледников мы руководствовались степенью их изученности и доступностью максимального объема исходных данных по геометрии, поверхностного баланса массы и т.д.

Аналитические методы VAS

Вокруг применения методов, аналитически связывающих объем горного ледника с его площадью, дискуссии продолжаются не один год. Первоначально, разумеется, в основание метода VAS были положены данные наблюдений. Было замечено, что площади ледника соответствует вполне определенный объем, что может быть использовано для расчета водно-ледниковых ресурсов. Исходя из предположения о том, что поперечный профиль долинного ледника имеет параболическую форму, Ерасов [3] предположил, что его объем должен быть пропорционален площади:

  (1)

где γ=1,5, а коэффициент A связан с морфометрическими и морфологическими характеристиками конкретного ледника. В многочисленных последующих работах оба коэффициента рассматривались как эмпирические. Проанализировав данные об объеме и площади около полутора сотен горных ледников по всему миру и на основании некоторых теоретических выкладок, Бар (Bahr) с соавторами подтвердили, что характерный объем и характерная площадь ледников долинного типа связаны соотношением (1) [1]. Заметим, однако, что в их трактовке речь идет именно о характерных величинах, и о применимости выражения (1), по меньшей мере, к группе ледников, а не к единственному леднику. Более того авторы [4] категорически настаивают на универсальности значения константы γ=1,375, оставляя возможность варьировать при подборе аппроксимирующего выражения лишь множитель A. Тем не менее, это основополагающее положение явно или неявно оспаривается многими исследователями. В частности, в работе [2] было осуществлено разбиение почти трехсот равновесных модельных конфигураций ледников на группы по площади, форме и крутизне склонов. Это позволило детализировать соотношение между площадью и объемом. Исследование диапазонов  дало глобальные средние значения A=0,027 и γ=1,458.

Математическая модель

Используемая в настоящей работе математическая модель, ее архитектура, система уравнений и численные методы решения были подробно рассмотрены в работах [5], [6], [7], [8]. Структура модели, описанная в [5], в последующем не подвергалась существенным изменениям. Уравнения течения льда основаны на так называемом приближении «неполного второго порядка» [9] – компромиссе между решением полной системы уравнений Стокса, включающей все виды напряжений, и «приближением мелкого льда», в котором учитываются только напряжения сдвига в вертикальной плоскости. Алгоритмы масс-балансового блока основаны на подсчете энергии, доступной для таяния в бесконечно тонком поверхностном слое [10], без учета теплообмена с нижележащими слоями. Теплообмен заморененных областей (покрытых слоем поверхностной морены – моренным чехлом) с атмосферой и с подстилающей поверхностью льда рассчитывается путем решения одномерного уравнения теплопроводности [6].

Исходные данные и постановка численных экспериментов

Для исследования были выбраны два ледника приблизительно одной площади – несколько менее 3 км² (рис. 1). VAS-процедура была выполнена в ходе прогностических численных экспериментов по моделированию эволюции ледника Сары-Тор, по исследованию времени отклика – в аналогичных экспериментах с ледником Джанкуат.

Ледник Сары-Тор (Внутренний Тянь-Шань). Поле толщины льда было реконструировано по материалам радиозондирования, выполненного в мае 2013 г., контуры ледника были получены в результате дешифровки космического снимка 2012 г. [11]. Данные расчетов были приведены к узлам регулярной пространственной сетки с шагом 25 м. К этим же узлам было приведено поле высоты поверхности, основанное на цифровой модели рельефа ASTER GDEM V2 (gdem.ersdac.jspacesystems.or.jp). В качестве климатического форсинга были использованы данные по среднесуточной температуре воздуха и суточным суммам осадков на метеостанции Тянь-Шань-Кумтор, расположенной в нескольких километрах от ледника.

Было проведено в общей сложности десять численных экспериментов, в которых градиент температуры менялся в пределах 0-4°С / 100 лет с шагом 1°С для двух вариантов реологии льда, которые в итоге выражались в двух вариантах поля скорости течения (поскольку непосредственные измерения скорости отсутствуют).

 

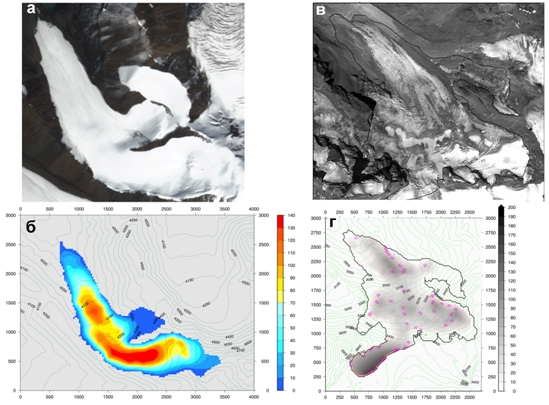
Рис. 1 – Горные ледники, исследуемые в настоящей работе: Сары-Тор (а, б) и Джанкуат (в, г); спутниковые снимки (а, в), геометрия, высота, м над уровнем моря, и толщина льда, м (б, г); Ледник Джанкуат (Центральный Кавказ)

 

Поле было построено на основе данных радиозондирования [12], за исключением области в верхней части ледника – труднодоступного Джантуганского фирнового плато, где оценка толщины льда была выполнена косвенными методами [13]. Толщина моренного слоя и распределение его по поверхности ледника соответствуют состоянию на 2010 г. [14]. В качестве климатического форсинга использовались ряды срочных наблюдений за приземной температурой воздуха на сетевой метеостанции Терскол и осадков на станции Местиа. Температура воздуха приводилась методом линейной регрессии к высоте 3100 м [7], на которой в течение нескольких летних сезонов функционировала автоматическая метеостанция. Пересчет рядов осадков в ряды зимнего баланса массы производился с учетом особенностей циркуляции атмосферы, вертикального градиента осадков и лавинного питания [7].

Было выполнено одиннадцать численных экспериментов, длительностью 150 модельных лет (табл. 1) [15].

 

Таблица 1 – Перечень численных экспериментов и значения ключевых факторов форсинга (МЧ – включение моренного чехла, ∆T – скачок температуры, ∆P – фактор изменения сумм осадков)

№ эксп.	1	2	3	4	5	6	7	8	9	10	11
МЧ	Нет	Да	Да	Да	Да	Да	Да	Да	Да	Да	Да
∆T	0	0	1	2	3	0	0	3	3	3	3
∆P	1	1	1	1	1	0,8	0,5	1,2	1,5	0,8	0,5

 

Эксперименты №1 и №2 были выполнены для условного современного климата. В эксперименте №1 из расчетов был исключен теплообмен моренного чехла с атмосферой и нижележащим слоем льда. В экспериментах №№3-5 и №№8-11 значения температуры воздуха в начале каждого эксперимента увеличивались на ∆T=1-3 °С. Изменение сумм осадков имитировалось умножением исходных сумм на значения, указанные в табл. 1. В экспериментах №№8-11 к увеличенным суммам осадков добавлен рост температуры воздуха.

Результаты и обсуждение

Связь между площадью и объемом (ледник Сыры-Тор). В численных экспериментах длительностью 100 модельных лет было получено десять конфигураций ледника. Данные по площади и объему, соответствующие этим конфигурациям, а также наблюденная площадь [11] и рассчитанный по данным наблюдений объем были использованы для построения аппроксимирующей функции вида (1). Было установлено, что для различных конфигураций ледника Сары-Тор (их можно считать своеобразным ансамблем), оптимальным оказался набор A=0,030 и γ=1,669 (рис. 2). Заметим, что значение коэффициента γ, превышает заявленное в качестве универсального значение γ=1,375 [4], и ближе к экспериментально установленному γ=1,458 [2]. Вполне вероятно, что подход к VAS-процедуре в работе [2], которая предусматривает разбиение ледников на несколько классов со своим набором параметров для каждого класса, и которая неявным образом учитывает различия в динамике ледников, более обоснована, нежели подход, реализуемый в [4], и основанный на достаточно сложных теоретических выкладках. Для сравнения с нашими результатами на рис. 2 была добавлена кривая, построенная с использованием значений пары параметров A=0,035 и γ=1,375. Очевидно, что кривая неплохо аппроксимирует модельные конфигурации при выпадающей наблюденной конфигурации (зеленый квадрат на рис. 2). В случае подбора значения A так, чтобы аппроксимирующая кривая проходила через точку, соответствующую наблюденной конфигурации, аппроксимировать модельные конфигурации не удается.

Время отклика на внешнее воздействие (ледник Джанкуат). По определению время отклика ледника на внешнее воздействие – это время, которое требуется леднику для перехода из одного равновесного состояния в другое. Поскольку в реальном мире ледник практически никогда не находится в равновесном состоянии с климатом, эта характеристика представляется несколько абстрактной. Тем не менее, время отклика – полезный показатель, который помогает отделить текущие изменения характеристик ледника от изменений, вызванных предшествующими климатическими изменениями.

 

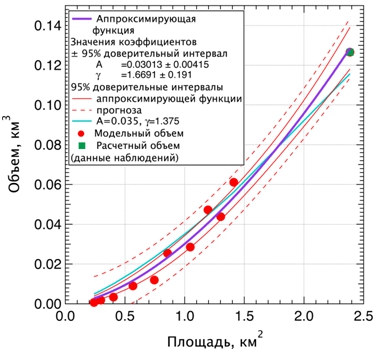
Рис. 2 – Площадь, км², и объем, км³ ледника Сары-Тор в численных экспериментах (красные кружки) и рассчитанные по данным наблюдений (зеленый квадрат), оптимальная аппроксимирующая степенная функция (фиолетовая кривая) и 95% – доверительные интервалы, теоретическая аппроксимирующая степенная функция (голубая кривая)

 

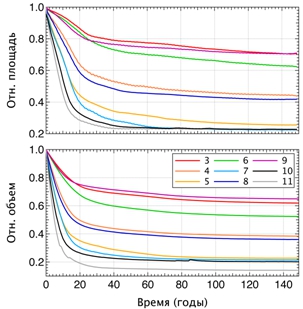
Достаточно полный обзор аналитических методов дан в [16]. Мы остановимся на обсуждении экспериментальных результатов, которые были получены в экспериментах 3-11 (табл. 1). Модельные конфигурации детально обсуждаются в [15], мы же в настоящей работе обсуждаем только время отклика. Для сопоставимости результатов площадь и объем ледника, рассчитанные в этих экспериментах, были нормированы на соответствующие величины, рассчитанные в эксперименте №2 с нулевыми значениями форсинга (рис. 3).

Рис. 3 – Изменения нормированных (относительных) площадей (вверху) и объемов (внизу) ледника Джанкуат в ходе 150-летних численных экспериментов

 

Очевидно, что максимальные изменения происходят в течение первых 20 модельных лет после вывода ледника из равновесия. Для более детального анализа времени отклика воспользуемся экспоненциальным масштабом τ, то есть временным промежутком, в течение которого ледник теряет долю объема, равную  от первоначального [16]. Расчеты показывают, что прослеживается тенденция уменьшения времени отклика с увеличением климатического форсинга и, соответственно, уменьшением конечного объема (табл. 2).

 

Таблица 2 – Результаты численного моделирования эволюции ледника Сары-Тор (V_end – равновесный нормированный (безразмерный) объем в конце численных экспериментов, τ – время отклика, годы)

№ эксп.	3	4	5	6	7	8	9	10	11
Vend	0,619	0,384	0,223	0,524	0,214	0,360	0,649	0,202	0,141
t	20	13	11	19	16	12	16	8	7

  Заключительные замечания

В статье были рассмотрены две важные характеристики горного оледенения – связь между площадью ледника и его объемом и характерное время отклика на изменение климатических переменных. Показано, что при недостатке регулярных наблюдений указанные характеристики могут быть реконструированы методом математического моделирования в небольших ансамблях численных экспериментов. В дальнейшем предполагается провести сравнение полученных результатов с аналогичными исследованиями.

Благодарности Авторы выражают благодарность рецензенту Гайдуковой Екатерине Владимировне, чьи замечания и советы способствовали улучшению текста статьи.	Acknowledgement The authors are grateful to the reviewer Ekaterina Gaidukova, whose comments and advice contributed to the improvement of the article.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Bahr D. B. The physical basis of glacier volume-area scaling / D. B. Bahr, M. F. Meier, S. D. Peckham // Journal of Geophysical Research. – 1997. – Vol. 102. – P. 20355-20362.
2. Adhikari S. Glacier volume-area relation for high-order mechanic and transient glacier states / S. Adhikari, S. J. Marshall // Geophysical Research Letters. - 2012. – Vol. 39. – L16505. DOI:10.1029/2012GL052712
3. Ерасов Н. В. Метод определения объема горных ледников / Н. В. Ерасов // Материалы гляциологических исследований. – 1968. – Вып. 14. – C. 307-308.
4. Bahr D. B. A review of volume-area scaling of glaciers / D.B. Bahr, W.T. Pfeffer, G. Kaser // Reviews of Geophysics. – 2015. – Vol. 53. – P. 95-140. DOI:10.1002/2014RG000470.
5. Рыбак О. О. Калибровка математической модели динамики ледника Марух, Западный Кавказ / О.О. Рыбак, Е.А. Рыбак, С.С. Кутузов и др. // Лед и снег. – 2015. – Т. 55. – № 2. – С. 9-20. DOI: https://doi.org/10.15356/2076-6734-2015-2-9-20
6. Рыбак О. О. Модельные расчеты подморенного таяния на леднике Джанкуат / О. О. Рыбак, Е. А. Рыбак, И. А. Корнева // Системы контроля окружающей среды. – 2018. – Вып. 12 (32). – С. 86-92.
7. Rybak O. O. Model-based calculations of surface mass balance of mountain glaciers for the purpose of water consumption planning: focus on Djankuat Glacier (Central Caucasus) / O.O. Rybak, E.A. Rybak // IOP Conference Series: Earth and Environmental Science. – 2018. – Vol. 107. DOI :10.1088/1755-1315/107/1/012041.
8. Fürst J. J. Improved convergence and stability properties in a three-dimensional higher-order ice sheet model / J. J. Fürst, O. Rybak, H. Goelzer and others. // Geoscientific Model Development. – 2011. – Vol. 4. – P. 1133-1149.
9. Blatter H. Velocity and stress fields in grounded glaciers: a simple algorithm for including deviatoric stress gradients / Blatter H. // Journal of Glaciology. - 1995. Vol. 41 (138). – 333-344.
10. Nemec J. Reconstruction of the surface mass balance of Morteratschgletscher since 1865 / J. Nemec, P. Huybrechts, O. Rybak and others // Annals of Glaciology. – 2009. – Vol. 50. – P. 126-134.
11. Петраков Д. А. Толщина льда, объем и современные изменения площади ледника Сары-Тор (массив Ак-Шыйрак, внутренний Тянь-Шань) / Д. А. Петраков, И. И. Лаврентьев, Н. В. Коваленко and others // Криосфера Земли. – 2014. – Т. 18. – №3. – C. 91-100.
12. Лаврентьев И. И. Толщина, объем льда и подледный рельеф ледника Джанкуат (Центральный Кавказ) / И.И. Лаврентьев, С. С. Кутузов, Д. А. Петраков и др. // Лед и Снег. – 2014. – № 4(128). – С. 7-19. DOI: http://dx.doi.org/10.15356/2076-6734-2014-4-7-19.
13. Пастухов В. Г. Полный массообмен ледника Джанкуат / В. Г. Пастухов - Дипломная работа. Москва: МГУ им. М.В. Ломоносова, географический факультет, кафедра криолитологии и гляциологии, 2011. – 150 с.
14. Поповнин В. В. Разрастание поверхностной морены на языке ледника Джанкуат за период прямого гляциологического мониторинга / В. В. Поповнин, А. А. Резепкин, Л. Г. Тиелидзе // Криосфера Земли. – 2015. – Т. 19. – № 1. – С. 89-98.
15. Рыбак О. О. Равновесные конфигурации ледника Джанкуат в разных климатических условиях / О. О. Рыбак, Е.А. Рыбак, И. А. Корнева и др. // Системы контроля окружающей среды. – 2018 – Вып. 14(33), в печати.
16. Zekollari H. On the climate–geometry imbalance, response time and volume–area scaling of an alpine glacier: insights from a 3-D flow model applied to Vadret da Morteratsch, Switzerland / H. Zekollari, P. Huybrechts // Annals of Glaciology. – 2015. – Vol. 56. – P. 51-62. DOI: 10.3189/2015AoG70A921

Список литературы на английском языке / References in English

1. Bahr D. B. The physical basis of glacier volume-area scaling. – / D. B. Bahr, M. F. Meier, S. D. Peckham // Journal of Geophysical Research. – 1997. - Vol. 102. – P. 20355–20362.
2. Adhikari S. Glacier volume-area relation for high-order mechanic and transient glacier states / S. Adhikari, S. J. Marshall // Geophysical Research Letters. – 2012. – Vol. 39. – L16505. DOI:10.1029/2012GL052712
3. Erasov N. V. Metod opredeleniya ob"ema gornyh lednikov [A method of determonation of volume of mountain glaciers] / N. V. Erasov // Materialy glyaciologicheskih issledovanij [Data of Glaciological Studies]. – 1968. – №. 14. – P. 307-308. [in Russian]
4. Bahr D. B. A review of volume-area scaling of glaciers / D. B. Bahr, W. T. Pfeffer, G. Kaser // Reviews of Geophysics. – 2015. – Vol. 53. – P. 95-140. DOI:10.1002/2014RG000470.
5. Rybak O. Kalibrovka matematicheskoj modeli dinamiki lednika Maruh, Zapadnyj Kavkaz [Calibration of a mathematical model of Marukh Glacier dynamics, Western Caucasus] / O.O. Rybak, E.A. Rybak, S.S. Kutuzov et al. // Led i sneg [Ice and snow]. – 2015. – Vol. 55. – No. 2. - P. 9-20. DOI: https://doi.org/10.15356/2076-6734-2015-2-9-20 [in Russian]
6. Rybak O. O. Model'nye raschety podmorennogo tayaniya na lednike Dzhankuat / O. O. Rybak, E. A. Rybak, I. A. Korneva // Sistemy kontrolya okruzhayushchej sredy. – 2018. – №. 12(32). – P. 86-92.
7. Rybak O. O. Model-based calculations of surface mass balance of mountain glaciers for the purpose of water consumption planning: focus on Djankuat Glacier (Central Caucasus) / O. O. Rybak, E. A. Rybak // IOP Conference Series: Earth and Environmental Science. – 2018. – Vol. 107. DOI :10.1088/1755-1315/107/1/012041.
8. Fürst J. J. Improved convergence and stability properties in a three-dimensional higher-order ice sheet model / J.J. Fürst, O. Rybak, H. Goelzer et al. // Geoscientific Model Development. – 2011. – Vol. 4. – P. 1133-1149.
9. Blatter H. Velocity and stress fields in grounded glaciers: a simple algorithm for including deviatoric stress gradients / Blatter H. // Journal of Glaciology. – – Vol. 41 (138). – P. 333–344.
10. Nemec J. Reconstruction of the surface mass balance of Morteratschgletscher since 1865 / J. Nemec, P. Huybrechts, O. Rybak O., J. Oerlemans // Annals of Glaciology. – 2009. – Vol. 50. – P. 126-134.
11. Petrakov D. A. Tolshchina l'da, ob"em i sovremennye izmeneniya ploshchadi lednika Sary-Tor (massiv Ak-SHyjrak, vnutrennij Tyan'-SHan') [Ice thickness, volume and modern change of the Sary-Tor glacier area (Ak-Shyirak massif, Inner Tian Shan)] / D.A. Petrakov, I.I. Lavrent'ev, N.V. Kovalenko, R.A. Usubaliev // Kriosfera Zemli [Earth's Cryosphere]. – 2014. – Vol. 18. – № 3. – P. 91-100. [in Russian]
12. Lavrent'ev I. I. Tolshchina, ob"em l'da i podlednyj rel'ef lednika Dzhankuat (Central'nyj Kavkaz) [Ice thickness, ice volume and sub-glacial relief of Djankuat Glacier (Central Caucasus)] / I.I. Lavrent'ev, S.S. Kutuzov, D.A. Petrakov et al. // Led i Sneg [Ice and Snow]. – 2014. – № 4(128) . – P. 7-19. [in Russian]
13. Pastuhov V. G. Polnyj massoobmen lednika Dzhankuat [Total mass exchange of Djankuat glacier] / V.G. Pastuhov - Diplomnaya rabota [Diploma paper]. Moskva: MGU im. M.V. Lomonosova, geograficheskij fakul'tet, kafedra kriolitologii i glyaciologii, 2011. – 150 p. [in Russian]
14. Popovnin V. V. Razrastanie poverhnostnoj moreny na yazyke lednika Dzhankuat za period pryamogo glyaciologicheskogo monitoringa [Superficial moraine expansion on the Djankuat glacier snout over the direct glaciological monitoring period] / V. V. Popovnin, A. A. Rezepkin, L. G. Tielidze // Kriosfera Zemli [Earth's Cryosphere]. – 2015. – Vol. 19. – № 1. – P. 89-98. [in Russian]
15. Rybak O. O. Ravnovesnye konfiguracii lednika Dzhankuat v raznyh klimaticheskih usloviyah [Equilibrium configurations of Djankuat glacier under various climatic conditions] / O. O. Rybak, E. A. Rybak, I. A. Korneva and others // Sisitemy kontrolya okruzhayushchej sredy [Systems of the environmental control]. – 2018 – No. 14(33), in press. [in Russian]
16. Zekollari H. On the climate–geometry imbalance, response time and volume–area scaling of an alpine glacier: insights from a 3-D flow model applied to Vadret da Morteratsch, Switzerland / H. Zekollari, P. Huybrechts // Annals of Glaciology. – 2015. – Vol. 56. – P. 51-62. DOI: 10.3189/2015AoG70A921