ИССЛЕДОВАНИЕ ПАРАМЕТРОВ СПОРТИВНОЙ ВЕРЕВКИ С ПОМОЩЬЮ ВИДЕОНАБЛЮДЕНИЯ.

ИССЛЕДОВАНИЕ ПАРАМЕТРОВ СПОРТИВНОЙ ВЕРЕВКИ С ПОМОЩЬЮ ВИДЕОНАБЛЮДЕНИЯ.

Научная статья

Макашова З.Э.^1, *, Чередниченко Л.А.², Чередниченко Ф.Л.³

^{1, 2} Балтийский государственный технический университет «ВОЕНМЕХ», Санкт - Петербург, Россия;

³ СПбГУ Центр патриотического воспитания молодежи «Дзержинец», Санкт-Петербург, Россия

* Корреспондирующий автор (zelmmak[at]yandex.ru)

Аннотация

В статье предложен метод исследования динамических процессов в спортивной веревке с помощью видеонаблюдения. Получены временные диаграммы падения груза с высоты 3м. Выполнен теоретический анализ характера движения груза и веревки. Показано, что на отдельных интервалах времени они могут перемещаться раздельно. Рассчитаны коэффициенты трения и упругости на введенных временных интервалах динамического процесса.

Ключевые слова: спортивная веревка, видеонаблюдение, коэффициенты трения и упругости веревки.

RESEARCH OF PARAMETERS OF A SPORTS ROPE WITH THE HELP OF VIDEO SURVEILLANCE

Research article

Makashova Z.E.^1, *, Cherednichenko L.A.², Cherednichenko F.L.³

^{1, 2} Baltic State Technical University “VOENMEH,” St. Petersburg, Russia;

³ SPbSU Center for the Patriotic Education of Young People “Dzerzhinets,” St. Petersburg, Russia

* Corresponding author (zelmmak[at]yandex.ru)

Abstract

The article proposes the method for studying dynamic processes in a sports rope with the help of video surveillance. The time diagrams of the fall of the cargo from the height of 3 meters were obtained. Theoretical analysis of the nature of the movement of cargo and rope is performed. It is shown that at individual time intervals they can be moved separately. The coefficients of friction and elasticity are calculated on the input time intervals of the dynamic process.

Keywords: sports rope, video surveillance, coefficients of friction and elasticity of the rope.

Спортивные веревки используются в различных типовых и экстремальных условиях. Принятая оценка их качества по статическим характеристикам и предельным усилиям в случае разрыва не позволяют судить о динамических нагрузках. Динамические испытания и последующий анализ результатов дают возможность определить реальные технические характеристики веревки. В статье предлагается метод исследования  динамики  с помощью видеонаблюдения.

Полный анализ динамического процесса в спортивной веревке возможен, если известны ее параметры: коэффициент трения к_т и коэффициент упругости к_у [1], [2], [3]. Однако в технических паспортах веревок они не приводятся, поскольку зависят от многих  факторов. Для получения параметров необходимо выполнить ряд экспериментальных  исследований.

Известные авторам экспериментальные стенды [4], [5], [6] позволяют измерить и записать силовое воздействие на веревку с использованием тензодатчиков и измерительных электронных схем. При этом можно снять статическую механическую характеристику веревки  F_у(x), где  x – ее удлинение под действием силового воздействия P = mg груза массой m, а также динамическое изменение силы упругости f_у (t). Подобные измерения позволяют определить как статический  коэффициент упругости веревки, так и динамические параметры, связанные с упругостью. Стремление к высокой точности измерений приводит к проявлению  на  осциллограммах высокочастотных колебаний опоры и размытию временной зависимости записываемого усилия. Сила трения при этом не исследуется.

Более информативным, но менее точным является метод видеонаблюдения за изменением длины веревки во время динамического процесса. Метод состоит в том, что деформация веревки  фиксируется видеокамерой, имеющей достаточную частоту кадров. По видеозаписи определяется положение нагруженного конца веревки или самого груза, а также соответствующее время.

В качестве примера рассмотрим вертикальное падение груза, закрепленного на конце веревки, второй конец которой крепится к опоре О (рис.1а). Далее исследованы случаи падения с фактором, равным 1.

В системе веревка - груз действуют три силы: сила инерции груза  f_и(t), сила трения  f_т(t) и сила упругости  f_у(t). Весом веревки пренебрежем. Уравнение, описывающее динамический процесс, имеет вид:

 f _и  +  f_т  +  f_у = P              (1) Если параметры веревки постоянны, т.е. выполняются законы Стокса и Гука, то уравнение (1) является линейным m x^' ' +  k_т x^'  + k_у x  = k_у x₀ = mg, где  x₀ – установившееся значение удлинения веревки.

Линейная модель исследовалась в работах [2], [3], [7], в которых подчеркнуто, что реальные динамические процессы в системе веревка – груз  носят нелинейный характер. Для изучения их особенностей и был разработан метод видеонаблюдения и выполнена серия опытов, в частности, связанных с падением груза. Эксперименты проводились в СПбГБУ ЦПВМ «Дзержинец» г.Санкт-Петербург под руководством педагога дополнительного образования по направлению «Спелеотуризм» Чередниченко Ф. Л. (2.04, 1 3.06.2018г.).

Опыты выполнялись в помещении высотой 7м, точка опоры находилась на удалении 1м от потолка, а от стены - на 0,5м. Использовались отечественные веревки производства заводов в Коломне и Дзержинске диаметром 10мм с начальными длинами  l_н = 3м. Масса груза 80кг. На стене была нанесена координатная сетка в районе движения груза с ячейкой (10 × 10) см², а также закреплена мерная лента с делением 1см. Район движения груза фотографировался видеокамерой GoPro 2, имеющей частоту кадров 120 к/мин.

Зависимости  x(t) положения конца веревки и  x₁(t) - положения груза воспроизводились в виде осциллограмм после раскадровки видеозаписи. Типовые графики этих функций в предположении совпадения центра тяжести груза с концом веревки представлены на рис.1б, а при несовпадении - на рис.2.

Рассмотрим с качественной стороны динамический процесс, осциллограмма которого воспроизведена на рис.1б. В течении времени 0…t₁  груз свободно падает с высоты  h = l_н. При этом потенциальная  энергия груза преобразуется в кинетическую энергию. В конце интервала груз приобретает скорость V₀ = ( 2 gl_н )^0,5

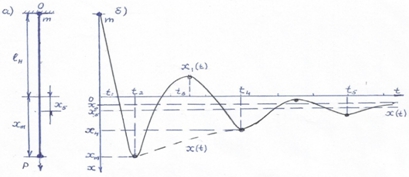
Рис. 1 – Схема опыта (а) и диаграммы зависимостей x (t) и x₁(t) при совпадении конца веревки с центром тяжести груза (б)

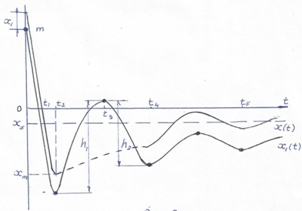
Рис. 2 – Диаграммы зависимостей x (t) и x₁(t) при несовпадении конца веревки с центром тяжести груза

 

Далее ( t₁…t₂ ) развивается динамический процесс в системе веревка -  груз: груз тормозится за счет потерь энергии на трение в веревке и ее упругости (натяжения). Движение описывается уравнением (1), В момент  t_2- деформация веревки достигает максимума  x  =  x_m. Кинетическая энергия груза при этом равна нулю, ибо полностью преобразовалась  в тепло и потенциальную энергию  растянутой веревки  W_пв = 0,5 k_у x_m².

Поскольку  максимальная сила упругости  F_уm (x_m) ˃ P,  груз в момент t₂₊ начинает движение вверх. Начальная скорость движения находится из равенства кинетической энергии груза и потенциальной энергии веревки

0,5mV₀₁²  = 0,5 k_у x_m² ,  V₀₁ = x_m (k_у/m)^0,5.

Она может быть определена также по высоте отскока  h₁ груза от точки максимального  падения  V₀₁ = ( 2 g h ₁)^0,5. Эти формулы приводят к одному результату, если учесть нелинейность механической характеристики веревки [3]. В интервале времени  t₂…t₄  веревка сжимается, поскольку не нагружена грузом. Процесс восстановления длины веревки силой упругости инерционен, поэтому система веревка – груз распадается на две подсистемы.

Груз выполняет «свободный» полет по вертикали. Процесс описывается уравнением (2)  

f _и = P,   x₁^{' '} =  g,               (2)

здесь  x₁ – координата центра тяжести груза. Решение этого уравнения имеет вид:

x₁^' = V₀₁ – g t ,  x₁ = x_m + V₀₁t – 0,5 g t².

Веревка складывается в «гармошку» и свободно сокращается. Процесс описывается с помощью  равенства

 f_т  +  f_у  = 0.           (3)

Если параметры считать постоянными, то из (3) имеем

k_т x^'  + k_у x = 0,

x = А e ^{–t /τ} , A = x_m / e ^{– t}₂ ^/τ , τ_л  =  k_т / k_у = (t₄ – t₂)/ln (x_m/x₄),

т.е. при линейном рассмотрении процесса длина веревки экспоненциально уменьшается до момента  t₄, когда груз, опускаясь, снова нагрузит веревку. На рис.1а и рис.2 соответствующий участок зависимостей  x (t) выделен штриховой линией. Заметим, что в зависимости от длины и параметров веревки можно ожидать повторные скачки груза с убывающей амплитудой.

На следующем интервале  t₄…t₅  система веревка – груз совершает колебания, описываемые уравнением (1) с  новыми начальными условиями. К концу процесса t ˃ t₅ колебания практически прекращаются, и груз медленно поднимается вверх за счет упругости веревки, достигая установившегося положения при x = x₀. Этот интервал времени самый продолжительный. При повторении опыта следует учитывать, что возможно наложение предыдущего процесса на последующий.

С помощью осциллограммы x (t) могут быть получены функции x^'(t),

 x^{' '}(t), например, графическим методом при относительно невысокой точности.

Перейдем к определению параметров веревки с учетом нелинейных связей  и результатов экспериментов для исследования составляющих силового воздействия.

Статический коэффициент упругости приближенно находится с помощью механической характеристики. Так, при F_у(x) = Р он равен k_у = Р/ x. При анализе переходного процесса целесообразно использовать динамический коэффициент упругости  k_ду = d F_у(x) /d x.

Поскольку механическая характеристика веревки имеет вид параболы и может быть аппроксимирована квадратической  параболой, будем считать зависимость  f_у(x) = ax² при  a = 10⁵/ l_н²   типовой аппроксимацией этой характеристики [2], [3], [8]. В этом случае  динамический коэффициент упругости  k_ду= 2 ax, т.е. зависит от деформации веревки.

Мгновенное значение коэффициента трения может быть найдено из уравнения (1), поскольку все его другие составляющие определены. Для выделенных интервалов рационально ввести некоторое среднее значение этого коэффициента. Найдем средний коэффициент трения на интервале  t₁…t₂  , когда скорость  нелинейно уменьшается, с помощью зависимости приближенно описывающей этот процесс:

x^' = b – c x²          (4)

При  x = 0 скорость равна  V₀, а при x = x_m она равна нулю, т.е.

x^' = V₀ (1 - x² / x_m² ).

Далее энергию, расходуемую на трение, определим как работу по растяжению веревки

W_т =  = 2 k_т1 V₀ x_m//3,

а с другой стороны эта энергия равна разности потенциальных энергий груза, расположенного на уровне точки опоры над точкой x = x_m, и взлетевшего после отскока на высоту h₁ (рис.1б)

W_т = mg( l_н + x_m - h₁).

Таким образом, среднее значение коэффициента трения на рассматриваемом интервале времени равно:

k_т1 = 3mg( l_н + x_m - h₁)/2 V₀ x_m.             (5)

Возможность использования приближения (4) подтверждается сопоставлением с расчетом для варианта средней скорости  x^'_ср =   x_m/( t₂ - t₁). Отличие составляет 5%.

На интервале времени  t₂…t₄ динамический  процесс в веревке описывается однородным нелинейным дифференциальным уравнением первого порядка

k_т2 x^'  + а x² = 0,      (6)

из которого следует  d t = - k_т2 d x/ а x² .

Интегрируя слева по  t  от  t₂ до t₄ и справа по x от  x_m  до  x₄, получим коэффициент трения на третьем временном интервале

k_т2 = а (t₄ – t₂) x_m x₄/ ( x_m - x₄ ).         (7)

Заметим, что постоянная времени этой части процесса может быть определена приближенно по формуле:

τ_н = k_т2/2а x₀ ˃ τ_л .

Колебательный процесс на четвертом интервале  описывается уравнением

m x^{' '} +  k_т3 x^'  + a x² = a x₀²,           (8)

а коэффициент трения находится по формуле:

k_т3 = mgh₂ / x^'_срx₄,          (9)

здесь h₂ – высота падения груза после отскока (рис.2).

Наконец, при  t ˃ t₅ колебания практически прекращаются, и груз медленно поднимается вверх за счет упругости веревки, достигая установившегося положения x = x₀. Коэффициент трения находится из уравнения (8) при

x^{' '} = 0. По аналогии с выводом k_т2 получим

d t =  kт4 d x/ а ( x52- x2).

После интегрирования до выбранной координаты t6 ˃˃ t5 найдем

kт4 = а ( t6 - t5 ) x0 / (arctg (x6 / x0) - arctg (x5/ x0)) ≈

≈ a ( t6 - t5 ) x02 / ( x6 – x5 )                                                      (10)

В таблице 1 приведены результаты обработки осциллограмм x(t), полученных при падении груза, подвешенного на новой веревке коломенского завода, и при свободной деформации этой веревки после снятия груза.  Значение x относится к удлинению веревки  в конце интервала времени, а ∆x – к изменению длины за время ∆t.

 

Таблица 1 – Результаты обработки осциллограмм

m (кг)		80				0
Интервал ∆ t (с)	t1	t2 – t1	t4 - t2	t5 – t4	t6 - t5	-
	0,77	0,17	0,96	0,96	600	8
x (м)	0	1,05	0,7	0,55	0,28	0,49
∆ x (м)	0	1,05	0,35	0,15	0,27	0,06
kт (Нс/м)	-	430	2,2 104	8,2 103	5,6 106	4 105

 

Отметим, что серия из четырех подобных опытов с другими веревками, а также узлами крепления веревки к опоре и груза к веревке показала, что данные соответствующих измерений и расчетов отличаются не более, чем на 30%, что, в частности, связано с сравнительно низкой точностью измерений координаты x. В условиях проводимых экспериментов длительность переходных процессов, связанных с падением  груза, в среднем составляла  2,2с, продолжительность  второго интервала ~ 0,2с, третьего и четвертого по ~ 1с.

Из предыдущего анализа и данных таблицы 1 следует, что динамический процесс в веревке развивается сложным образом. Он условно может быть разбит на четыре интервала времени с разным описанием закона изменения длины веревки. При этом коэффициент трения изменяется в широких пределах. Он растет с уменьшением скорости развития процесса.

Кроме исследования изменения коэффициента трения в динамике, видеонаблюдение позволяет косвенным методом определить силовые воздействия на веревку  f_у= ax² в  любой момент времени, в том числе максимальное усилие при  x = x_{m ,} а также изменение частоты колебаний системы на четвертом интервале. Так, в рассмотренном выше опыте f_уm = 12,2к Н, а частота растет от 1,7 до 2 Гц.

Таким образом с помощью видеонаблюдения и аналитических расчетов можно анализировать все составляющие динамического процесса в спортивной веревке. Такой анализ необходим при сопоставлении характеристик веревок разных производителей и типов, а также при сравнении параметров веревок бывших в употреблении и на хранении.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Петко Н.. Азбука одноверевочной техники. Перевод с болгарского / Н. Петко, 1991. С.22.
2. Макашова З. Э. Статическая нагрузка веревки, используемой троллеем. Материалы МНПК / З. Э. Макашова, Ф. Л. Чередниченко, Л. А. Чередниченко. - Вологда, 30.08,2017. С.36-38.
3. Макашова З. Э. О динамике спелеоверевки при падении груза. Сб. статей МНПК,ч.1,Уфа, МЦИИ / З. Э. Макашова, Ф. Л. Чередниченко, Л. А. Чередниченко Омега, сайнс, 2017. С.44-47.
4. Jacques G. Эксперименты в области механики при спелеоспасении / G. Jacques. 1994 - 1996.С.15
5. Long, M. Lyon, G. Lyon. Industrial rope access. Contract research. Report 364/ 2001.  С.26-29.
6. Ступаков А. А. Стенды исследования средств индивидуальной защиты от падения человека с высоты / А. .А Ступаков. Вестник МГСУ, 2015, №8. С. 130-140.
7. Макашова З. Э. Линейная модель процессов в веревке при движении спортсмена вверх / З. Э. Макашова, Ф. Л. Чередниченко, Л. А. Чередниченко. Сб. статей МНПК,ч.1,Уфа, МЦИИ Омега, сайнс, 2017. С.106-111.
8. Серафимов К. В. Веревка – как она есть. / К. В. Серафимов, 1989-96гг. С.70. URL: www.sumgan.com
9. Ступаков А. А. Безопасность и определение рисков работы на высоте от использования страховочного оборудования. Механизация строительства / А. А. Ступаков, №11(845), 2014. С.40-44.
10. Маринов В. Проблемы безопасности в горах. Физкультура и спорт / В. Маринов. 1981г. С.154-176.

Список литературы на английском языке / References in English

1. Petko N. Azbuka odnoverevochnoj tekhniki [Alphabet of single-rope technology]. Translation from Bulgarian / N. Petko, 1991. p.22.
2. Makashova Z.E. Staticheskaya nagruzka verevki, ispol'zuemoj trolleem. Materialy MNPK [The static load of the rope used by the trolley. Materials of MNPK] / Makashova Z.E., Cherednichenko F.L., Cherednichenko L.A., Vologda, 30.08,2017. Рр.36-38.
3. Makashova Z.E. O dinamike speleoverevki pri padenii gruza. Sb. statej MNPK [On the dynamics of caving in the fall of the load. Sat articles of MNPK, part 1] / Makashova Z.E., Cherednichenko F.L., Cherednichenko L., Ufa, Mtsii Omega, Sains, 2017. Pр.44-47
4. Jacques G. Ehksperimenty v oblasti mekhaniki pri speleospasenii [Experiments in the field of mechanics during speleospace] / G. Jacques. 1994 - 1996.Р.15
5. Long, M. Stendy issledovaniya sredstv individual'noj zashchity ot padeniya cheloveka s vysoty [Industrial rope access. Contract research] / A. Long, M. Lyon, G. Lyon.. Report 364/2001. Pр.26-29
6. Stupakov A. A. and other. Stands of research of means of individual protection against falling of the person from height. Vestnik MGSU, 2015, №8. Pp. 130-140.
7. Makashova Z. E. Linejnaya model' processov v verevke pri dvizhenii sportsmena vverh [Linear model of the processes in the rope when the athlete moves up. Sat articles of MNPK] / Makashova Z. E., Cherednichenko L. A., Cherednichenko F. L, part 1, Ufa, Mtsii Omega, Sains, 2017. P.106-111
8. Serafimov K.V. Rope - as it is. / K. V. Serafimov , 1989-96. C.70. URL: Www.sumgan.com
9. Stupakov A. A. Bezopasnost' i opredelenie riskov raboty na vysote ot ispol'zovaniya strahovochnogo oborudovaniya. Mekhanizaciya stroitel'stva [Safety and risk assessment work at heights from the use of safety equipment. Mechanization of construction] / A. A. Stupakov No. 11 (845), 2014. P.40-44.
10. Marinov V. Problemy bezopasnosti v gorah. Fizkul'tura i sport [Problems of safety in the mountains. Physical education and sport] / V. Marinov. 1981 P.154-176.