ФОКУСИРОВКА МАГНОНОВ В КРИСТАЛЛАХ СО СТРУКТУРОЙ АЛЬФА-ЖЕЛЕЗА

ФОКУСИРОВКА МАГНОНОВ В КРИСТАЛЛАХ СО СТРУКТУРОЙ АЛЬФА-ЖЕЛЕЗА

Научная статья Савченко С.П. * ORCID: 0000-0001-7760-8362, Институт физики металлов имени М.Н.Михеева УрО РАН, Екатеринбург, Россия

* Корреспондирующий автор (sergeysavch[at]mail.ru)

Аннотация Изучены особенности распространения спиновых волн (магнонов) в кристаллах со структурой альфа-железа в рамках модели, учитывающей взаимодействие атома с атомами первой и второй координационной сферы в слое кубической объёмно-центрированной кристаллической решетки. Показано, что в длинноволновом приближении фокусировка магнонов отсутствует, а для коротких волн в отсутствие внешнего постоянного магнитного поля наблюдается эффект фокусировки. Рассмотрены особенности фокусировки при отрицательном параметре взаимодействия с соседями. Ключевые слова: ОЦК-решетка, альфа-железо, фокусировка, магноны, гейзенберговское взаимодействие.

MAGNON FOCUSING IN CRYSTALS WITH ALPHA-IRON STRUCTURE

Research article Savchenko S.P. * ORCID: 0000-0001-7760-8362 M.N. Mikheev Institute of Metal Physics, UB of RAS, Ekaterinburg, Russia;

* Corresponding author (sergeysavch[at]mail.ru)

Abstract The features of the propagation of spin waves (magnons) in crystals with the alpha-iron structure are studied within the framework of a model that takes into account the interaction of an atom with the atoms of the first and second coordination spheres in a layer of a cubic body-centered crystal lattice. It is shown that there is no magnon focusing in long-wave approximation, as for short waves in case of no external constant magnetic field, a focusing effect is observed. The features of focusing are considered with a negative interaction parameter with neighbors. Keywords: bcc-lattice, alpha-iron, focusing, magnons, heisenberg interaction. Современная электроника имеет тенденцию к миниатюризации и активно осваивает терагерцовый диапазон. При этих условиях всё более важным вопросом становится задача теплоотвода, и, соответственно, уменьшение потерь на джоулево тепло. В связи с этим привлекательной областью исследования становится спинтроника и приобретает новую актуальность задача о распространении спиновых волн в соответствующих материалах, перспективных для спинтроники. Одним из таких материалов является альфа-железо. В нём обменное взаимодействие между атомами решётки хорошо описывается моделью Гейзенберга. Спиновые волны в рамках этой модели имеют достаточно сложный закон дисперсии. В частности, их фазовая и групповая скорости не коллинеарны и характеристики потока спиновых волн зависят от направления. В результате этого возникает анизотропия распространения спиновых волн, исследованию которой и посвящена настоящая работа. Перспективными объектами спинтроники считаются тонкие пленки и гетероструктуры, в которых спиновые волны распространяются вдоль поверхности. В связи с этим мы ограничиваемся рассмотрением двумерной задачи. Внешнее магнитное поле полагаем равным нулю, поскольку интересуемся собственной анизотропией распространения магнонов, то есть той, что обусловлена только структурой кристаллической решетки. Магнитные свойства альфа-железа, имеющего ОЦК структуру кристаллической решетки, хорошо описываются в рамках модели Гейзенберга, учитывающей взаимодействие спина атома с первыми и вторыми соседями. Гамильтониан гейзенберговского взаимодействия с первыми и вторыми соседями записывается следующим образом:

Закон дисперсии имеет вид: где  – постоянная обменной энергии,  – параметр, являющийся отношением величин обменного взаимодействия с первой и второй координационной сферой, S = 2.2 – среднее число магнетонов Бора на атом железа, взятое из [1]; J₁ и J₂ – постоянные обменного взаимодействия центрального атома с атомами первой и второй координационной сферы, для атомов железа в слое [2]  J₁ = 0.78 mRy и J₂ = 0.18 mRy, следовательно ξ≈0.235; q(φ) = (qcos(φ), qsin(φ)) – волновой вектор; a = 2.866 Å – период решётки. Здесь стоит также отметить, что в приближении длинных волн (при малых q) анизотропия спектра становится несущественной, что доказывается разложением (2) по малому параметру:

В дальнейшем будет показано, что с увеличением модуля волнового вектора увеличивается и анизотропия распространения спиновых волн. Определить направления фокусировки и дефокусировки магнонов можно по форме изоэнергетических поверхностей, поскольку групповая скорость перпендикулярна изоэнергетической поверхности в заданной точке и определяет поток магнонов. Для построения поверхностей постоянной энергии вычисляются значения модуля волнового вектор q (φ) из уравнения w (q)=const и строятся соответствующие кривые. Для количественного описания эффекта фокусировки магнонов применим метод, развитый Марисом в работе [3] для оценки фокусировки фононов. Автор в своей работе воспользовался моделью изотропного потока для сравнения с анизотропным и ввёл понятие коэффициента усиления потока фононов A(θ,φ) — отношения интенсивности анизотропного потока квазичастиц в заданном направлении к интенсивности потока в предположении изотропной среды. Величина коэффициента усиления в двумерном случае может быть вычислена по формуле A(φ) = q/|K|, где K-гауссова кривизна поверхности постоянной энергии. Применение указанных методов позволило установить, что анизотропия потока магнонов возрастает по мере приближения частоты к границе первой зоны Брюллиэна. Показано, что магноны фокусируются в направлении [10], где A изменяется от 1 до 2.7, и дефокусируются в направлении [11] - A изменяется от 1 до 0.36. Указанные предельные значения A наблюдаются у спиновых волн c частотой 360 ТГц (у границы первой зоны Бриллюэна). Зависимости коэффициента A(φ), а также кривые постоянной энергии q(φ) приведены на рисунке 1.

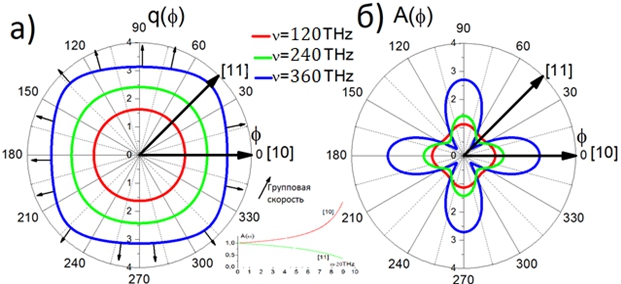
Рис. 1 – Картина фокусировки спиновых волн в слое альфа-железа

На рисунке (а) приведена поверхность постоянной энергии. Стрелками перпендикулярно изоповерхности показаны направления групповых скоростей. На рисунке (б) все три кривые коэффициента усиления потоков разных энергий пересекаются в окрестности одних и тех же точек, что означает сохранение диапазонов фокусировки и дефокусировки независимо от энергии спиновых волн. На врезке посередине изображено возрастание и убывание коэффициента усиления A(ω) в характерных направлениях [10] и [11]. По виду этой врезки можно заключить, что коэффициент усиления не имеет экстремумов при увеличении модуля волнового вектора от 0 до границы первой зоны Бриллюэна. Применение методов к системе с отрицательным параметром ξ (что равносильно отрицательному J₁ или J₂)   показало, что в этом случае на некоторых направлениях эффект фокусировки возрастает на порядки, иначе говоря на этих направлениях формируется каустика магнонов. Так, при ξ = -0,235 в направлении [11] происходит наиболее сильная дефокусировка с коэффициентом A≈0,01, в [10] присутствует небольшая фокусировка с A=5,8. Каустика наблюдается при углах ±8º от [11]. Картина фокусировки для случая ξ=-0,235 приведена на рисунке 2.

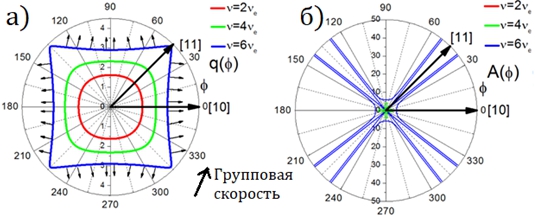
Рис. 2 – Картина фокусировки магнонов при взаимодействии с ближайшими атомами, равном ξ=-0,235

На изоповерхности (рисунок (а)) видны вогнутые участки, связанные с появлением каустик. По зависимостям коэффициента усиления (рисунок (б)) видно, что у спиновых волн высокой частоты есть направления, где A(θ) имеет расходимость. В этих направлениях кривизна изоповерхности резко уменьшается и, соответственно, величина коэффициента усиления резко возрастает, то есть появляется каустика магнонов. Поведение коэффициента усиления в направлении [10] обусловлено, как и на рисунке 1, совместным влиянием как первых, так и вторых соседей. Отдельное внимание стоит уделить поведению каустик в зависимости от параметра взаимодействия ξ. Здесь влияние атомов первой и второй координационной сферы сдвигает направление каустики к кристаллографическому направлению [11]. В самом направлении [11] возрастает величина дефокусировки от А=0.07 при ξ=-0.1 до A=0.02 при ξ=-0.8. В [10] фокусировка изменяется от A=17 до A=1.7, что можно объяснить совместным влиянием атомов первой и второй координационной сферы. При ξ=-0.8 направления каустик повёрнуты от [11] на угол 8°, при ξ =-0.1 на 20°. Направления каустик для двух случаев изображены на рисунке 3.

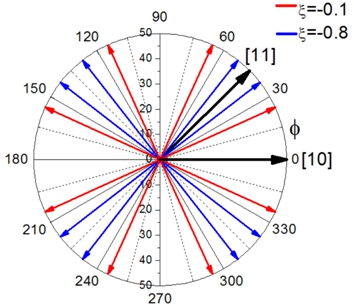
Рис. 3 – Направления каустик для разных значений параметра ξ

Таким образом, показано, что в альфа-железе в отсутствие внешнего постоянного магнитного поля должна наблюдаться фокусировка коротковолновых магнонов, т. е. магнонов с волновыми векторами вблизи границы первой зоны Бриллюэна. Для отрицательного параметра взаимодействия с соседями показано формирование каустик, также исследовано их поведение в зависимости от величины этого параметра.

Список литературы / References

1. Kittel С. Quantum Theory of Solids/ C. Kittel - New York: Wiley, 1963. – 435 p.
2. Мамонова М. В. Расчет коэффициента магнитосопротивления для мультислойной магнитной структуры Fe/Cr / М. В.Мамонова, В. В. Прудников, П. В. Прудников и др. // Вестник омского университета. - 2016 -№ 3. - С. 16–19
3. Maris H. J. Enhancement of Heat Pulses in Crystals due to Elastic Anisotropy / H. J.Maris // J. Acoust. Soc. Am. – 1971. – Vol.50. – p. 812-818 doi.org/10.1121/1.1912705
4. Jasiukiewicz Cz. Phonon focusing patterns: Calculation of response of finite area detectors to pulsed ballistic beams of dispersive and dispersionless phonons / Cz. Jasiukiewicz, T. Paszkiewicz, and D. Lehmann // Zeitschrift Zur Physik B Condensed Matter. – 1994. – Vol. 96. – P. 213-222. doi: 10.1007/BF01313286
5. Jacob Philip Phonon magnification in cubic crystals / Jacob Philip, K.S.Viswanathan // Physical Review B.-1978.- Vol.17.- P.4969-4978. doi: 10.1103/PhysRevB.17.4969
6. Lax and V. Narayanamurti Phonon magnification and the Gaussian curvature of the slowness surface in anisotropic media: Detector shape effects with application to gas / M. Lax and V. Narayanamurti // Physical Review B.-1980.-Vol.22.-P.4876-4897. doi: 10.1103/PhysRevB.22.4876
7. Northrop G. A. Ballistic phonon imaging in germanium / G. A. Northrop, J. P.Wolfe // Physical Review B.-1980.-Vol.22.-P.6196-6212. doi: 10.1103/PhysRevB.22.6196
8. Wolfe J. P. Imaging Phonons Acoustic Wave Propagation in Solids / J. P. Wolfe.- Cambridge: Cambridge University Press, 1998.-411 p.
9. Kohler H. Spin waves and Heisenberg exchange constants for α-iron / H. Kohler, J. Sticht and J. Kubler / Physica B.-1991.-Vol.172.-P.79-84. doi: 11016/0921-4526(91)90419-f
10. Hai Wang Exchange interaction function for spin-lattice coupling in bcc iron / Hai Wang, Pui-Wai Ma, and C. H. Woo / Physical Review B.-2010.-Vol.82.-144304.-P.1-8. doi: 10.1103 /PhysRevB.82.144304