ЭЛЕКТРИЧЕСКИЙ ТОК И ПРОВОДИМОСТЬ В УЛЬТРАХОЛОДНОЙ ПЛАЗМЕ. РАСЧЕТ МЕТОДОМ МОЛЕКУЛЯРНОЙ ДИНАМИКИ

ЭЛЕКТРИЧЕСКИЙ ТОК И ПРОВОДИМОСТЬ В УЛЬТРАХОЛОДНОЙ ПЛАЗМЕ. РАСЧЕТ МЕТОДОМ МОЛЕКУЛЯРНОЙ ДИНАМИКИ

Научная статья

Бобров А.А.^1, *, Бронин С.Я.², Зеленер Б.Б.³, Зеленер Б.В.^{4 1, 2, 3, 4} Объединенный институт высоких температур РАН, Москва, Россия; ³ Национальный исследовательский университет – Московский энергетический институт, Москва, Россия; ³ Национальный исследовательский университет – Московский инженерно-физический институт, Москва, Россия

* Корреспондирующий автор (abobrov[at]inbox.ru)

Аннотация

В работе методом молекулярной динамики исследован электрический ток в ультрахолодной сильно неидеальной плазме. Ток вызывается электрическим полем, приложенным к плазме. Расчеты сделаны для разных значений параметра неидеальности. Проводимость плазмы определялась из отношения тока и электрического поля. Проведено сравнение с результатами, полученными другими методами. Обсуждается отличие от результатов, полученных ранее на основе анализа коэффициента диффузии и автокорреляционной функции тока.

Ключевые слова: молекулярная динамика, неидеальная плазма.

ELECTRICAL CURRENT AND CONDUCTIVITY IN ULTRACOLD PLASMA. CALCULATION BY THE METHOD OF MOLECULAR DYNAMICS

Research article

Bobrov A. А.^1, *, Bronin S. Ya.², Zelener B. B.³, Zelener B. V.^{4 1, 2, 3, 4} Joint Institute for High Temperatures of RAS, Moscow, Russia; ³ National Research University – Moscow Power Engineering Institute, Moscow; Russia; ³ National Research University – Moscow Engineering Physics Institute, Moscow; Russia;

* Corresponding author (abobrov[at]inbox.ru)

Abstract

Electric current in the ultracold highly collisional plasma was considered in the work by the method of molecular dynamics. The current is caused by the electric field applied to plasma. Calculations are made for different values of the collisional parameter. Plasma conductivity was determined from the ratio of current and electric field. Comparison with the results obtained by other methods was performed. The difference from the results obtained earlier on the basis of the analysis of the diffusion coefficient and the autocorrelation function of the current is discussed.

Keywords: molecular dynamics, collisional plasma. Введение

Ультрахолодная плазма – это плазма, получаемая при температуре несколько кельвинов при ионизации атомов, охлаждаемых в магнитооптической ловушке. Впервые такая плазма была получена в 1999 [1], [2], [3]. Ультрахолодная плазма имеет ряд особенностей, позволяющих моделировать кинетические процессы сильно неидеальных кулоновских систем. В частности, ультрахолодная плазма является нейтральной и полностью ионизованной плазмой, поэтому ее свойства определяются исключительно столкновениями заряженных частиц. Это важное отличие от обычной низкотемпературной плазмы, где важную роль играют столкновения заряженных частиц с нейтральными.

Ультрахолодная плазма, как правило, сильно неидеальная, так как она производится из ультрахолодного атомного газа, который может быть приготовлен при относительно высокой плотности. Когда атомы ионизуются лазером, температура образующихся электронов определяется разницей энергии фотона и потенциала ионизации атома. Эта разница может быть очень мала – всего несколько кельвинов.

Теоретическое рассмотрение сильно неидеальной плазмы существенно затруднено в силу отсутствия малого параметра (в качестве которого в слабонеидеальной плазме служит отношение длины Ландау к радиусу Дебая), поэтому для решения задач в области сильной неидеальности используют различные численные методы. Ранее в [4] мы исследовали численным методом молекулярной динамики коэффициент самодиффузии ионов в сильно неидеальной плазме. Наши результаты находятся в хорошем согласии с недавними экспериментами [5] по определению коэффициента самодиффузии в ультрахолодной плазме. Также мы рассчитали коэффициент диффузии электронов, экспериментальных данных для которого еще нет.

В рамках одноэлектронного приближения по коэффициенту диффузии для электронов мы оценили электрическую проводимость в широком диапазоне параметра неидеальности плазмы.

Необходимо отметить, что наши результаты [4] для диффузии в ультрахолодной плазме хорошо согласуются с оценкой диффузии работы [6], в которой методом молекулярной динамики моделировалась горячая плотная плазма, но с тем же значением параметра неидеальности. В [6] также определялась проводимость, но другим методом – по автокорреляционной функции тока, и этот результат не совпадает с оценкой проводимости [4]. И в [4] и в [6] проводимость оценивалась непрямыми методами и в настоящей работе мы представляем расчет проводимости прямым методом – используя моделирование электрического тока в плазме.

Теоретическая модель

Ультрахолодная плазма, получаемая в экспериментах является существенно неравновесной и нестационарной системой. Равновесная степень ионизации, которая получается из распределения Больцмана, должна обратится в ноль при таких низких температурах. Но, как наблюдается в экспериментах и показано в теоретических работах, главный процесс, приводящий к рекомбинации, – тройная рекомбинация, – существенно подавлен в ультрахолодной плазме. Причиной низкой скорости рекомбинации является существенная неидеальность плазмы. Ультрахолодная плазма с высокой степенью ионизации наблюдается в экспериментах в течение длительных времен – до десятков микросекунд.

В типичных экспериментальных условиях ультрахолодная плазма также не находится в термическом равновесии. Температуры электронов T_в и ионов T_p устанавливаются независимо, однако, в силу большого различия масс электронов и ионов, обмен энергиями между этими подсистемами очень медленный. В нашей работе, мы рассмотрели кинетику полностью ионизованной ультрахолодной сильно неидеальной плазмы. Мы моделировали плазму на временах, много меньших как характерного времени рекомбинации, так и времени электрон-ионного обмена энергиями. Это позволило нам рассматривать плазму, как квазистационарную и квазиравновесную систему. Для моделирования ультрахолодной плазмы мы использовали метод молекулярной динамики. Мы рассматривали кубическую ячейку моделирования, заполненную заряженными частицами – электронами и ионами (протонами). Для частиц мы решали классические уравнения движения. Мы рассматривали нейтральную плазму. Неизмененный кулоновский потенциал использовался для учета межчастичного взаимодействия как для одноименных, так и для разноименных зарядов. Для описания поведения частиц при близких пролетах, мы использовали метод “leapfrog” с переменным шагом по времени. В рассматриваемых условиях мы ограничились решением классических уравнений движения, поскольку среднее расстояние между частицами было много больше длины волны ДеБройля для частиц. Что касается образования атомов, единственным процессом рекомбинации в ультрахолодной плазме является трехчастичная рекомбинация, при которой за рассматриваемые времена могут образоваться только высоковозбужденные связанные состояния. Эти состояния описываются классической механикой с высокой степенью точности. Что касается образования атомов, единственным процессом рекомбинации в ультрахолодной плазме является трехчастичная рекомбинация, при которой за рассматриваемые времена могут образоваться только высоковозбужденные связанные состояния. Эти состояния описываются классической механикой с высокой степенью точности. В работе мы рассмотрели системы, состоящие из 1000 частиц в ячейке моделирования (N_в = 500 электронов и N_p  = 500 протонов). Размер ячейки моделирования выбирался из соотношения задаваемой концентрации электронов n_в и числа  N_в электронов. Начальные координаты частиц в ячейке задавались случайным образом. Начальные скорости частиц задавались так, чтобы суммарные кинетические энергии электронов и ионов равнялись заданным значениям (E_в (0) и Е_p (0)  и  соответственно). Более детальное описание моделирования см. в работе [4]. Для моделирования электрического тока в плазме, электрическое поле Е прикладывалось к ячейке моделирования, спустя некоторое время после начала интегрирования уравнений движения. Задержка включения поля требовалась для установления электронной температуры. Электрическое поле направлялось вдоль одного из ребер ячейки (параллельно оси x). Результаты и обсуждение В настоящей работе мы численно моделировали плазму для концентрации электронов  и начальной энергии электронов из интервала E_в = 2 - 30 К, что соответствует сильно неидеальной плазме. Неидеальность плазмы приводит к известному эффекту нагрева “disorder induced heating” [7]: после начала вычислений кинетическая энергия электронов быстро растет в течение времени, примерно равного обратной плазменной частоте:

где m_p  - масса электрона, в  – элементарный заряд. После нагрева электроны получают энергию порядка энергии на среднем расстоянии , устанавливается равновесная температура электронов и включается поле. Приложенное электрическое поле приводит к протеканию тока по плазме вдоль оси x. Для предотвращения появления нелинейных эффектов, таких как образование убегающих электронов, мы в расчетах использовали малое значение поля E по сравнению с критическим полем E_c (при котором доля убегающих электронов становится значительной) [8]:

где L - это кулоновский логарифм: Ток рассчитывался по формуле: где  - это скорость j-го электрона в момент времени t.

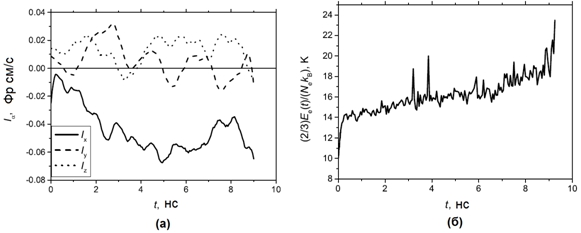
Рис. 1 – Электрический ток (а) и кинетическая энергия на один электрон (б) для одного из расчетов для n_в = 10¹⁰ см^-3,  T_в (0) = 10 К, E = 3 · 10^-4  статВ/см

На рис. 1 типичные временные зависимости тока и соответствующей суммарной кинетической энергии электронов представлены для одного из расчетов для n_в = 10¹⁰ см^-3   и T_в (0) = 10 К. Электрическое поле, равное E = 3 · 10^-4  статВ/см было включено в расчете в момент времени t = 1 нс. Для этих условий значение критического поля составляет примерно E_c   статВ/см, что в 20 раз превышает значение поля, использованного в этом расчете. На рис. 1(б) хорошо виден быстрый рост энергии электронов из-за первичного разогрева, за которым следует медленный джоулев нагрев. Так как мы использовали малые значения электрического поля в расчетах, рост температуры электронов из-за протекания тока был очень медленным.

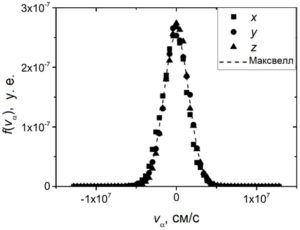
Рис. 2 – Распределение электронов по проекциям скоростей для расчета на рис. 1 в момент времени t = 5  нс. Точки – результат расчета, линия – распределение Максвелла для  T_в = 15 К

На рис. 2 распределения  электронов по проекциям скоростей на оси координат показаны для расчета, результаты которого представлены на рис. 1. Из рисунка видно, что искажение распределения вдоль оси x  незначительно и эффектом убегания электронов можно пренебречь. Для определения проводимости  использовалось следующее выражение для плотности тока: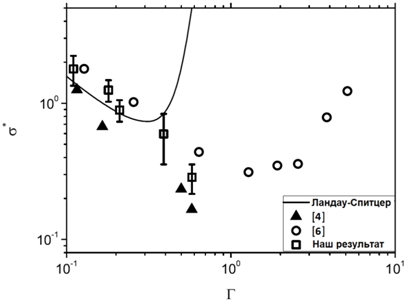 Удобно представить проводимость в безразмерном виде:

Рис. 3 – Безразмерная проводимость; проводимость по Ландау-Спитцеру получена с использованием частоты столкновений из [9]

На рис. 3 представлены результаты расчетов безразмерной проводимости в зависимости от параметра неидеальности плазмы Г = в² / (Т_ва), где а = (4πn_в/3)^-1/3. Теоретическая зависимость Ландау-Спитцера представлена сплошной линией. Для расчета проводимость мы усредняли траектории, полученные молекулярной динамикой за относительно короткие времена, так что рост температуры электронов из-за выделения джоулева тепла не превышал 10%. В результате, погрешность Г не превышает размера точек на рис. 3. Но это, в свою очередь, приводит к довольно большой неопределенности в оценке электрического тока, что является главным источником погрешности определения проводимости, как видно на рис. 3. Для всех представленных результатов значение использованного в расчетах электрического поля  было на порядок (и более) меньше соответствующего значения критического поля E_c. Так как на рис. 3 проводимость приведена в безразмерном виде в зависимости от Г, то мы можем сопоставить наши результаты для ультрахолодной плазмы с результатами, полученными для горячей и плотной плазмы [6]. В работе [6] проводимость рассчитывалась с использованием функции автокорреляции тока. Из рисунка видно, что результаты нашей настоящей работы хорошо согласуются с [6] для умеренной неидеальности, однако начиная с Г  0.5 начинают расходиться. Мы считаем, что причиной этого расхождения является использование в [6] модифицированного потенциала Кулона. В [6] использовался потенциал Кельбга для описания электрон-ионных взаимодействий и, по-видимому, это влияет на результаты в области большой плотности и сильной неидеальности. На рис. 3 приведены также наши предыдущие результаты [4]. В [4] мы получали проводимость на основе расчета автокорреляционной функции скорости (VAF). Из VAF мы получали оценку эффективной частоты столкновений электронов, на основе которой мы делали оценку проводимости. Видно, что результаты [4] отличаются как от результатов настоящей работы, так и от [6]. Это отличие можно объяснить тем фактом, что на проводимость влияют только столкновения электронов и ионов. Столкновения же электронов между собой на проводимость не влияют, так как при этом полный импульс электронов сохраняется. А эффективная частота столкновений содержит в себе вклады и ион-электронных, и элекрон-электронных столкновений. К похожему выводу пришли и авторы работы [10] при исследовании слабонеидеальной плазмы. На рис. 3 приведены также наши предыдущие результаты [4]. В [4] мы получали проводимость на основе расчета автокорреляционной функции скорости (VAF). Из VAF мы получали оценку эффективной частоты столкновений электронов, на основе которой мы делали оценку проводимости. Видно, что результаты [4] отличаются как от результатов настоящей работы, так и от [6]. Это отличие можно объяснить тем фактом, что на проводимость влияют только столкновения электронов и ионов. Столкновения же электронов между собой на проводимость не влияют, так как при этом полный импульс электронов сохраняется. А эффективная частота столкновений содержит в себе вклады и ион-электронных, и элекрон-электронных столкновений. К похожему выводу пришли и авторы работы [10] при исследовании слабонеидеальной плазмы. Заключение В настоящей работе было проведено моделирование тока в ультрахолодной неидеальной плазме методом молекулярной динамики. Электрическая проводимость была оценена прямым методом на основе зависимости протекающего по плазме тока от приложенного поля. Проведено сравнение безразмерной проводимости с результатами, полученными другими непрямыми методами. Проанализировано отличие результатов других работ от результатов расчетов проводимости, полученных в настоящей работе.

Финансирование Работа поддержана Программой фундаментальных исследований Президиума Российской академии Наук «Исследование вещества в экстремальных состояниях» под руководством академика Фортова В.Е.	Funding This work was supported by the Basic Investigations Program of the Presidium of the Russian Academy of Sciences “Study of Substance in Extreme States” under the guidance of Academician Fortov V.Е.
Конфликт интересов Не указан.	Conflict of Interest None declared.