АНАЛИЗ СТЕПЕНИ ВАРИАЦИИ ПАРАМЕТРОВ ВЫСОКОВОЛЬТНЫХ ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ

АНАЛИЗ СТЕПЕНИ ВАРИАЦИИ ПАРАМЕТРОВ ВЫСОКОВОЛЬТНЫХ ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ

Научная статья

Иванов И.Е. *

ORCID: 0000-0002-9975-8385,

Ивановский государственный энергетический университет имени В.И. Ленина, Иваново, Россия

* Корреспондирующий автор (iivanov[at]mtu.edu)

Аннотация

В работе исследуется потенциальная степень изменения параметров высоковольтных воздушных линий электропередачи – сопротивлений и проводимостей прямой и нулевой последовательностей – в зависимости от погодных условий и уровня загрузки линии. На основе анализа основных факторов, наибольшим образом влияющих на вариацию параметров линий, определены несколько режимов, характеризуемых различными соотношениями температуры окружающей среды и других характеристик. Для каждого из режимов выполнена серия вычислительных экспериментов по расчету матриц сопротивлений и проводимостей линии. Эксперименты осуществлялись на основе различных конфигураций – двухцепной линии напряжением 500 кВ, расположенной в России, и одноцепной линии напряжением 345 кВ, функционирующей в США. В результате установлено, что отдельные параметры воздушных линий могут варьироваться вплоть до 30–40 %, что свидетельствует о необходимости их постоянной актуализации.

Ключевые слова: воздушная линия электропередачи, параметры прямой последовательности, параметры нулевой последовательности, проводимость, синхронизированные векторные измерения, сопротивление.

INVESTIGATION OF THE VARIATIONS OF OVERHEAD HIGH VOLTAGE TRANSMISSION LINE PARAMETERS

Research article

Ivanov I.E. *

ORCID: 0000-0002-9975-8385,

Ivanovo State Power Engineering University, Ivanovo, Russia

* Corresponding author (iivanov[at]mtu.edu)

Abstract

The research is aimed at investigating how overhead transmission line parameters (positive and zero sequence impedances and admittances) could change under different weather and line loading. Analysis of the key factors having to do with line parameter variation has made it possible to sketch out a set of operational scenarios with different boundaries on the ambient temperature and other characteristics. Each of the scenarios was then used to compute a number of line impedance and admittance matrices.  Two different line configurations were exploited during the simulations: a 500 kV double circuit line from the Russian power system, and a 345 kV single circuit line from the US power grid. The obtained results suggest that some of the line parameters can experience variations of up to 30–40 %, which clearly shows the need for their regular correction.

Keywords: overhead transmission line, positive sequence parameters, zero sequence parameters, admittance, synchronized phasor measurements, impedance.

Введение

С появлением технологии синхронизированных векторных измерений (СВИ) появилась потенциальная возможность актуализации параметров элементов электрических сетей, в том числе высоковольтных воздушных линий электропередачи (ВЛЭП) [1], [2]. При этом количество отечественных и зарубежных публикаций, в которых детально анализировалась бы степень вариации отдельных сопротивлений и проводимостей ВЛЭП, крайне незначительно. В [3] анализируются возможные причины изменения параметров линий, и на основе большого объема вычислительных экспериментов выяснено, что основными влияющими факторами (ОВФ) можно считать следующие: средние высоты проводов и грозозащитных тросов (с учетом стрел провеса); удельная проводимость грунта вдоль трассы ВЛЭП; удельное сопротивление постоянному току материала проводов ВЛЭП; относительная магнитная проницаемость грозозащитного троса. Все остальные геометрические характеристики и физические свойства, необходимые для расчета матриц сопротивлений и проводимостей ВЛЭП, либо известны достаточно точно, либо оказывают пренебрежимое в количественном смысле влияние в рамках своих диапазонов неопределенности. Совершенно очевидно, что на практике выявленные ОВФ могут изменяться одновременно, поэтому возникает вопрос, каким образом оценить их совокупное (а не по отдельности) влияние на вариации параметров ВЛЭП, чтобы получить количественные данные о возможных изменениях сопротивлений и проводимостей прямой и нулевой последовательностей ВЛЭП. При этом необходимо понимать, что обозначенные выше ОВФ не являются полностью не зависимыми друг от друга. Поэтому было бы ошибочным просто генерировать произвольный вектор значений этих характеристик в пределах жестко заданного диапазона для каждой из них. Следовательно, возникает задача более реалистичного моделирования изменения ОВФ (и, как следствие, параметров ВЛЭП). Результаты анализа могут служить базой для совершенствования методов актуализации параметров ВЛЭП с применением современных технологий мониторинга (таких как СВИ).

Описание вычислительных экспериментов

Для решения поставленной задачи необходимо рассмотреть несколько различных режимов функционирования ВЛЭП, задавая для каждого из них свои диапазоны значений ОВФ. Анализ будем осуществлять на основе двух различных моделей ВЛЭП – двухцепной напряжением 500 кВ, расположенной на территории Российской Федерации, и одноцепной напряжением 345 кВ, расположенной в США. Конфигурация российской ВЛЭП отражена в [3, С. 32–33], а американской – данными, представленными на рисунке 1 и в таблице 1. Матрицы сопротивлений и проводимостей линий вычисляются на базе выражений, приведенных в [4], [5].

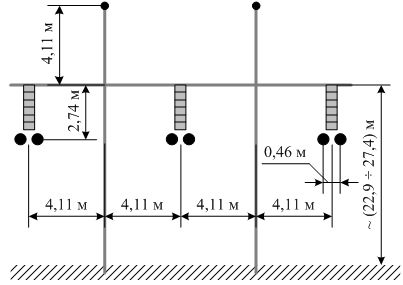
Рис. 1 – Конфигурация американской ВЛЭП напряжением 345 кВ, используемая для выполнения вычислительных экспериментов

 

Таблица 1 – Значения параметров американской ВЛЭП напряжением 345 кВ, необходимых для вычисления элементов матриц сопротивлений и проводимостей

Параметр	Значение	СИ
Горизонтальное расположение фазных проводников (см. рисунок 1)	[ -8,2296, 0, 8,2296 ]	м
Горизонтальное расположение грозозащитных тросов (см. рисунок 1)	[ -4,1148, 4,1148 ]	м
Вертикальное расположение фазных проводников*	[ 15, 15, 15 ]	м
Вертикальное расположение грозозащитных тросов*	[ 25, 25 ]	м
Внутренний радиус фазного проводника**	0,5067∙10-2	м
Внешний радиус фазного проводника**	1,5189∙10-2	м
Внутренний радиус грозозащитного троса**	0	м
Внешний радиус грозозащитного троса**	0,4602∙10-2	м
Относительная магнитная проницаемость фазных проводников и грозозащитных тросов	10,9173	о.е.
Удельное сопротивление постоянному току материала фазных проводников (при 20˚ C)***	3,7828/108	Ом∙м
Удельное сопротивление постоянному току материала грозозащитных тросов (при 20˚ C)***	2,2445/107	Ом∙м
Удельная проводимость грунта	0,01	См/м
Относительная магнитная проницаемость грунта	1	о.е.
Относительная диэлектрическая проницаемость грунта	10	о.е.
Частота	60	Гц
Количество проводников в расщепленной фазе	2	–
Радиус расщепления	22,86∙10-2	м
Дополнительная информация
Грозозащитные тросы непрерывно заземлены (т.е. они учитываются при вычислении элементов обеих матриц – [Z] и [Y])

Примечания: * Средние высоты подвеса проводов по трассе ВЛЭП ниже по сравнению с соответствующими высотами подвеса на опоре (см. рисунок 1) из-за наличия стрелы провеса; ** марка фазного провода – "ACSR 54/7 Cardinal" (сталеалюминиевый провод), а марка грозозащитного троса – "3/8’’ EHS" (стальной провод повышенной прочности); *** удельные сопротивления материала в Ом∙м были рассчитаны на основе данных о радиусах проводов, а также их погонном активном сопротивлении, равном 0,0587 Ом/км для фазных проводников и приблизительно равном 3,37 Ом/км для грозозащитных тросов.

Для того чтобы результаты осуществляемых экспериментов оказались достаточно достоверными, необходимо внимательно проанализировать не только возможные диапазоны изменения варьируемых характеристик линии, но и законы их изменения, а также корреляцию с различными влияющими факторами. Так, фактически все ОВФ зависят от температуры окружающей среды (ТОС); удельные сопротивления материала фазных проводов и грозозащитных тросов, а также величина стрелы провеса являются функцией не только ТОС, но и протекающего по ВЛЭП тока.

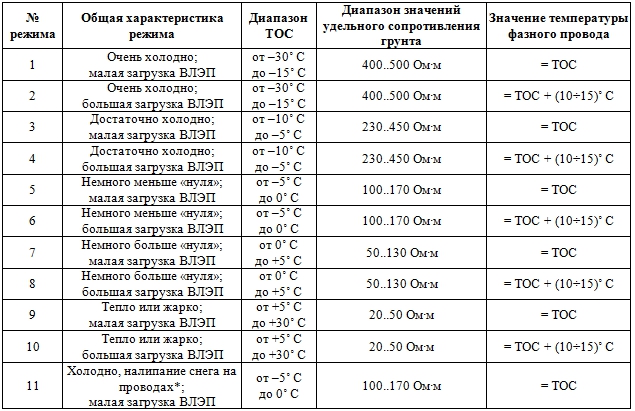
Удельное сопротивление грунта крайне нелинейно зависит от температуры и процентного содержания влаги [6]. При этом, как следует из [6, рисунок 11.29], крутизна графика зависимости сопротивления от температуры существенно варьируется, и зависимость имеет более пологий характер в области «плюсовых» температур. Кроме того, в районе «нуля» градусов имеется «скачок», связанный с переходом влаги, содержащейся в почве, из одного агрегатного состояния в другое [6], [7]. Указанные обстоятельства приводят к необходимости разделить принятый к рассмотрению температурный диапазон от –30˚ C до +30˚ C на множество участков (таблица 2). Выбор границ отдельных температурных интервалов и соответствующих значений удельного сопротивления грунта осуществлен на основе зависимостей, отраженных в [6, рисунки 11.28, 11.29]. Общий диапазон значений сопротивления – от 20 до 500 Ом∙м – продиктован анализом данных для характерных типов почв (суглинок, глина, чернозем, глинистый песок), представленных в [6], [8], [9].

Зависимость удельного сопротивления постоянному току материала провода от температуры обычно с достаточной точностью аппроксимируется линейной функцией [10]

               (1)

где – соответственно удельные сопротивления (в Ом∙м) провода при температурах ; α – температурный коэффициент сопротивления, принимаемый в наших экспериментах равным 0,004 1/˚ C. «Базовая» температура T₀ в нашем случае составляет 20˚C, а соответствующие значения  для фазных проводов и грозозащитных тросов приведены в [3, таблица 1] для первой ВЛЭП и в таблице 1 для второй ВЛЭП.

 

Таблица 2 – Рассмотренные режимы функционирования воздушных линий, определяющие вариацию их параметров

Примечание: * В этом случае учитываем дополнительный провес всех проводов, выбираемый из диапазона (0,5÷1) м.

 

Анализ зависимостей, представленных в [11], позволяет сделать вывод о том, что в отношении величины стрелы провеса провода также допустима линейная аппроксимация в функции температуры. При этом, обобщая графические данные из [11], [12], можно считать, что провес «фазы» в среднем увеличивается на 0,4 м при повышении температуры провода на 10˚ C (и, соответственно, уменьшается на 0,4 м при ее снижении на 10˚ C). Кроме того, как указано в [13], степень растяжения повивов из стали с увеличением температуры приблизительно вдвое меньше аналогичной для провода с повивами из алюминиевых проволок. Учитывая этот факт, а также то, что отношение сечения стали к сечению алюминиевой части существенно меньше для фазных проводов в сравнении с грозозащитными тросами, принимаем для последних изменение стрелы провеса в 0,2 м на каждые 10˚ C. Таким образом, с учетом выражения (2) в работе [3] можно записать следующие функциональные зависимости стрелы провеса от температуры:

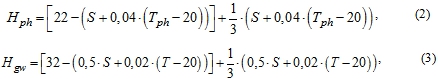
где  – средние высоты подвеса фазного провода и грозозащитного троса соответственно; S –  величина стрелы провеса фазного провода при 20˚C, принятая равной 9 м для двухцепной ВЛЭП и 11,1042 м для одноцепной ВЛЭП;  – температура фазного провода, определяемая ТОС и током по ВЛЭП; T – температура троса, определяемая атмосферными условиями. Нетрудно убедиться, что значения  при 20˚ C согласуются с данными, приведенными в [3, таблица 1] для первой ВЛЭП и в таблице 1 для второй ВЛЭП.

Вычислительные эксперименты выполнялись следующим образом. Для каждого из режимов, перечисленных в таблице 2, генерировалось случайным образом 10000 значений ТОС и 10000 величин удельного сопротивления грунта из соответствующих диапазонов для этих параметров, обозначенных в таблице 2. Для каждого сгенерированного значения ТОС по (1) рассчитывались удельные сопротивления фазного провода и грозозащитного троса, а по (2) и (3) – средние высоты подвеса проводов по трассе линии. При этом для режимов, характеризуемых большой загрузкой ВЛЭП, учитывался дополнительный нагрев «фазы» от протекающего тока, но не более чем на (10÷15)˚ C (конкретное значение выбиралось случайным образом). Это обосновано выполненными автором предварительными расчетами, свидетельствующими, что при наличии трех проводников в расщепленной фазе ([3, таблица 1]) может потребоваться ток порядка 1000 А для нагрева проводников на 10˚ C, а при токах в 600–700 А дополнительным нагревом (по отношению к ТОС) можно и вовсе пренебречь.

Результаты вычислительных экспериментов и выводы

По результатам экспериментов получено 10000 × 11 = 110000 значений для каждого из параметров ВЛЭП отдельных последовательностей, а затем определены отношения максимальных значений к соответствующим минимальным. Если все минимальные значения принять за «1», получаются гистограммы, изображенные на рисунках 2–5.

В отношении двухцепной линии (рисунки 2, 3) можно отметить, что наиболее сильные вариации были выявлены для активного сопротивления прямой последовательности (около 35 %) и индуктивного сопротивления, отражающего магнитную связь между двумя цепями ВЛЭП (около 27 %). В целом диапазоны изменения всех активных сопротивлений составляют как минимум 13 %, а вариации индуктивного сопротивления нулевой последовательности достигают 7 %.

Что касается моделируемой одноцепной ВЛЭП (рисунки 4, 5), были достигнуты очень существенные изменения всех сопротивлений, за исключением : рассчитанные максимальные отношения составили соответственно 35 % и 41 % для активных сопротивлений прямой и нулевой последовательностей, а вариации индуктивного сопротивления нулевой последовательности превысили 22 %.

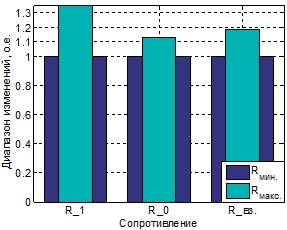
Рис. 2 – Диапазон возможных вариаций активных сопротивлений для ВЛЭП 500 кВ

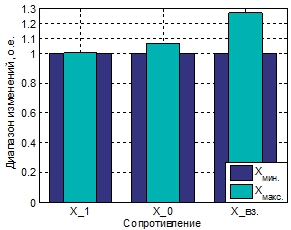
Рис. 3 – Диапазон возможных вариаций индуктивных сопротивлений для ВЛЭП 500 кВ

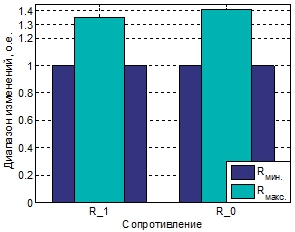
Рис. 4 – Диапазон возможных вариаций активных сопротивлений для ВЛЭП 345 кВ

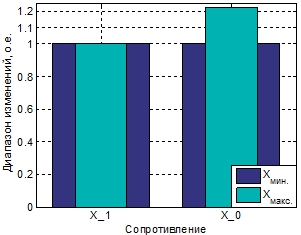
Рис. 5 – Диапазон возможных вариаций индуктивных сопротивлений для ВЛЭП 345 кВ

 

Что касается емкостных проводимостей, выявленные диапазоны их изменения для обеих ВЛЭП в целом меньше представленных на рисунках 2–5. Вариациями  можно пренебречь, а максимальные отношения значений  в обоих случаях немного превышают 3 %. Емкостная проводимость между двумя цепями ВЛЭП напряжением 500 кВ изменялась в ходе экспериментов почти на 12 %. Следует, однако, учитывать, что значения проводимостей могли варьироваться только за счет средних высот подвеса проводов, отклонения которых от «базовых» (указанных в [3, таблица 1] для первой ВЛЭП и в таблице 1 для второй ВЛЭП) определялись рассматриваемыми диапазонами температур (таблица 2), а также функциональными зависимостями (2) и (3). При этом в качестве «базовых» потенциально могли быть приняты совсем другие значения, поскольку маловероятно, что средние высоты подвеса проводов по трассе ВЛЭП могут быть известны с достаточной точностью. Поэтому возможный диапазон погрешностей в задании емкостных проводимостей шире по сравнению с достигнутым в ходе моделирования.

На основании полученных результатов можно заключить, что значения многих параметров ВЛЭП могут существенным образом варьироваться в зависимости от погодных условий и передаваемой по линии мощности. Данные, представленные на рисунках 2–5, в целом согласуются с оценками изменения параметров в других публикациях и свидетельствуют о необходимости уточнения фактических характеристик ВЛЭП.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Liao Y. Kezunovic M. Online optimal transmission line parameter estimation for relaying applications / Y. Liao, M. Kezunovic // IEEE Trans. Power Delivery. – January 2009. – Vol. 24, no. 1. – P. 96–102.
2. Shi D.. Identification of short transmission-line parameters from synchrophasor measurements / D. Shi, D.J. Tylavsky, N. Logic, K.M. Koellner // Proc. 40th North American Power Symposium (NAPS), Calgary, AB. – Canada, Sept. 28–30, 2008.
3. Иванов И. Е. Оценка влияния различных факторов на значения сопротивлений и проводимостей высоковольтной воздушной линии электропередачи / И. Е. Иванов // Вестник ИГЭУ. – 2017. – № 3. – С. 30-39.
4. Dommel H. W. Electromagnetic Transients Program (EMTP) Theory Book. – Portland, OR, USA: Bonneville Power Administration, 1986.
5. Martinez-Velasco J.A. Overhead lines / Martinez-Velasco J.A., Ramirez A.I., Davila M. // Power System Transients: Parameter Determination, J.A. Martinez-Velasco, Ed. – CRC Press, Taylor & Francis Group, 2009. – P. 17–135.
6. Нерпин С. В. Физика почвы / Нерпин С. В., Чудновский А.Ф.. – М.: Наука, 1967.
7. Higgs P. J. An investigation of earthing resistances / P. J. Higgs // Journal of the Institution of Electrical Engineers. – June 1930. – Vol. 68, no. 402. – P. 736–750.
8. ТарасовА., Цилько В. Гамма-съёмка. Новый метод оценки коррозионных свойств грунта на трассах ВЛ / А. Тарасов, В. Цилько // Новости электротехники. – 2005. – № 2 (32).
9. Peck R. B. Foundation engineering / Peck R. B., Hanson W. E., Thornburn T.H.. – John Wiley & Sons; 2 edition, 1974.
10. Bockarjova M., Andersson G. Transmission line conductor temperature impact on state estimation accuracy / M. Bockarjova, G. Andersson // Proc. 2007 IEEE Lausanne Powertech, Lausanne. – Switzerland, July 1-5, 2007.
11. Du Yan, Liao Y. Online estimation of power transmission line parameters, temperature and sag / Yan Du, Y Liao // Proc. 43rd North American Power Symposium (NAPS). – Boston, MA, USA, Aug. 4–6, 2011.
12. Slegers J. M. Design of resource to backbone transmission for a high wind penetration future (master’s thesis) / J. M. Slegers. – Iowa State University, 2013.
13. Douglass D. A. Sag and tension of conductor / D.A. Douglass, F.R. Thrash // Electric Power Generation, Transmission, and Distribution, 3rd ed., L.L. Grigsby, Ed. – CRC Press, Taylor & Francis Group, 2012.

Список литературы на английском языке / References in English

1. Liao Y., Kezunovic M. Online optimal transmission line parameter estimation for relaying applications / Y. Liao, M. Kezunovic // IEEE Trans. Power Delivery. – January 2009. – Vol. 24, no. 1. – P. 96–102.
2. Shi D. Identification of short transmission-line parameters from synchrophasor measurements / D. Shi, D.J. Tylavsky, N. Logic, K.M. Koellner // Proc. 40th North American Power Symposium (NAPS), Calgary, AB. – Canada, Sept. 28–30, 2008.
3. Ivanov I.E. Ocenka vliyaniya razlichnyh faktorov na znacheniya soprotivlenij i provodimostej vysokovol'tnoj vozdushnoj linii ehlektroperedachi [Investigation into the impact of various factors on the high voltage overhead transmission line impedances and admittances] / I.E. Ivanov // Vestnik IGEHU [Bulletin of ISPEU]. – 2017. – № 3. – P. 30-39. [in Russian]
4. Dommel H. W. Electromagnetic Transients Program (EMTP) Theory Book / H. W. Dommel. – Portland, OR, USA: Bonneville Power Administration, 1986.
5. Martinez-Velasco J.A. Overhead lines // Power System Transients: Parameter Determination, J.A. Martinez-Velasco, Ed. – CRC Press, Taylor & Francis Group, 2009. – P. 17–135.
6. Nerpin S.V., Chudnovskij A.F. Fizika pochvy [Soil Physics] / Nerpin S.V., Chudnovskij A.F.. – M.: Nauka, 1967. [in Russian]
7. Higgs P. J. An investigation of earthing resistances / P. J. Higgs // Journal of the Institution of Electrical Engineers. – June 1930. – Vol. 68, no. 402. – P. 736–750.
8. Tarasov A., Cil'ko V. Gamma-s"yomka. Novyj metod ocenki korrozionnyh svojstv grunta na trassah VL [Gamma survey. A new method of estimating the soil corrosive characteristics along the overhead line right-of-way] / A. Tarasov, V. Cil'ko // Novosti ehlektrotekhniki [Electrical Engineering News]. – 2005. – № 2 (32). [in Russian]
9. Peck R.B., Hanson W.E., Thornburn T.H. Foundation engineering. – John Wiley & Sons; 2 edition, 1974.
10. Bockarjova M., Andersson G. Transmission line conductor temperature impact on state estimation accuracy / M. Bockarjova, G. Andersson // Proc. 2007 IEEE Lausanne Powertech, Lausanne. – Switzerland, July 1-5, 2007.
11. Du Yan, Liao Y. Online estimation of power transmission line parameters, temperature and sag / Yan Du, Y Liao // Proc. 43rd North American Power Symposium (NAPS). – Boston, MA, USA, Aug. 4–6, 2011
12. Slegers J.M. Design of resource to backbone transmission for a high wind penetration future (master’s thesis) / J. M. Slegers. – Iowa State University, 2013
13. Douglass D.A. Sag and tension of conductor / D.A. Douglass, F.R. Thrash // Electric Power Generation, Transmission, and Distribution, 3rd ed., L.L. Grigsby, Ed. – CRC Press, Taylor & Francis Group, 2012.