ЗАДАЧА РАСПРОСТРАНЕНИЯ ТОНКОГО СЛОЯ ЖИДКОСТИ ПО НАКЛОННОЙ ПОВЕРХНОСТИ

Гильманов С.А.¹, Кильдибаева С.Р.² Ишмухаметова А.А.³

¹ORCID: 0000-0002-7562-784X, кандидат физико-математических наук,

²ORCID: 0000-0001-9586-8926, кандидат физико-математических наук,

³ORCID: 0000-0002-0575-0818, кандидат физико-математических наук,

Стерлитамакский филиал ФГБОУ ВО Башкирский государственный университет

Работа выполнена при поддержке гранта СФ БашГУ № В17-63

ЗАДАЧА РАСПРОСТРАНЕНИЯ ТОНКОГО СЛОЯ ЖИДКОСТИ ПО НАКЛОННОЙ ПОВЕРХНОСТИ

Аннотация

В работе проведен анализ некоторых особенностей движения тонкого слоя невязкой несжимаемой жидкости, стекающей по наклонной поверхности в приближении теории "мелкой воды". На основе предложенного подхода изучено влияние угла наклона поверхности на динамику движения флюида. Для упрощения процесса получения решений введена обобщенная автомодельная схема, когда вид временного компонента принимается без уточнений. Предложенная подстановка позволяет получить в ряде частных случаев аналитические решения. Выбор слагаемых уравнения для преобразования дает возможность получения достаточно большого количества разных решений в зависимости от количества слагаемых в уравнении. Сравнение с приближенными решениями может быть использовано для определения диапазона изменения особых параметров, получаемых при использовании метода. Полученные результаты могут представлять интерес, например, при подборе угла наклона стенок канавы, перехватывающей дождевую воду, стекающую с холма на дорогу или с полотна дороги в канаву.

Ключевые слова: тонкий слой жидкости, угол наклона, мелкая вода, несжимаемая жидкость, невязкая жидкость.

Gilmanov S.A.¹, Kildibaeva S.R.² Ishmukhametova A.A.³

¹ORCID: 0000-0002-7562-784X, PhD in Physics and Mathematics,

²ORCID: 0000-0001-9586-8926, PhD in Physics and Mathematics,

³ORCID: 0000-0002-0575-0818, PhD in Physics and Mathematics,

Sterlitamak Branch of FSBEI of Higher Education Bashkir State University

The work was supported by the Bashkir State University grant No.B17-6

PROBLEM OF THIN LIQUID LAYER DISTRIBUTION ON ANGLED SURFACE

Abstract

The article analyzes some features of the thin layer motion of inviscid incompressible fluid flowing along an inclined surface in the approximation of the theory of “shallow water.” Based on the proposed approach, we studied the influence of the surface inclination angle on fluid dynamics. To simplify the process of obtaining solutions, a generalized self-similar scheme is introduced, when the form of the time component is adopted without specification. Proposed substitution allows us to obtain analytical solutions in a number of special cases. The choice of the terms of the equation for the transformation enables obtaining a sufficiently large number of different solutions depending on the number of terms in the equation. Comparison with approximate solutions can be used to determine the range of variation of the special parameters obtained by using the method. The results obtained may be of interest, for example, in selecting the angle of inclination of the walls of the ditch, intercepting rainwater flowing from the hill to the road or from the roadway to the ditch.

Keywords: thin layer of liquid, angle of inclination, shallow water, incompressible fluid, non-viscous liquid.

Поток жидкости, у которого линейные размеры вдоль поверхности грунта значительно больше, чем толщина (кратчайшее расстояние от поверхности грунта до свободной границы с атмосферой) могут быть описаны на основе теории «мелкой воды». Эволюция потоков, описываемых уравнениями из этой теории, для частных случаев приведена в [2, С. 65], [3, C. 82], [5, C. 90]. Так же некоторые особенности рассмотрены в работах [6, С. 520], [7, С. 106], [10, С. 137]

Рассмотрим поток жидкости, стекающий по наклонной поверхности с углом . На поток действуют силы тяжести и трения со стороны окружающей среды. Причем с ростом угла наклона влияние силы тяжести меняется нелинейно Жидкость считается невязкой и несжимаемой, ее испарением в рамках представленной постановки можно пренебречь. Ось абсцисс 0х направлена вдоль наклонной поверхности. Ось 0n направлена перпендикулярно оси 0х. Скорость потока направлена вдоль оси 0х. Схема потока представлена на рис. 1.

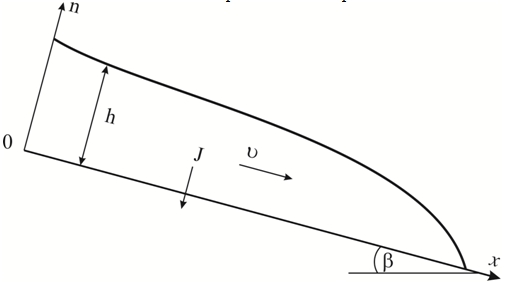
Рис. 1.– Схема одномерного потока тонкого слоя жидкости вдоль наклонной поверхности

Математическая модель, аналогично принятой в [1, С. 174], [8, C. 610], [9, C. 89] для гидродинамической задачи может быть записана как система уравнений балансов объема и локального количества движения. Такая постановка позволяет моделировать эволюции изотермической жидкости.

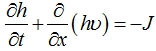                                                            (1)

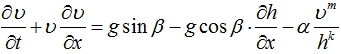            (2)

Здесь h, υ – высота и усредненная по высоте скорость потока в направлении, параллельном наклонной поверхности, t, x – время и координата, g – ускорение сил тяжести, J – интенсивность потерь массы на единицу длины поверхности грунта за счет впитывания, α, m, k – эмпирические параметры.

Применительно для источника, у которого высота жидкости в начале координат поддерживается постоянной, система уравнений (1) – (2) замыкается следующим набором краевых условий:

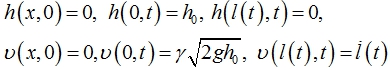 (3)

Конкретная физическая интерпретация может быть представлена в виде области пространства, ограниченного непроницаемой преградой, например шлюз в реке. Здесь l(t) – величина, указывающая положение переднего края потока в текущий момент времени. Коэффициент γ в формуле Торричелли для граничного условия в начале координат при определении скорости возникает при усреднении скорости по высоте. Учет сопротивления рассмотрен на базе альтернативного подхода. Из начальных условий получаем l(0) = 0.

Для получения решения системы уравнений (1) – (2) с краевыми условиями (3) введем замену переменных следующим образом

  (4)

Величину ξ назовем автомодельной переменной. Она является безразмерной. В дальнейшем для упрощения записей аргументы функций a(t), b(t), H(ξ), V(ξ) опустим.

С учетом приведенной замены переменных (4) система уравнений (1) – (2) примет вид:

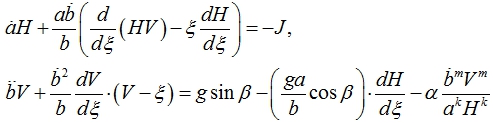     (5)

Сведем уравнения в (5) к такому виду, чтобы с одной стороны от равенства была функция от t, а с другой – от ξ. Первое уравнение в (5) преобразуем следующим образом.

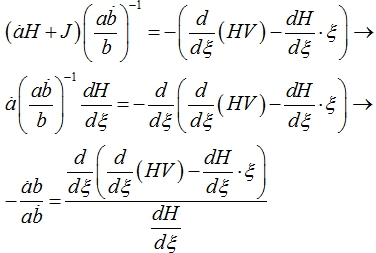       (6)

Полученное уравнение является тождеством. Обозначим его через  параметр Р и перепишем отдельно временное и автомодельное уравнения. Для обоих уравнений укажем общее решение. В силу линейности полученного уравнения имеет место следующая цепочка элементарных преобразований

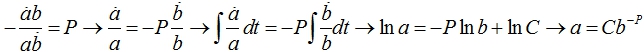 (7)

Полученное решение связывает приведенные длину и высоту потока. В данном случае для объема жидкости имеет место обратная пропорциональность этих параметров, рост высоты сопровождается уменьшением длины, справедливо и обратное. С ростом размерности общая зависимость остается справедливой, меняется только значение параметра Р.

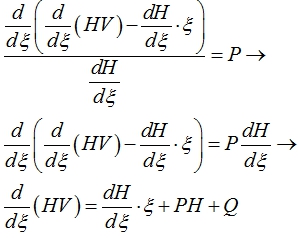                     (8)

При значении параметра Р = 1  имеем аналитическое решение вида

                   (9)

Решения (7) и (9) включают в себя по две функции, для уточнения решений рассмотрим второе уравнение из (5). Это уравнение имеет пять слагаемых с различными множителями относительно автомодельной и временной переменных, что дает более 20 вариантов ее преобразования. Рассмотрим один из возможных вариантов. Продифференцировав второе уравнение (5) по ξ, получим:

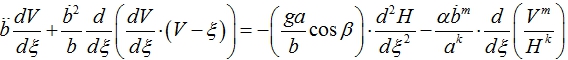   (10)

Далее умножаем (10) на  и продифференцируем полученное уравнение по времени. Результат запишем как

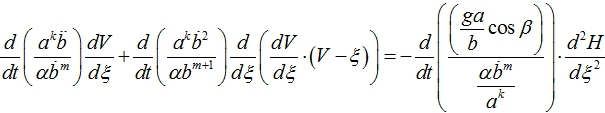     (11)

Умножаем (11) на 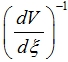, затем осуществляем дифференцирование по автомодельной переменной ξ , сводя (11) к виду 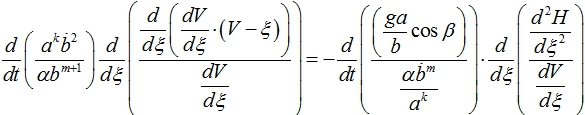(12)

             (12)

Преобразуем (12) так, чтобы слева от знака равенства была функция времени, а справа – функция автомодельной переменной, тогда (13) будет тождеством согласно [4, С. 369], так как его левая сторона зависит от t, а правая – от ξ.

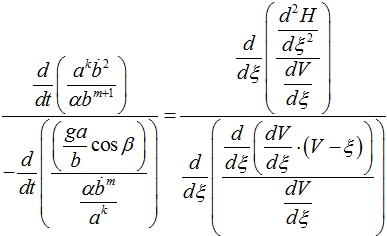                   (13)

Полученное тождество преобразуем аналогично (6). Введем параметр T. Тогда временная часть уравнения может быть записана как

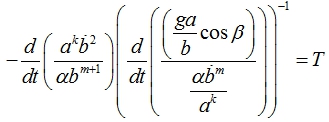            (14)

После преобразования (14), интегрирования по времени и дополнительного преобразования получим

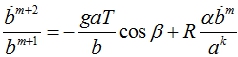        (15)

Подстановка вместо функции a из (7) дает обыкновенное дифференциальное уравнение для функции b.

                   (16)

Обычно силы сопротивления со стороны окружающей среды принято брать пропорционально скорости (для медленных течений) или квадрату скорости (для быстрых течений). Учитывая, что при P=1 существует аналитическое решение для автомодельного уравнения, получим при m=1

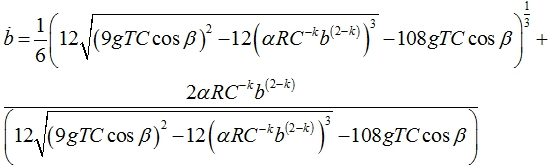             (17)

и m=2 соответственно

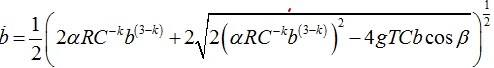                 (18)

Тестовые решения при T=–1, C=1, R=–1, k=0, α=1, g=9.81, b(0)=0,  имеют вид, указанный на рисунке. Эти решения указывают на рост длины разлива с течением времени. Поиск зависимости решения от параметра  указал на слабую зависимость решения от параметра при малых углах наклона. По – видимому, это связано с тем, что при малых углах наклона имеет место линейная зависимость между углом β и долей силы тяжести, ответственной за стремление к уменьшению величины свободной поверхности потока.

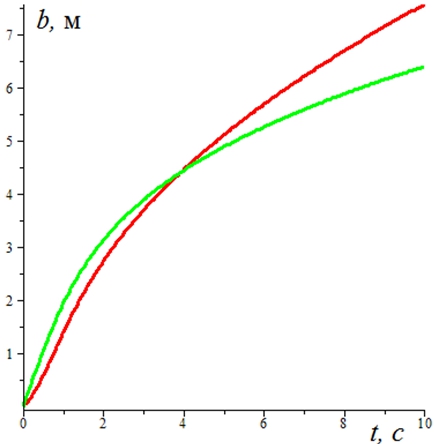
Рис. 2. – Зависимость длины потока от времени при разных значениях параметра m.

Красная линия – m=2, зеленая – m=1. Зная зависимость b(t) от времени, на основе (7) можно получить зависимость a(t). Т.е., формально временная часть уравнения решена.

Далее рассмотрим правую часть (13) в виде, аналогичном (14).

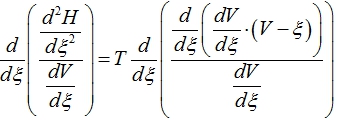                (19)

Проинтегрировав (19) по ξ и умножив на , получим

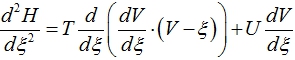                        (20)

Повторное интегрирование дает

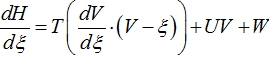                         (21)

Выразив из (9) Н и подставив его в (21) получим обыкновенное дифференциальное уравнение для функции V.

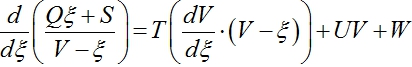                                         (22)

Это уравнение имеет аналитические решения при некоторых частных значениях параметров Q, S, U, W. Например, при Q=1, S=1, U=1, T=–1 имеет место аналитическое решение.

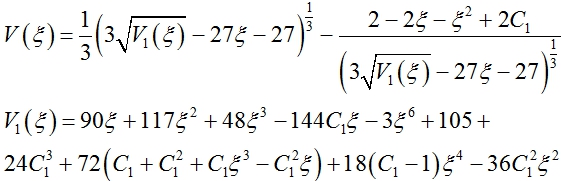          (23)

Анализ показывает, что начальное значение V будет положительным при C1 < –2.5 и отрицательным при C1 > – 1. Тогда функция H  имеет вид

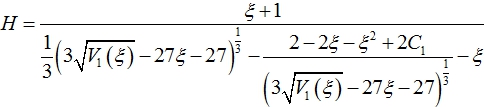                                       (24)

В работе рассмотрена математическая модель растекания жидкости вдоль наклонной поверхности с учетом сил сопротивления в степенной форме. Получены автомодельные аналитические и численные временные решения. Полученные решения проанализированы с учетом варьирования угла наклона и вида слагаемого, ответственного за учет взаимодействия с окружающей средой. Проанализирован диапазон константы интегрирования в решении (23). Установлены интервалы, где решение отсутствует, где начальное значение V(0) положительно при указанных значениях параметров. На основе полученных решений может быть построена реальная динамика жидкости вдоль наклонной поверхности.

Для обобщения результатов частные численные решения представленных дифференциальных уравнений могут быть аппроксимированы на основе точечного квадратичного приближения, что позволяет для конкретного набора параметров и граничных условий получить полностью аналитическое решение с погрешностями в наперед заданном диапазоне.

Список литературы / References

1. Гильманов С.А., Ишмухаметова А.А. Моделирование разливов нефти при разрушении трубопровода в процессе транспортировки // Альтернативные источники энергии в транспортно-технологическом комплексе: проблемы и перспективы рационального использования. 2015. – Т.2, № 1. – С. 174–177.
2. Залипаева О.А., Трусов А.С. Растекание жидкости по горизонтальной поверхности // Известия Волгоградского государственного технического университета. –2012. – Т.5, № 1 (88). – С. 65–67.
3. Коханенко В.Н., Мицик М.Ф., Алейникова О.А. О плановой задаче растекания бурного потока несжимаемой жидкости // Известия высших учебных заведений. Северо–Кавказский регион. Серия: Технические науки. –2012. – № 6, – С. 82–88.
4. Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.–13-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1985. – 560 с.
5. Пономарева М.А., Шрагер Г.Р., Якутенок В.А. Использование уравнения Дюпре - Юнга для решения задачи о растекании жидкости при ограниченном смачивании//Вестник Томского государственного университета. Математика и механика. – 2008. – № 1. – С. 90–96.
6. Свиркунов П.Н. Неустановившиеся осесимметричные движения в приближении теории мелкой воды // ПММ. – 1996. –Т.60, № 3. – С.520–522.
7. Татосов А. В. Растекание жидкости во влажной пористой среде // Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика, – 2012. – № 4. – С. 104–109.
8. Shagapov V.S., Gil’manov S.A. A contribution to the theory of spreading of liquid-containing ejections over a horizontal surface // Journal of Engineering Physics and Thermophysics. – 2015. – Vol. 88. – № 3. – P. 630–644.
9. Shagapov V.S., Gils'manov S.A. Spreading of the liquid over the surface with penetration into the soil // Journal of Applied Mechanics and Technical Physics. – 2010. – Vol. 51. – № 5. – P. 88–94.
10. Spannuth M. J., Neufeld J. A., Wettlaufer J. S., Grae Worster M. Axisymmetric viscous gravity currents flowing over a porous medium // J. Fluid Mech., – 2009. Vol. 622. – №1. –P. 135–144.

Список литературы на английском языке / References in English

1. Gil'manov S.A., Ishmuhametova A.A. Modelirovanie razlivov nefti pri razrushenii truboprovoda v processe transportirovki [Oil spills modeling during the pipeline destruction in transportation process] // Al'ternativnye istochniki jenergii v transportno-tehnologicheskom komplekse: problemy i perspektivy racional'nogo ispol'zovanija [Alternative energy sources in the transport-technological complex: problems and prospects of rational using]. –2015. – Vol.2. – № 1. – P. 174–177. [in Russian]
2. Zalipaeva O.A., Trusov A.S. Rastekanie zhidkosti po gorizontal'noj poverhnosti [The liquid spreading by horizontal surface] // Izvestija Volgogradskogo gosudarstvennogo tehnicheskogo universiteta [The news of Volgograd state technical University]. –2012.– Vol.5. – № 1 (88). – P. 65 – 67. [in Russian]
3. Kohanenko V.N., Micik M.F., Alejnikova O.A. O planovoj zadache rastekanija burnogo potoka neszhimaemoj zhidkosti [About the planned task turbulent flow of incompressible fluid] // Izvestija vysshih uchebnyh zavedenij. Severo–Kavkazskij region. Serija: Tehnicheskie nauki [News of higher educational institutions. The North Caucasus region. Series: Technical Sciences].– 2012. – № 6. – P. 82 – 88. [in Russian]
4. Piskunov N. S. Differencial'noe i integral'noe ischislenija dlja vtuzov, t. 2: Uchebnoe posobie dlja vtuzov [Differential and integral calculus for technical colleges, Vol. 2: Textbook for technical colleges]. – 13th iss. – M.: Nauka, Glavnaja redakcija fiziko-matematicheskoj literatury [М.: Science, General edition physical and mathematical literature], 1985. – 560 p. [in Russian]
5. Ponomareva M.A., Shrager G.R., Jakutenok V.A. Ispol'zovanie uravnenija Djupre - Junga dlja reshenija zadachi o rastekanii zhidkosti pri ogranichennom smachivanii [Usage of the equation of Dupre - Yung for the solution of tasks about spreading of the liquid at a limited wetting] // Vestnik Tomskogo gosudarstvennogo universiteta. Matematika i mehanika. [Bulletin of the Tomsk state University. Mathematics and mechanics]. – 2008. – № 1. – P. 90 – 96. [in Russian]
6. Svirkunov P.N. Neustanovivshiesja osesimmetrichnye dvizhenija v priblizhenii teorii melkoj vody [Unsteady axisymmetric motion in the approximation of shallow water theory] // PMM [Journal of Applied Mathematics and Mechanics]. – 1996. – V.60. – № 3. – P.520 – 522. [in Russian]
7. Tatosov A. V. Rastekanie zhidkosti vo vlazhnoj poristoj srede [Spreading the liquid in a wet porous medium] // Vestnik Tjumenskogo gosudarstvennogo universiteta. Fiziko-matematicheskoe modelirovanie. Neft', gaz, jenergetika [Herald of Tyumen state University. Physico-mathematical modeling. Oil, gas, energy], – 2012. – № 4. – P. 104 – 109. [in Russian]
8. Shagapov V.S., Gil’manov S.A. A contribution to the theory of spreading of liquid-containing ejections over a horizontal surface // Journal of Engineering Physics and Thermophysics. – 2015. – Vol. 88. – № 3. – P. 630–644.
9. Shagapov V.S., Gils'manov S.A. Spreading of the liquid over the surface with penetration into the soil // Journal of Applied Mechanics and Technical Physics. – 2010. – Vol. 51. – № 5. – P. 88–94.
10. Spannuth M. J., Neufeld J. A., Wettlaufer J. S., Grae Worster M. Axisymmetric viscous gravity currents flowing over a porous medium // J. Fluid Mech., – 2009. Vol. 622. – №1. –P. 135–144.