РАСЧЕТНАЯ МОДЕЛЬ ПОТЕНЦИАЛЬНЫХ ЗОН РАЗРУШЕНИЯ НЕСУЩИХ КОНСТРУКЦИЙ МЕТАЛЛУРГИЧЕСКИХ КРАНОВ

Извеков Ю.А.¹, Гугина Е.М.²

¹ORCID: 0000-0002-1892-4055, кандидат технических наук, доцент, ²Кандидат педагогических наук,

Магнитогорский государственный технический университет им. Г.И. Носова

РАСЧЕТНАЯ МОДЕЛЬ ПОТЕНЦИАЛЬНЫХ ЗОН РАЗРУШЕНИЯ НЕСУЩИХ КОНСТРУКЦИЙ МЕТАЛЛУРГИЧЕСКИХ КРАНОВ

Аннотация

Представляется актуальным разработка и создание согласованных по целям и задачам отдельных моделей конструкционного риска. Структура таких моделей предполагает разложение R-характеристик. Описана концептуальная расчетная модель потенциальных зон разрушения несущих конструкций металлургических мостовых кранов. Определены задачи для корректного описания такой модели. Предложенные теоретические модели могут быть использованы в решении практических задач конструкционного риск-анализа такой  группы объектов как специальные тяжелые металлургические мостовые краны.

Ключевые слова: конструкционный риск-анализ, технический риск, несущие конструкции, потенциальные зоны разрушения, металлургические мостовые краны, сложная техническая система.

 Izvekov Yu.A.¹, Gugina E.M.²

¹ORCID: 0000-0002-1892-4055, PhD in Engineering, Associate professor, ²PhD in Pedagogy,

Magnitogorsk State Technical University named after G.I. Nosova

DESIGN MODEL OF POTENTIAL DESTRUCTION ZONES OF METALLURGICAL CRANES BEARING STRUCTURES

Abstract

Development and creation of individual models of structural risk agreed by the purposes and tasks are topical. The structure of such models implies the decomposition of R-characteristics. The conceptual design model of potential destruction zones of metal bridge cranes bearing structures is described. The problems for the correct description of such a model are determined. The proposed theoretical models can be used in solving practical problems of structural risk analysis of such a group of objects as special heavy metallurgical bridge cranes.

Keywords: structural risk analysis, technical risk, load-bearing structures, potential destruction zones, metallurgical bridge cranes, complex technical system.

На сегодняшний день предствляется проблематичным и маловероятным построение всеобъемлющей модели конструкционного риска. Актуальным представляется разработка и создание согласованных по целям и задачам отдельных моделей конструкционного риска [1, С. 522], [5, С. 265]. Структура таких моделей предполагает разложение R-характеристик по следующей форме [1, C. 524]:

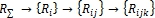   (1)

где 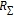 - конструкционный риск;  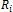- подсистемный риск;  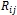– элементный риск;  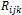- критериальный риск.

Решением такого разложения будет критериальный риск – как вероятность ущерба W, связанного непосредственно с разрушением конструкции по заданному виду предельного состояния:

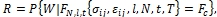   (2)

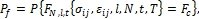где       (3)

Точное решение разложения (1) найти пока не представляется возможным, так как наносимый разрушениями ущерб определяется конкретными схемами повреждений структуры различных конструкций.

Расcмотрим конструкционный риск-анализ таких сложных технических систем  как краны литейные (миксерные, заливочные, разливочные) – краны мостового типа, обрудованные механизмами подъема и опрокидывания литейного ковша, предназначенные для разливки и заливки жидкого металла. Механизм главного подъема имеет два привода, соединенные между собой кинематически и имеющих храповые передачи для возможности работы одного привода при аварийной остановке другого.

Опишем конструкцию таких кранов исходя из позиций целостности и иерархичности. Выделим в конструкции расматриваемых кранов два уровня: на первом разделим конструкцию на блоки, локальные по множествку критериальных функций; на втором – выделим блоки, локальные по множеству варьируемых параметров, определяющих критериальные функции.

Подсистема 1 – металлоконструкция моста: пролетные и концевые балки главного и вспомогательного мостов; зоны приварки кронштейнов проходных галерей моста к стенкам балок; нижние пояса балок;

 подсистема 2 – пролетные балки вспомогательного моста: общие деформации балок; местные деформации нижних поясов;

подсистема 3 – траверса механизма главного подъема: крюки; металлоконструкция траверсы;

подсистема 4 – храповая передача механизма главного подъема: храповое колесо; собачки; оси крепления собачек; прижимные пружины; осевое крепление храпового колеса.

Таким образом, имеем 4 блока (подсистемы) первого уровня и десять элементов второго уровня.

Будем рассматривать два крайних случая: суммирование ущербов и умножение ущербов в процессе эскалации повреждений.

Коэффициенты а представляют собой веса значимости всех подсистем и элементов конструкции, они должны удовлетворять следующим условиям:

Для рассматриваемой группы конструкций будем учитывать следующее:

- анализу подвергаются маловероятные события;

-  большая неопределенность, обусловленная случайным характером внешних воздействий и процессов в элементах конструкций, а также отсутствие четких целей и критериев безопасности;

- ограниченность во времени – на стадии проектирования – срок проекта, на стадии эксплуатации – время реагирования на чрезвычайную или аварийную ситуацию.

Будем считать все четыре подсистемы потенциальными зонами разрушения :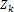

Тогда, с учетом (7) критериальную функцию риска можно представить в виде:

Таким образом, достаточно исследовать вариации 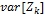 состояний этих четырех потенциальных зон разрушения и определить вероятности выхода этих вариаций из области безопасности 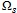. Это позволяет нам снизить размерность задачи конструкционного риск-анализа.

Сформируем базовую параметрическую модель, основываясь на аппарате механики разрушения [1, C. 524], [5, C. 264]. При построении параметрической модели зоны 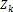 в общем случае возникают три задачи.

Первая задача – определение характера нагрузки, действующий на элемнт конструкции, примем 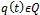, так как нагрузка является внешним параметром.

Вторая задача – выбор модели дефекта, определяющая его тип, вид и размеры. Можно предположить [1, С. 531], что практический интерес для конструкционного риск-анализа представляют полуэллиптические и эллиптические трещины, которые по размерам могут быть сопоставимы с размерами элемнтов самой конструкции. Другие дефекты в процессе эксплуатации выявляются и устраняются. Определяемые виды и размеры дефектов могут быть приняты к расчетам при использовании методических указаний по обследованию специальных металлургических кранов РД 10-112-6-03.

Третья задача – выбор уравнения состояния потенциальной зоны разрушения 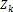. Для этого выделим в элементе конструкции некоторый объем, соответствующий зоне разрушения. Входные параметры – напряжения  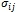и   деформации  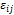[3, С. 32] от нагрузки q(t); размеры дефекта  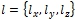Выходные параметры – силовые, деформационные и энергетические характеристики напряженно-деформированного состояния в области вершины дефекта.

Для описания полей напряжений и деформаций будем использовать энергетический подход. После соответствующего интегрирования по объему V произведение  приводит к конечной энергии деформации, которая характеризуется J- интегралом. На основании HRR-решения напряжения и деформации запишем:

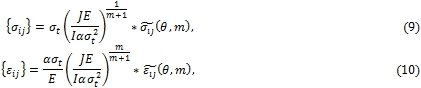
где 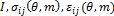 - безразмерные функции;  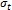- предел текучести; a,m - параметры диаграммы деформирования; J – энергетический контурный интеграл. В таком случае критериальное условие предельного состояния будет:

где 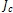  - критическое значение J-интеграла.

Преимуществом J-интеграла является его выражение через коэффициенты интенсивности напряжений и сохранение инвариантности при упругом и упругопластичесеком деформировании, а также учет стадии стабильного подрастания трещины до наступления критического состояния.

Таким образом, для правильного описания потенциальной зоны разрушения необходимо:

- определить вид и размеры дефекта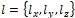 

- определить поля напряжени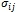й  при 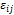 заданной нагрузке q(t);

- с учетом сингулярности выбрать уравнения состояния и определить коэффициенты интенсивности напряжений 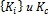, коэффициенты интенсивности деформаций 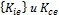, энергетические характеристики .

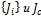Кроме этого, полученная расчетная (теоретическая) модель потенциальных зон разрушения несущих конструкций металлургических кранов позволит развить дальше методологию конструкционного риска и провести расчеты с целью построения норм рисков для определенного класса оборудования. Это позволит существенно влиять на обеспечение техногенной безопасности и управление ею, прогнозирование изменений механических характеристик материала конструкции на всех этапах жизненного цикла.

 

Список литературы / References

1. Безопасность России. Правовые, социально-экономические и научно-технические аспекты. Анализ риска и проблем безопасности. В 4-х частях. // Ч.1. Основы анализа и регулирования безопасности: Научн. руковод. К.В. Фролов. – М.: МГФ «Знание», 2006. – 640 с: ил.
2. Бархоткин В.В., Извеков Ю.А., Миникаев С.Р. Обзор аварий на крановом оборудовании металлургических производств // Международный журнал прикладных и фундаментальных исследований. – 2013. – № 10(1). – стр.9-11.URL: www.rae.ru/upfs/?section=content&op=show_article&article_id=4040 (дата обращения: 10.11.2017).
3. Бирюков М.П. Динамика и прогнозирующий расчет механических систем. “Вышэйшая школа”, Минск, 1980. – 192 с: ил.
4. Гилмор Р. Прикладная теория катастроф: в 2 т //М, Мир. – 1984.
5. Извеков Ю.А., Кобелькова Е.В., Лосева Н.А. Анализ динамики и вопросы оптимизации металлургических мостовых кранов // Фундаментальные исследования. – 2013. – № 6 (2). – стр. 263-266. URL: www.rae.ru/fs/?section=content&op=show_article&article_id=10000704 (дата обращения: 01.11.2017).
6. Крылова Е.А., Извеков Ю.А. О подходе к оценке техногенной безопасности металлургического производства // Успехи современного естествознания. – 2012. – № 6 – С. 32-33. URL: www.rae.ru/use/?section=content&op=show_article&article_id=9999573 (дата обращения: 01.11.2017).
7. Kumamoto, H. and E.J. Henley, 1996. Probabilistic Risk Assessment and Management for Engineers and Scientists. Second Edition. New York: IEEE Press, pp: 598.
8. Taguchi, G., (1985). «Quality Engineering in Japan», Bulletin of the Japan Society of Precision Engineering, Vol 19 No (4), pp: 237-242.
9. Boulding, K.E., 1956. General Systems Theory – The Skeleton of Science. Management Science, 2: 197-208.
10. Sorensen Arthur Gr. A statistical analysis of product reliability due to random vibration. Proc. Ann. Reliab. AndMaint. Symp. – Philadelphia, 1973.

Список литературы на английском языке / References in English

1. Bezopasnost' Rossii. Pravovye, social'no-jekonomicheskie i nauchno-tehnicheskie aspekty. Analiz riska i problem bezopasnosti. V 4-h chastjah [Security of Russia. Legal, Social an Economic, Scientific and Technical Aspects. Risk and Security Analysis. In 4 Parts.] // Ch.1. Osnovy analiza i regulirovanija bezopasnosti [P.1. Fundamentals of Safety Analysis and Regulation: Sc. leadership]: Nauchn. rukovod. K.V. Frolov. – M.: MGF «Znanie», 2006. – 640 p.: il. [in Russian]
2. Barhotkin V.V. Obzor avarij na kranovom oborudovanii metallurgicheskih proizvodstv [Overview of Accidents at Crane Equipment of Metallurgical Industries] / V.V. Barhotkin, Ju.A. Izvekov, S.R. Minikaev // International Journal of Applied and Fundamental Research] [Electronic resource. – 2013. – No. 10(1). – P. 9-11. URL: www.rae.ru/upfs/?section=content&op=show_article&article_id=4040 (Reference date: 10.11.2017). [in Russian]
3. Birjukov M.P. Dinamika i prognozirujushhij raschet mehanicheskih system [Dynamics and predictive calculation of mechanical systems]. Minsk: “Vyshjejshaja shkola”, 1980. – 192 p.: il. [in Russian]
4. Gilmor R. Prikladnaja teorija katastrof: v 2 t [Applied theory of catastrophes: in 2 volumes]. – M.: Mir. – 1984. [in Russian]
5. Izvekov Ju.A. Analiz dinamiki i voprosy optimizacii metallurgicheskih mostovyh kranov [Analysis of dynamics and optimization of metallurgical bridge cranes] / Ju.A. Izvekov, E.V. Kobel'kova, N.A. Loseva // Fundamental research [Electronic resource]. – 2013. – No. 6 (2). – P. 263-266. URL: www.rae.ru/fs/?section=content&op=show_article&article_id=10000704 (Reference date: 01.11.2017). [in Russian]
6. Krylova E.A. O podhode k ocenke tehnogennoj bezopasnosti metallurgicheskogo proizvodstva [About the Approach to the Assessment of the Technogenic Safety of Metallurgical Production] / E.A. Krylova, Ju.A. Izvekov // Successes of modern natural science [Electronic resource]. – 2012. – No. 6 – P. 32-33. URL: www.rae.ru/use/?section=content&op=show_article&article_id=9999573 (Reference date: 01.11.2017). [in Russian]
7. Kumamoto H. Probabilistic Risk Assessment and Management for Engineers and Scientists. Second Edition / H. Kumamoto, E.J. Henley. – 1996. – New York: IEEE Press. – 598 p.
8. Taguchi G. Quality Engineering in Japan // Bulletin of the Japan Society of Precision Engineering. – 1985. – Vol 19, No (4), Р.: 237-242.
9. Boulding K.E. General Systems Theory – The Skeleton of Science. Management Science. – 1956. – Р. 197-208.
10. Sorensen A.G. A statistical analysis of product reliability due to random vibration // Proc. Ann. Reliab. AndMaint. Symp. – Philadelphia, 1973