МУЛЬТИФРАКТАЛЬНАЯ СЕГМЕНТАЦИЯ ЛАНДШАФТОВ НА КОСМИЧЕСКОМ ИЗОБРАЖЕНИИ

Бутусов О.Б.¹, Редикульцева Н.И.², Никифорова О.П.³

¹ORCID: 0000-0003-1361-2121, профессор, доктор физико-математических наук,

Московский политехнический университет, Московский гуманитарный университет,

Российский химико-технологический университет им. Д.И. Менделеева;

²доцент, кандидат технических наук, Московский гуманитарный университет;

³кандидат технических наук, Государственный университет управления

МУЛЬТИФРАКТАЛЬНАЯ СЕГМЕНТАЦИЯ ЛАНДШАФТОВ НА КОСМИЧЕСКОМ ИЗОБРАЖЕНИИ

Аннотация

Проведен мультифрактальный анализ двух фрагментов космического снимка земной поверхности в районе Центрального лесного заповедника со спутника Landsat7 (четвертый спектральный канал). Первый фрагмент – это изображение лесного ландшафта, второй – сельскохозяйственного. В результате мультифрактального анализа рассчитаны экспоненты Холдера для двух показателей: iso-мера и s-мера. Экспоненты Холдера использованы для расчета мультифрактальных спектров и обобщенных фрактальных размерностей. Установлено, что наилучшим критерием для сегментации ландшафтов является корреляционная размерность. Проведено исследование возможности применения для сегментации ландшафтов квантования α-изображений. В результате установлено, что экспонента Холдера хорошо выделяет границы между нечеткими объектами на космическом изображении.

Ключевые слова: космические снимки, мультифрактальный анализ, экспонента Холдера, обобщенные фрактальные размерности, корреляционная размерность, квантование изображений.

Butusov O.B.¹, Redikultseva N.I.², Nikiforova O.P.³

¹ORCID: 0000-0003-1361-2121, Professor, PhD in Physics and Mathematics,

Moscow Polytechnic University, Moscow University for Humanities, D. Mendeleev University of Chemical Technology of Russia;

²Associate professor, PhD in Engineering, Moscow University for Humanities;

³PhD in Engineering, State University of Management

MULTIFRACTAL SEGMENTATION OF LANDSCAPES ON SPACE IMAGE

Abstract

A multifractal analysis of two segments of the space image of the Earth surface in the area of the Central Forest Reserve from the Landsat7 satellite (the fourth spectral channel) is carried out. The first segment is an image of a forest landscape, and the second one is an agricultural area. As a result of multifractal analysis, Holder exponents are calculated for two indicators: iso-measure and s-measure. Holder exponents are used to calculate multifractal spectra and generalized fractal dimensions. It is found that the best criterion for segmentation of landscapes is the correlation dimension. A study of the possible application of α-image quantization for segmentation of landscapes is carried out. As a result, it is established that the Holder exponent clearly distinguishes between the fuzzy objects in the space image.

Keywords: space images, multifractal analysis, Holder exponent, generalized fractal dimensions, correlation dimension, image quantization.

Введение. Известно [1], [2], что достаточно большое количество природных объектов имеют фрактальную природу, которая частично проявляется на изображениях этих объектов. При изучении фрактальных объектов в качестве одного из основных показателей фрактальности часто используются мультифрактальные спектры [1], [3], которые достаточно хорошо описывает структурные особенности природных фракталов, например, микроструктуры наноматериалов [4] или кластерную структуру ландшафтов на спутниковых снимках [5], [6]. Как правило, природные фракталы характеризуются целым спектром различных фрактальных размерностей [7], [8], [9]. Такие фракталы получили название мультифракталов [1], [3]. В настоящее время фрактальный анализ широко применяется в различных областях науки и техники, таких как материаловедение [10], медицина [11], [12], исследование Земли с помощью космических снимков [5], [6] и пр. Фрактальная размерность многих материалов успешно используется при их изучении по микрофотографиям [4]. Также фрактальная размерность изображений с успехом применяется в медицинской диагностике [11], [12], [13], когда традиционные методы анализа изображений оказываются бессильны. Фрактальный анализ хорошо зарекомендовал себя при изучении фрактальных свойств природных объектов и ландшафтов [5] ,[6]. Измеряя фрактальную размерность на различных участках спутниковых изображений, можно проводить фрактальную сегментацию этих изображений и тем самым выделять природные объекты, фрактальная структура которых различна.

Цель данной работы изучение возможности использования обобщенных фрактальных размерностей для фрактальной сегментации ландшафтов на космических изображениях природных объектов.

Методика. В настоящее время для расчета фрактальной размерности в основном применяются следующие методы [1], [2], [3].

Первый метод основан на непосредственном использовании формулы фрактальной размерности Минковского, совпадающей в большинстве случаев с размерностью Хаусдорфа и имеющей следующий вид [1], [2], [3]

                                                                                  (1)

где N(a) – количество квадратов, покрывающих объект, , s – длина стороны квадрата. Расчет проводится для фиксированных или скользящих окон на изображении.

Второй метод основан на выделении границ объектов и последующего применения алгоритмов “box counting” (ВС) или «кронциркуля» [1], [2], [3]. Скользящее окно покрывается квадратной сеткой. При этом линейный размер сетки выбирается как степень числа два, например, . Тогда  и в соответствии с формулой (1) фрактальная размерность будет положительной. При увеличении размеров сетки количество ячеек необходимое для покрытия объекта растет. При этом отношение логарифмов стремится к постоянной величине, так что в большинстве случаев предел (1) существует и называется фрактальной размерностью. Основное преимущество ВС-алгоритмов заключается в их достаточно простой реализации в виде компьютерной программы. В то же время ВС-алгоритм отличается существенным недостатком, связанным с нелинейностью графика зависимости  на больших расчетных сетках.

Третий метод [1], [2], [3] расчета фрактальной размерности объектов на изображении, основан на расчетах спектров мощности с помощью преобразований Фурье. Для черно-белых изображений формула для спектра мощности имеет следующий вид:

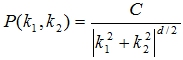                                                                          (2)

где d - показателем самоподобия, - волновые числа спектра мощности. Фрактальная размерность связана с показателем самоподобия следующим соотношением: . Диапазон значений фрактальной размерности изображения, как правило, равен: 2 < D < 3. Данное соотношение выражает тот факт, что изломанность яркостного поля изображения превышает размерность гладкой поверхности, однако при этом фрактальная размерность двухмерного изображения все же остается меньше размерности трехмерных объектов.

Мультифрактальный анализ позволяет более детально исследовать локальные фрактальные свойства объектов. Анализ основан на вычислении экспонент Холдера [14], [15]. Экспоненты Холдера вычисляются для каждого пикселя исходного изображения. В результате с помощью метода скользящего окна получается изображение экспоненты Холдера, которое называются α-изображением. При этом структура яркостного поля скользящего окна оценивается с помощью различных критериев, которые называются мерами, например, мера, которая оценивает степень подобия яркостей пикселей скользящего окна яркости центрального пикселя (iso - мера) или мера, которая вычисляет сумму яркостей пикселей в скользящем окне (s - мера).

Полученные α-изображения используются для расчета мультифрактальных спектров, для чего применяется следующая формула:

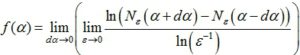                                          (3)

где α это параметр, который называется мерой мультифрактальности, а f(α) – называется мультифрактальным спектром,  – количество ячеек сетки, необходимое для покрытия мультифрактального множества при значениях параметра .

Для вычисления α-изображения каждый пиксель исходного изображения покрывается квадратным скользящим окном, в котором выполняется расчет величины параметра α. Вычисления выполняются по следующей формуле:

                                                                                  (4)

где μ – фрактальная мера, d – размер скользящего окна, C – коэффициент пропорциональности, α– локальная экспонента Холдера.

Если в качестве фрактальной меры использовать показатель подобия пикселей скользящего окна центральному пикселю (iso-мера), то расчетная формула принимает следующий вид

                                                (5)

где  – яркости центрального и текущего пикселей соответственно, 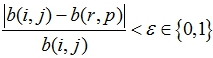, ε – заданный параметр подобия.

Если в качестве фрактальной меры использовать s-меру, то расчетная формула принимает следующий вид

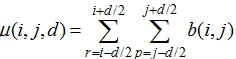                                                                 (6)

Для расчета фрактальной меры используется линейная регрессия формулы (4) в логарифмической шкале. Результатом вычисления является α-изображение с различными значениями величины α для каждого отдельного пикселя.

Далее осуществляется квантование α-изображения на заданное количество уровней. В результате получается совокупность бинарных изображений, для которых рассчитывается фрактальная размерность. График полученной фрактальной размерности  в зависимости от α называется мультифрактальным спектром. Далее вычисляется мультифрактальная скейлинговая экспонента τ(q), с помощью которой вычисляются обобщенные фрактальные размерности [1]:

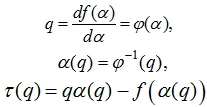                                                                               (7)

После вычисления скейлинговой экспоненты обобщенные фрактальные размерности, за исключением информационной размерности, вычисляются по следующей формуле [1]:

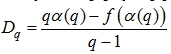                                                                          (8)

Информационная размерность графически или численно находится из решения уравнения [1]:

                                                                       (9)

Полученные результаты и их обсуждение. Изучение чувствительности мультифрактального анализа для фрактальной сегментации природных объектов проведено на примере изображения лесного покрова Центрального лесного государственного заповедника (ЦЛГЗ) (четвертый спектральный канал космического снимка со спутника Landsat7, размер снимка 647х647 пикселей). На снимке изображены два ландшафта: лесной и сельскохозяйственный. Для сравнения фрактальных характеристик на территории ландшафтов выбраны два фрагмента размером 200х200 пикселей. Эти фрагменты показаны в виде белых квадратов на космическом снимке (см. рис.1).

Для расчета α-изображений использованы две фрактальные меры: iso - мера и s-мера. При этом использованы следующие значения для максимальной ширины скользящего окна  и величины порога  (см. (5) и (6)). На рис.2 показаны исходные фрагменты изображения вместе со своими гистограммами яркости, а также α-изображения, рассчитанные с помощью iso- и s-мер. Изображения, представленные на рис.2, для улучшения визуализации растянуты на максимальный диапазон яркости (0 – 1), однако в расчетах используются реальные интервалы яркостей.

Рис.1. – Космический снимок ландшафтов ЦЛГЗ: квадратами обозначены фрагменты изображения, использованные для фрактального анализа

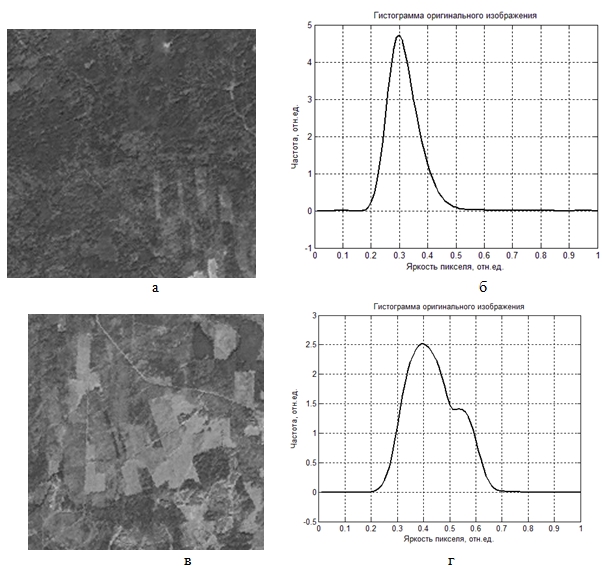
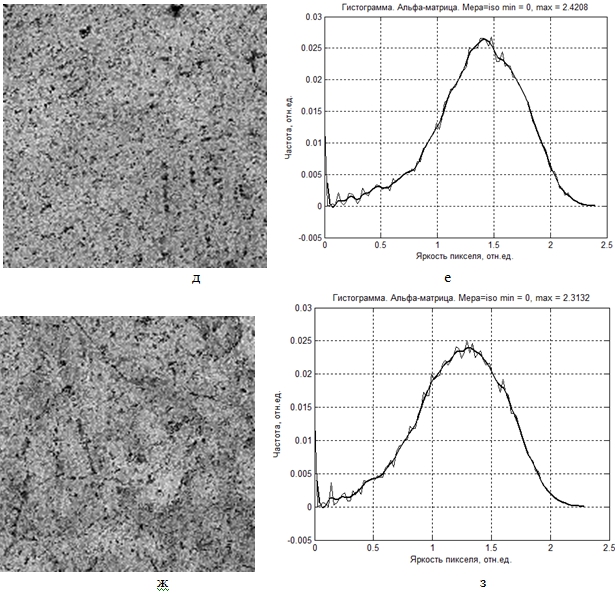
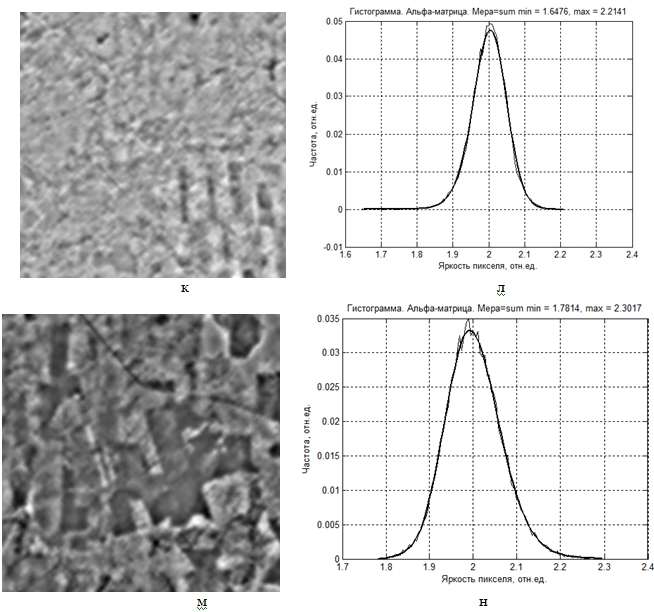
Рис.2 – Исходные фрагменты изображения (а, в) и их гистограммы (б, г), а также α-изображения iso-меры (д, ж) вместе с гистограммами (е, з) и s-меры (к, м) вместе с гистограммами (л, н)

С помощью α-изображений, показанных на рис.2, рассчитаны мультифрактальные спектры фрагментов космического снимка. Для расчетов определяются минимальное  и  максимальноезначение экспоненты Холдера на α-изображении. Далее вычисляется размер шага квантования: , где N – количество шагов квантования. В расчетах использовано N = 100. Мультифрактальные спектры, характеризующие фрактальные характеристики лесных и сельскохозяйственных ландшафтов, показаны на рис.3.

 

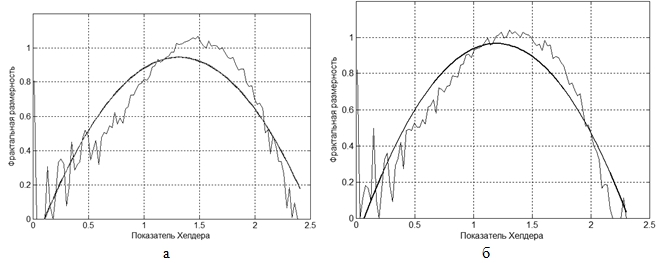
Рис.3 – Мультифрактальные спектры фрагментов космического снимка: а – лесной ландшафт, б – сельскохозяйственный ландшафт (полужирными линиями показаны квадратичные аппроксимации спектров)

Мультифрактальные спектры, показанные на рис.3, использованы для расчета скейлинговых экспонент τ(q) и обобщенных фрактальных размерностей. Результаты расчета графиков скейлинговых экспонент для мультифрактальных спектров, полученных с помощью iso-меры, показаны на рис.4. Обобщенные фрактальные размерности фрагментов представлены в табл. 1, а на рис.5, где показаны графики обобщенных фрактальных размерностей: D0 – нулевая обобщенная фрактальная размерность, D1 – информационная размерность, D2 – корреляционная размерность.

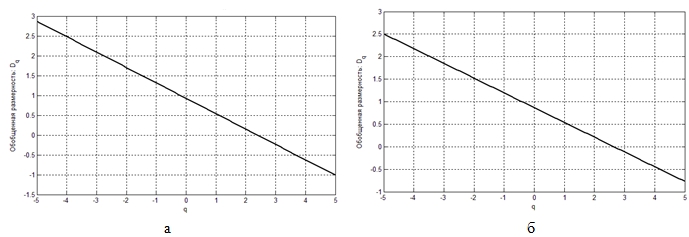
Рис.4 – Графики линейной аппроксимации скейлинговых экспонент: а – лесной ландшафт, б – сельскохозяйственный ландшафт

Как следует из рис.4, табл. 1 и рис.5, мультифрактальные характеристики ландшафтов различаются незначительно. Рассмотрим результаты численных оценок относительных величин, характеризующих различие обобщенных фрактальных размерностей, полученных для различных ландшафтов. Как следует из таблицы 1, обобщенные фрактальные размерности различаются в следующих пределах. Нулевая обобщенная размерность – D0 различается для разных ландшафтов в пределах 7.5 %. Информационная размерность – D1 различается для разных ландшафтов в пределах 0.4 %. Корреляционная размерность – D2 различается для разных ландшафтов в пределах 40 %. Таким образом, наибольшее различие обобщенных фрактальных размерностей получено для корреляционной размерности. Этот результат показывает, что наибольшей чувствительностью к особенностям ландшафта имеет корреляционная размерность, которая может быть предложена в качестве показателя, наилучшим образом характеризующего различия геометрической структуры ландшафтов.

Показанные на рис.2 α-изображения могут быть использованы для сегментации космических снимков. В работе [16] проведено исследование α-изображений и показано, что квантование α-изображений являются эффективным инструментом для выделения границ между нечеткими объектами.

Таблица 1 – Обобщенные фрактальные размерности фрагментов космического снимка

Обобщенные фрактальные размерности	Все изображение	Фрагмент 1	Фрагмент 2
D0	0.86272	0.9276	0.86752
D1	0.54199	0.53954	0.53982
D2	0.22125	0.15149	0.21212

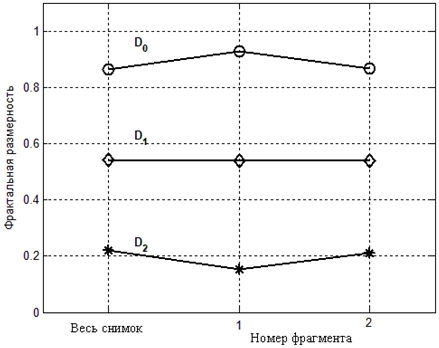
Рис.5 – Графики обобщенных фрактальных размерностей в зависимости от выбранного ландшафта: 1 – лесной ландшафт, 2 – сельскохозяйственный ландшафт

В данной работе, так же, как и в работе [16], проведено квантование α-изображения сельскохозяйственного ландшафта на десять уровней. На рис.6 показан результат квантования в виде бинарного изображения с достаточно четким выделением границ между объектами.

Рис.6 – Выделение границ между объектами изображения, полученный с помощью квантования α-изображения

Четкая структура границ на квантованном α-изображении (см. рис.6) подтверждает результаты, полученные авторами работы [16], и свидетельствует об эффективности использования для сегментации нечетких объектов на изображении и выделения границ между ними простой операции квантования.

Выводы. На основании проведенных исследований сделаны следующие выводы:

1. В результате проведенного мультифрактального анализа космического снимка земной поверхности в районе Центрального лесного заповедника установлено, что из трех обобщенных фрактальных размерностей наибольшее различие фрактальных характеристик для лесного и сельскохозяйственного ландшафтов имеет корреляционная размерность. Это позволяет сделать вывод о том, что корреляционная размерность может служить эффективным критерием сегментации и, таким образом, может быть использована в алгоритме сегментации лесных и сельскохозяйственных ландшафтов на космических снимках.
2. В результате квантования α-изображений установлено, что экспонента Холдера является эффективным показателем для выделения границ между нечеткими объектами на космическом изображении, что корреспондируется с результатами исследования авторов работы [16].

Список литературы / References

1. Божокин С.В. Фракталы и мультифракталы / С.В.Божокин, Д.А.Паршин – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 128с.
2. Кроновер Р.М. Фракталы и хаос в динамических системах / Р.М.Кроновер – М.: Постмаркет, 2000. – 352с.
3. Павлов А.Н. Мультифрактальный анализ сложных сигналов / А.Н.Павлов, B.C.Анищенко // Успехи физических наук. – 2007. – Т.177. – №8. – С.859-876.
4. Саркисов П.Д. Компьютерный метод анализа текстуры нанокомпозитов на основе расчета изолиний фрактальных размерностей / П.Д.Саркисов, О.Б.Бутусов, В.П.Мешалкин и др. // Теоретические основы химической технологии. – 2010. – Т.44 – №6. – С.620-625.
5. Макаренко Н.Г. Скейлинговые свойства цифровых изображений земных ландшафтов / Н.Г.Макаренко, Л.М.Каримова, О.А.Круглун // Современные проблемы дистанционного зондирования Земли из космоса. – 2014. – Т. 11. – № 2. – С. 26-37.
6. Макаренко Н.Г. Мультифрактальная сегментация данных дистанционного зондирования / Н.Г.Макаренко, О.А.Круглун, И.Н.Макаренко и др. // Исследование Земли из Космоса. – 2008. – № 3. – C.18-26.
7. Posadas A.N.D. Multifractal characterization of soil particle-size distributions / A.N.D.Posadas, D.Gimenez, M.Bittelli and others // Soil science society of America journal. – 2001. – V.65. – P. 1361–1367.
8. Folorunso O.A. Statistical and fractal evaluation of the spatial characteristics of soil surface strength / O.A.Folorunso, C.E.Puente, D.E.Rolston and others // Soil science society of America journal. – 1994. – V.58. – P.284–294.
9. Turiel A. The multifractal structure of satellite sea surface temperature maps can be used to obtain global maps of streamlines / A.Turiel, V.Nieves, E.Garcia-Ladona and others. // Ocean Science. – 2009. – № 5. – P.447–460.
10. Встовский Г.В. Введение в мультифрактальную параметризацию структур материалов / Г.В.Встовский, А.Г.Колмаков, И.Ж.Бунин – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 116с.
11. Reljin I.S. Fractal geometry and multifractals in analyzing and processing medical data and images / I.S.Reljin, B.D.Reljin // Archive of Oncology. – 2002. – V.10. – № 4. – P.283-293.
12. Lopes R. Fractal and multifractal analysis: a review / R.Lopes, N.Betrouni // Medical image Analysis. – 2009. – V.13. – № 4. – P.634-649.
13. Uahabi K.L. Applications of fractals in medicine / K.L.Uahabi, M.Atounti // Annals of the University of Craiova, Mathematics and Computer Science Series. – 2015. – V.42. – № 1. – P. 167–174.
14. Kolwankar Kiran M. Holder exponents of irregular signals and local fractional derivatives / Kiran M.Kolwankar, Anil D.Gangal // Journal of Physics. – 1997. – V. 48. – P.49-68.
15. Chakraborty Debasish. Segmentation and classification of high spatial resolution images based on Holder exponents and variance / Debasish Chakraborty, Sourabh Singh, Dibyendu Dutta // Geo-spatial Information Science. – 2017. – V.20. – № 1. – P.39-45.
16. Qi D. Multifractal spectrum theory used to medical image from CT testing / D.Qi, L.Yu // IEEE/ASME International Conference on Advanced Intelligent Mechatronics (02 Jul - 05 Jul 2008). –Xian, China: AIM, 2008. – P.68-73.

Список литературы на английском языке / References in English

1. Bozhokin S.V. Fraktaly i mul'tifraktaly [Fractals and multifractals] / S.V.Bozhokin, D.A.Parshin – Izhevsk: NIC «Reguljarnaja i haoticheskaja dinamika [Regular and chaotic dynamics]», 2001. – 128 P. [in Russian]
2. Kronover R.M. Fraktaly i haos v dinamicheskih sistemah [Fractals and chaos in dynamic systems] / R.M.Kronover – M.: Postmarket, 2000. – 352 P. [in Russian]
3. Pavlov A.N. Mul'tifraktal'nyj analiz slozhnyh signalov [Multifractal analysis of complex signals] / A.N.Pavlov, B.C.Anishhenko // Uspehi fizicheskih nauk [Advances in physical sciences]. – 2007. – T.177. – №8. – P.859-876. [in Russian]
4. Sarkisov P.D. Komp'juternyj metod analiza tekstury nanokompozitov na osnove rascheta izolinij fraktal'nyh razmernostej [Computer method for analyzing the texture of nanocomposites based on the calculation of level lines of fractal dimensions] / P.D.Sarkisov, O.B.Butusov, V.P.Meshalkin and others // Teoreticheskie osnovy himicheskoj tehnologii [Theoretical foundations of chemical technology] – 2010 – V.44 – №6. – P.620–625. [in Russian]
5. Makarenko N.G. Skejlingovye svojstva cifrovyh izobrazhenij zemnyh landshaftov [Scaling properties of digital images of terrestrial landscapes] / N.G.Makarenko, L.M.Karimova, O.A.Kruglun // Sovremennye problemy distancionnogo zondirovanija Zemli iz kosmosa [Modern problems of Earth remote sensing from space]. – 2014. – V. 11. – № 2. – P. 26–37. [in Russian]
6. Makarenko N.G. Mul'tifraktal'naja segmentacija dannyh distancionnogo zondirovanija [Multifractal segmentation of remote sensing data] / N.G.Makarenko, O.A.Kruglun, I.N.Makarenko and others // Issledovanie Zemli iz Kosmosa [Exploring the Earth from Space]. – 2008. – № 3. – P.18–26. [in Russian]
7. Posadas A.N.D. Multifractal characterization of soil particle-size distributions / A.N.D.Posadas, D.Gimenez, M.Bittelli and others // Soil science society of America journal. – 2001. – V.65. – P. 1361–1367.
8. Folorunso O.A. Statistical and fractal evaluation of the spatial characteristics of soil surface strength / O.A.Folorunso, C.E.Puente, D.E.Rolston and others // Soil science society of America journal. – 1994. – V.58. – P.284–294.
9. Turiel A. The multifractal structure of satellite sea surface temperature maps can be used to obtain global maps of streamlines / A.Turiel, V.Nieves, E.Garcia-Ladona and others // Ocean Science. – 2009. – № 5. – P.447–460.
10. Vstovskij G.V. Vvedenie v mul'tifraktal'nuju parametrizaciju struktur materialov [Introduction to multifractal parametrization of material structures] / G.V.Vstovskij, A.G.Kolmakov, I.Zh.Bunin – Izhevsk: NIC «Reguljarnaja i haoticheskaja dinamika [Regular and chaotic dynamics]», 2001. – 116 P. [in Russian]
11. Reljin I.S. Fractal geometry and multifractals in analyzing and processing medical data and images / I.S.Reljin, B.D.Reljin // Archive of Oncology. – 2002. – V.10. – № 4. – P.283-293.
12. Lopes R. Fractal and multifractal analysis: a review / R.Lopes, N.Betrouni // Medical image Analysis. – 2009. – V.13. – № 4. – P.634-649.
13. Uahabi K.L. Applications of fractals in medicine / K.L.Uahabi, M.Atounti // Annals of the University of Craiova, Mathematics and Computer Science Series. – 2015. – V.42. – № 1. – P. 167–174.
14. Kolwankar Kiran M. Holder exponents of irregular signals and local fractional derivatives / Kiran M.Kolwankar, Anil D.Gangal // Journal of Physics. – 1997. – V. 48. – P.49-68.
15. Chakraborty Debasish. Segmentation and classification of high spatial resolution images based on Holder exponents and variance / Debasish Chakraborty, Sourabh Singh, Dibyendu Dutta // Geo-spatial Information Science. – 2017. – V.20. – № 1. – P.39-45.
16. Qi D. Multifractal spectrum theory used to medical image from CT testing / D.Qi, L.Yu // IEEE/ASME International Conference on Advanced Intelligent Mechatronics (02 Jul - 05 Jul 2008). –Xian, China: AIM, 2008. – P.68-73.