К ВОПРОСУ ВЛАГОПРОНИЦАЕМОСТИ МНОГОФАЗНОЙ ГРУНТОВОЙ СРЕДЫ ПРИ НЕПОЛНОМ ВОДОНАСЫЩЕНИИ

Тедеев Т.Р.

ORCID: 0000-0002-2994-1942, кандидат технических наук,

Южный математический институт Владикавказского научного центра Российской академии наук в г. Владикавказе, РСО-Алания

К ВОПРОСУ ВЛАГОПРОНИЦАЕМОСТИ МНОГОФАЗНОЙ ГРУНТОВОЙ СРЕДЫ ПРИ НЕПОЛНОМ ВОДОНАСЫЩЕНИИ

Аннотация

Представлено решение нелинейного уравнения влагопроницаемости в многофазной грунтовой среде  с учетом полученной зависимости для скорости распространения фронта смачивания. Скорость перемещения  фронта смачивания в многофазной грунтовой среде не постоянна: она максимальна в начальный момент времени, а затем существенно снижается. Сделана попытка построения общих основ влагопроницаемости в многофазной грунтовой среде путем разделения потенциала грунтовой влаги на составляющие слагаемые. Показано, что инфильтрационные зоны влагопереноса имеют формальный характер и не обоснованы ни теорией, ни экспериментом.

Ключевые слова: влагопроницаемость, многофазная грунтовая среда, потенциал грунтовой влаги, фронт смачивания, структурные разновидности влаги.

Tedeev T.R.

ORCID: 0000-0002-2994-1942, PhD in Engineering,

Southern Mathematical Institute of Vladikavkaz Scientific Center of RAS Russian Academy of Sciences in Vladikavkaz, North Ossetia-Alania

ON ISSUE OF WATERPROOF OF A MULTI-PHASE SOIL GROUND UNDER INCOMPLETE WATER SATURATION

Abstract

The solution of the nonlinear equation of moisture permeability in soil medium is presented, considering the dependence obtained for the propagation velocity of the moisting front. The traversing speed of the moisting front in a multiphase soil medium is not constant: it is maximum at the initial moment of time, and then decreases significantly. The authors attempted to construct general principles of moisture permeability in a multiphase soil medium by dividing the ground moisture potential into constituent terms. It is shown that the infiltration zones of moisture transfer are of a formal nature and are not substantiated by either theory or experiment.

Keywords: moisture permeability, multiphase soil environment, soil moisture potential, moisting front, structural varieties of moisture.

В связи с освоением районов распространения структурно-неустойчивых грунтов и строительством сооружений различного назначения на них, проблема  количественного прогнозирования влагопроницаемости многофазной грунтовой среды приобретает все большую актуальность.

Основной целью работы является создание общих основ влагопроницаемости в многофазной грунтовой среде путем разделения потенциала грунтовой влаги на составляющие слагаемые и самостоятельное исследование каждого отдельного слагаемого - как задачи для достижения поставленной цели.

Известно [1, С. 24], [2, С. 6], [3, С. 27], [4, С. 15], что влага в грунтовой среде может находиться под влиянием сил, имеющих различную природу: адсорбционных (монослойной и полислойной), осмотических, капиллярных и гравитационных. Величина этих сил зависит от минералогического и гранулометрического составов, исходной влажности, плотности скелета среды, концентрации порового раствора и нагрузки, действующей на многофазную среду [5, С. 246], [6, C. 38], [8, С. 10], [9, С. 5], [10, С. 143]. Полный потенциал, зависящий от совокупности действия силовых полей, в этом случае подразделяется на отдельные слагаемые, соответствующие каждому силовому полю.

Следуя [4, С. 84], ненасыщенный поток грунтовой влаги имеет две, существенно, отличительные особенности. Во-первых, влага вледствие электромолекулярного притяжения молекул воды к поверхности частиц  движется от участков с толстыми водными пленками к участкам с тонкими пленками, поэтому движущая сила электромолекулярного переноса достигает максимального значения вблизи фронта смачивания. Гравитационная сила в этом потоке ничтожна мала по сравнению с адсорбционными и осмотическими, но с течением времени по мере увеличения толщины водной пленки возрастает.

Во-вторых, площадь поперечного сечения ненасыщенного потока зависит от степени его водонасыщенности. При низкой влажности фактор проницаемости значительно снижается, с увеличением же влажности - увеличивается. Поэтому, чем толще пленка влаги на поверхности частиц грунтовой среды, тем большее количество влаги способно передвигаться через эту же среду.

Согласно исследованиям [4, С. 86], [6, C. 66], скорость влагопроницания в единицу времени через единичную площадь многофазной грунтовой среды можно определить следующим образом:

                                                                           (1)

где - коэффициент водопроницаемости несплошного потока;

        Ф    - суммарный потенциал грунтовой влаги в рассматриваемой задаче:

                                                         (2)

здесь  - потенциал полислойной влаги:

                                                                               (3)

 - потенциал диффузионной влаги:

                                                                               (4)

 - потенциал капиллярной влаги:

                                                                                (5)

где  - давления и плотности соответственно полислойной, диффузионной и капиллярной влаги.

В первом приближении зависимость между давлением поровой влаги P_w и влажностью грунтовой среды W  в дифференциальной форме можно представить в виде линейной функции:

                                                                                    (6)

где   - коэффициент пропорциональности.

Заметим, что зависимость (6) интегрируется с учетом предельных значении интервала изменения каждой структурной разновидности влаги.

После выполнения интегрирования, окончательно можно получить зависимости между давлением и влажностью [6, С. 66]:

- для полислойной влаги

                                                                         (7)

- для диффузионной влаги

                                                                             (8)

- для капиллярной влаги

                                                                            (9)

Пользуясь полученными соотношениями (2)-(5) и (7)-(9) для скорости влагопереноса в многофазной грунтовой среде можно получить:

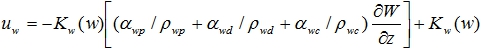  (10)

Закон сохранения массы для движущейся в многофазной грунтовой среде произвольным образом жидкости выражается уравнением неразрывности или сплошности [4, С. 85].  В задачах влагопроницаемости без учета внутренних распределенных источников влаги, условие неразрывности влажностного потока будет иметь следующий вид [6, С. 6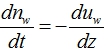1]:

                                                                                     (11)

где         - скорость влагопроницания через единичную площадь многофазной грунтовой среды;

                t - время;

При этом известно [4, С. 85], что задача влагопереноса в многофазной грунтовой среде под действием сил всасывания сводится к рассмотрению несплошного потока через поровое пространство многофазной среды.

Для определения площади несплошного потока влаги в этом случае можно воспользоваться величиной  коэффициента водонасыщенности многофазной грунтовой среды:

                                                                                           (12)

где n – пористость грунтовой среды.

Зависимость для определения коэффициента водонасыщенности имеет вид

                                                                                     (13)

где  - влажность, которая соответствует полному заполнению среды

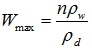                                                                                           (14)

где W- естественная влажность среды; - плотность скелета многофазной

грунтовой среды;  - плотность поровой жидкости.

          Окончательно, для многофазной грунтовой среды скорость изменения площади несплошного потока влаги в порах среды во времени определится как

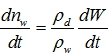                                                                                        (15)

Подставляя полученные выражения для скорости влагопроницания и изменения площади потока влаги во времени из (10) и (15) в уравнение неразрывности (11), получим

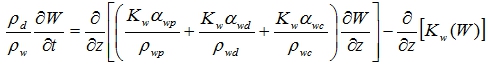                                                          (16)

при соответствующем начальном условии

                                                                                          (17)

а на границе – граничного условия

                                                                                            (18)

Принимая известные зависимости [4, С. 86], [6, C. 74] для коэффициентов проницаемости K(W) и диффузии D(W) многофазной грунтовой среды, нелинейное дифференциальное уравнение (16) принимает вид:

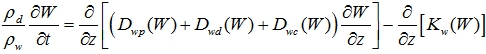  (19)

где K_w(W) – коэффициент влагопроницаемости грунтовой среды по

                    С.Ф. Аверьянову [4, С. 86], [6, C. 74]:

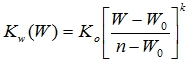                                                                     (20)

 - коэффициент диффузии пленочной влаги

                                              (21)

Здесь: W₀ - влага, прочносвязанная поверхностью грунтовой среды;

            K₀ - коэффициент влагопроницаемости при полном влагонасыщении  грунтовой среды;

                  - коэффициент диффузии для каждой структурной разновидности влаги [6, С. 74].

Следуя [7, С. 30], для построения автомодельного решения следует ввести в уравнение (19) волновую переменную

                                                                                                 (22)

Для разности естественной и прочносвязанной влажностей можно принять обозначение  , относительно которой получим  обыкновенное дифференциальное уравнение

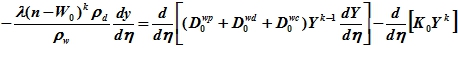             (23)

которое равнозначно:

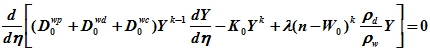           (24)

Согласно [7, С. 30], для получения решения дифференциального уравнения (24),  необходимо принять

                           (25)

Приняв сокращенное обозначение для суммы коэффициентов диффузии многофазной грунтовой среды

                                                                             (26)

нелинейное дифференциальное уравнение принимает вид:

                                          (27)

Решением дифференциального уравнения (25) является следующая функция

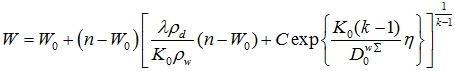            (28)

Постоянные интегрирования  и С определяются из начального и граничного условии (17)-(18).

При этом известно, что на фронте смачивания, координаты которого определяются как , влажность грунтовой среды равна начальной, то есть  W=W₀ . Это условие позволяет найти постоянную С:

                                                                              (29)

Для определения постоянной  можно воспользоваться условием  (18), которое приводит к следующей зависимости

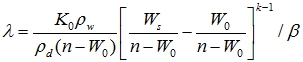                   (30)

где

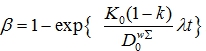                                          (31)

В первом приближении физически оправданное решение для скорости перемещения фронта смачивания с учетом текущего времени и функциональных зависимостей коэффициента диффузии для каждой структурной разновидности влаги можно получить из разложения зависимости (31) в ряд и удержанием первых двух членов ряда. В этом случае для определения скорости распространения фронта смачивания получим:

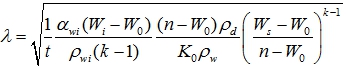                (32)

Подставляя соотношения (29) и (32) в уравнение (28) получим зависимость для определения влажности грунтовой среды в зависимости от предела  проницания влаги и текущего времени:

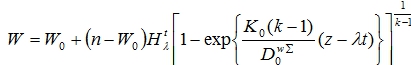             (33)

где

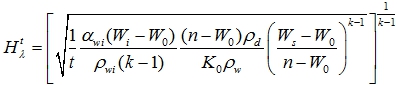                           (34)

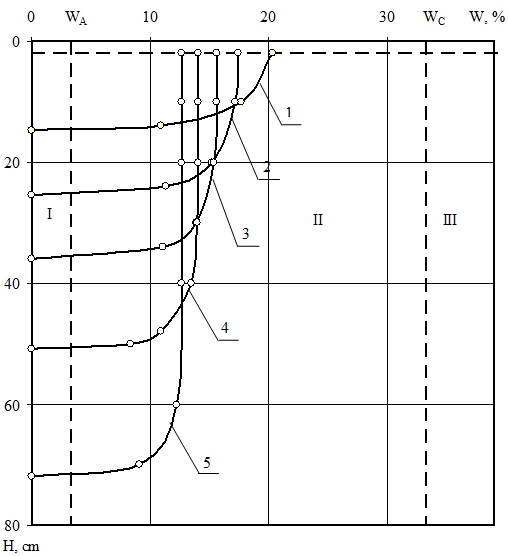
Приведенные теоретические основы влагопроницаемости и разработанная методика позволили решить модельную задачу по определению профиля влажности в разные моменты времени (t=1 сутки, 3 сут., 6 сут., 12 сут., 24 сут.) При этом многофазная грунтовая среда увлажняется из полосы –W_s=0.3, начальная влажность среды W(z,0)=W₀=0.03. В расчетах были приняты следующие численные  значения параметров:  см/с, n=0.4, m=0.6, =1.62 г/см³, =1 г/см³, к=3.56, =0.006 МПа. Результаты расчета влагопереноса грунтовой влаги по глубине и во времени представлены на рис. 1.

Сравнительный анализ полученных кривых изменения влажности по глубине и во времени показал, что характерные зоны влагопереноса, наблюдаемые экспериментально, не всегда имеют место в полном объеме. По всей видимости инфильтрационные зоны влагопереноса имеют формальный характер и не обоснованы ни теорией, ни экспериментом. К примеру, кривые 1 и 2 на рис. 1  имеют четко выраженную переходную зону, как продолжение зоны насыщения. Переходная зона плавно переходит в зону смачивания, отсутствует передаточная зона. Кривые же 3,4 и 5 на рис.1, наоборот, не имеют переходную зону. Передаточная зона берет начало от зоны насыщения и плавно переходит в зону смачивания.

Обобщая полученные результаты в первом приближении можно сделать следующие выводы:

• Полученное аналитическое решение нелинейного уравнения влагопроницаемости в многофазной грунтовой среде позволяет дать оценку как скорости распространения фронта смачивания, так и скорости влагопроницаемости в целом.
• Скорость распространения фронта смачивания не постоянна: она максимальна в начальный момент времени, а затем существенно снижается.
• Сделана попытка построения общих основ влагопроницаемости в многофазной грунтовой среде путем разделения потенциала грунтовой влаги на составляющие слагаемые и самостоятельного исследования каждого отдельного слагаемого.
• Показано, что учет нелинейности коэффициента влагопроницаемости существенно влияет на общий вид профиля влажности в грунтовой среде, скорость влагопроницания и скорость перемещения фронта смачивания.
• Важным преимуществом аналитического решения нелинейного уравнения влагопроницаемости является возможность определения закономерностей проницания структурных разновидностей влаги при инфильтрации на всем интервале неполного водонасыщения.

Рис.1 – Кривые изменения влажности в зависимости от времени (1–1 сут., 2–3 сут., 3–6 сут., 4–12 сут., 5–24 сут.).

I-область прочносвязанной влаги W ≤ W_A II-область диффузионной влаги W_A < W ≤ W_C III-область насыщения порового пространства W_C < W ≤ W_S

 

Список литературы/References

1. Полубаринова-Кочина П.Я. Теория движения грунтовых вод / П.Я. Полубаринова-Кочина. -М.: Наука, 1977. -664c.
2. Филип Дж. Изотермическое движение влаги в зоне аэрации / Дж. Филип. -Л.: Гидрометеоиздат, 1972. -168с.
3. Бэр, Я.Д. Физико-математические вопросы фильтрации воды / Я.Д. Бэр, С. Заславский, С. Ирмей. -М.: Мир, 1971. -452c.
4. Тер-Мартиросян З.Г. Прогноз механических процессов в массивах многофазных грунтов / З.Г. Тер-Мартиросян. -М.: Недра, 1986. -292с.
5. Цытович, Н.А. Основы прикладной геомеханики в строительстве / Н.А. Цытович, З.Г. Тер-Мартиросян. -М.: Высшая школа, 1981. -318c.
6. Тедеев, Т.Р. Методология и алгоритмы расчета полей влажности в задачах проектирования грунтовых сооружений / Т.Р. Тедеев, Г.Г. Арунянц. –Владикавказ: Терек, 2005. -203 с.
7. Самарский, А.А. Режимы с обострением в задачах для квазилинейных параболических уравнений / А.А. Самарский, В.А. Галактионов, С.П. Курдюмов, А.Г. Михайлов. -М.: Наука, 1987. -476 c.
8. Karl Terzaghi, Ralfh B. Peck, Golamreza Mesri. Soil Mechanics in Engineering Practice / Karl Terzaghi, Ralfh B. Peck, Golamreza Mesri // Third Edition, 1995, 549 p.
9. Steven L. Kramer. Geotechnical Earthquake Engineering / Steven L. Kramer // University of Washington, 1996, 653 p.
10. James K. Mitchell. Fundamentals of soil behavior / James K. Mitchell // second Edition, 1993, 437 p.

Список литературы на английском языке / References in English

1. Polubarinova-Cochina P.Ya. Teoriya dvizheniya gruntovykh vod [Theory of Groundwater Motion] / P.Ya. Polubarinova-Kochina. -M .: Science, 1977. - 664p. [in Russian]
2. Philip J. Izotermicheskoye dvizheniye vlagi v zone aeratsii [Isothermal Motion of Moisture in Aeration Zone] / J. Philip. - L.: Gidrometeoizdat, 1972.-168p. [in Russian]
3. Baer J.D. Fiziko-matematicheskiye voprosy filtratsii vody [Physical and Mathematical Problems of Water Filtration] / J.D. Baer, S. Zaslavsky, S. Irmei. - M.: World, 1971. - 452p.
4. Ter-Martirosyan Z.G. Prognoz mekhanicheskikh protsessov v massivakh mnogofaznikh gruntov [Forecast of mechanical processes in arrays of multiphase soils] / Z.G. Ter-Martirosyan. - M.: Nedra, 1986. -292p. [in Russian]
5. Tsytovich, N.A. Osnovy prikladnoy geomekhaniki v stroitelstve [Fundamentals of Applied Geomechanics in Construction] / N.А. Tsytovich, Z.G. Ter-Martirosyan. - M.: High School, 1981. - 318p. [in Russian]
6. Tedeev T.R. Metodologiya i algoritmy rascheta poley vlazhnosti v zadachakh proektirovaniya gruntovykh sooruzheniy [Methodology and Algorithms for Calculating Moisture Fields in Problems of Design of Soil Structures] / Т.R. Tedeev, G.G. Arunyants. - Vladikavkaz: Terek, 2005. -203 p. [in Russian]
7. Samarsky, A.A. Regimy s obostreniem v zadachakh dlia kvazilineynykh parabolicheskikh uravneniy [Regimes with Peaking in Problems for Quasilinear Parabolic Equations] // A.A. Samarskiy, V.A. Galaktionov, S.P. Kurdyumov, A.G. Mikhailov. - M.: Science, 1987. - 476 p. [in Russian]
8. Karl Terzaghi, Ralfh B. Peck, Golamreza Mesri. Soil Mechanics in Engineering Practice / Karl Terzaghi, Ralfh B. Peck, Golamreza Mesri // Third Edition, 1995, 549 p.
9. Steven L. Kramer. Geotechnical Earthquake Engineering / Steven L. Kramer // University of Washington, 1996, 653 p.
10. James K. Mitchell. Fundamentals of soil behavior / James K. Mitchell // second Edition, 1993, 437 p.