К ВОПРОСУ АППРОКСИМАЦИИ ЭМПИРИЧЕСКИХ ЗАВИСИМОСТЕЙ

Середа С.Н.

ORCID: 0000-0002-9982-5875, кандидат технических наук, Доцент,

Муромский институт (филиал) Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых

К ВОПРОСУ АППРОКСИМАЦИИ ЭМПИРИЧЕСКИХ ЗАВИСИМОСТЕЙ

Аннотация

В статье представлены результаты математического моделирования эмпирических зависимостей на примере аппроксимации частотной характеристики акустической камеры. Предложена оригинальная модель функции аппроксимации амплитудно-модулированного затухающего сигнала. Приводятся количественные оценки параметров модели с использованием линеаризации нелинейных функций. Результаты исследования могут быть использованы для разработки шумозащитных экранов и решении прикладных задач математической статистики.

Ключевые слова: функция аппроксимации, линеаризация, математическая модель, частотная характеристика, шумозащита.

Sereda S.N.

ORCID: 0000-0002-9982-5875, PhD in Engineering, Associate Professor,

Murom Institute (Branch) of the Vladimir State University named after Alexander Grigorievich and Nikolai Grigorievich Stoletov

TO THE QUESTION OF EMPIRICAL DEPENDENCIES APPROXIMATION

Abstract

The article presents the results of mathematical modeling of empirical dependencies on the example of the approximation of acoustic chamber frequency characteristic. An original model of the approximation function of an amplitude-modulated damped signal is proposed. Quantitative estimates of the model parameters using the linearization of nonlinear functions are given. The results of the research can be used to develop noise shielding screens and solve applied problems of mathematical statistics.

Keywords: approximation function, linearization, mathematical model, frequency response, noise protection.

Во многих областях науки и техники возникает задача обработки результатов эксперимента и идентификации зависимостей между параметрами процесса или системы, которая может сводиться к поиску некоторой аналитической функции аппроксимации табличных эмпирических данных, что позволяет в дальнейшем проводить расчеты путем интерполяции и экстраполяции функции и прогнозировать динамику процесса. Хотя разработаны различные методы решения задачи аппроксимации, как-то кусочно-линейная аппроксимация, аппроксимация тригонометрическими функциями, полиномами Чебышева и др., в некоторых случаях не удается с помощью таких подходов получить приемлемо хорошее приближение, либо аналитическая функция не позволяет получить общую математическую модель исследуемого процесса как, например, при использовании сплайнов. При этом выдвижение гипотезы о виде функции аппроксимации должно учитывать дополнительную информацию о характере процесса, что скорее является искусством. Кроме того, определение значений параметров функции аппроксимации, обеспечивающих наилучшее приближение в смысле минимизации критерия среднеквадратического отклонения, может проводиться как аналитически, так и алгоритмически [1, C. 292], [2, C. 145], [8], [10].

Рассмотрим задачу поиска функции аппроксимации частотной характеристики акустической камеры, используемой в качестве лабораторного макета для оценки эффективности звукопоглощающих экранов [5, C. 18].

Цель исследования заключалась в определении собственной амплитудно-частотной характеристики (АЧХ) акустического экрана на основе резонатора Гельмгольца, установленного в лабораторную акустическую камеру [6]. Измерения уровня шума в камере проводились с помощью шумомера ВШВ-003. В качестве источника звука использовался генератор звуковой частоты TR-0157/002, усилитель звуковой частоты и акустическая система из двух колонок "ОДА". Измерения проводились в треть октавных полосах частот, в диапазоне от 25 Гц до 8000 Гц. В данном диапазоне частот преобладает энергия большинства производственных, бытовых и транспортных шумов [7, C. 19].

Методика измерений амплитудно-частотной характеристики исследуемой системы включала следующие этапы [4, C. 28]:

Сначала замерялась интенсивность отраженного от глухой стенки звука (без резонатора). Производили три замера уровня звукового давления на каждой частоте перед глухой стенкой, затем находили среднее значение L_г.

Далее в камеру помещался экран, направленный щелями к источнику звука, и проводились измерения звукового давления перед экраном при разных настройках геометрических параметров резонатора L_р. Для каждого состояния было произведено несколько замеров и определялось средний статистический уровень звукового давления, чтобы минимизировать ошибки измерений.

Эмпирическая АЧХ звукопоглощающего экрана определялась как разность результатов измерений двух предыдущих этапов

L_э=L_г – L_р    (1)

Частотная характеристика звукопоглощающего экрана L_э(x) (рис.1) получена при следующих значениях геометрических параметров резонатора: глубина короба h=75 мм, ширина щели b=0,5 мм, расстояние между щелями l=90,75 мм, глубина щели i=15 мм.

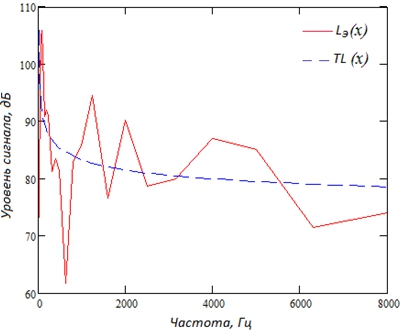
Рис. 1 – Эмпирическая частотная характеристика звукопоглощающего экрана

 

Для поиска аналитической функции, аппроксимирующей данные эксперимента, сделаем допущение о характере изменения анализируемой кривой. Во-первых, функция не является гладкой и содержит как максимумы, так и провалы на частотах, кратных резонансной частоте экрана. Во-вторых, как видно из рисунка, линия тренда TL(x), вычисленная путем усреднения, представляет собой монотонно убывающую кривую с ростом частоты. Проведем предварительную обработку путем нормирования эмпирической характеристики на ее максимум, и в дальнейшем будем проводить аппроксимацию нормированной характеристики L(x). Поскольку в эксперименте измерения проводились на наборе одно-тональных гармонических сигналов звукового диапазона частот, то можно принять гипотезу о частотном отклике звукопоглощающего экрана в форме амплитудно-модулированного затухающего сигнала соответствующей частоты [9]. Это позволяет определить математическую модель анализируемой характеристики в виде

S(x)=S₁(x)+S₂(x)*S₃(x)   (2)

где S₁(x) – функция тренда; S₂(x) – функция амплитуды; S₃(x) – несущая функция; x – частотная координата.

Относительно вида функций, являющихся составными частями модели могут быть различные предположения. Предварительный анализ данных эксперимента, а также линии тренда позволяет поставить задачу оценки параметров функции аппроксимации вида

S(x)=exp (a₁∙x^b1)+a₂∙exp (b₂∙x) ∙ sin (ω∙x+φ)   (3)

где a₁, a₂, b₁, b₂ – параметры функции; ω – частота резонатора; φ – фазовый сдвиг.

Для определения значений параметров искомой функции воспользуемся методом приведения зависимостей к линейному виду для её составляющих. Так можно получить формулы линеаризации для функции тренда S₁(x) (4) и функции амплитуды (5) соответственно.

Y₁= ln(S₁(x))= a₁∙x^b1; U₁=A+b₁∙Z₁;  A=lg(a₁); Z₁=lg(x); U₁=lg(–Y₁)     (4)

Y₂= S₂(x)= a₂∙exp (b₂∙x); U₂=ln(a₂)+b₂∙x;  U₂=ln(Y₂)    (5)

В качестве критерия приближения принимаем минимум среднеквадратического отклонения

   (6)

Достижению минимума целевой функции (6) в случае линейной зависимости с двумя параметрами a_i, b_i соответствует равенство нулю первых частных производных [1, C. 345], [3, C. 153]

   (7)

Раскрытие выражения (7) в отношении функций S₁(x) и S₂(x) приводит к системам нормальных уравнений (7) и (8) соответственно

   (8)

       (9)

Решение указанных систем уравнений в программе математического моделирования MathCad с помощью встроенной функции lsolve(a_i,b_i) дает значения параметров a₁=–0.015, b₁=0.505, a₂=0.288673, b₂=–0.004712.  При этом, значение ошибки составляет Q₁=2.7*10^-7 и Q₂=3.8*10^-7.

Оценка параметров функции S₃(x) проводилась алгоритмически методом итераций, где критерием остановки итерационного процесса было совпадение глобального максимума и минимума на частоте провала функции аппроксимации S(x) с данными эксперимента. В результате поиска были получены значения параметров ω=420, φ=6.41, что позволяет установить их прямую взаимосвязь с резонансной частотой акустического экрана f_p, определяемой по его геометрическим характеристикам [6]

     (10)

где f_m – частота глобального максимума эмпирической функции L(x); f_р – резонансная частота акустического экрана, определяемая по [6]

где  b - ширина щели; h - глубина короба; i - глубина щели; l - расстояние между щелями; с=331 м/с – скорость звука в воздухе при температуре воздуха 20°С.

Результаты математического моделирования функции аппроксимации с установленными значениями параметров показаны на рис. 2. В качестве меры адекватности модели примем коэффициент корреляции, показывающий степень совпадения кривых, который составил 97,4%. Как видно из рисунка предложенная аналитическая функция достаточно точно локализует частоты, в которых наблюдаются глобальный максимум и основной провал при приемлемом приближении в остальном диапазоне частот. Полученная модель позволяет в дальнейшем рассчитать частотную характеристику шумозащитного экрана при изменении его конструктивных параметров и оценивать степень звукопоглощения.

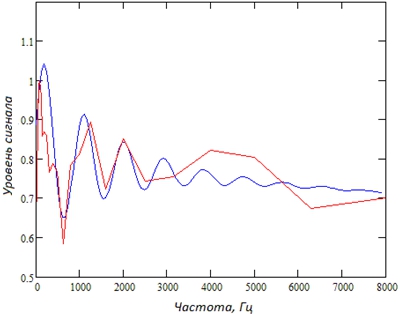
Рис. 2 – Аппроксимация нормированной частотной характеристики L(x) функцией S(x)

Список литературы / References

1. Амосов А.А. Вычислительные методы для инженеров: Учеб. пособие / А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова. – М. : Высш. шк., 1994. – 544 с.
2. Большаков А.А. Методы обработки многомерных данных и временных рядов: Учеб. пособие для вузов / А.А. Большаков, Р.Н. Каримов. – М. : Горячая линия – Телеком, 2007. – 522 с.
3. Гумеров А.М. Математическое моделирование химико-технологических процессов: Учеб. пособие / А.М. Гумеров. – 2-е изд. – СПб. : Издательство «Лань», 2014. – 176 с.
4. Гуськов П.М. Выбор уровня звукового давления в лабораторной акустической камере при исследовании характеристик шумозащитных экранов / П.М. Гуськов // Методы и устройства передачи и обработки информации. – 2017. – №1. – С. 28–31.
5. Калиниченко М.В. Некоторые аспекты применения резонансных поглотителей на урбанизированных территориях / М.В. Калиниченко // Машиностроение и безопасность жизнедеятельности. – 2013. – № 4. – С. 18–24.
6. Патент ПМ №139578 Российская Федерация, E01F8/00. Шумопоглотитель / Булкин В. В. Калиниченко М. В.; заявитель и патентообладатель Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых. – №2013121443; заявл. 07.05.2013; опубл. 20.04.2014.
7. Bulkin V. V. Preliminary results of development and test of the lab anechoic chamber / V. V. Bulkin, M. V. Kalinichenko // Noise Theory and Practice, vol. 2. – 2016. - №2. – P. 19–26.
8. Powell M. J. D. Approximation Theory and Methods / M.J.D. Powell. – Cambridge University Press, 1981. – 339 p.
9. Sereda S.N. Mathematical Model of Acoustic Baffle based on Helmholtz Resonator / S.N. Sereda, V.V Bulkin, M.V. Kalinichenko, P.M. Guskov P.M. // IEEE Conference 2017 Dynamics of Systems, Mechanisms and Machines (Omsk, 2017).
10. Steffens Karl-Georg. The History of Approximation Theory. From Euler to Bernstein / Karl-Georg Steffens. – Boston: Birkhauser, 2006. – 219 p.

Список литературы на английском языке / References in English

1. Amosov A. A. Vychislitelnye metody dlya ingenerov: ucheb. posobie [Computational methods for engineers: Textbook] / A. A. Amosov, Yu. A. Dubinsky, N. V. Kopchenova. – M.: Vysshaya shkola, 1994. – 544 p. [in Russian]
2. Bolshakov A. A. Metody obrabotky mnogomernych dannych i vremennych ryadov: ucheb. posobie [Methods for processing multidimensional data and time series: Textbook] / A. A. Bolshakov, R. N. Karimov. – M.: Hot line – Telekom, 2007. – 522 p. [in Russian]
3. Gumerov A. M. Matematicheskoe modeliravanie chimiko-technologicheskich processov: ucheb. posobie. [Mathematical modeling of chemical-technological processes: Textbook] / A. M. Gumerov. – 2nd edition. – SPb.: Lan publishing, 2014. – 176 p. [in Russian]
4. Guskov P. M. Vybor urovnya zvukovogo davlenia v laboratornoy akusticheskoy kamere pri issledovanii charakteristik shumozaschitnych ekranov [Choice of the sound pressure level in a laboratory acoustic chamber in the study of the characteristics of the noise protecting screens] / P. M. Guskov // Metody i ustroistva peredachy i obrabotky informatcii [Methods and devices of the information processing and transmission]. – 2017. – №1. – P. 28–31. [in Russian]
5. Kalinichenko M. V. Nekotorye aspekty primenenia resonansnych poglotiteley na urbaniziravannych territoriach [Some aspects of the resonance absorbers employment in urban areas] / M. V. Kalinichenko // Mashinostroenie i bezopasnost zhiznedeyatelnosty [Engineering industry and life safety]. – 2013. – № 4. – P. 18–24. [in Russian]
6. Pat. PM №139578 Russian Federation, E01F8/00. Shumopoglotitel [Acoustic absorber] / Bulkin V. V., Kalinichenko M. V.; the applicant and the patentee Vladimir State University n.a. A.G. and N.G. Stoletovs. – №2013121443; appl. 05/07/13; publ. 04.20.14. [in Russian]
7. Bulkin V.V. Preliminary results of development and test of the lab anechoic chamber / V.V. Bulkin, M. V. Kalinichenko // Noise Theory and Practice, vol. 2. – 2016. – №2. – P. 19–26.
8. Powell M. J. D. Approximation Theory and Methods / M.J.D. Powell. – Cambridge University Press, 1981. – 339 p.
9. Sereda S.N. Mathematical Model of Acoustic Baffle based on Helmholtz Resonator / S.N. Sereda, V.V Bulkin, M.V. Kalinichenko, P.M. Guskov P.M. // IEEE Conference 2017 Dynamics of Systems, Mechanisms and Machines (Omsk, 2017.
10. Steffens Karl-Georg. The History of Approximation Theory. From Euler to Bernstein / Karl-Georg Steffens. – Boston: Birkhauser, 2006. – 219 p.