ОШИБКИ, ОКАЗЫВАЮЩИЕ ВЛИЯНИЕ НА ПРОЦЕДУРУ ИДЕНТИФИКАЦИИ И МОДЕЛИРОВАНИЯ ДИАГНОСТИРУЕМОЙ СИСТЕМЫ

Волкова О.Р.¹, Саркисова И.О.²

¹ORCID: 0000-0002-2364-5691, кандидат технических наук; ²кандидат технических наук, ФГБОУ ВО «МГТУ «СТАНКИН».

ОШИБКИ, ОКАЗЫВАЮЩИЕ ВЛИЯНИЕ НА ПРОЦЕДУРУ ИДЕНТИФИКАЦИИ И МОДЕЛИРОВАНИЯ ДИАГНОСТИРУЕМОЙ СИСТЕМЫ

Аннотация

Работа посвящена видам ошибок, с которыми сталкиваются исследователи при применении взаимно-корреляционного метода, предложенного Н. Винером при диагностировании высокоэффективных технических систем.

Ключевые слова: идентификация, моделирование, диагностика, функциональные ряды Винера.

Volkova O.R.¹, Sarkisova I.О.²

¹ORCID: 0000-0002-2364-5691, PhD in Engineering, ² PhD in Engineering,

MSTU «STANKIN».

ERRORS THAT AFFECT THE PROCESS OF IDENTIFYING AND MODELING DIAGNOSED SYSTEM

Abstract

The article describes the main types of errors encountered by researchers when using cross-correlation method proposed by N Wiener in diagnosis of highly technical systems.

Key words: identification, modeling, diagnostics, functional series Wiener.

Решение задач оперативной диагностики современных высокоэффективных систем различного назначения невозможно без широкого использования методов математического моделирования. Одной из важнейших проблем при этом является формализованное описание поведения диагностируемой системы соответствующей достоверной математической моделью. В случае недостаточности или отсутствии априорных данных об исследуемой динамической системе предпочтительней оказывается подход, при котором для установления причинно-следственных зависимостей применяются методы идентификации, базирующиеся на оценивании структуры и параметров модели по экспериментальным данным, получаемым при опытных или эксплуатационных испытаниях. Одним из инструментов, реализующим это направление, является подход, который основывается на разложениях выходного процесса диагностируемой технической системы в функциональные ряды ([1], [2]) и позволяет естественным образом интерпретировать результаты его применения в удобных для пользователя терминах. Идея подхода заключается в аппроксимации выхода (построении математической модели)  диагностируемой системы ортогональным рядом Винера:

(1)

где  – ортогональный функционал Винера порядка  – ядро функционала Винера порядка . При этом конструирование модели диагностируемой системы по взаимосвязи между входным и выходным процессам  и  сводится к реализации следующих двух основных этапов:

• определение ядер функционалов в (1) (идентификация характеристик диагностируемой системы);
• конструирование модели исследуемой системы в виде конечной суммы (1) (моделирование реакции (прогноз поведения) диагностируемой системы).

Далее достаточно оценить рассматриваемые функции в условиях, характерных для нормальной работы диагностируемой системы и сравнивать с ними измеряемые зависимости.

Несмотря, что данный подход имеет возможность широкого применения при диагностировании реальных систем различной природы и назначения,  он до сих пор не нашел широкого практического применения. Связано это с рядом экспериментальных трудностей, вызванных технологией вычисления функционалов Винера более высоких порядков, и ошибками применения данного метода. Остановимся более подробно на рассмотрении некоторых ошибок, влияющих на результат диагностирования исследуемых систем. Так как, если иметь в виду ошибки моделирования, которые получаются при построении моделей с помощью рядов из функционалов (1), то они образуются в основном из трех видов погрешностей:

• ошибок в задании вида функционалов;
• ошибок вызванных неточным вычислением ядер;
• вычислительных ошибок, в частности, поскольку реализация моделей осуществляется с применением цифровой техники, то это - ошибки дискретного представления многомерных сверток. Эти ошибки на практике значительно меньше, в сравнении с первыми двумя, поэтому нет необходимости в их детальном рассмотрении в данной статье.

Весьма значительное влияние на результат моделирования оказывает первый вид ошибок, а соответственно, и на результат диагностирования исследуемой системы. Данный вид ошибок при построении моделей с помощью взаимно-корреляционного метода идентификации вызван нарушением ортогональности -функционалов. Это связано с тем, что выражения для ортогональных функционалов в виде, предложенным в [1] или [2], справедливы только при идеальном «белом шуме» на входе. На практике же используются сигналы, отличные от «белого шума», что приводит к тому, что функционалы в представлении (1) не являются ортогональными (рис.1а). А, следовательно, необоснованное применение выражений для функционалов является основным источником грубых ошибок при вычислении ядер и построении моделей. Однако если при идентификации исследуемого объекта использовать метод [3], основанный на построении ортогональных функционалов относительно применяемого тестирующего воздействия [4] (рис.1б), то появление ошибок вызванных нарушением ортогональности практически полностью исключается. Причем сама процедура ортогонализации осуществляется непосредственно при вычислении ядер.

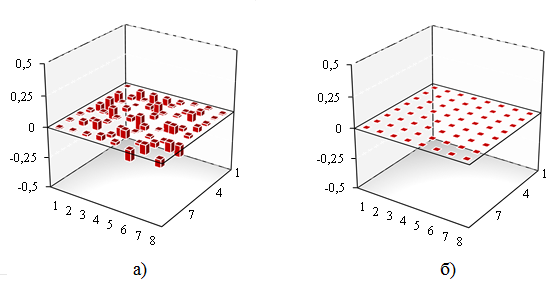
Рис.1 - Оценка АКФ 3-го порядка сигнала, подаваемого на вход исследуемых моделей: а) сформированного стандартным генератором СП, б) подвергшемуся преобразованию с целью обеспечения ортогональности

На рис.2. приведены зависимости дисперсий ошибки  двух квадратических моделей от количества учитываемых точек в ядрах системы , где первая модель была построена с использованием взаимно-корреляционного метода без дополнительного преобразования построенного сигнала типа «белый шум», а для создания второй модели использовался подход, основанный на построении ортогональных функционалов относительно применяемого тестового воздействия соответствующего сигналу «белый шум».

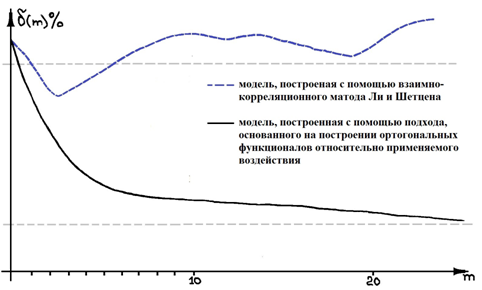
Рис. 2 - Зависимость дисперсии ошибки квадратической модели от количества учитываемых точек в ядрах системы.

Как видно из рисунка, с ростом числа учитываемых точек в ядрах дисперсия ошибки 1-ой модели существенно возрастает, а для второй модели она уменьшается, становясь практически постоянной, после того как число точек в ядре охватило всю память системы.

Второй тип ошибок, который оказывает влияние на результат моделирования с помощью рядов из функционалов, связан непосредственно с самим процессом вычисления ядер диагностируемой системы.

Среднеквадратическую ошибку произведенного моделирования. Пусть исследуемая система носит квадратический характер. Тогда её выходной сигнал при воздействии  можно представить в виде:

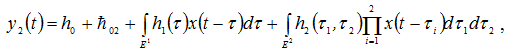(2)

где  – набор ядер, соответствующий диагностируемой системе.

Допустим, что в результате проведения процедуры идентификации экспериментально вычислен набор ядер . Тогда построенная по этому набору модель исследуемой системы образует выходной сигнал:

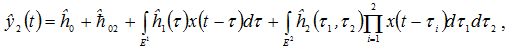Соответственно, среднеквадратическая ошибка произведенного моделирования с учетом, что входное воздействие  является идеальным "белым" гауссовским шумом, определяется выражением вида:

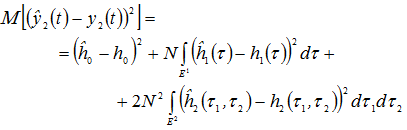(3)

В общем случае определяется в виде для входного сигнала в виде идеального "белого" шума среднеквадратическая ошибка моделирования:

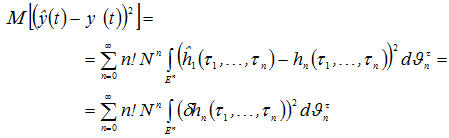(4)

зависит от квадрата рассогласования  между оцененными и истинными значениями ядер.

Из выше сказанного следует, что точность искомых динамических характеристик диагностируемой системы во многом определяется требованиями к параметрам формируемого входного сигнала и к правильной организации самой процедуры идентификации:

• проведение предварительного тестирования системы сигналом специального вида с целью: уточнения интервала дискретности по времени как для входного, так и выходного сигнала, определения полосы пропускания и глубины памяти системы, порядка нелинейности и стационарности процессов, протекающих в системе;
• на основе полученных предварительных данных с помощью сформированного случайного процесса, отвечающего требованиям сигнала «белый шум», определение соответствующих диагностируемой системе набора ядер функционалов Винера и степени адекватности полученных характеристик реальному объекту.

Список литературы / References

1. Винер Н. Нелинейные задачи в теории случайных процессов/ Н. Винер. – М. Изд-во иностранной литературы, 1961 – 159с.
2. Ли Ю.В., Шетцен М. Определение ядер Винера-Хопфа для нелинейных систем методом взаимной корреляции/ Ю.В. Ли, М. Шетцен // В сб. Техническая кибернетика за рубежом. М.: Машиностроение, 1968. - 278 с.
3. Волков Н.В. Функциональные ряды в задачах динамики автоматизированных систем/ Н.В. Волков - М.: Янус-К., 2001. – 100 c.
4. Соломенцев Ю.М., Волков Н.В., Волкова О.Р. Конструирование моделей СП с заданными свойствами методом Винера для идентификации динамических систем/ Ю.М. Соломенцев, Н.В. Волков, О.Р. Волкова // -  ИТ и ВС РАН – 2005. – №3. – С.36-46
5. Дейч А.М. Методы идентификации динамических объектов/ А.М. Дейч – М.: Энергия, 1979.- 240 с.

Список литературы на английском языке / References in English

1. Wiener N.. Nelinejnye zadachi v teorii sluchajnyh processov [NelineNonlinear problems in the theory of random processes]/ N. Wiener - M. Publishing House of Foreign Literature, 1961 – 159 р. [in Russian]
2. Li Ju.V., M. Stetcen. Opredelenie jader Vinera-Hopfa dlja nelinejnyh sistem metodom vzaimnoj korreljacii [Defining of the cross-correlation method core Wiener-Hopf for nonlinear systems]/ Ju.V. Li, M. Stetcen // V sb. Tehnicheskaja kibernetika za rubezhom [Тhe collection Tech. Cybernetics overseas] – M.: Engineering, 1968. – 278 р. [in Russian]
3. Volkov N.V. Funkcional'nye rjady v zadachah dinamiki avtomatizirovannyh system [Functional series in the problems of the dynamics of automated systems]/ N.V. Volkov. – M. Janus-K, 2001. -. 100 р. [in Russian]
4. Solomentsev Y.M., Volkov N.V., Volkova O.R. Konstruirovanie modelej SP s zadannymi svojstvami metodom Vinera dlja identifikacii dinamicheskih system [Construction of models of random processes with specified properties by the Wiener method for the identification of dynamical systems]/ Y.M. Solomentsev, N.V. Volkov, O.R. Volkova// – IT i VS RAN [IT and CS the RAS] – 2005. – №3. – P. 36-46  [in Russian]
5. Dejch A.M. Metody identifikacii dinamicheskih obektov [Methods of identification of dynamic objects]/ Dejch A.M. – M .: Jenergija, 1979.- 240 p. [in Russian]