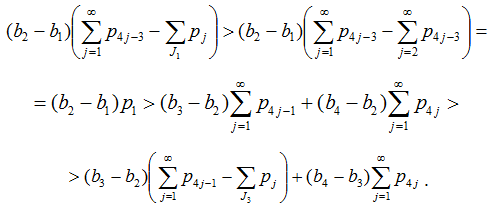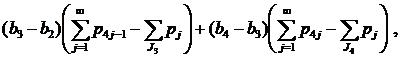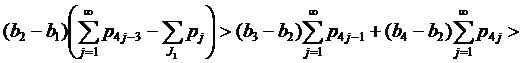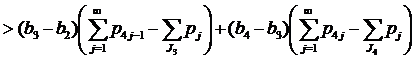НОВЫЙ МЕТОД ПРЕОБРАЗОВАНИЯ СИСТЕМ НЕРАВЕНСТВ ДЛЯ НАХОЖДЕНИЯ ИНТЕРПОЛЯЦИОННЫХ МАРТИНГАЛЬНЫХ МЕР
Шамраева В.В.
ORCID: 0000-0003-0858-7793,
Доцент, кандидат физико-математических наук,
Донской государственный технический университет
Данная работа выполнена при финансовой поддержке РФФИ (проекты 16-07-00888 А, 16-01-00184 А).
НОВЫЙ МЕТОД ПРЕОБРАЗОВАНИЯ СИСТЕМ НЕРАВЕНСТВ ДЛЯ НАХОЖДЕНИЯ ИНТЕРПОЛЯЦИОННЫХ МАРТИНГАЛЬНЫХ МЕР
Аннотация
Для одношаговой модели стохастического базиса рассматривается случайный процесс ![]() , где
, где ![]() — тривиальная
— тривиальная ![]() -алгебра, а
-алгебра, а ![]() —
— ![]() -алгебра, порождённая счётным числом атомов. Предполагается, что
-алгебра, порождённая счётным числом атомов. Предполагается, что ![]() принимает четыре различных значения
принимает четыре различных значения ![]() , причём
, причём ![]() (данный процесс допускает бесконечное множество мартингальных мер). В статье исследуются такие мартингальные меры, которые удовлетворяют ослабленному условию несовпадения барицентров (ОУНБ) - условию, которое позволяет относительно произвольной интерполирующей специальной хааровской фильтрации с помощью такой мартингальной меры интерполировать неполный рынок до полного.
(данный процесс допускает бесконечное множество мартингальных мер). В статье исследуются такие мартингальные меры, которые удовлетворяют ослабленному условию несовпадения барицентров (ОУНБ) - условию, которое позволяет относительно произвольной интерполирующей специальной хааровской фильтрации с помощью такой мартингальной меры интерполировать неполный рынок до полного.
Автором данной статьи представлен новый метод доказательства существования интерполяционных мартингальных мер. Он основан на замене сложных неравенств из ОУНБ, содержащих различные неопределенные подмножества из множества натуральных чисел, более простыми неравенствами, содержащими конкретные компоненты мартингальных мер. Получены достаточные условия на рыночные параметры, которые обеспечивают существование такой мартингальной меры.
Полученные результаты могут быть положены в основу алгоритма и программного комплекса. Такой комплекс позволит применять метод специальных хааровских интерполяций к расчётам на безарбитражных финансовых рынках, что существенно облегчит выбор оптимальных стратегий инвесторов на финансовых рынках.
Ключевые слова: финансовый рынок, мартингальная мера, счётное число состояний, ослабленное условие несовпадения барицентров, полнота, самофинансируемый портфель, полный капитал, платёжное обязательство, интерполирующая фильтрация.
Shamraeva V.V.
ORCID: 0000-0002-1825-0097, Associate professor, PhD in Physics and Mathematics,
Don State Technical University in Rostov-on-Don
A NEW METHOD TO TRANSFORM SYSTEMS OF INEQUALITIES TO FIND THE INTERPOLATION OF MARTINGALE MEASURES
Abstract
For one-step model of stochastic basis a random process ![]() is considered where
is considered where ![]() is a trivial
is a trivial ![]() -field, and
-field, and ![]() is a
is a ![]() -field generated by a countable number of atoms. It is assumed that
-field generated by a countable number of atoms. It is assumed that ![]() takes four different values
takes four different values ![]() , where either
, where either ![]() (this process admits an infinite number of martingale measures). This article takes up such martingale measures that satisfy the weakened noncoincidence barycenter condition (WNBC), - condition that makes it possible to interpolate with such martingale measure incomplete market to completel with respect to arbitrary interpolating special Haar filtering.
(this process admits an infinite number of martingale measures). This article takes up such martingale measures that satisfy the weakened noncoincidence barycenter condition (WNBC), - condition that makes it possible to interpolate with such martingale measure incomplete market to completel with respect to arbitrary interpolating special Haar filtering.
A new method of proof of the existence of the interpolation martingale measures is presented in the article. It is based on the replacement of complex inequalities of the WNBC that contains various undefined subsets of the set of natural numbers, into more simple inequalities containing specific components of martingale measures. In this article we obtain sufficient conditions on market parameters, which ensure the existence of a martingale measure.
The obtained results can be the basis for the algorithm and software complex. The program based on the method will allow to apply special Haar interpolations method to the calculations on the arbitrage-free financial markets, which will greatly facilitate the choice of optimal strategies of investors in the financial markets.
Keywords: financial market; martingale measure; infinite number of buyers-up of stocks, weakened noncoincidence barycenter condition; completeness; self-financing portfolio; capital of portfolio; contingent claim; interpolating filtration.
Рассмотрим одношаговый (B,S)-рынок, заданный на ![]() , где
, где ![]() — одношаговая фильтрация, причём
— одношаговая фильтрация, причём ![]() , а
, а ![]() порождена разбиением
порождена разбиением ![]() на счетное число атомов
на счетное число атомов ![]() ,
, ![]() . Рассмотрим F-адаптированный случайный процесс Z=
. Рассмотрим F-адаптированный случайный процесс Z=![]() , который мы мыслим как дисконтированную стоимость акции. Обозначим через
, который мы мыслим как дисконтированную стоимость акции. Обозначим через ![]() множество невырожденных мартингальных мер этого рынка, совпадающее с множеством решений следующей системы (где
множество невырожденных мартингальных мер этого рынка, совпадающее с множеством решений следующей системы (где ![]() ):
):
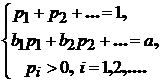 |
(1) |
Для разрешимости системы (1) предположим, что ![]() . В этом случае исходный финансовый рынок безарбитражен. Неполнота данного рынка очевидна. Мартингальные меры неполного рынка, порождают открытый интервал справедливых цен платежного обязательства. Среди них, в случае счетного вероятностного пространства для большого числа (B,S)-рынков существуют интерполяционные мартингальные меры, порождающие "более справедливые" цены. При помощи процедуры хеджирования платежного обязательства, использующей интерполяцию неполного безарбитражного рынка полным рынком (метод хааровских интерполяций), можно определять эволюцию капиталов некоторых финансовых обязательств и рассчитывать компоненты соответствующих реплицирующих самофинансируемых портфелей ([1], [2] и [3]).
. В этом случае исходный финансовый рынок безарбитражен. Неполнота данного рынка очевидна. Мартингальные меры неполного рынка, порождают открытый интервал справедливых цен платежного обязательства. Среди них, в случае счетного вероятностного пространства для большого числа (B,S)-рынков существуют интерполяционные мартингальные меры, порождающие "более справедливые" цены. При помощи процедуры хеджирования платежного обязательства, использующей интерполяцию неполного безарбитражного рынка полным рынком (метод хааровских интерполяций), можно определять эволюцию капиталов некоторых финансовых обязательств и рассчитывать компоненты соответствующих реплицирующих самофинансируемых портфелей ([1], [2] и [3]).
Для одношаговых (B,S)-рынков рассмотрим мартингальные меры, удовлетворяющие ослабленному условию несовпадения барицентров - условию, которое позволяет относительно произвольной интерполирующей специальной хааровской фильтрации с помощью такой мартингальной меры интерполировать неполный рынок до полного.
Определение 1. Мера P∈![]() удовлетворяет ослабленному условию несовпадения барицентров (ОУНБ), если ∀i=1,2,… и для любого набора индексов J⊂{1,2,…}\{i} такого, что дополнение
удовлетворяет ослабленному условию несовпадения барицентров (ОУНБ), если ∀i=1,2,… и для любого набора индексов J⊂{1,2,…}\{i} такого, что дополнение ![]() множества J конечно, выполняется неравенство:
множества J конечно, выполняется неравенство:
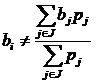 |
(2) |
В [4]-[5] доказывается, что существуют мартингальные меры (при некоторых условиях на такие меры), удовлетворяющие ОУНБ.
Далее будет описан новый метод доказательства существования интерполяционных мартингальных мер, отличный от метода работ [6] и [7]. Этот метод позволит получать результаты, более общие, чем в [6]-[7] . Он основан на замене сложных неравенств из ОУНБ, содержащих различные неопределенные подмножества из множества натуральных чисел, более простыми неравенствами, содержащими конкретные компоненты мартингальных мер. Один из таких результатов сформулирован в [8]-[9].
Определение 2. Будем говорить, что число b, входящее в последовательность {b1, b2,…}, имеет кратность m (m может быть как конечно, так и бесконечно), если в этой совокупности оно присутствует m раз.
Пусть J1⊂{4j-3, j=1,2,3,…}, J2⊂{4j-2, j=1,2,3,…}, J3⊂{4j-1, j=1,2,3,…} и J3⊂{4j, j=1,2,3,…} – произвольные конечные множества.
Лемма 1. Пусть множество ![]() состоит из четырех различных чисел
состоит из четырех различных чисел ![]() , каждое из которых имеет бесконечную кратность. Тогда мера P∈
, каждое из которых имеет бесконечную кратность. Тогда мера P∈![]() удовлетворяет ОУНБ ⇔
удовлетворяет ОУНБ ⇔
| |
(3) (4) |
или
| |
(5) (6) |
Замечание 1. Перечислим всевозможные случаи наполнения множеств J1, J2, J3, J4:
- 1) J1=Ø, J2=Ø, J3=Ø, J4=Ø; 2) J1=Ø, J2=Ø, J3=Ø, J4≠Ø; 3) J1=Ø, J2=Ø, J3≠Ø, J4=Ø; 4) J1=Ø, J2=Ø, J3≠Ø, J4≠Ø - проверка ОУНБ не требуется ((5)-(6) выполнены автоматически);
- 5) J1=Ø, J2≠Ø, J3=Ø, J4=Ø; 6) J1=Ø, J2≠Ø, J3=Ø, J4≠Ø; 7) J1=Ø, J2≠Ø, J3≠Ø, J4=Ø; 8) J1=Ø, J2≠Ø, J3≠Ø, J4≠Ø - требуется проверить неравенства (6) ( (5) выполняются автоматически);
- 9) J1≠Ø, J2=Ø, J3=Ø, J4=Ø; 10) J1≠Ø, J2=Ø, J3=Ø, J4≠Ø; 11) J1≠Ø, J2=Ø, J3≠Ø, J4=Ø; 12) J1≠Ø, J2=Ø, J3≠Ø, J4≠Ø; 13) J1≠Ø, J2≠Æ, J3=Ø, J4=Ø; 14) J1≠Ø, J2≠Ø, J3=Ø, J4≠Ø; 15) J1≠Ø, J2≠Ø, J3≠Ø, J4=Ø; 16) J1≠Ø, J2≠Ø, J3≠Ø, J4≠Ø - Требуется проверить неравенства (5)-(6).
Предложение 1. Пусть множество ![]() состоит из четырех различных чисел
состоит из четырех различных чисел ![]() , каждое из которых имеет бесконечную кратность. Тогда мера P∈
, каждое из которых имеет бесконечную кратность. Тогда мера P∈![]() удовлетворяет ОУНБ ⇔
удовлетворяет ОУНБ ⇔
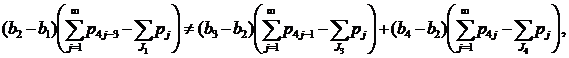 (7)
(7)
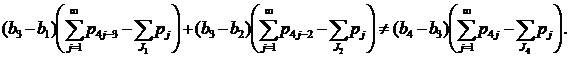 (8)
(8)
Лемма 2 (достаточные условия существования мартингальной меры, удовлетворяющей ОУНБ). Пусть множество ![]() состоит из четырех различных чисел
состоит из четырех различных чисел ![]() , каждое из которых имеет бесконечную кратность и b1<a<b2<b3<b4. Если ∀ k≥1
, каждое из которых имеет бесконечную кратность и b1<a<b2<b3<b4. Если ∀ k≥1
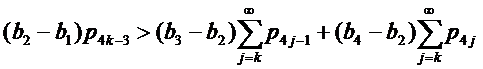
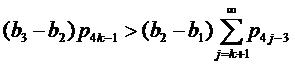 |
(9) (10) |
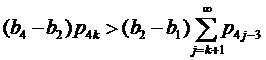 |
(11) |
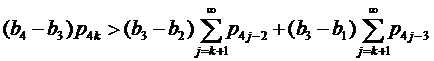 , , |
(12) |
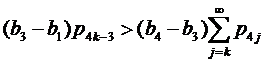 |
(13) |
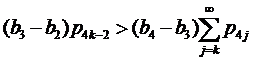 |
(14) |
то мера P∈![]() удовлетворяет ОУНБ
удовлетворяет ОУНБ
Доказательство.
Проверим неравенства (6) для случаев 5)-8) из замечания 1. Эти неравенства равносильны неравенствам (8).
- Пусть J1=∅, J2≠∅, J3=∅, J4=∅ (случай 5) из замечания 1). Неравенства (8) в этом случае имеют вид
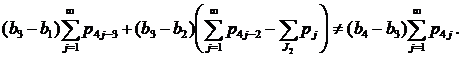 |
(15) |
Поскольку (применили (13) )
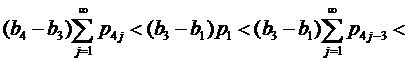
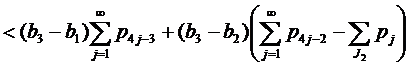 ,
,
то (15) выполнено.
- Пусть J1=∅, J2≠∅, J3=∅, J4≠∅ (случай 6) из замечания 1). Неравенства (8) в этом случае имеют вид
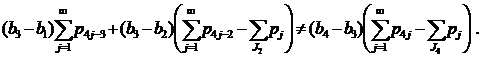 |
(16) |
Поскольку , то действуя так же, как и при доказательстве неравенства (15), получим нужное.
- Пусть J1=∅, J2≠∅, J3≠∅, J4=∅ (случай 7) из замечания 1). Неравенства (8) в этом случае имеют вид (15) и доказываются аналогично.
- Пусть J1=∅, J2≠∅, J3≠∅, J4≠∅ (случай 8) из замечания 1). Неравенства (8) в этом случае имеют вид (16) и доказываются аналогично.
Для остальных случаев будем проверять неравенства (5) и (6). Эти неравенства равносильны (7) и (8) соответственно.
- Пусть J1≠∅, J2=∅, J3=∅, J4=∅ (случай 9) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
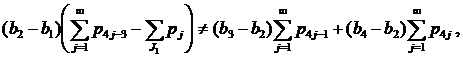 |
(17) |
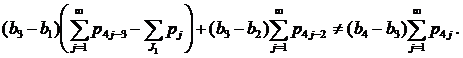 |
(18) |
а) Покажем выполнение неравенств (17).
Если 1∉J1, то применяя (9) при k=1, имеем
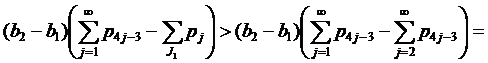
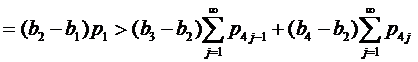
Следовательно, неравенства (17) выполняются.
Если 1∈J1, то применяя (11), имеем
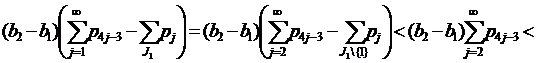
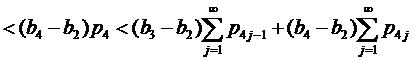 .
.
И в этом случае (17) также выполняются.
б) Покажем выполнение неравенств (18).
Применяя (14), имеем
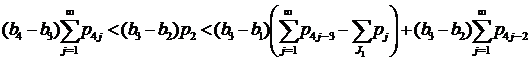 ,
,
что и показывает выполнение (18).
- Пусть J1≠∅, J2=∅, J3=∅, J4≠∅ (случай 10) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
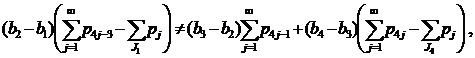 |
(19) |
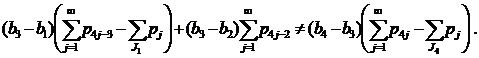 |
(20) |
а) Покажем выполнение неравенств (19).
Если 1∉J1, то применяя (9) при k=1, имеем
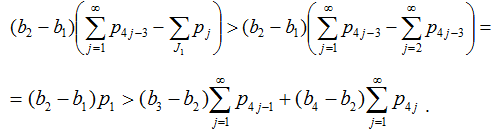 |
(21) |
Значит неравенства (19) выполнены.
Если 1∈J1, то применяя (10), имеем
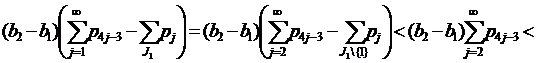
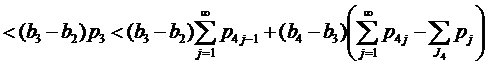 .
.
И в этом случае (19) также выполняются.
б) Поскольку
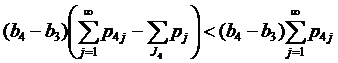 ,
,
выполнение неравенств (20) доказывается аналогично п.5.-б).
- Пусть J1≠∅, J2=∅, J3≠∅, J4=∅ (случай 11) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
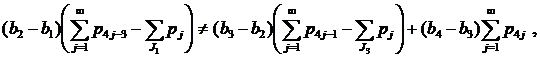 |
(22) |
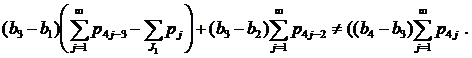 |
(23) |
а) Покажем выполнение неравенств (22).
Если 1∉J1, то применяя (9) при k=1, имеем
|
|
Если 1∈J1, то применяя (11), имеем
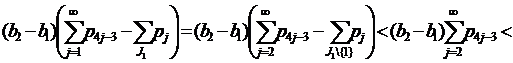
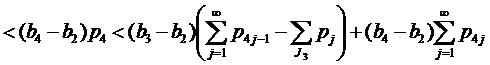
Следовательно (22) выполняются.
б) Выполнение неравенств (23) доказывается аналогично п.5.-б).
- Пусть J1≠Æ, J2=Æ, J3≠Æ, J4≠Æ (случай 12) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
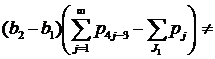
|
(24) |
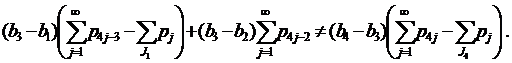 |
(25) |
а) Покажем выполнение неравенств (24).
Если 1∉J1, то применяя (21), получим нужное:
|
|
Если 1∈J1, но 3∉J3, применяя (10), имеем
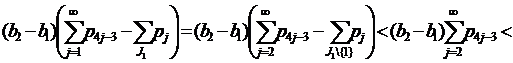
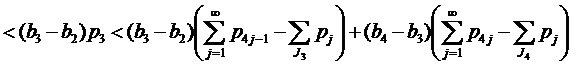 .
.
Если 1∈J1, 3∈J3, но 4∉J4, применяя (11), имеем
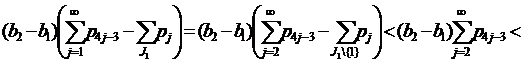
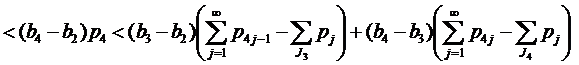
Если 1∈J1, 3∈J3, 4∈J4, но 5∉J1, применяя (9) при k=2, имеем
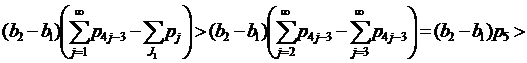
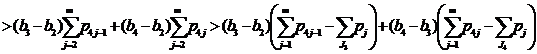 .
.
Продолжаем этот процесс до тех пор, пока мощность одного из множеств J1, J3 или J4 не станет равной нулю.
Таким образом, неравенства (24) выполняются.
б) Выполнение неравенств (25) доказывается аналогично п.6.-б).
- Пусть J1≠∅, J2≠∅, J3=∅, J4=∅ (случай 13) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
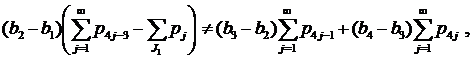 |
(26) |
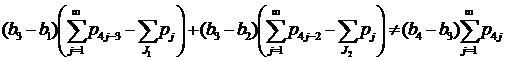 |
(27) |
а) Выполнение неравенств (26) доказывается аналогично п.5.-а).
б) Покажем выполнение неравенств (27).
Если 2∉J2, то применяя (14), получим нужное:
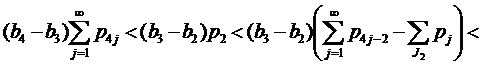
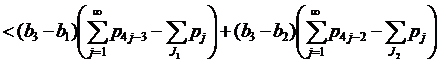 .
.
Если 2∈J2, но 1∉J1, применяем (13) при k=1,
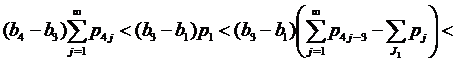
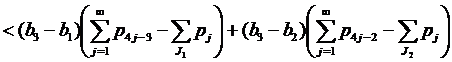 .
.
Если 2∈J2 и 1∈J1, применяем (12) при k=1,
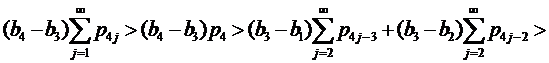
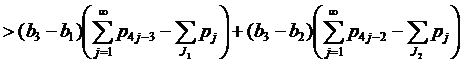
Итак, неравенства (27) выполняются.
- Пусть J1≠Ø, J2≠Ø, J3=Ø, J4≠Ø (случай 14) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
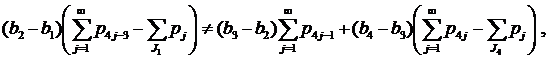 |
(28) |
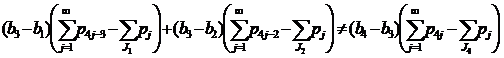 |
(29) |
а) Выполнение неравенств (28) доказывается аналогично п.6.-а).
б) Покажем выполнение неравенств (29).
Если 2∉J2, то применяя (14) при k=1, получим нужное:
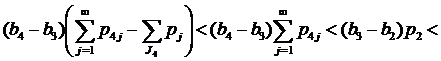
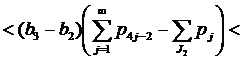
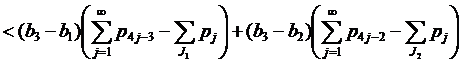 .
.
Если 2∈J2, но 1∉J1, применяем (13) при k=1,
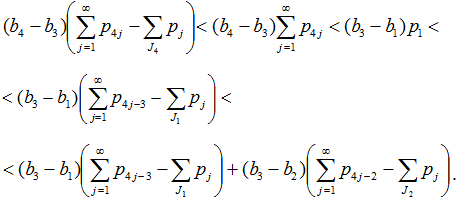
Если 2∈J2 и 1∈J1, но 4∉J4, применяем (12) при k=1,
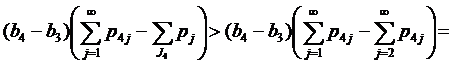
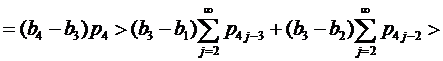
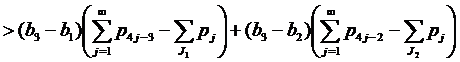
Если 2∈J2, 1∈J1, 4∈J4, но 6∉J2, то применяя (14) при k=2, имеем
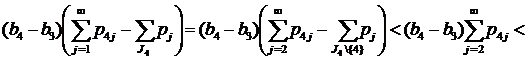
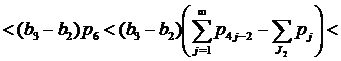
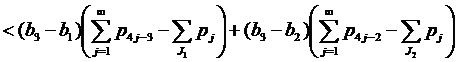 .
.
Если 2∈J2, 1∈J1, 4∈J4, 6∈J2, но 5∉J1, то применяя (13) при k=2, имеем
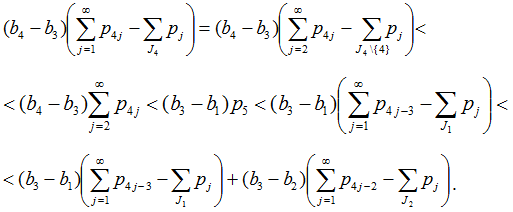 .
.
Если 2∈J2, 1∈J1, 4∈J4, 6∈J2, 5∈J1, но 8∉J4, то применяя (12) при k=2, имеем
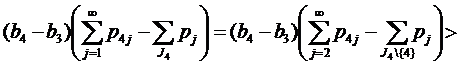
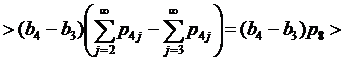
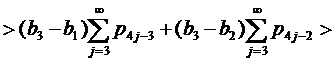
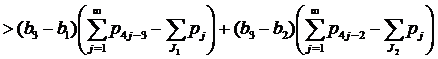
Продолжаем этот процесс до тех пор, пока мощность одного из множеств J1, J2 или J4 не станет равной нулю.
Таким образом, неравенства (29) выполняются.
- Пусть J1≠Ø, J2≠Ø, J3≠Ø, J4=Ø (случай 15) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
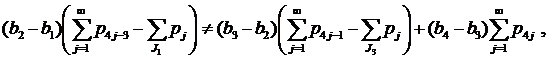 (30)
(30)
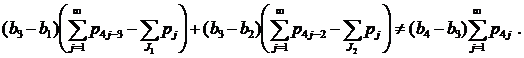 (31)
(31)
а) Выполнение неравенств (30) доказывается аналогично п.7.-а).
б) Выполнение неравенств (31) доказывается аналогично п.9.-б).
- Пусть J1≠Ø, J2≠Ø, J3≠Ø, J4≠Ø (случай 16) из замечания 1). Неравенства (7)-(8) в этом случае имеют вид
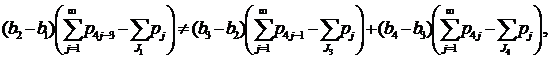 |
(7) |
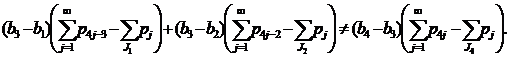 |
(8) |
а) Выполнение неравенств (7) доказывается аналогично п.8.-а).
б) Выполнение неравенств (8) доказывается аналогично п.10.-б).
Лемма 2 доказана.
Лемма 3. Пусть множество ![]() состоит из четырёх различных чисел
состоит из четырёх различных чисел ![]() , каждое из которых имеет бесконечную кратность и
, каждое из которых имеет бесконечную кратность и ![]() . Тогда ОУНБ непусто в
. Тогда ОУНБ непусто в ![]() .
.
Доказательство.
Покажем, что множество мартингальных мер, удовлетворяющих (9)-(14), непустое. Запишем систему (1) следующим образом:
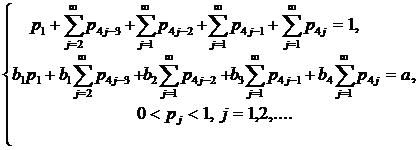 |
(32) |
Построим такую меру ![]() , что выполнено (9)-(14). Возьмём
, что выполнено (9)-(14). Возьмём ![]() ,
, ![]() c>0, d>0– некоторые числа.
c>0, d>0– некоторые числа.
Перепишем систему (32) с введёнными мерами ![]() . Получим систему двух уравнений относительно неизвестных с и d:
. Получим систему двух уравнений относительно неизвестных с и d:
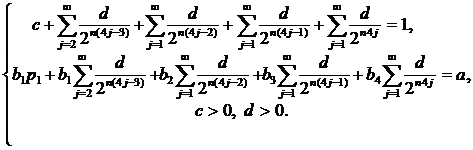 |
(33) |
Так как ![]() , то
, то
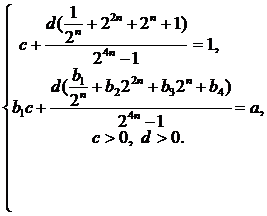 |
(34) |
Найдём решение системы (34). Для этого подсчитаем
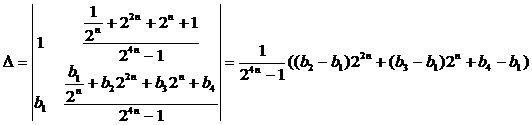 ;
;
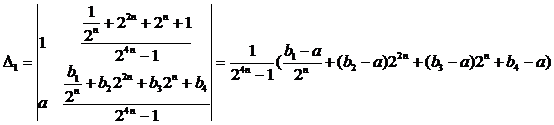 ;
;
![]() .
.
Таким образом,
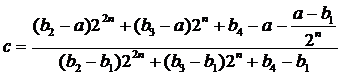 ;
;
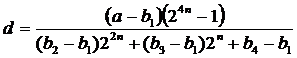 .
.
Следовательно, мы получили невырожденную мартингальную меру ![]() . Проверим, что так построенная мартингальная мера удовлетворяет ОУНБ. Для этого проверим условия (9)-(14) леммы 3.
. Проверим, что так построенная мартингальная мера удовлетворяет ОУНБ. Для этого проверим условия (9)-(14) леммы 3.
Проверим условие (9), а именно
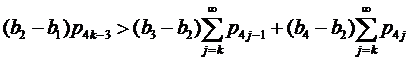
Если k=1, то
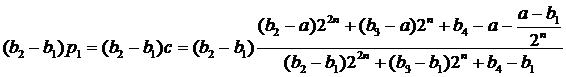
и
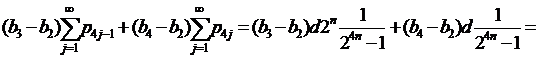
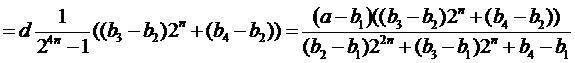 .
.
Значит
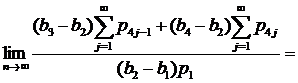
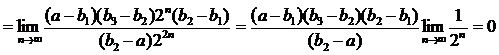
и (9) при k=1 выполняется.
Для k≥2 имеем 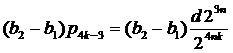 и, учитывая, что
и, учитывая, что 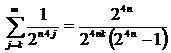 ,
,
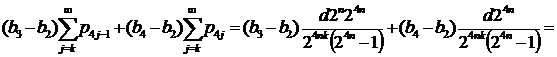
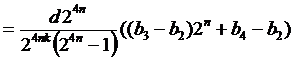 .
.
Значит
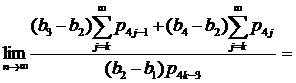
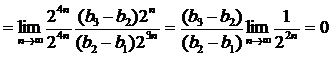
и (9) при ≥2 выполняются.
Проверим условия (10) и (11), а именно 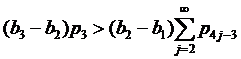 и
и 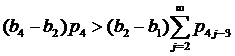 соответственно.
соответственно.
Имеем 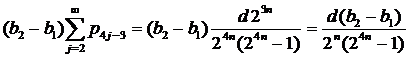 , а
, а
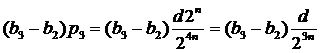 и
и 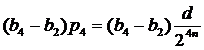 .
.
Значит
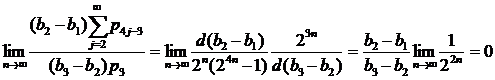
и
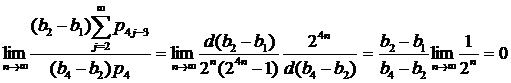 ,
,
что означает выполнение соответственно (10) и (11).
Проверим условия (12) (k≥1), а именно
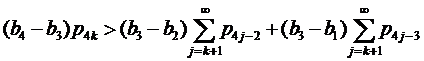 .
.
Так как ![]() и, учитывая, что ,
и, учитывая, что ,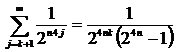
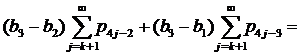
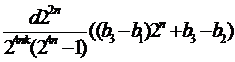 ,
,
то
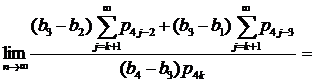
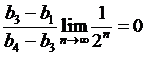 .
.
Значит условия (12) выполняются.
Проверим условия (13) и (14) (k≥1), а именно 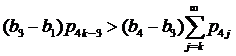 и
и 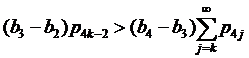 соответственно.
соответственно.
Имеем 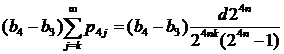 (k≥1), а
(k≥1), а
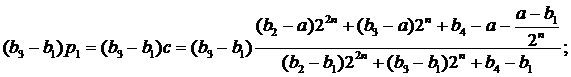
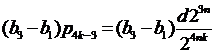 (k≥2);
(k≥2); 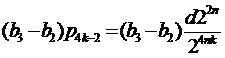 (k≥1).
(k≥1).
Значит
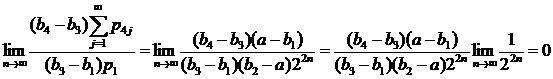 ,
,
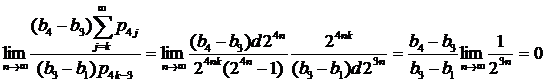 ,
,
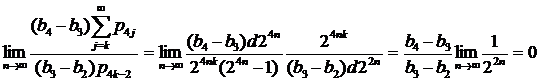 ,
,
что означает выполнение соответственно (13) и (14).
Таким образом, все неравенства леммы 3 выполняются и, следовательно, построенная мера удовлетворяет ОУНБ (ОУНБ непусто).
Лемма 3 доказана.
Заключение
Полученные результаты могут быть положены в основу алгоритма и программного комплекса. Такой комплекс позволит применять метод специальных хааровских интерполяций к расчётам на безарбитражных финансовых рынках, что существенно облегчит выбор оптимальных стратегий инвесторов на финансовых рынках. Один из таких алгоритмов, использующий результаты [4]-[5] описан в [10].
Список литературы / References
- Павлов И.В., Цветкова И.В., Шамраева В.В. Хеджирование одношаговых (В, S) -рынков с бесконечным числом состояний с помощью хааровских интерполяций. Москва, ООО Редакция журнала «ОПиПМ». - Т. 20. – Вып. 2. - 2013. - C. 151-152.
- Цветкова И.В., Шамраева В.В. Расчёт компонентов хеджирующего портфеля с помощью процедуры хааровской интерполяции [Электронный ресурс] / И.В. Цветкова, В.В. Шамраева // Электронное научное издание «Науковедение: Интернет-журнал» №3 (16) 2013. - URL: http://naukovedenie.ru/PDF/45trgsupdf
- Шамраева В.В. Вычисление компонентов хеджирующего портфеля для некоторых платежных обязательств, заданных в финальный момент времени финансового рынка с бесконечным числом состояний [Электронный ресурс] / В.В. Шамраева // Вестник Московского университета им. С.Ю. Витте. Серия 1: Экономика и управление. - 2014. - № 1. - URL: http://www.muiv.ru/vestnik/pdf/eu/eu_2014_1_40-45.pdf
- Павлов И.В., Цветкова И.В., Шамраева В.В. Некоторые результаты о мартингальных мерах одношаговых моделей финансовых рынков, связанные с условием несовпадения барицентров // Вестник РГУПС. - 2012.- № 3.- С. 177-181.
- Павлов И.В., Цветкова И.В., Шамраева В.В. О существовании мартингальных мер, удовлетворяющих ослабленному условию несовпадения барицентров: конструктивистский подход. Вестник РГУПС. - 2014. - № 4. - С.132-139.
- Цветкова И.В., Шамраева В.В. Исследование модели финансового рынка с бесконечным числом скупщиков акций с помощью аргументов двойственности [Электронный ресурс] / И.В. Цветкова, В.В. Шамраева // Электронное научное издание «Науковедение: Интернет-журнал» №4 (13) 2012. - URL: http://naukovedenie.ru/PDF/84trgsupdf
- Павлов И.В., Цветкова И.В., Шамраева В.В. О существовании мартингальных мер, удовлетворяющих ослабленному условию несовпадения барицентров, в случае счетного вероятностного пространства. ОППМ. - М.: Москва, ТВП. - 2016. - Т.61. - Вып.1. - С.173-181.
- Шамраева В.В. Некоторые интерполяционные свойства мартингальных мер [Электронный ресурс] / В.В. Шамраева // Обозрение прикладной и промышленной математики. Т. 22. – Вып. 1, Москва, ООО Редакция журнала «ОПиПМ». - 2015. - URL: http://tvp.ru/conferen/vsppm16/sham.pdf
- Шамраева В.В. Новый метод построения мартингальных мер, удовлетворяющих ОУНБ, в случае счётного вероятностного пространства [Электронный ресурс] / В.В. Шамраева // «Современные методы и проблемы теории операторов и гармонического анализа и их приложения – VI»: междунар. науч. конф. Ростов н/Д: ДГТУ, 2016. – 164 с. URL: http://otha.sfedu.ru/bitrix/templates/social_s1_conf2016/files/tethis_conf_2016_SFEDU.pdf
- Pavlov I.V., Shamraeva V.V. Algorithms for Approximation of Martingale Measures by Interpolation Martingale Eastern European Scientific Journal October 2015. - №5. - C.124-127.URL: http://www.auris-verlag.de/mediapool/99/990918/data/DOI_10.12851_EESJ201510.pdf
Список литературы на английском языке / References in English
- Pavlov I.V., Tsvetkova I.V., Shamraeva V.V. Khedzhirovanniye odnoshagovykh (В, S)-rynkov s beskonechnym chislom sostoyaniy s pomoshchyu Haarovskikh interpoliatsiy [Hedging of One-Step (B, S) Markets with an Infinite Number of States with the Help of Haar Interpolations.] – Moscow, Ltd. “OPiPM.” – V. 20. – No. 2. – 2013. – P. 151-152. [In Russian]
- Tsvetkova I.V., Shamraeva V.V. Raschet komponentov khedzhiruyushchego portfelia s pomoshchiu protsedury Haarovskoy interpoliatsii [Calculation of Hedging Portfolio Components with the Help of Haar Interpolation Procedure] [Electronic resource] / I.V. Tsvetkova, V.V. Shamraeva // Elektronnoye nauchnoye izdaniye «Naukovedeniye: Internet-zhurnal» [Electronic Scientific Edition “Science Studies: Internet Magazine”] – No.3 (16) 2013. – URL: http://naukovedenie.ru/PDF/45trgsu313.pdf [In Russian]
- Shamraeva V.V. Vychisleniye komponentov khedzhyruyushchego portfelia dlia nekotorykh platezhnykh obiazatelstv, zadannykh v finalnyi moment vremeni finansovogo rynka s beskonechnym chislom sostoyaniy [Calculation of Hedging Portfolio Components for Certain Payment Obligations Specified in Final Moment of Time at Financial Market with an Infinite Number of States] [Electronic resource] / Shamraeva V.V. // Vestnik Moskovskogo universiteta im. S.Y. Vitte. Seriya 1: Ekonomika I upravleniye [Bulletin of Moscow University. S.Y. Witte. Series 1: Economy and Management] – 2014. – No. 1. – URL: http://www.muiv.ru/vestnik/pdf/eu/eu_2014_1_40-45.pdf [In Russian]
- Pavlov I.V., Tsvetkova I.V., Shamraeva V.V. Nekotorye rezultaty o martingalnykh merakh odnoshagovykh modeley finansovykh rynkov, sviazannye s usloviem nesovpadeniya baritsentrov [Certain Results on Martingale Measures in One-Step Models at Financial Markets Associated with the Condition of Barycenters Discrepancy] // Vestnik RGUPS [RSURE Bulletin] – 2012. – No. 3. – P. 177-181. [In Russian]
- Pavlov I.V., Tsvetkova I.V., Shamraeva V.V. O sushchestvovanii martingalnykh mer, udovletvoriayushchikh oslablennomu usloviyu nesovpadeniya baritsentrov: konstruktivistskiy podhod [On Existence of Martingale Measures that Satisfy a Weakened Condition of Barycenters Discrepancy: Constructivist Approach] // Vestnik RGUPS [RSURE Bulletin] – 2014. – No.4. – P. 132-139. [In Russian]
- Tsvetkova I.V., Shamraeva V.V. Issledovaniye modeli finansovogo rynka s beskonechnym chislom skupshchikov aktsiy s pomoshchyu argumentov dvoystvennosti [Study of the Model of Financial Market with an Infinite Number of Shares Buyers with the Help of Duality Arguments] [Electronic resource] / I.V. Tsvetkova, V.V. Shamraeva // Elektronnoe nauchnoye izdaniye «Naukovedeniye: Internet-zhurnal» [Electronic Scientific Edition “Science Studies: Internet Magazine”] – No. 4 (13) 2012. – URL: http://naukovedenie.ru/PDF/84trgsu412.pdf [In Russian]
- Pavlov I.V., Tsvetkova I.V., Shamraeva V.V. O sushchestvovanii martingalnykh mer, udovletvoriayushchikh oslablennomu usloviyu nesovpadeniya baritsentrov v sluchae schetnogo veroyatnostnogo prostranstva. [On Existence of Martingale Measures that Satisfy a Weakened Condition of Barycenters Discrepancy in Case of a Countable Probability Space] - M.: Moscow, OPPM. TVP. – 2016. – V.61. – No.1. – P.173-181. [In Russian]
- Shamraeva V.V. Nekotorie interpoliatsionnye svoystva martingalnykh mer [Interpolation Properties of Martingale Measures] [Electronic resource] / V.V. Shamraeva // Obozreniye prikladnoy i promyshlennoy matematiki [Review of Applied and Industrial Mathematics]. – V. 22. – Iss. 1, Moscow, Ltd. Magazine “OPiPM.” – 2015. – URL:http://tvp.ru/conferen/vsppm16/sham.pdf [In Russian]
- Shamraeva V.V. Noviy metod postroyeniya martingalnykh mer, udovletvoriayushchikh OUNB, v sluchae schetnogo veroyatnostnogo prostransva [New Method of Constructing Martingale Measures Satisfying OUNB in Case of a Countable Probability Space] [Electronic resource] / V.V. Shamraeva // «Sovremennye metody i problem teorii operatorov I garmonisheskogo analiza i ikh prilozheniya – VI» [“Modern Methods and Problems of Operator Theory, Harmonic Analysis and Applications – VI”]: Intern. Scientific. Conf. Rostov n/D: DGTU, 2016. – 164 p. URL: http://otha.sfedu.ru/bitrix/templates/social_s1_conf2016/files/tethis_conf_2016_SFEDU.pdf [In Russian]
- Pavlov I.V., Shamraeva V.V. Algorithms for Approximation of Martingale Measures by Interpolation of Martingale Measures. [Electronic resource] // Eastern European Scientific Journal. – October 2015. – No.5. – P.124-127. URL: O http://www.auris-verlag.de/mediapool/99/990918/data/DOI_10.12851_EESJ201510.pdf