МОДЕЛЬ ОБРАБОТКИ ТВЁРДЫХ ТЕЛ БОРМАШИНОЙ ДЛЯ ХИРУРГИЧЕСКОГО СИМУЛЯТОРА

Алайцев И.К.¹, Данилова Т.В.², Мантуров А.О.³, Мареев Г.О.⁴, Мареев О.В.⁵

¹ORCID: 0000-0003-4657-2701, Аспирант, Саратовский государственный технический университет имени Гагарина Ю.А., ²ORCID: 0000-0003-1986-2244, Кандидат физико-математических наук, доцент, Саратовский государственный технический университет имени Гагарина Ю.А., ³ORCID: 0000-0002-1341-171X, Кандидат физико-математических наук, доцент, Саратовский государственный технический университет имени Гагарина Ю.А., ⁴Доктор медицинских наук, доцент, Саратовский государственный университет имени В.И.Разумовского, ⁵Доктор медицинских наук, профессор, Саратовский государственный университет имени В.И.Разумовского

МОДЕЛЬ ОБРАБОТКИ ТВЁРДЫХ ТЕЛ БОРМАШИНОЙ ДЛЯ ХИРУРГИЧЕСКОГО СИМУЛЯТОРА

Аннотация

Симуляционное обучение с применением средств виртуальной реальности является одним из современных образовательных подходов, в том числе, и в медицине. Важнейшим аспектом в образовании студентов хирургических специальностей является развитие у обучающихся практических навыков, в первую очередь - навыков использования различных хирургических инструментов. При этом на первый план выходят тактильные ощущения, поскольку именно они являются определяющими в работе хирурга. Текущий уровень развития вычислительной техники позволяет создавать системы виртуальной хирургии с тактильной обратной связью, способные воссоздавать не только визуальные, но и тактильные ощущения в ходе симуляции. Одной из задач, решаемых при разработке хирургического симулятора с тактильной обратной связью, позволяющего производить обучение студентов работе с бормашиной, является имитация обработки твёрдых тел, например, костных структур, с удалением материала. В данной статье описана модель имитации удаления материала бормашиной, позволяющая учитывать скорость вращения бора, его форму и свойства поверхности. Описанная модель может быть программно реализована в рамках программного обеспечения симулятора и способна обеспечить высокий уровень реалистичности.

Ключевые слова: виртуальная реальность, моделирование, симуляция, виртуальная хирургия.

Alaytsev I.K.¹, Danilova T.V.², Manturov A.O.³, Mareev G.O.⁴, Mareev O.V.⁵

¹ORCID: 0000-0003-4657-2701, Postgraduate student, Yuri Gagarin Saratov State Technical University, ²ORCID: 0000-0003-1986-2244, PhD in Physics and Mathematics, Associate professor, Yuri Gagarin Saratov State Technical University, ³ORCID: 0000-0002-1341-171X, PhD in Physics and Mathematics, Associate professor, Yuri Gagarin Saratov State Technical University, ⁴MD, Associate professor, Saratov State Medical University named after V. I. Razumovsky, ⁵MD, Professor, Saratov State Medical University named after V. I. Razumovsky

SOLID BODY DRILLING IN VIRTUAL SURGERY SYSTEM

Abstract

Simulation systems application is a modern way for students training in surgery. Most of the existing approaches require specific consumables that are destroyed during training. Thus, the training becomes quite expensive while not providing standardization of training process and making it difficult to rate the quality of skills trained. Exploitation of virtual reality provides much better education standardization capabilities while eliminating the need for consumables and making it possible to semiautomatic rating of training results. Solid body drilling is one of the processes that are simulated in virtual surgery system. The realism of such simulation greatly depends upon the mathematical model used to imitate material erasure. This paper describes a mathematical model that can be used for this kind of simulation and provides high realism.

Keywords: virtual reality, modeling, simulation, virtual surgery.

Одной из задач, решаемых при разработке хирургического симулятора с тактильной обратной связью [3], позволяющего производить обучение студентов работе с бормашиной, является имитация обработки твёрдых тел, например, костных структур, с удалением материала. От реалистичности применяемой модели имитации удаления напрямую зависит общее качество симуляции, а также уровень практических навыков студентов, проходящих обучение: в случае, если применяемая модель обработки костных структур позволяет нереалистичное поведение, то у обучающегося пропадает возможность планирования своих действий. При этом важно, чтобы при имитации работы с бормашиной учитывались не только свойства кости, но и параметры бора: качество, форма, размер, скорость вращения.

Существуют различные подходы к моделированию обработки твёрдых тел. В большинстве своём они развиваются в направлении моделирования работы с металлическими объектами. Наиболее популярный подход заключается в применении метода конечных элементов (МКЭ). Однако, применение МКЭ в рамках системы симуляции сопряжено со значительными трудностями: во-первых, данный метод крайне ресурсоёмок, а все вычисления в системах с обратной связью должны производиться с частотой порядка 1000 Гц, во-вторых, физические свойства костной ткани мало изучены и значительно отличаются от таковых для металла. Таким образом, возникает необходимость в разработке модели, обеспечивающей достаточный уровень реалистичности и требующей достаточно малого, по сравнению с МКЭ, объёма вычислений.

Авторами предлагается математическая модель вычисления материала, удаляемого при соприкосновении бора с моделируемым объектом, учитывающая качество бора, его геометрию, скорость вращения, а также свойства материала моделируемого объекта, пригодная для применения в хирургических симуляторах с тактильной обратной связью. Вычисление происходит в дискретной манере, т.е. при расчёте объёма удаляемого материала используется разбиение пространства на воксели.

Скорость удаления материала зависит от линейной скорости перемещения резца в точке соприкосновения бора с поверхностью объекта. В свою очередь, линейная скорость резца в точке соприкосновения находится в прямой пропорциональной зависимости от радиуса бора в этой точке:

  (1)

где: v – линейная скорость в точке, f – частота вращения, R – расстояние до оси вращения в точке соприкосновения резца с поверхность объекта.    

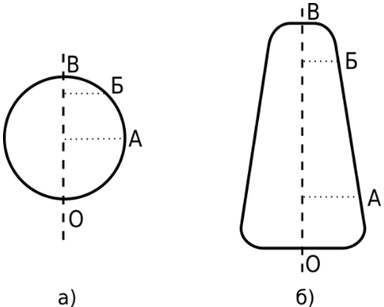
Рис. 1 - Продольные срезы боров

 

На рис. 1 а) схематически изображён сферический бор, на рис. 1 б) изображён бор в форме усечённого конуса. Для обоих вариантов применены одинаковые обозначения:

• О – ось вращения бора
• А – точка на поверхности бора, такая, что расстояние в точке А до оси вращения больше, чем в точке Б;
• Б – точка на поверхности бора;
• В – точка на вершине бора.

С учётом уравнения (1) имеем:

• скорость удаления материала в точке А равна нулю, т.к. линейная скорость данной точки равна нулю, поскольку она лежит на оси вращения;
• скорость удаления материала в точке В больше, чем скорость удаления материала в точке Б, т.к. линейная скорость резца в точке В больше, чем в точке Б, поскольку расстояние до оси вращения в точке В больше, чем в точке Б.

Таким образом, объём удаляемого материала в каждой точке может быть вычислен по формуле:

  (2)

где:

R_i – расстояние до оси вращения бора в точке соприкосновения бора с поверхностью объекта;

γ – коэффициент, определяемый качеством бора;

μ – коэффициент, определяемый свойствами материала, из которого состоит объект.

Кроме формы, важным фактором, влияющим на скорость удаления материала, является качество бора. Выделяют три основных типа боров:

• грубые стальные сферические розеточные боров (steel rosen);
• стальные боры с грубым напылением (gold diamond);
• тонкие алмазные боры (diamond).

Каждый из них характеризуется различной скоростью удаления материала: быстрее всех удаляют материал розеточные боры, в то время, как алмазные боры производят удаление материала крайней медленно.

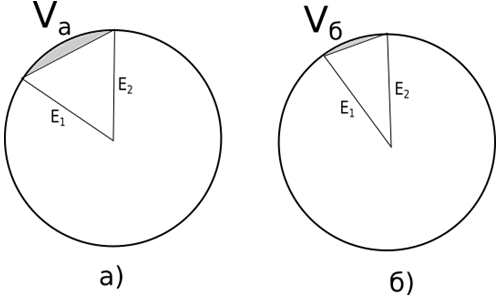
Рис. 2 - Поперечные срезы боров

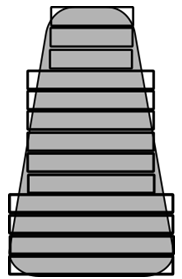
Рис. 3 - Аппроксимация бора

На Рис. 2 изображены поперечные разрезы двух розеточных боров с различным числом режущих граней: бор а) имеет меньшее число режущих граней, в то время, как бор б) имеет большее число режущих граней. Режущие грани обозначены прямыми E₁ и E₂ для обоих боров. Объём материала, удаляемый каждой гранью при совершении одного оборота прямо пропорционален расстоянию между гранями, а значит обратно пропорционален их числу. Как можно видеть, объём V_а, удаляемый каждой гранью бора а), больше, чем объём V_б, удаляемый каждой гранью бора б).

Таким образом, возможно построение уравнения для γ из уравнения (2):

  (3)

где:

h - высота сегмента в точке касания: для упрощения вычислений бор аппроксимируется при помощи цилиндров (Рис. 3);

R – радиус бора в точке касания;

N_E – число режущих граней.

Кроме того, предлагаемая математическая модель, позволяет учитывать качество бора. В рамках модели все боры представляются, как розеточные, с различным числом режущих граней. Из приведённых формул видно, что такое представление допустимо, т.к. отражает картину, наблюдаемую в реальности:

• розеточные боры в модели будут представляться, как розеточные боры с малым числом режущих граней, в результате чего скорость удаления материала ими будет максимальной;
• алмазные боры будут представляться, как розеточные с большим числом режущих граней, в результате чего скорость удаления материала ими будет крайней мала.

Таким образом, с учётом уравнения (3), уравнение (2) примет вид:

  (4)

Свойства материала, описываемые коэффициентом μ, могут быть определены экспериментально, взяты из известных таблиц свойств материалов, либо данный коэффициент может быть подобран эмпирически.

Было произведено сравнение описанной модели удаления с описанными в [1][2]. В отличие от рассмотренных моделей, в которых скорость удаления материала в основном зависела от приложенной силы, в предлагаемой авторами модели общая скорость удаления материала зависит в первую очередь от свойств бора и скорости его вращения. Зависимость от силы давления присутствует, но эта зависимость второстепенна, т.к. даже в случае чрезмерно большого давления скорость удаления материала всегда будет ограничена объёмом, определяемым на основе свойств бора. Сила давления лишь определяет, насколько глубоко возможно продвинуться при удалении максимально возможного объёма: при незначительном давлении углубление инструмента может остановиться до удаления максимально возможного объёма, в то время, как при значительном давлении произойдёт удаление максимально возможного объёма.

Недостатком описанной модели удаления является больший по сравнению с аналогами [1][2] объём необходимых вычислений. Решением данной проблемы является применение параллельных вычислений: поскольку вычисления производятся для каждого вокселя поверхности бора независимо от других, то возможно применение SIMD-вычислений. Кроме того, модель не является абсолютно математически и физически строгой. Однако, данная модель является достаточной для применения в хирургических симуляторах, где на первом месте находятся ощущения пользователя и общий ощущаемый реализм симуляции.

Список литературы / References

1. Morris, D. Haptics and Physical Simulation for Virtual Bone Surgery: PHD thesis / Morris Dan. - Stanford: Stanford University. 2006. - 213 c.
2. Petersik, A. [и др.] Method for the simulation of the haptic of an interaction of a guided object with a virtual three-dimensional object // US Patent. - 2013. 10 с.
3. Алайцев, И.К. [и др.] Разработка программно-аппаратного коплекса оториноларингологического симулятора с тактильной обратной связью / И.К. Алайцев, Т.В. Данилова, Г.О. Мареев, О.В. Мареев // Методы компьютерной диагностики в биологии и медицине - 2015. - 2015. - C. 109–111.

Список литературы на английском языке / References in English

1. Morris, D. Haptics and Physical Simulation for Virtual Bone Surgery: PHD thesis / Morris Dan. - Stanford: Stanford University. 2006. - 213 p.
2. Petersik, A. [et. al.] Method for the simulation of the haptic of an interaction of a guided object with a virtual three-dimensional object // US Patent. - 2013. 10 p.
3. Alaytsev, I.K. [et. al.] Razrabotka programmno-apparatnogo kopleksa otorinolaringologicheskogo simulyatora s taktil'noy obratnoy svyaz'yu [Development of computer appliance of virtual surgey with haptic feedback] / I.K. Alaytsev, T.V.Danilova, A.O.Manturov, G.O. Mareev, O.V. Mareev // Metody komp'yuternoy diagnostiki v biologii i meditsine - 2015 [Methods of Computer Aided diagnostics in Medicine and Biology 2015 Conference Proceedings]. - 2015. - P. 109–111. [in Russian]