МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЖИЛИЩНОГО РЫНКА НЕДВИЖИМОСТИ

Файдрахманова Г.Ф.

ORCID:  0000-0003-0409-3833, Cтарший преподаватель, Башкирский государственный университет, Нефтекамский филиал

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЖИЛИЩНОГО РЫНКА НЕДВИЖИМОСТИ

Аннотация

В статье рассматривается оценка стоимости жилищной недвижимости путем построения регрессионных моделей, на примере оценки стоимости квартир для городов Нефтекамск и Агидель. Определяются существенные факторы, влияющие на цены однокомнатных, двухкомнатных, трехкомнатных и четырехкомнатных квартир городов Нефтекамск и Агидель. Строится математическая модель позволяющая проводить массовую оценку рыночной стоимости объектов жилой недвижимости в общем виде, по которой в дальнейшем можно проводить анализ адекватности модели, строить прогнозы и делать выводы.

Ключевые слова: математическая модель, регрессионный анализ, оценка, стоимость, жилая недвижимость.

Faydrakhmanova G. F.

ORCID:  0000-0003-0409-3833, Senior lecturer, Bashkir state University, Neftekamsk branch

MATHEMATICAL MODELING OF THE HOUSING MARKET REAL ESTATE

Abstract

The article deals with the valuation of residential properties by constructing regression models on the example of estimation of cost of apartments for the cities of Agidel and Neftekamsk. Identified significant factors affecting the prices of one, two, three and four-room apartments of the cities of Agidel and Neftekamsk. Mathematical model allowing to carry out mass valuation of residential real estate in General, on which further analysis can be done of the adequacy of the model to make predictions and draw conclusions.

Keywords: mathematical model, regression analysis, estimation, cost, residential property.

Исследование нацелено на разработку математической модели, позволяющей проводить массовую оценку рыночной стоимости объектов жилой недвижимости на примере выявления и анализа основных факторов, влияющих на цены однокомнатных, двухкомнатных, трехкомнатных, четырехкомнатных квартир городов Нефтекамска и Агидель и [1, С. 69].

Для анализа, вычисления статистических характеристик использовались программы Eviews [3] и Microsoft Exсel [4].

Были построены и проанализированы разные модели зависимости стоимости квартиры от факторов. После результатов корреляционного и регрессионного анализа в результате получили наиболее лучшие модели для г. Нефтекамск (см. формулу (1) или (2)) и г. Агидель (см. формулу (3) или (4)).

Модель для г. Нефтекамск:

                                                   (1)

или

                                                                   (2)

Модель для г. Агидель:

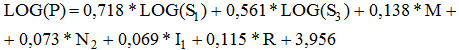                                                                                     (3)

или

                                                                                              (4)

Построенные многофакторные регрессионные модели зависимости стоимости квартиры от различных факторов для г. Нефтекамск и г. Агидель можно записать в общем виде (по формуле (5) или (6)):

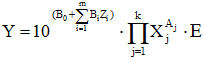                                                                                                                        (5)

или

                                                                                    (6)

где Y – цена анализируемого объекта, В₀ – коэффициент, отражающий влияние на базовую цену объекта, Z_i и X_j – переменные, описывающие ценообразующие факторы [5, С. 55]; B_i – коэффициент, отражающий влияние на цену объекта его качественного признака (ценообразуещего фактора) Z_i; m – количество данных факторов Z_i; A_j – коэффициент, отражающий влияние на цену объекта количественного фактора (например: площадь объекта, площадь кухни, нежилой площади и т.д.) X_j; k – количество данных факторов X_j, Е - ошибка расчетов.

Данная модель в общем виде является мультипликативной регрессионной моделью – внутренне линейной по параметрам. Для расчета её коэффициентов методом наименьших квадратов (МНК), уравнение (5) преобразуется в аддитивный вид (линеаризуется) путем логарифмирования обоих частей (см. формула (7) или (8)):

                      (7)

 или

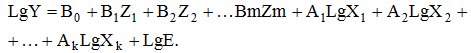                                                                           (8)

Путем замены y=LgY, z₁=Z₁, z₂=Z₂, …, z_m=Z_m, x₁=LgX₁, x₂=LgX₂, ..., x_k=LgX_k, b₀=B₀, b₁=B₁, b₂=B₂, …, b_m=B_m, a₁=A₁, a₂=A₂, …, a_k=A_k, ε =LgE получим линейную регрессионную модель (формула (9) или (10))

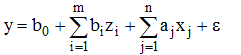                                                                                                     (9)

или

                                                               (10)

Анализируя построенную модель для г. Нефтекамска получены следующие результаты.

Около 78,9% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Значимость уравнения множественной регрессии в целом, проверена на основе F-критерия Фишера (Fрасч=128,5) и гипотезу об адекватности уравнения регрессии принимаем с вероятностью 99%.

Существенность влияния коэффициентов уравнения регрессии при независимых факторах оценивается с использованием t-критерия Стьюдента. На логарифм стоимости квартиры log(p) влияют факторы (по убыванию существенности): логарифм общей площади квартиры (logs₁) (t_расч=25,21), планировка квартиры (u₁) хрущевка (t_расч=-3,54), материал стен (M) кирпич (t_расч=3,28) с вероятностью 99%, материал стен (m) влияет с вероятностью 91%. Если планировка квартиры (u₂) элитная (t_расч=2,55), то соответствующий коэффициент влияет с вероятностью 98,9%, если район (r) окраина (t_расч=-1,76) – с вероятностью 92%, если квартира (n₂) двухкомнатная (t_расч=1,64) – с вероятностью 89,9%, если этаж (i) средний (t_расч=1,41) – с вероятностью 84 %.

 Проверка выполнения условий для получения «хороших» оценок методом наименьших квадратов показала, что ожидание случайной компоненты равно 0 (tрасч=0), дисперсия постоянна (F_расч=2,93 при F_{табл(n1=111;n2=112)}=1,56), ковариация равна 0 (d_расч=1,89 при d₁=1,57 d₂=1,78) с вероятностью 95%, мультиколлинеарность в модели отсутствует, так как коэффициенты корреляции между независимыми факторами по модулю меньше чем 0,4. Откуда делаем вывод, что построенная модель для        г. Нефтекамска адекватна по проверенным показателям с вероятностью 84%.

Анализируя построенную модель для г. Агидель получены следующие результаты.

Около 80,5% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Значимость уравнения множественной регрессии в целом, проверена на основе F-критерия Фишера (F_расч=25,03) и гипотезу о значимости уравнения регрессии принимаем с вероятностью 99%.

Существенность влияния коэффициентов уравнения регрессии при независимых факторах оценивается с использованием t-критерия Стьюдента. На логарифм стоимости квартиры log(P) влияют факторы (по убыванию существенности): логарифм общей площади квартиры (logS₁) (t_расч=5,708), материал стен (M) кирпич (t_расч=3,99), если район (R) не по Комсомольскому бульвару (t_расч=2,92) – с вероятностью 99%, если квартира (N₂) двухкомнатная (t_расч=2,72) – с вероятностью 98,9%, если этаж (I₁) первый (t_расч=2,17) – с вероятностью 96,1%, логарифм площади кухни квартиры (logS₃) (t_расч=2,04) c вероятностью 94,9%.

Проверка выполнения условий для получения «хороших» оценок методом наименьших квадратов показала, что ожидание случайной компоненты равно 0 (t_расч=0) с вероятностью 95%, дисперсия постоянна (F_расч=4,05 при F_{табл(n1=7;n2=7)}=3,79) с вероятностью 95%, ковариация равна 0 (d_расч=2,038 при d₁=1,57 d₂=1,8) с вероятностью 95%, мультиколлинеарность в модели отсутствует так как коэффициенты корреляции между независимыми факторами по модулю меньше чем 0,5. Откуда делаем вывод, что построенная модель для г. Агидель адекватна по проверенным показателям с вероятностью 94,9%.

Итак, обе построенные модели (1) и (3) адекватны с вероятностью 84% для г. Нефтекамск и 94,9% для г. Агидель. Для г. Нефтекамск построена зависимость стоимости квартиры (p, руб.) от факторов: общая площадь, (s₁, м²); материал стен кирпич или панель, (m); двухкомнатная квартира или нет, (n₂); этаж средний или крайний, (i); окраина города или нет, (r); хрущевка или нет, (u₁). Для г. Агидель выявлена зависимость стоимости квартиры (P, руб.) от факторов: общая площадь, (S₁, м²); площади кухни, (S₃, м²); материала стен кирпич или панель, (M); двухкомнатная квартира или нет, (N₂); этаж первый или нет, (I₁); центр города или нет, (R).

В модели (1) для г. Нефтекамск:

• с ростом величины «Логарифма общей площади квартиры (Logs₁)» на одну единицу измерения «Логарифм стоимости квартиры (Logp)» возрастает от 0,684 до 0,799 (в среднем на 0,743) единиц измерения при неизменных остальных факторах с вероятностью 95%. Другими словами, если «Общая площадь квартиры (s1)» увеличится в 10 раз, то «Стоимости квартиры (p)» возрастает в 10^^0,684= 4,826 раз до в 10^^0,799=6,302 раз (в среднем в 10^^0,743=5,515 раз) при неизменных остальных факторах с вероятностью 95%;
• если материал стен (m) кирпич, то «Стоимости квартиры (p)» возрастает в пределах от в 10^^0,011= 1,026 раз до в 10^^0,045=1,108 раз (в среднем в 10^^0,028=1,066 раз) при неизменных остальных факторах с вероятностью 95%;
• если квартира (n₂) двухкомнатная, то «Стоимости квартиры (p)» изменяется в пределах от в 10^^-0,003= 0,993 раз до в 10^^0,035=1,084 раз (в среднем в 10^^0,016=1,037 раз) при неизменных остальных факторах с вероятностью 95%;
• если этаж (i) средний, то «Стоимости квартиры (p)» изменяется в пределах от в 10^^-0,005= 0,989 раз до в 10^^0,029=1,069 раз (в среднем в 10^^0,012=1,028 раз) при неизменных остальных факторах с вероятностью 95%;
• если район (r) окраина, то «Стоимости квартиры (p)» изменяется в пределах от в 10^^-0,055= 0,882 раз до в 10^^0,003=1,007 раз (в среднем в 10^^-0,026=0,942 раз) при неизменных остальных факторах с вероятностью 95%;
• если планировка квартиры (u1) хрущевка, то «Стоимости квартиры (p)» уменьшается в пределах от в 10^^-0,057= 0,877 раз до в 10^^-0,016=0,963 раз (в среднем в 10^^-0,036=0,919 раз) при неизменных остальных факторах с вероятностью 95%;
• если квартира (u₂) элитная, то «Стоимости квартиры (p)» возрастает в пределах от в 10^^0,007= 1,015 раз до в 10^^0,052=1,127 раз (в среднем в 10^^0,029=1,070 раз) при неизменных остальных факторах с вероятностью 95%.

В модели (3) для г. Агидель:

• с ростом величины «Логарифма общей площади квартиры (LogS₁)» на одну единицу измерения «Логарифм стоимости квартиры (LogP)» возрастает от 0,46 до 0,975 (в среднем на 0,718) единиц измерения при неизменных остальных факторах с вероятностью 95%. Другими словами, если «Общая площадь квартиры (S₁)» увеличится в 10 раз, то «Стоимости квартиры (P)» возрастает в 10^^0,46= 2,887 раз до в 10^^0,975=9,434 раз (в среднем в 10^^0,718=5,219 раз) при неизменных остальных факторах с вероятностью 95%;
• с изменением величины «Логарифма площади кухни (LogS₃)» на одну единицу измерения «Логарифм стоимости квартиры (LogP)» изменится от -0,002 до 0,1,123 (в среднем на 0,561) единиц измерения при неизменных остальных факторах с вероятностью 95%. Другими словами, если «Площадь кухни (S₃)» увеличится в 10 раз, то «Стоимости квартиры (P)» возрастает в 10^^-0,02=0,996 раз до в 10^^1,123=13,273 раз (в среднем в 10^^0,561=3,637 раз) при неизменных остальных факторах с вероятностью 95%;
• если материал стен (M) кирпич, то «Стоимости квартиры (P)» возрастает в пределах от в 10^^0,067= 1,168 раз до в 10^^0,209=1,619 раз (в среднем в 10^^0,138=1,375 раз) при неизменных остальных факторах с вероятностью 95%;
• если квартира (N₂) двухкомнатная, то «Стоимости квартиры (P)» изменяется в пределах от в 10^^0,018= 1,042 раз до в 10^^0,128=1,343 раз (в среднем в 10^^0,073=1,183 раз) при неизменных остальных факторах с вероятностью 95%;
• если этаж (I) первый, то «Стоимости квартиры (P)» возрастает в пределах от в 10^^0,004= 1,009 раз до в 10^^0,135=1,365 раз (в среднем в 10^^0,069=1,173 раз) при неизменных остальных факторах с вероятностью 95%;
• если район (R) центр (не Комсомольский бульвар), то «Стоимость квартиры (P)» возрастает в пределах от в 10^^0,034= 1,082 раз до в 10^^0,195=1,568 раз (в среднем в 10^^0,115=1,303 раз) при неизменных остальных факторах с вероятностью 95%.

Можно сделать вывод, что факторы, влияющие на цены квартир и соответственно и сами модели для различных городов разные. Существенные факторы, влияющие на стоимость однокомнатных, двухкомнатных, трехкомнатных, четырехкомнатных квартир городов Нефтекамск и Агидель следующие:

• для г. Нефтекамск: площадь квартиры, материал стен, количество комнат в квартире, этажность, район, планировка квартиры.
• для г. Агидель: площадь квартиры, площадь кухни, материал стен, количество комнат в квартире, этажность, район.

В работе построены многофакторные регрессионные модели оценки стоимости жилой недвижимости для однокомнатных, двухкомнатных, трехкомнатных, четырехкомнатных квартир городов Нефтекамск (модель (2)) и Агидель (модель (4)) на реальных данных, которые адекватны с вероятностью 84% для г. Нефтекамск и 94,9% для г. Агидель.

Зависимость стоимости квартиры от различных факторов для       г. Нефтекамск и г. Агидель в общем виде можно записать по формулам (5) или (6), позволяющие проводить массовую оценку рыночной стоимости объектов жилой недвижимости.

При построении модели оценки стоимости жилой недвижимости по формулам (5) или (6), проверки её адекватности, можно провести анализ:

• если 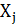 увеличится (уменьшится) в 10 раз, то Y в среднем увеличится (уменьшится) в  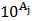раз при неизменных остальных факторах с вероятностью p;
• если 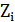 увеличится (уменьшится) единицу, то Y в среднем увеличится (уменьшится) в  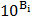раз при неизменных остальных факторах с вероятностью p.

Где Y – цена анализируемого объекта, Z_i и X_j – переменные, описывающие ценообразующие факторы; B_i – коэффициент, отражающий влияние на цену объекта его качественного признака (ценообразуещего фактора) Z_i; m – количество данных факторов Z_i; A_j – коэффициент, отражающий влияние на цену объекта количественного фактора (например: площадь объекта, площадь кухни, нежилой площади и т.д.) X_j; k – количество данных факторов X_j.

Список литературы / References

1. Файдрахманова Г.Ф. Разработка математической модели массовой оценки объектов жилой недвижимости // «Достижения и приложения современной информатики, математики и физики»: материалы II Всероссийской научно-практической заочной конференции (г. Нефтекамск, 17-19 октября 2013 г.). – Уфа: РИЦ БашГУ, 2013. – 94 с. – С. 69-74.
2. Magnus Jan, Peresetsky Anatoly. The price of Moscow apartments // Publishing House "Sinergia PRESS" journal Applied Econometrics. 2010. №1. P.89-105.
3. Молчанов И.Н., Герасимова И.А. Компьютерный практикум по начальному курсу эконометрики (реализация на Eviews): Практикум /Ростовский государственный экономический университет. – Ростов-н/Д., – 2001. – 58 с.
4. Салманов О.Н. Математическая экономика с применением Mathcad и Excel. – СПб.: БХВ-Петербург, 2003. – 464 с.: ил.
5. Цымбаленко С.В., Цымбаленко О.С., Шепель О.В. Особенности определения рыночной стоимости недвижимости муниципальных образований // Оценочная деятельность. 2007. №1. С.55-63.

Список литературы на английском языке / References in English

1. Faydrakhmanova G.F. Razrabotka matematicheskoy modeli massovoy otsenki ob''ektov zhiloy nedvizhimosti [Development of a mathematical model of mass valuation of residential real estate] // «Dostizheniya i prilozheniya sovremennoy informatiki, matematiki i fiziki: materialy II Vserossiyskoy nauchno-prakticheskoy zaochnoy konferentsii (g. Neftekamsk, 17-19 oktyabrya 2013 g.). [«Achievements and applications of contemporary Informatics, mathematics and physics»: proceedings of the II all-Russian scientific-practical conference (city of Neftekamsk, October 17-19, 2013)]– Ufa: RITs BashGU, 2013. – 94 p. – P. 69-74. . [In Russian]
2. Jan Magnus, Anatoly Peresetsky. The price of Moscow apartments // Publishing House "Sinergia PRESS" journal of Applied Econometrics. 2010. No. 1. P. 89-105.
3. Molchanov I.N., Gerasimova I.A. Komp'yuternyy praktikum po nachal'nomu kursu ekonometriki (realizatsiya na Eviews): Praktikum [Computer workshop initial course of econometrics (implementation in Eviews): Workshop] /Rostovskiy gosudarstvennyy ekonomicheskiy universitet [Rostov state economic University] – Rostov-n/D., – 2001. – 58 p. [In Russian]
4. Salmanov O.N. Matematicheskaya ekonomika s primeneniem Mathcad i Excel [Mathematical Economics with the use of Mathcad and Excel] – SPb.: BKhV-Peterburg, 2003. – 464 p.: il. [In Russian]
5. Tsymbalenko S.V., Tsymbalenko O.S., Shepel' O.V. Osobennosti opredeleniya rynochnoy stoimosti nedvizhimosti munitsipal'nykh obrazovaniy [Determination of the market value of the property of municipalities] // Otsenochnaya deyatel'nost' [Appraisal activities]. 2007. №1. P.55-63. . [In Russian]