КЛАССИФИКАЦИЯ И ОПТИМИЗАЦИЯ МНОГОЦЕЛЕВЫХ АЛЬТЕРНАТИВ НА ПРИМЕРЕ ХИМИЧЕСКОГО ПРОИЗВОДСТВА
Двадцатов Р.В.
ORCID 0000-0003-2342-7624,
Аспирант, Санкт-Петербургский Горный Университет
КЛАССИФИКАЦИЯ И ОПТИМИЗАЦИЯ МНОГОЦЕЛЕВЫХ АЛЬТЕРНАТИВ НА ПРИМЕРЕ ХИМИЧЕСКОГО ПРОИЗВОДСТВА
Аннотация
В данной работе рассматривается методика классификации и оптимизации многоцелевых альтернатив на примере химического производства. За основу взяты два направления увеличения надежности производства и снижения стоимости продукции. В работе проводится классификация выбранных альтернатив по алгоритму Ларичева. Составляется таблица доминантных альтернатив. По итогам расчетов выбираются несколько массивов целей. Оптимизация в выбранном массиве альтернатив проводится по трех уровневой шкале. Что позволят увидеть степень значимости альтернатив в выбранном массиве целей.
Ключевые слова: выбор множества альтернатив, многокритериальная оптимизация, экспертная оценка, классификация альтернатив.
Dvadcatov R.V.
ORCID 0000-0003-2342-7624,
Postgraduate student, Saint-Petersburg Mining University
CLASSIFICATION AND OPTIMIZATION OF MULTIFUNCTIONAL ALTERNATIVES TO THE EXAMPLE OF CHEMICAL INDUSTRY
Abstract
In this paper, the technique of classification and optimization of multi-purpose alternatives to the example of the chemical industry. It is based on two lines increase the reliability of production and reducing the cost of production. The work carried out by the classification algorithm selected alternatives Laricheva. Generating tables of dominant alternatives. Following the results of the calculations are selected multiple arrays purposes. Optimization of the selected array of alternatives carried out by the three-level scale. That will allow to see the degree of importance of alternatives in the selected array of purposes.
Keywords: сhoosing a set of alternatives, multicriteria optimization, expert evaluation, classification alternatives.
Введение
В задачах принятия решений в условиях многокритериальности актуальным является вопрос классификации этих критерий. В данной работе рассматривается методика классификации и оптимизации многоцелевых альтернатив, разработанная профессором Юдицким Семеном Абрамовичом. Рассмотрим эту методику на примере производства неконцентрированной азотной кислоты.
Заранее было выбрано множество целей производства. В данном примере рассматриваем два направления развития для улучшения качества производства. Первое направление это повышение надежности. Под надежностью подразумеваем, способность системы сохранять во времени свои основные задачи, такие как смешение NH3 и воздуха, фильтрация и сжатие воздуха, окисление аммиака и т.д. Второе направление это уменьшение финансовых затрат, т.е. нужно найти баланс между финасовыми затратами и повышением надежности системы. Полный список целей для рассматриваемого метода представлен в таблице 1.
Методика заключается в распределение на классы множества альтернатив А = {аi}, i=1,…, B, где ai – значение набора целей (e1...eN*); В = (N*)k, k - число уровней цели.[1, C. 27]
Множество альтернатив А распределяются на классы L1,…, LR исходя из временных ограничений V и на имеющиеся ресурсы Ф.
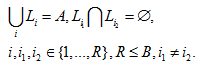 (1)
(1)
В данном примере k=3, где 1– это низкий уровень, 2–это средний и 3–это высокий уровень достижения цели.
Таблица 1 – Список целей предложенных экспертом для рассмотрения
| Обозначение | Содержание |
| E0 | Производство неконцентрированной азотной кислоты |
| E 1 | Надежность ХТС |
| E 1.1 | Уменьшить среднее время восстановления после отказа |
| E 1.2 | Уменьшить интенсивность отказов |
| E 1.3 | Резервирование элементов |
| E 1.4 | Разработка и внедрение способов прогнозирования неисправностей |
| E 1.5 | Применение высоконадежных элементов и оптимизация режимов их работы |
| E 1.6 | Упрощение системы |
| E 2 | Стоимость продукции |
| E 2.1 | Снизить транспортные расходы |
| E 2.2 | Внедрить новые технологии |
Исходя из таблицы видно два класса решений:
![]()
где Ф0, V0 – варьируемые пороговые значения капиталовложений и временем на выполнения.
При минимизации числа локальных альтернатив выяснили, что оптимальный вариант это множество Е = {e1 е2, е3, е4, e5}.[7, С. 38]
e1 – уменьшить среднее время восстановления после отказа;
е2 – уменьшить интенсивность отказов;
е3 – разработка и внедрение способов прогнозирования неисправностей;
е4 – упрощение системы;
e5 – внедрить новые технологии;
Итоговая таблица минимизации числа локальных целей представлена ниже.[7, С. 37-38]
Таблица 2 – Итоговый расчет минимизации локальных целей
| E j | E 1.1 | E 1.2 | E 1.3 | E 1.4 | E 1.5 | E 1.6 | E 2.1 | E 2.2 |
| J(Cj) | 0,145 | 0,207 | -0,07 | 0,195 | 0,109 | 0,163 | 0,104 | 0,149 |
| ej | e1 | e2 | – | e3 | – | e4 | – | e5 |
Классификация
Произведем сортировку альтернатив по классам L1 и L2. Если массив, который будет иметь значение: например A= 11111, то это будет считаться как «худшая» альтернатива и будет удовлетворять введенным ограничениям на ресурсы, т.е. принадлежит классу L1, а «лучшая» альтернатива А= 33333 будет относиться к классу L2 и отвечать «ресурсным возможностям» (здесь и далее альтернативы обозначены 5-значными кодами).
На основе бинарных отношений, которым классифицируется множество А, определяется следующим образом: альтернатива ![]() доминирует над альтернативой
доминирует над альтернативой ![]() , если для любого g = 1,...,N* имеет место
, если для любого g = 1,...,N* имеет место ![]() и существует по меньшей мере одно h = 1 ,..., N* такое, что
и существует по меньшей мере одно h = 1 ,..., N* такое, что ![]() . [1, C. 27]
. [1, C. 27]
Классификация альтернатив осуществляется по алгоритму Ларичева. [1, C. 28]
В первом пункте вычисляются число доминантных альтернатив для каждого ![]() варианта сравнения. Где
варианта сравнения. Где ![]() - число альтернатив,
- число альтернатив, ![]() - число альтернатив, над которыми доминирует
- число альтернатив, над которыми доминирует ![]() .
.
Затем из множества выбираются те альтернативы, для которых ![]()
Из полученных результатов отфильтровываем максимальные значения.
Если еще остались несколько альтернатив, то выбираем любую альтернативу ![]() .
.
Предъявляем ее эксперту, который относит ![]() к одному из классов и после ее классификации экспертом исключаем
к одному из классов и после ее классификации экспертом исключаем ![]() из множества А.
из множества А.
Если ![]() отнесена к классу L1, то из множества А исключаем также все альтернативы, которые доминируются альтернативой
отнесена к классу L1, то из множества А исключаем также все альтернативы, которые доминируются альтернативой ![]() , соответствуют классу L 1.
, соответствуют классу L 1.
Если ![]() отнесена к классу L2, то из множества А исключаем все альтернативы, доминирующие по отношению к
отнесена к классу L2, то из множества А исключаем все альтернативы, доминирующие по отношению к ![]() , соответствуют классу L 2.
, соответствуют классу L 2.
Если ![]() , то возвращаемся к первому пункту, если
, то возвращаемся к первому пункту, если ![]() , то заканчиваем классификацию.[1, C. 28]
, то заканчиваем классификацию.[1, C. 28]
Определение в классе доминантных альтернатив проводим на основе квадратной таблицы, строки и столбцы которой соответствуют альтернативам, принадлежащим выбранному классу.
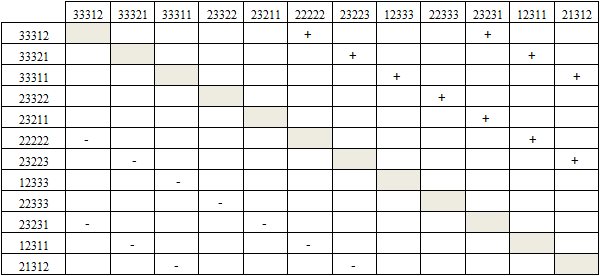
Примером итоговой данного метода служит таблица 3. Таблица рассматривается построчно и в пустые ячейки ставится знак «+» если ![]() , соответственно, если альтернатива аi преобладает над альтернативой аj. Так же если аj не доминирует над аi и в клетку (аj ,аi) ставится знак «-». Незаполненной считается клетка, если в ней нет ни одного знака. Знака «-» упрощает работу и время на рассмотрения пар альтернатив.[1, C. 29]
, соответственно, если альтернатива аi преобладает над альтернативой аj. Так же если аj не доминирует над аi и в клетку (аj ,аi) ставится знак «-». Незаполненной считается клетка, если в ней нет ни одного знака. Знака «-» упрощает работу и время на рассмотрения пар альтернатив.[1, C. 29]
Если в столбце нет знака «+», то такие альтернативы являются доминантными. Согласно таблице 3 это подмножество альтернатив А* = {33312,33321,33311,23322,23211}.
Таблица 3 – Пример работы рассматриваемого алгоритма
Оптимизация
В выбранном классе L1 для каждой доминантной альтернативы ![]() , полученной на предыдущем этапе, вычисляем интегральный показатель
, полученной на предыдущем этапе, вычисляем интегральный показатель ![]() по формуле (2).[1, C. 30]
по формуле (2).[1, C. 30]
![]() (2)
(2)
Для каждой локальной цели ei, i = 1,…,n сопоставляем экспертную функцию принадлежности ![]() , значение этой функции трактуется как задаваемая экспертом вероятность достижения локальной цели. Отображающую уровни eij достижимости цели, выраженные «качественными» значениями, в числа из интервала [0, 1]. Графики функций
, значение этой функции трактуется как задаваемая экспертом вероятность достижения локальной цели. Отображающую уровни eij достижимости цели, выраженные «качественными» значениями, в числа из интервала [0, 1]. Графики функций ![]() для рассматриваемого примера даны ниже.
для рассматриваемого примера даны ниже.
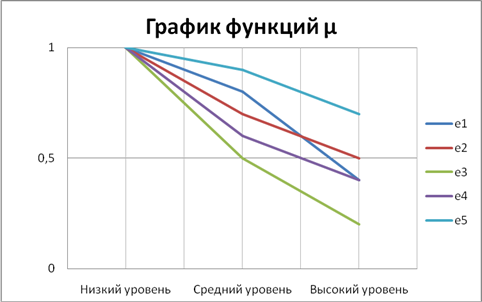
Рис. 1 – График функций ![]() .
.
Далее для каждой доминантной альтернативы, входящей в множество А*, рассчитывается показатель G, равный сумме произведений весов целей ei, i =1,...,5 на соответствующие значения функций принадлежности µ. Результаты даны в таблице 4.
Таблица 4 – Расчет показателя G
| Альтернатива | Расчет G | Значение G |
| 33312 | 0,05·0,4+0,08·0,5+0,25·0,2+0,25+0,06·0,9 | 0,4098 |
| 33321 | 0,05·0,4+0,08·0,5+0,25·0,2+0,25·0,6+0,06 | 0,3174 |
| 33311 | 0,05·0,4+0,08·0,5+0,25·0,2+0,25+0,06 | 0,4158 |
| 23322 | 0,05·0,8+0,08·0,5+0,25·0,2+0,25·0,6+0,06·0,9 | 0,331 |
| 23211 | 0,05·0,8+0,08·0,5+0,25·0,5+0,25+0,06 | 0,5092 |
Заключение
В нашем примере выбираем альтернативу 23211, которая предусматривает максимальное значение 0,51 для показателя G. Эта альтернатива предусматривает:
- средний уровень уменьшения среднее время восстановления после отказа;
- высокий уровень уменьшения интенсивность отказов;
- средний уровень разработки и внедрения способов прогнозирования неисправностей;
- низкий уровень упрощение системы;
- низкий уровень внедрить новые технологии;
Таким образом, данная методика классификации и оптимизации многоцелевых альтернатив позволяет выделить приоритет развития предприятия. В данном примере экспертная оценка не проводилась, необходимо было показать методику. Но уже можно сказать, что данная методика позволит решить поставленную задачу с нахождением баланса между экономией на производство и общим повышением надежности системы.
Список литературы / References
- Юдицкий С.А., Владислав П.Н. Основы предпроектного анализа организационных систем: учебное пособие. – М.: Финансы и статистика, 2005. – 144 с.
- Анкудинов Г.И., Анкудинов И.Г., Иванова И.В., Принятие решений в системном проектировании: Учебник. – СПб: Национальный минерально-сырьевой университет «Горный», 2013. – 176 с.
- Ларичев О.Н. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2000. – 296 с.
- Лотов. А.В., Поспелова И.И., Многокритериальные задачи принятия решений: Учебное пособие. – М.: МАКС Пресс, 2008. – 197 с.
- Черноморов Г.А. Теория принятия решений: Учебное пособие. Новочеркасск: Ред. журн. «Изв. вузов. Электромеханика», 2002.– 276 с.
- Двадцатов, Р.В. Анализ метода взвешивания целей на примере производства азотной кислоты на агрегатах укл-7 / Р. В. Двадцатов // Международный научно-исследовательский журнал. – 2016. – № 10 (52).– С. 30–34.
- Двадцатов, Р.В. Минимизация числа локальных целей системы / Р. В. Двадцатов // Международный научно-исследовательский журнал. – 2016. – № 10 (52).– С. 35-38.
Список литературы на английском языке / References in English
- Judickij S.A., Vladislav P.N. Osnovy predproektnogo analiza organizacionnyh system [Basics of pre-analysis of organizational systems]: Textbook. – M.: Finansy i statistika, 2005. – P. 144. [in Russian]
- Ankudinov G.I., Ankudinov I.G., Ivanova I.V., Prinjatie reshenij v sistemnom proektirovanii [Decision-making in the system design]: – SPb: Nacional'nyj mineral'no-syr'evoj universitet «Gornyj», 2013. – P. 176. [in Russian]
- Larichev O.N. Teorija i metody prinjatija reshenij, a takzhe Hronika sobytij v Volshebnyh stranah [Theory and methods of decision-making, as well as the chronicle of events in a magical land]: Textbook. – M.: Logos, 2000. – P. 296. [in Russian]
- A.V., Pospelova I.I., Mnogokriterial'nye zadachi prinjatija reshenij [Multicriteria decision making problems]: Textbook. – M.: MAKS Press, 2008. – P. 197. [in Russian]
- Chernomorov G.A. Teorija prinjatija reshenij [Decision theory]: Textbook. Novocherkassk: Red. zhurn. «Izv. vuzov. Jelektromehanika», 2002.– P. 276. [in Russian]
- Dvadcatov, R.V. Analiz metoda vzveshivanija celej na primere proizvodstva azotnoj kisloty na agregatah ukl-7 [Analysis method for example purposes weighing nitric acid production at ukl-7]/ R. V. Dvadcatov // International Research Journal. – 2016. – № 10 (52).– P. 30–34. [in Russian]
- Dvadcatov, R.V. Minimizacija chisla lokal'nyh celej sistemy / R. V. Dvadcatov [Minimizing the number of local objectives system]// International Research Journal. – 2016. – № 10 (52).– P. 35-38. [in Russian]
