ИССЛЕДОВАНИЕ УДАРА ПО РАВНОМЕРНО РАСТЯНУТОЙ ПЛАСТИНЕ, ЛЕЖАЩЕЙ НА ОСНОВАНИИ

Рухленко С. А.

Доцент, кандидат физико-математических наук,

Донской государственный технический университет (г. Ростов-на-Дону)

ИССЛЕДОВАНИЕ УДАРА ПО РАВНОМЕРНО РАСТЯНУТОЙ ПЛАСТИНЕ, ЛЕЖАЩЕЙ НА ОСНОВАНИИ

Аннотация

Исследуется удар массивного тела по равномерно растянутой (сжатой) пластине, лежащей на основании. Общие перемещения пластины считаются упругими, а местные в области контакта – упругопластическими. Рассматривается единый подход при анализе удара по центру прямоугольной или круглой пластины, лежащей на основании Винклера или по бесконечной пластине на поверхности идеальной несжимаемой жидкости. При расчете основных характеристик удара (силы контактного взаимодействия, её максимума, момента его достижения, продолжительности соударения, коэффициента восстановления при ударе) важным является учёт начальной скорости соударения, величины внешних воздействий на тело и пластину, состояния материалов тел. Проведён анализ динамической функции влияния системы «пластина – основание». Соударение рассматрива­ется в рамках теории С. П. Тимошенко, в которой пренебрегают волновыми процессами в малой области контакта тел. В работе используется решение квазистатической контактной задачи для упругопластических тел, хорошо согласующееся с численными и эмпирическими результатами. При больших местных пластических деформациях можно пренебречь упругостью материала в области контакта, использовать решение жесткопластической контактной задачи и исследовать жёсткопластическое соударение. Полученные асимптотические результаты хорошо согласуются с аналитическими и численными решениями задачи удара по полупространству и по бесконечной пластине и могут быть рекомендованы для инженерных расчетов.

Ключевые слова: упругопластическое соударение, прямоугольная, круглая, бесконечная пластины, равномерное растяжение, основание, асимптотика.

Rukhlenko S.A.

PhD in Physics and Mathematics, associate professor,

Don state technical university (Rostov-on-Don)

STUDY OF THE BLOW EVENLY STRETCHED PLATE LYING ON THE BASE

Abstract

Examines the impact of a massive body at evenly stretched (compressed) plate, lying on the ground. The total displacement of the plate is considered elastic, and local to the contact is elastic-plastic. Considered a common approach in the analysis of the attack on the center of a rectangular or circular plate lying on the base of the Winkler or an endless plate on the surface of an ideal incompressible fluid. When calculating the main characteristics of the impact (force of contact interaction, its maximum, the moment of achievement, duration of impact, coefficient of restitution at impact) important is the consideration of the initial impact velocity, the magnitude of the external influences on the body and the plate, the state of material bodies. the analysis of the dynamic function of the influence of the «plate – base». The collision is considered in the framework of the theory of S. P. Timoshenko, which neglect wave processes in a small area of contact. The solution of the quasistatic contact problems for elastoplastic bodies, which are in good agreement with numerical and empirical results. For large local plastic deformations can be neglected elasticity of the material in the contact area, use the solution to rigid-plastic contact problem and to investigate rigid-plastic collision. The asymptotic results are in good agreement with analytical and numerical solutions to the problem of hitting the half-space and an endless plate and can be recommended for engineering calculations.

Keywords: elastoplastic collision, rectangular, circular, endless plate, even stretching, base, asymptotics.

Определяются характеристики соударения твердых деформируемых тел: сила контактного взаимодействия, время контакта, проникание. Используется модель местного смятия α(P) для упругопластических тел [1].

В [2], [4], [6], [7] рассмотрено влияние на параметры удара равномерных растягивающих усилий в плоскости пластины. В [3] исследовался удар массивного тела по пластине на упругом жидком полупространстве, а в [5] – по круглой пластине со свободным краем, лежащей на основании Винклера.

Удар по прямоугольной шарнирно опёртой пластине. В рамках постановки задачи [6], [7] исследуется удар тела массы m, двигающегося со скоростью V₀, по центру шарнирно опёртой прямоугольной пластины толщины h, равномерно растянутой (сжатой) в своей плоскости усилиями p₀ и лежащей на основании Винклера с коэффициентом постели k₀. Радиус кривизны тела в точке удара равен R. Согласно теории удара С.П.Тимошенко перемещение z(t) тела равно сумме местного смятия  и перемещения w пластины в точке удара:

,                                      (1)

где a, b – стороны пластины, . Уравнение движения тела под действием сил тяжести и контактного взаимодействия P(t) запишем в виде:

                                     (2)

где g – ускорение свободного падения. Решение контактной задачи [1] представляется в виде:

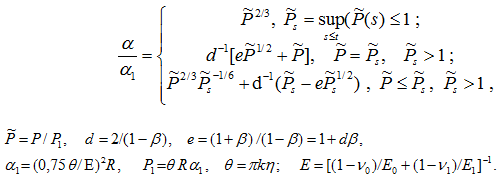                           (3)

Здесь Р₁ и  – контактная сила и местное смятие, при которых начинают учитываться пластические деформации;  – модули Юнга и коэффициенты Пуассона тела и пластины;  – наименьшая пластическая константа одного из тел, в котором происходят пластические деформации;  при отсутствии трения между телами, при этом для квадратичного зазора  характеризует пластическое вытекание материала из-под штампа.  – цилиндрическая жёсткость пластины,  – интенсивность растягивающей нагрузки.

Перемещение пластины представим в виде:

                                 (4)

где динамическая функция влияния (ФВ) Грина f(х, у, t) описывает перемещение пластины в результате воздействия на её центр сосредоточенного единичного импульса .

Асимптотическое поведение нормированной ФВ (НФВ)

,                                  (5)

в точке удара (в центре пластины) исследовалось в [6] и [7] при больших и малых значениях безразмерного времени , а также при больших и малых значениях параметра , где 

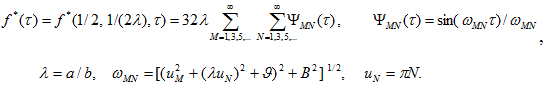    (6)

При малых 

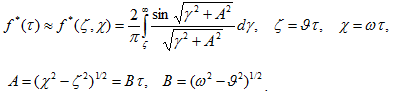               (7)

 является НФВ для равномерно растянутой бесконечной пластины (БП) на основании Винклера. При   является решением Лурье  для БП на винклеровском основании. Т.к.  не зависят от размеров a и b пластины, то из (7) следует, что при малых  край пластины не влияет на ее смещение в точке удара.

Получено эффективное асимптотическое решение для ФВ, соответствующее большим значениям :

                     (8)

При больших значениях параметра B

Произведём замену переменных

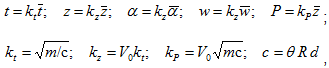
где коэффициенты  отношения размерных параметров удара к безразмерным представляют собой их максимальные значения при жесткопластическом ударе (ЖПУ) тела по полупространству без учёта силы тяжести [2]. Опуская надчерки, получаем безразмерную систему уравнений:

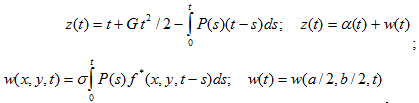                             (9)

где  – нормированная ФВ;

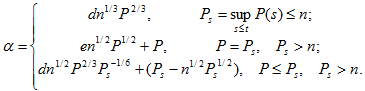
При малых n используем решение жёсткопластической контактной задачи

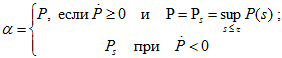
и решение задачи ЖПУ. Обозначим через X, Z, W, F* преобразования Лапласа с параметром s по безразмерному времени t функций P, z, w и  f*. На этапе нагружения при ЖПУ

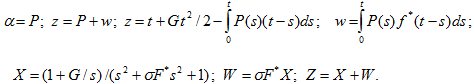                  (10)

Из (10) при  определяется решение ЖПУ по полупространству:

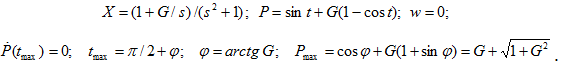
При больших G значение P_max эквивалентно 2G. Решение при G=0 ниже обозначается верхним индексом «0» и имеет вид:

                    (11)

Рассматриваемое решение для безразмерной силы удара имеет вид половины волны синусоиды с соответствующим эффектом моментальной разгрузки, т.е. для момента  завершения удара .

При нагружении  находим решение ЖПУ по бесконечной свободной пластине:

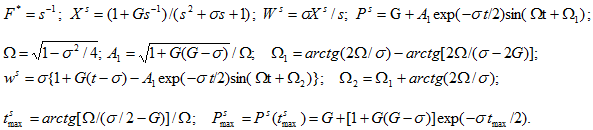                     (12)

При G=0 и малых , выделяя (11) в (12), можно получить приближённое решение

Подстановка  в уравнение  позволяет определить  и приближённые параметры удара:

            (13)

Согласно принятым обозначениям (t безразмерное)

С учётом свойств дельта-функции Дирака, из (8) следует:

    (14)

При больших , т.е. при больших B, получим .

В принятых обозначениях НФВ для БП на винклеровском основании:

При исследовании ЖПУ массивного тела по БП на винклеровском основании  исследована зависимость наибольшей силы удара Р_max и момента её достижения t_max от параметров  и l, характеризующих податливость БП и жёсткость основания Винклера: БП в случае l=0 считается свободной, а при больших l параметры удара приближаются к соответствующим значениям удара по полупространству . При исследовании ЖПУ по квадратной пластине следует использовать два подхода. Если сторона пластины a неограниченно возрастает, то  стремится к бесконечности, а произведение , не зависящее от a, остаётся конечным. При больших  система (3) исследуется относительно параметров .

При k₀=0 винклеровское основание отсутствует , а отношение , не зависящее от коэффициента k₀, выступает в качестве параметра, характеризующего размер пластины. Поэтому при малых  следует рассматривать зависимость системы (3) от параметра , представляющего влияние размера пластины на процесс удара. При этом система (3) исследуется относительно параметров . Параметр  представляет влияние размера пластины на процесс удара.

Используя (14), строим приближённые решения ЖПУ в случае, когда смещение пластины в процессе удара мало, а параметры удара близки к соответствующим значениям параметров ЖПУ по полупространству. При больших значениях параметра B, подставив (14) в (10), находим

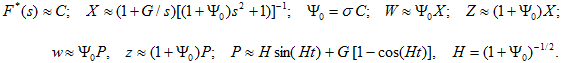   (15)

В момент времени t_max достижения максимума силы контакта , откуда в результате преобразований определяются параметры удара

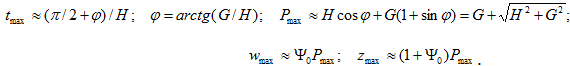   (16)

При G=0

причем для малых 

                (17)

Подставляя (17) и (13) в неравенство , которое подтверждается результатами численного анализа, получим, что (16 и (17) имеют смысл и являются эффективными лишь при  в случае малых значений параметра B, эти решения следует также использовать при  в случае больших значений B.

На этапе разгрузки при ЖПУ система уравнений движения при любых G может быть записана с учётом (14) в приближённом виде

     (18)

Решая (18) относительно Р(t), находим

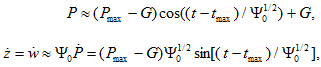                                  (19)

откуда определяются приближённые значения параметров удара в момент  завершения контакта:

                  (20)

где t_max и Р_max имеют вид (16). Величина  равна коэффициенту восстановления скорости при ЖПУ. Из (20) следует, что при ЖПУ скорость отскока массивного тела может быть значительной в результате передачи ему упругой энергии пластины и основания.

При больших B, т.е. при больших , пластину можно считать бесконечной, а край пластины начинает оказывать влияние на процесс удара, если  заметно отличается от . При малых  жёсткость основания мала и влияет на процесс удара, если  заметно отличается от .

Нормальный удар по бесконечной пластине, лежащей на поверхности идеальной несжимаемой жидкости. НФВ построена в работе [2], где приведена таблица значений функции  для  Построена асимптотика  при малых и больших значениях параметра , характеризующего инерционные свойства жидкости и зависящего от безразмерного времени.

При малых значениях  получена зависимость

 .                         (21)

Асимптотика функции при больших  имеет следующий вид:

                    (22)

Путём замены  на  получаем приближённую формулу, применимую при любом :

                                      (23).

Численный анализ показывает, что абсолютная погрешность вычисления по формуле (23) не выше 0.017 и как функция аргумента  близка к функции плотности нормального распределения, умноженной на некоторое число. Применяя метод наименьших квадратов, получим параметры этого распределения и приближённую зависимость для вычисления НФВ:

                (24)

Абсолютная погрешность вычисления по формуле (24) не превосходит 0.0007 .

При решении системы уравнений движения функция  определялась путём интерполяции табличных значений и использования построенных асимптотик (21) и (22). Однако, высокая точность вычисления по приближённой формуле (24) допускает её применение в расчётах вместо указанной процедуры вычисления функции влияния. В [2] приведены графики зависимости безразмерных характеристик ЖПУ удара  от параметра  для различных значений параметра j, характеризующего инерционность жидкого основания.

Удар по центру круглой пластины со свободным краем, лежащей на винклеровском основании. Пусть сосредоточенный импульс прикладывается в центре пластины, лежащей на винклеровском основании и ограниченной контуром r=L. НФВ исследуется относительно безразмерного времени  и параметра :

               (25)

В [5] показано, что приближённые значения коэффициентов (25) можно определить по приближённым формулам .

Первое слагаемое в (25) соответствует движению пластины как массивного тела массы , закреплённого на пружине жёсткости . Для свободной пластины , то есть . При больших  из (25) получена приближённая формула

                                      (26)

Если в (26) пренебречь первым слагаемым, то есть общими перемещениями пластины как массивного тела, и учитывать равномерное растяжение (сжатие), то для круглой пластины так же, как и для прямоугольной пластины, при определённы условиях можно использовать приближённое решение (8) для НФВ и асимптотические решения ЖПУ (15) – (19).

Список литературы / References

1. Александров В.М., Кадомцев И.Г., Царюк Л.Б. Осесимметричные контактные задачи для упругопластических тел // Трение и износ. – 1984. – Т.5. – №1. – С. 16-26.
2. Кадомцев И. Г., Рухленко С. А. Удар массивного тела по бесконечной пластине, лежащей на жидком полупространстве, с учётом контактных явлений / И. Г.Кадомцев, С. А. Рухленко // Изв. СКНЦ ВШ. Естеств. науки. – 1989. – № 3. – С. 22-29.
3. Рухленко С.А. Упругопластический удар по бесконечной пластине, лежащей на упругом жидком полупространстве // Численные и аналитические методы решения задач строительной механики и теории упругости. – Ростов н/Д: Рост. инж.-строит. ин-т, 1989. – С. 65-74.
4. Рухленко С.А. Поперечный удар массивного тела по равномерно растянутой бесконечной пластине с учётом упругопластического контактного взаимодействия // Численные методы решения задач теории упругости и пластичности. Материалы XI Всесоюзной конференции, г. Волгоград, 10-12 октября 1989 г. – Новосибирск, 1990. – С. 186-190.
5. Кадомцев И.Г. Упругопластический удар массивного тела по круглой пластине, лежащей на винклеровском основании / И. Г. Кадомцев, С. А. Рухленко // Фундаментальные и прикладные проблемы механики деформируемых сред и конструкций. Программа Государственного Комитета РФ по высшему образованию. Научные труды. Выпуск 1. – Н.Новгород: Из-во Нижегородского ун-та, 1993. – С. 104-111.
6. Кадомцев И. Г. Упругопластический удар массивного тела по прямоугольной пластине / И. Г. Кадомцев, Г. К. Барановский, С. А. Рухленко // Изв. вузов. Северо-Кавказский регион. Естеств. науки. – 2000. – № 3. – С. 68-71.
7. Рухленко С.А. Удар тела по равномерно растянутой прямоугольной пластине на основании / С. А. Рухленко // Научное обозрение. – 2015. – № 24. – С. 92-97.

Список литературы на английском языке / References in English

1. Aleksandrov V. M. Osesimmetrichnye kontaktnye zadachi dlja uprugoplasticheskih tel [Axisymmetric contact problems for elastoplastic bodies] / V. M. Aleksandrov, I. G. Kadomcev, L. B. Carjuk // Trenie i iznos [Friction and wear]. – 1984. – T.5. – №1. – P. 16-26. [in Russian]
2. Kadomcev I.G. Udar massivnogo tela po beskonechnoj plastine, lezhashhej na zhidkom poluprostranstve, s uchjotom kontaktnyh javlenij [Iimpact of a massive body on an endless plate lying on a liquid semispace, with the consideration of contact phenomena] / I. G. Kadomcev, S. A. Ruhlenko // Izv. SKNTs VSh. Estestv. nauki. – 1989. – № 3. – P. 22-29. [in Russian]
3. Ruhlenko S. A. Uprugoplasticheskiy udar po beskonechnoy plastine, lezhashhey na uprugom zhidkom poluprostranstve [Elastoplastic impact on an endless plate lying on an elastic liquid half-space] / S. A. Ruhlenko // Chislennye i analiticheskie metody reshenija zadach stroitel'noy mehaniki i teorii uprugosti [Numerical and analytical methods for solving problems of structural mechanics and theory of elasticity]. – Rostov-on-Don: Rost. inzh.-stroit. in-t, 1989. – P. 65-74. [in Russian]
4. Ruhlenko S.A. Poperechnyy udar massivnogo tela po ravnomerno rastjanutoy beskonechnoy plastine s uchjotom uprugoplasticheskogo kontaktnogo vzaimodejstvija [Transverse impact of a massive body on an evenly stretched endless plate with the consideration of elastoplastic contact interaction] / S. A. Ruhlenko // Chislennye metody reshenija zadach teorii uprugosti i plastichnosti. Mat-ly XI Vsesojuz. konf., g. Volgograd, 10-12 okt. 1989 g. [Numerical methods of solving problems of elasticity and plasticity theory. Proceedings of the XI All-Union conf., Volgograd, 10-12 October 1989.] – Novosibirsk, 1990. – P. 186-190. [in Russian]
5. Kadomcev I. G. Uprugoplasticheskiy udar massivnogo tela po krugloy plastine, lezhashhey na vinklerovskom osnovanii [Elastoplastic impact of a massive body on a circular plate lying on the base winklervosses] / I. G. Kadomcev, S. A. Ruhlenko // Fundamental'nye i prikl. problemy mehaniki deform. sred i konstrukciy. Programma Gos. Komiteta RF po vysshemu obrazovaniju. Nauchnye trudy. Vyp. 1. [Fundamental and applied problems of mechanics of deformable continua and structures. The program of the RF State Committee for higher education. The scientific works. Issue 1]. – N.Novgorod: Iz-vo Nizhegorodskogo un-ta, 1993. – P. 104-111. [in Russian]
6. Kadomcev I. G. Uprugoplasticheskij udar massivnogo tela po prjamougol'noj plastine [Elastoplastic impact of a massive body on a rectangular plate] / I. G. Kadomcev, G. K. Baranovsky, S. A. Ruhlenko // Izv. vuzov. Severo-Kavkazskiy region. Estestv. nauki [News of higher education institutions. North Caucasus region. Natural sciences]. – 2000. – № 3. – P. 68-71. [in Russian]
7. Ruhlenko S. A. Udar tela po ravnomerno rastjanutoj prjamougol'noj plastine na osnovanii [Impact of a body on an evenly stretched rectangular plate on a base] / S. A. Ruhlenko // Nauchnoe obozrenie [Scientific review]. – 2015. – № 24. – P. 92-97. [in Russian]