ИССЛЕДОВАНИЕ ПРОЦЕССОВ СРЕЗАНИЯ ПРИПУСКОВ ЗЕНКЕРАМИ С МНП ПРИ ОБРАБОТКЕ ТВЕРДЫХ МАТЕРИАЛОВ

Дерябин И. П.¹, Токарев А. С.²

¹Доктор технических наук, Южно-Уральский государственный Университет, ²ORCID: 0000-0003-3902-5785, Аспирант, Южно-Уральский государственный Университет,  старший преподаватель, Трехгорный технологический институт - филиал «Национального исследовательского ядерного университета «МИФИ»

ИССЛЕДОВАНИЕ ПРОЦЕССОВ СРЕЗАНИЯ ПРИПУСКОВ ЗЕНКЕРАМИ С МНП ПРИ ОБРАБОТКЕ ТВЕРДЫХ МАТЕРИАЛОВ

Аннотация

В статье исследуется процесс формообразования срезаемых сечений припуска трех лезвийным зенкером с многогранными неперетачиваемыми пластинами, при обработке твердых материалов. Разработана масштабная и математическая модель для расчета площадей срезаемых сечений. Для построения масштабной модели использовалась программа KOMPAS-3D V16, которая позволила измерить площади сечений срезаемые каждым лезвием. Сравнение моделей показало адекватность применения данного метода при обработке точных и глубоких отверстий.

Ключевые слова: Зенкер с МНП, обработка точных и глубоких отверстий, увод оси, математическая модель.

Deryabin I. P.¹, Tokarev A. S.²

¹PhD in Engineering, South Ural state University, ²ORCID: 0000-0003-3902-5785, Postgraduate student, South Ural state University, senior lecturer, Trekhgorny technological Institute branch of "National research nuclear University "MEPhI"

STUDY OF THE PROCESSES OF CUTTING ALLOWANCES BY COUNTERBORING, WITH MNES IN THE PROCESSING OF SOLID MATERIALS

Abstract

This article examines the process of forming cut sections of the stock three bladed countersink with a multifaceted profile inserts, when machining hard materials. Developed large-scale and mathematical model for calculation of areas cut away sections. To build a scale model we used the program KOMPAS-3D V16, which allowed to measure area of cross sections cut away each blade. Comparison of models showed the adequacy of this technique in processing accurate and deep holes.

Keywords: Zenker with MNP, processing accurate and deep holes, pull the axis mathematical model.

Для обработки цилиндрических и конических поверхностей часто используется такой метод обработки как зенкерование. Зенкер- это специальный режущий инструмент, для обработки отверстий. Этот инструмент, позволяет увеличить точность обработки и значительно повысить качество обрабатываемой поверхности. [1, C. 45]

 Зенкерование обычно является получистовой обработкой резанием. Исходя из полученных сведений, можно сделать следующие основные назначения зенкерования:

• Очистка и сглаживание поверхности отверстий: перед нарезанием резьбы или развёртыванием;
• Калибрование отверстий: для болтов, шпилек и другого крепежа.

Зенкерование выполняется после сверления или в литьевых отверстиях.

Процесс зенкерования можно отнести к точным механическим операциям. Такие операции требуют высокой мощности, и выполняются на следующих станках:

Сверлильные станки всех типов: наиболее часто. Станки токарной группы: наиболее часто. Расточные станки: часто как вторичная операция. Фрезерные (горизонтальные и вертикальные): редко. В основном на фрезерных с ЧПУ (как часть программы). Агрегатные станки: как одна из операций в автоматической линии. [2, С . 78]

Инструментом зенкерования является зенкер. Он представляет из себя многолезвийный инструмент, в среднем насчитывается от трех до двенадцати лезвий. Зенкер имеет ось вращения, а обработка ведется кромками режущих лезвий.

Диаметр зенкера всегда принимают меньше окончательного отверстия, так как окончательной операцией является обработка развертыванием. Очень редко зенкерование является окончательной операцией, в основном зенкер используют для промежуточной операции. [3, С. 89]

Основными материалами для изготовления зенкеров являются быстрорежущие стали. Встречаются конструкции этого инструмента, когда на режущих кромках крепятся специальные пластины из твердого сплава. При зенкеровании широко применяются смазочно-охлаждающие вещества.

Зенкера с многогранными неперетачиваемыми пластинами (МНП), в последнее время становятся все более популярными Рассмотрим конструкцию зенкера на рисунке 1.

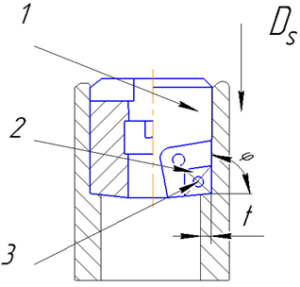
Рис. 1 – Конструкция зенкера с МНП

 

При обработке отверстий зенкерами исследуется схема формообразования отверстий. Режущая пластинка 2 закрепляется в корпусе зенкера  1.  Где: φ – главный угол в плане; t - подача; Ds - направление движение инструмента.

Различные схемы получаются из-за различных конструкций данного лезвийного инструмента, которые представлены на рисунках 2–3.

На рисунке 2 представлена схема формообразования зенкеров оснащенных МНП, без разделения срезаемого слоя, где: t – припуск; Ds – направление подачи; Dmax – максимальный диаметр обработанного отверстия; Dисх – исходный диаметр отверстия

 

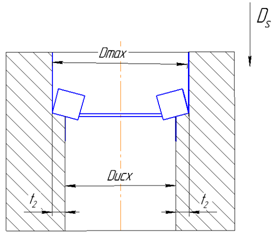
Рис. 2 – Схема формообразования зенкеров оснащенных МНП,без разделения срезаемого слоя

 

На рисунке 3 представлена схема формообразования зенкеров оснащенных МНП, с разделением срезаемого слоя, где:

t1 и t2 – припуск 1 и 2 лезвия соответственно; Dmax – максимальный диаметр обработанного отверстия; Dисх – исходный диаметр отверстия.

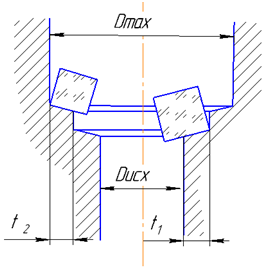
Рис. 3– Схема формообразования зенкеров оснащенных МНП, с разделением срезаемого слоя

 

Такие схемы формообразования не дают полного представления об обработке отверстий. Для получения фактических сечений срезаемых слоев припуска и расчета их площадей необходимо учитывать погрешности расположения пластин в инструменте.

Рассмотрим случай формообразования отверстия зенкером с МНП, когда погрешность расположения пластин τ, будет больше подачи на зуб, (рис. 4), такое возникает при обработке отверстий с малыми подачами, когда обрабатываются твердые материалы: стали и чугуны. Для этого в среде Компас 3D V16 построим схему формообразования и масштабную модель площадей срезаемых слоев. На схеме условно изображены три лезвия исследуемого инструмента, показаны вершины радиус-векторов ρ1(ψ), ρ2(ψ+120⁰), ρ3(ψ+240⁰), ρ1(ψ+360⁰), ψ - угол поворота зенкера с МНП;  подача на оборот S, и главные углы в плане, φ1=88⁰, φ2=90⁰, φ3=92⁰, также показана погрешность расположения пластин τ.

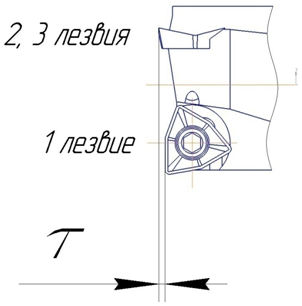
Рис. 4 - погрешность расположения пластин

  Схема формообразования показана на рисунке 5: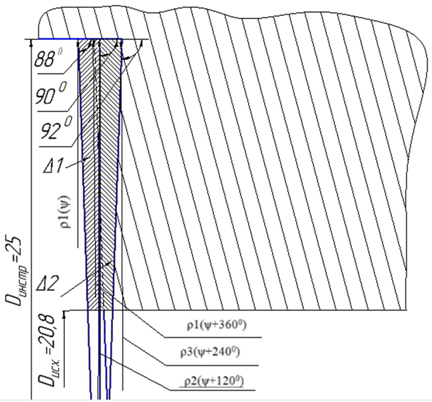  

Рис. 5 – Схема формообразования

 

Зададим необходимые параметры. Диаметр исследуемого зенкера 25 мм. Диаметр предварительного отверстия 20,8 мм. Погрешность расположения пластин 0,2 мм. Подача инструмента 0,15 мм/об. Погрешность главных углов в плане ±2 градуса, в нашем случае φ1=88⁰, φ2=90⁰, φ3=92⁰.

Для нахождения площади срезаемой первым лезвием рассмотрим подробно схему формообразования.

На рисунке 6 показана площадь сечения припуска срезаемая первым лезвием.

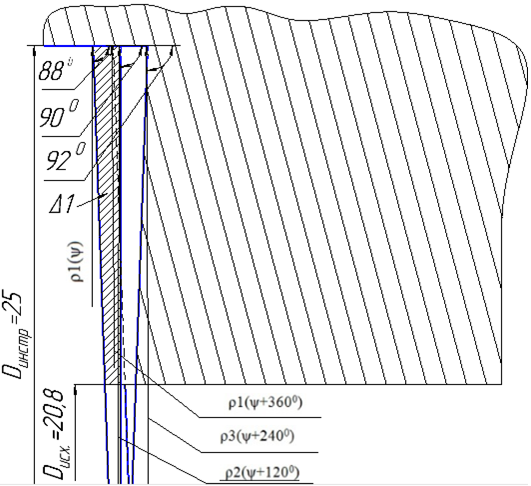
Рис. 6 – Площадь сечения припуска срезаемая первым лезвием

Из рисунка 6 видно, что участок срезаемый первым лезвием это прямоугольная трапеция. Поэтому площадь этого участка будем искать как площадь трапеции по формуле 1.

  (1) где h – (АК) – высота трапеции АВСD; ВС и AD – основания трапеции. Найдем высоту трапеции по формуле 2:

   (2)

где ρ1(ψ) – координаты радиус-вектора вершины первого лезвия;

dисх – диаметр предварительного отверстия.

Найдем длину верхнего основания трапеции, по формуле 3:

  (3)

где S – подача инструмента; τ – погрешность расположения пластин. Найдем длину нижнего основания трапеции, по формуле 4:   (4)

Подставляя полученные выражения в уравнение 5 найдем площадь сечения припуска срезаемую первым лезвием:

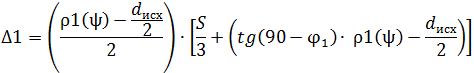  (5)

На рисунке 7 показана площадь сечения припуска срезаемая вторым лезвием.

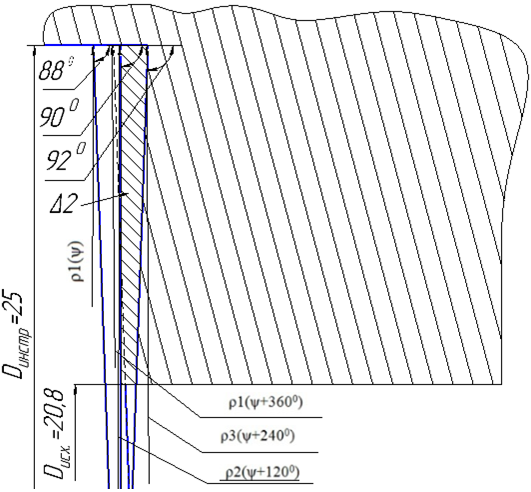
Рис. 7 – Площадь сечения припуска срезаемая вторым лезвием

Из рисунка видно, что участок срезаемый вторым лезвием, также как и в первом случае это прямоугольная трапеция.

Площадь, срезаемую вторым лезвием, найдем по формуле 1.

Высоту трапеции найдем по формуле 6:

  (6)

где ρ2(ψ+120⁰) – координаты радиус-вектора вершины второго лезвия.

Найдем верхнее основание трапеции по формуле 7:

  (7)

Найдем нижнее основание трапеции по формуле 8:   (8)

Подставляя полученные выражения в формулу 8 найдем площадь, срезаемую вторым лезвием:

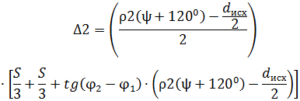  (9)

Когда погрешность расположения пластин τ, будет меньше подачи на зуб, 3 лезвие зенкера не срезает никакого слоя, т.е. является зачистным.

В итоге получившаяся математическая модель расчета площадей срезаемых слоев для первого случая примет вид:

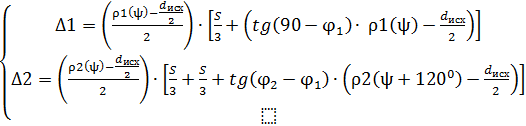  (10)

В построенной модели в среде КОМПАС-3D V16 были количественно измерены площади (рис. 8, 9) и сравнены с расчетными, полученными по математической модели (табл. 1).

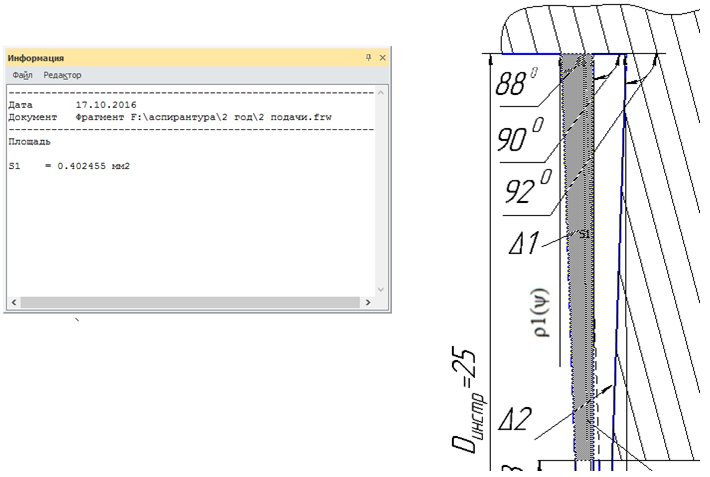
Рис. 8 - Измерение площади сечения припуска срезаемой первым лезвием

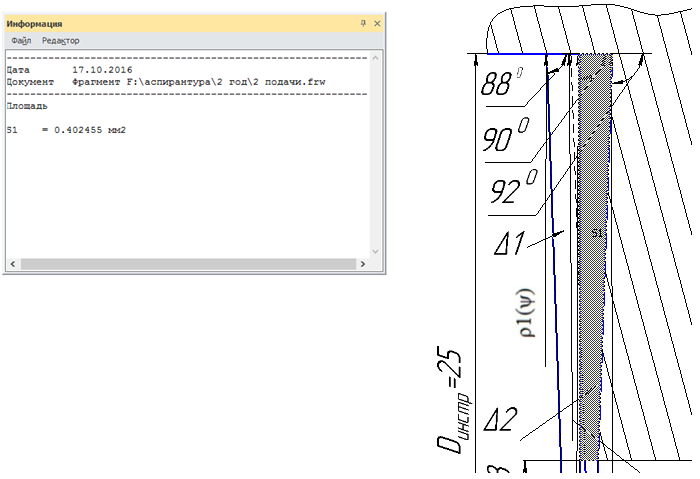
Рис. 9 - Измерение площади сечения припуска срезаемой вторым лезвием

 

Таблица 1 – Проверка адекватности математической модели

Площадь	Измеренная, мм2	Рассчитанная, мм2	Погрешность измерения, %
Δ1	0,402455	≈0,397243	1,3
Δ2	0,402455	≈0,415475	3,2

 

Вывод:

Как видно из таблицы, погрешность измерений и вычислений составляет не более 3,2%, что является допустимым отклонением.

Таким образом, можно сделать вывод, что данная математическая модель адекватна и может применяться при расчетах точности обработки.

Список литературы/ References

1. Драгун А.П. Режущий инструмент / А. П. Драгун. – Л.: Лениздат, 1986. – 271 с.
2. Петрушин С.И. Основы формообразования резанием лезвийными инструментами / С. И. Петрушин . Учебное пособие. Томск: Изд. ТГУ, 2003. – 172с.
3. Пестрецов, С.И. Компьютерное моделирование и оптимизация процессов резания: учеб. пособие / С.И. Пестрецов. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2009 – 104 с. – 100 экз. – ISBN978-5-8265-0795-7.

Список литературы на английском языке/ References in English

1. Dragun A.P. Rezhushhij instrument [Cutting instrument] / A. P. Dragun. – L.: Lenizdat, 1986. – 271 p.
2. Petrushin S.I. Osnovy formoobrazovanija rezaniem lezvijnymi instrumentami [Fundamentals of forming cutting blade tools] / S. I. Petrushin . Textbook. Tomsk: Izd. TGU, 2003. – 172 p.
3. Pestrecov, S.I. Komp'juternoe modelirovanie i optimizacija processov rezanija: ucheb. posobie [Computer simulation and optimization of cutting processes: proc. allowance] / S.I. Pestrecov. – Tambov: Izd-vo Tamb. gos. tehn. un-ta, 2009 – 104 p. – 100 exe. – ISBN978-5-8265-0795-7.