ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ АЛГЕБРЫ ДЛЯ ОПТИМИЗАЦИИ КОЛИЧЕСТВА ПРИБОРОВ В СИСТЕМАХ СВЕДЕНИЯ БАЛАНСА

Кувыкин В.И.¹, Кувыкина Е.В.²

¹ORCID: 0000-0002-5283-0028, Доктор физико-математических наук, ООО «ЛУКОЙЛ-Нижегороднефтеоргсинтез»

²ORCID: 0000-0002-5437-8995, Кандидат физико-математических наук, Доцент, Национальный исследовательский нижегородский государственный университет им. Н.И. Лобачевского

ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ АЛГЕБРЫ ДЛЯ ОПТИМИЗАЦИИ КОЛИЧЕСТВА ПРИБОРОВ В СИСТЕМАХ СВЕДЕНИЯ БАЛАНСА

Аннотация

Рассмотрена задача оптимизации количества измерительных приборов в системе сведения материального баланса. Предложен алгоритм расчета и размещения минимального количества измерителей, обеспечивающий определение расхода для всех материальных потоков. Разработан эвристический алгоритм расположения дополнительных приборов, повышающих надежность измерений. Для решения задач использована система компьютерной алгебры. Описано практическое использование результатов исследования при создании автоматизированной системы сведения материального баланса нефтеперерабатывающего предприятия.

Ключевые слова: моделирование, методы оптимизации, измерительные приборы, компьютерные приложения, материальный баланс.

Kuvykin V. I. ¹, Kuvykina E. V. ²

¹ORCID: 0000-0002-5283-0028, PhD in Physics and Mathematics, OOO «LUKOIL-Nizhegorodnefteorgsintez»

²ORCID: 0000-0002-5437-8995, PhD in Physics and Mathematics, associate professor, National Research Lobachevsky State University of Nizhni Novgorod

COMPUTER ALGEBRA APPLICATION FOR MEASURING INSTRUMENT QUANTITY OPTIMIZATION FOR MATERIAL BALANCE RECONCILIATION

Abstract

The problem of optimization of the number of measuring devices for refinery material balance reconciliation is considered. The algorithm for minimization of measuring devices quantity for data reconciliation and identification all flows is designed. Arrangement redundancy measuring devices algorithm is proposed. Heuristic algorithm for gross error detection is developed. Computer algebra system is used for solving these problems. The practical implementation of the research study results for refinery material balance system design is described.

Keywords: models, optimization methods, measuring instruments, computer applications, material balance.

Сведение материального баланса является необходимым звеном в системах учета и управления технологическими процессами в различных отраслях: переработка сельскохозяйственной продукции [1,2], распределения энергоресурсов, нефтехимическая промышленность [3,4], системы смешения продукции [5]. Требования к современным автоматизированным системам учета в бизнесе по точности и надежности измерений непрерывно возрастают.

Измерения в балансовых  системах, как правило, дублируются, что дает возможность своевременно диагностировать неприемлемые ошибки приборных данных. Дополнительные измерения позволяют повысить надежность и безопасность, улучшить работу систем управления. На промышленных предприятиях насчитываются сотни приборов. Актуальной задачей является определение минимального количества измерительных средств и их оптимальное размещение, что позволяет существенно снизить инвестиционные и эксплуатационные затраты и повысить эффективность производства.

Решить методом проб и ошибок задачу оптимизации количества приборов учета для целей расчета баланса в промышленных системах большой размерности практически невозможно. Существенную помощь при решении сложных прикладных задач могут оказать методы компьютерной алгебры [6,7]. На возможность использования символьных вычислений при согласовании данных указано в работе [8]. В данной статье развиваются подходы с применением систем компьютерной алгебры для организации автоматизированного приборного учета.

Целью работы является разработка алгоритма оптимизации измерительных устройств в системах сведения баланса с использованием компьютерной алгебры: расчет минимального количества измерителей для определения состояния системы; определение расположения дополнительных приборов, обеспечивающих работу при поломке одного из них.

При  составлении материального баланса, помимо уравнений, описывающих закон сохранения массы, используется поточная схема производства [3]. Рассмотрим схему производственных потоков, состоящую из m узлов   и содержащую n потоков с расходом  . Примем для входящих в узел  потоков  знак минус, для выходящих – плюс, для отсутствующих потоков –нулевое значение.

Система уравнений для поточной модели баланса имеет вид [2]:

                                                (1)

где   - вектор решений,  - матрица  коэффициентов, содержащая значения -1, 0, +1.

Для определения расхода достаточно использовать лишь некоторое количество измеряемых потоков. Неизмеряемые потоки принято подразделять на наблюдаемые, значения расхода которых можно вычислить по известным значениям измеренных величин, и ненаблюдаемые [3].

Обозначим подмножество измеряемых потоков , наблюдаемых -  и ненаблюдаемых - , с элементами .

Вычислим минимальное количество k измерительных средств при отсутствии ненаблюдаемых потоков, т.е. множество  - пустое.

Обозначим ранг матрицы . Как следует из решения системы линейных однородных уравнений,  неизвестных могут быть выбраны произвольно и все решения системы могут быть получены построением линейной комбинации из  независимых решений [9]. Таким образом, достаточное для определения всех значений расхода количество приборов .

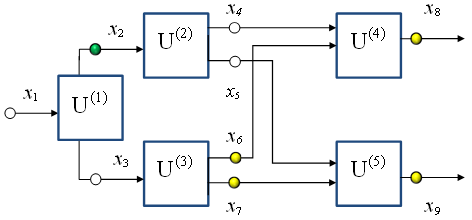
Рис. 1. Схема потоков с расходом с узлами ;  - измеряемые значения,  - дополнительное измеряемое значение, обеспечивающее учет при выходе из строя любого из приборов.

Следует отметить, что решение задачи о размещении приборов в системе учета является неоднозначным, более того, произвольное расположение может привести к ненаблюдаемым потокам. Таким образом, следующим шагом после определения минимального количества приборов является оптимальное расположение приборов.

Решения в символьной форме позволяют ответить на вопрос о размещении средств измерения, если представить расход  для наблюдаемого потока в виде линейной функции  от k измеренных величин :

                                           (2)

Применение системы компьютерной алгебры эффективно в задачах большой размерности, т.к. делает возможным представление решения системы уравнений (1) в форме (2).

В качестве иллюстрации изложенного подхода рассмотрим систему с разделением и слиянием потоков, представленную на рис 1. Пусть на вход поступает поток с расходом , на выходе - . В данном случае число переменных n=9 и количество узлов m= 5.

Определим минимальное количество средств измерений в схеме потоков, приведенной на рис. 1. Система балансовых уравнений (1) для расхода   имеет вид

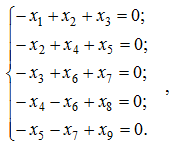                                 (3)

матрица коэффициентов системы уравнений (3)

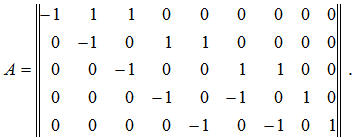                     (4)

Поскольку для матрицы (4) , число независимых параметров равно k=4, а остальные можно вычислить. Таким образом, достаточно использовать 4  прибора, но их произвольное расположение в поточной схеме может привести к ненаблюдаемым потокам. Так, если измеряются расходы на входе и выходе системы  то мы получим ненаблюдаемые значения внутри системы  (рис.1) и такое расположение неприемлемо.

Применим символьные вычисления для размещения наименьшего количества средств измерения, позволяющих вычислить расход всех потоков на приведенной схеме. Для решения использован программный пакет системы компьютерной алгебры Maple. Общее решение системы в символьном виде записывается следующим образом:

          (5)

где  - транспонированная матрица.

Пусть измеряются 4 параметра  (рис.1). Как следует из решения (5), остальные переменные представляют линейную комбинацию измеренных величин:

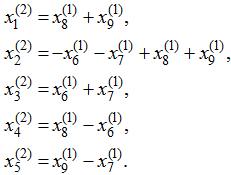
Если один из выбранных приборов  не работает, то нельзя определить состояние системы. Рассмотрим задачу о дополнительных приборах, которые обеспечат измерения даже в случае неисправности одного из измерительных устройств.

Используем следующий эвристический алгоритм выбора оптимального количества и места установки таких приборов. Во-первых, решение задачи (1) представим в символьном виде; во-вторых, выберем переменную, которая представляет линейную комбинацию максимального количества измеряемых величин. Оптимизация предполагает минимальное количество приборов, при этом множество ненаблюдаемых переменных – пустое.

Рассмотрим применение данного подхода на примере (3), с поточной схемой, представленной на рис.1. Анализ решения (2) показывает, что для повышения надежности следует дополнительно установить прибор для измерения расхода потока , поскольку в общем решении системы (5) значение  представляет  линейную комбинацию всех остальных измерений.

Решение в данном случае размещения приборов единственно, и, как следует из формулы (2), является оптимальным. Практически это означает, что при поломке одного из приборов все переменные в данном случае вычисляются и являются наблюдаемыми.

На практике приходится иметь дело с ситуацией, когда средства измерения уже используются в технологическом процессе. В этом случае при постановке задачи рекомендуется рассматривать эти переменные как измеряемые и вычислять оставшееся количество приборов, достаточное для автоматизации сведения баланса при уже существующей конфигурации измеряемых потоков.

Разработанные алгоритмы использовались при построении системы согласования материального баланса нефтеперерабатывающего завода с числом потоков более тысячи. Определялось минимальное количество измерительных средств и их размещение. Были проведены поэтапные исследования, начиная с отдельных групп технологических установок, до всего производства в целом. На основе полученных результатов принимались управленческие решения по установке недостающих средств измерения.

При проектировании новых технологических установок алгоритм использовался для вычисления оптимального расположении приборов с целью учета движения нефти и нефтепродуктов и управления производственными процессами. Изложенные выше подходы дали возможность избежать излишних эксплуатационных расходов на обслуживание приборов без ухудшения качества согласования баланса.

Таким образом, использование разработанной методики позволяет рассчитать минимальное количество приборов в балансовых системах учета и указать их оптимальное размещение. Предложенный в работе подход может быть успешно использован при создании и модернизации автоматизированных систем учета и управления материальными потоками.

Список литературы / References

1. Birchal1 V. S., Passos M. L. Modeling And Simulation Of Milk Emulsion Drying In Spray Dryers // Brazilian Journal of Chemical Engineering. – 2005. – V. 22. – N. 02. – P. 293 - 302.
2. Jurendić T. Applicability of Simple Mass and Energy Balances in Food Drum Drying // J. Basic. Appl. Sci. Res. – 2014. – N. 4(1) – P.128-133.
3. Narasimhan S., Jordache C. Data reconciliation and gross error detection. – Houston: Golf Publishing Company, 2000. – 406 p.
4. Кувыкин В.И. Использование моделей бизнес-процессов НПЗ в системах планирования и учёта // Мир нефтепродуктов. Вестник нефтяных компаний. – 2013. – № 7. – С. 47-48.
5. Кувыкин В.И., Мелешкевич М.А., Наумова С.В. Системный подход к оптимизации управления смешением // Международный научно-исследовательский журнал. – 2016. – № 10-2 (52). – С. 133-136.
6. Кувыкин В.И. Проводящий цилиндр в осесимметричном магнитном поле // Проблемы машиностроения и надежности машин. – 1998. – №2. – С.123-129.
7. Кирсанов М.Н. Графы в Maple. – М.: Изд-во ФИЗМАТЛИТ, 2007. – 168 с.
8. Кувыкин В.И., Кувыкина Е.В. Согласование данных и диагностика неисправности приборов в системах измерения// Прикладная механика и технологии машиностроения. – 2009. – № 2. – С.55 – 61.
9. Korn G. A., Korn T. M. Mathematical Handbook for Scientists and Engineers. – New York: McGraw-Hill Book Company, 1968. – 1130 p.

Список литературы на английском языке / References in English

1. Birchal1 V. S., Passos M. L. Modeling And Simulation Of Milk Emulsion Drying In Spray Dryers // Brazilian Journal of Chemical Engineering. – 2005. – V. 22. – N. 02. – P. 293 - 302.
2. Jurendić T. Applicability of Simple Mass and Energy Balances in Food Drum Drying // J. Basic. Appl. Sci. Res. – 2014. – N. 4(1) – P.128-133.
3. Narasimhan S., Jordache C. Data reconciliation and gross error detection. – Houston: Golf Publishing Company, 2000. – 406 p.
4. Kuvykin V.I. Ispol'zovanie modelej biznes-processov NPZ v sistemah planirovanija i uchjota [Refinery busyness process models application in plan and accounting systems]. // Mir nefteproduktov. Vestnik neftjanyh kompanij [World of Oil Products. The Oil Companies’ Bulletin]. – 2013. – № 7. – P. 47-48. [in Russian]
5. Kuvykin V.I., Meleshkevich M.A., Naumova S.V. Sistemnyj podhod k optimizacii upravlenija smesheniem [Systems-based approach to optimizing the blending management] // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. [International research journal]. – 2016. – № 10-2 (52). – P. 133-136. [in Russian]
6. Kuvykin V.I. Provodjashhij cilindr v osesimmetrichnom magnitnom pole [Conductive cylinder in an axially symmetric magnetic field] // Problemy Mashinostraeniya i Nadezhnos'ti Mashin [ Journal of Machinery Manufacture and Reliability] 1998. №2. P. 123-129. [in Russian]
7. Kirsanov M.N. Grafy v Maple. [Graphs in Maple]. M.: Izd-vo FIZMATLIT, 2007. 168 p. [in Russian]
8. Kuvykin V.I., Kuvykina E.V. Soglasovanie dannyh i diagnostika neispravnosti priborov v sistemah izmerenija [Data reconciliation and faults diagnosis of devices in measurement systems] // Prikladnaja mehanika i tehnologii mashinostroenija [Applied mechanics and mechanical engineering]. – 2009. – № 2. – P.55 – 61. [in Russian]
9. Korn G. A., Korn T. M. Mathematical Handbook for Scientists and Engineers. – New York: McGraw-Hill Book Company, 1968. – 1130 p.