ВЛИЯНИЕ ОБЪЕМА ВЫБОРКИ ДАННЫХ ЭНЕРГОПОТРЕБЛЕНИЯ НА ОШИБКУ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Бедерак Я. С.¹,  Лутчин Т. Н.², Кудрицкий М. Ю.³

²Аспирант, ³магистрант,  Институт энергосбережения и энергоменеджмента, Национальный технический университет Украины «Киевский политехнической институт», г. Киев, ¹ инженер, ПАО «АЗОТ»,  г. Черкассы

ВЛИЯНИЕ ОБЪЕМА ВЫБОРКИ  ДАННЫХ ЭНЕРГОПОТРЕБЛЕНИЯ НА ОШИБКУ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Аннотация

В представленной статье наведены результаты исследований влияния объема выборок данных энергопотребления на ошибку вычисления математической модели, которая вычисляется для ее описания. При анализе выборок учетных данных разного объема были определены методы максимально точного восстановления утерянных значений с обоснованием условий их применения.

Ключевые слова: парный коэффициент корреляции, выбор математической модели, энергопотребление.

Bederak Yа.S.¹, Lutchуn T.M.², Kudritskiу M.Yu.³

²PhD st., ³undergraduate, Institute for Energy Saving and Energy Management, National Technical University of Ukraine "Kiev Polytechnic Institute", Kiev, ¹engineer, PJSC "AZOT", Cherkassy

EFFECT OF THE SAMPLE SIZE OF  ENERGY CONSUMPTION DATA FOR ERRORS MATHEMATICAL MODEL

Abstract

In this paper the results of the effect by the volume of data samples of energy consumption for calculation error of the mathematical model are presented for its depicting. Analyzing samples of accounting data of different volume were determined as accurately as possible with the usage of  recovering methods for the lost values with their substantiation.

Keywords: pair correlation coefficient, choice of the mathematical model, energy consumption.

Согласно ПУЭ все предприятия должны быть оборудованы приборами учета электроэнергии. Учетные данные электропотребления могут быть утеряны вследствие ошибок персонала, сбоя оборудования, повреждения линий связи или программного обеспечения. Актуальность указанной проблемы была представлена ранее авторами в работе [1].  Утерянные данные рациональнее и проще всего восстанавливать регрессионным методом восстановления [2], но для этого необходимо знать оптимальный объем выборки данных, при котором их восстановление будет наиболее точным.

С одной стороны, чем больше объем выборки, тем лучше учтены будут в математической модели особенности ведения технологического процесса. А с другой стороны, чем меньше объем выборки, то тем меньше влияние сезонных составляющих, изменения температуры окружающей среды.

Пропуски как зависимых, так и независимых переменных ставят задачу определения определенного вида математической модели, которую можно использовать для восстановления данных. Для однофакторной модели y = f (x) это может достигаться путем построения моделей вида  y = f (x) и x = f (y) с помощью парной регрессии.

Для двухфакторной зависимостей при парном коэффициенте корреляции между зависимой и независимыми переменными более 0,75 целесообразно строить три однофакторные модели при помощи парной регрессии вместо множественной регрессии. Это проще и более эффективно, чем построение множественной линейной регрессии и не требует специального программного обеспечения, как у метода группового учета аргументов [3].

Модели строятся по различным объемам начальных выборок. Выбирается модель, которая имеет оптимальное соотношение ошибок моделей для трех зависимостей.  Способ выбора лучшей математической модели описан в     работе [1].

Для доказательства того, что выборка объемом n при общем количестве N значений достаточна для качественного восстановления данных, необходимо проверить это путем расчета ошибки моделей нескольких выборок того же объема. Количество выборок объемом n зависит от отношения N / n и определяется по формуле Стерджесса (Штюргеса) [4]. Номера выборок получают с помощью генератора случайных чисел.

Для примера рассмотрим потребление и производство на промышленном заводе, а именно по производству аммиака. Так, если электропотребление Е  цеха зависит от объема выпуска аммиака А и от потребления природного газа  Г, то при наличии пропусков данных и в зависимых, и в независимых переменных и при тесной связи между этими переменными необходимо для восстановления данных строить 3 модели: Е = f (A), A= f (G), G = f (E).

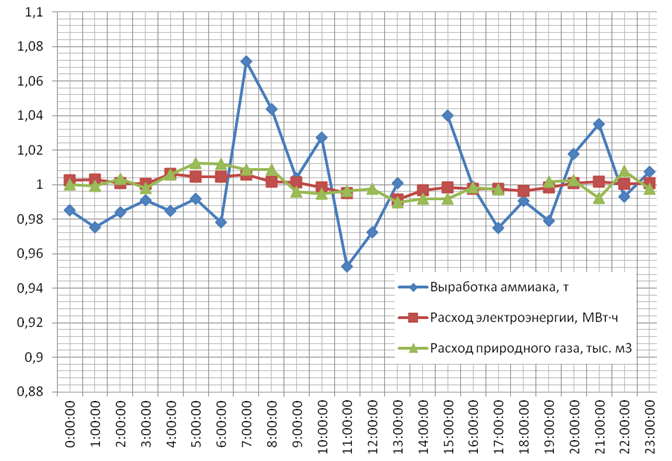
Фрагмент исходных данных приведен на рис. 1. Пробелы данных показаны разрывами графика. Исходные значения выработки аммиака А = 40,29 т, расхода электроэнергии  E  = 31,91 МВт·ч, расхода природного газа G = 45,21 тыс. м³.

Рис. 1 – Исходные значения выработки аммиака, расхода электроэнергии  и  природного газа

Напомним, что для качественного восстановления данных необходимо перед использованием их проверить их на грубые ошибки критерием Ирвина [5]. Ошибки математических моделей рассчитывались в программном комплексе Matlab 7.0 (пакет Curve Fitting Tools) [6]. Исследовались выборки с комплектными рядками длительностью 24, 48, 168, 350, 700, 1050 часов. Методом перебора определялась средняя абсолютная процентная ошибка моделей MAPE [7] среди функций экспоненциальных Exp, Фурье Fourier, полиномиальных Polynom, степенных Power, рациональных RAT, синусоидальных SumSin, математическое описание которых было представлено ранее в работе [7].

Наилучшая модель выбирается из более, чем 50 моделей. Расчет занимает для каждого объема выборки около 3 часов. Поэтому, необходимо выбрать вид функции, обеспечивающей наилучшее качество восстановления данных, и использовать не все функции, а только 8÷10 шт.  Результаты расчетов представлены в табл. 1.

Таблица 1 - Результаты расчета ошибки моделей математических моделей зависимостей Е = f (A), A = f (G), G = f (E)

Способом, предложенным в работе [1], найдены математические методы, обеспечивающие оптимальное соотношение ошибок моделей для каждого объема выборки для трех зависимостей.

В полярных координатах круговая диаграмма разбивается на три сектора, которые содержат столько лучей, сколько математических моделей применяется (все вышеперечисленные в табл. 1). В масштабе отмечаются значения MAPE  на каждом луче. Вершины векторов на лучах соединяются в треугольники. Треугольник с минимальной площадью определяет оптимальную модель. Результаты расчета площади треугольников по каждой зависимости приведены в табл. 2.

Таблица 2 - Результаты расчета метода с минимальной ошибкой модели для каждого объема выборки трех зависимостей между разными потребленными ресурсами и выпущенной продукцией, ед. кв.

Вид математической модели	Объем выборки, ч
	24	48	168	350	700	1050
Exp	0,716	8,144	3,297	3,582	4,792	4,463
Fourier	0,637	34,728	2,697	29,111	4,135	3,565
Polynomial	1,179	9,165	2,917	3,602	4,007	3,618
Power	0,737	11,055	3,882	4,216	5,097	4,437
RAT	0,630	6,235	2,596	3,047	4,084	3,543
SumSin	1,176	3,689	1,650	2,765	3,704	3,215
Минимальное значение	0,630	3,689	1,650	2,765	3,704	3,215

Значение вида математической модели в табл. 3 и далее, при котором наблюдается оптимальное сочетание ошибок модели, выделено полужирным шрифтом.

 Наилучший метод восстановления данных для выборок объемом 48 часов и более – метод суммы синусоидальных функций. А для выборки объемом 24 часа – лучший метод – соотношения полиномов. Но если для анализа применяются выборки с разным объемом данных, то учитывая меру соизмеримости погрешности при помощи суммы синусоидальных функций, с целью унифицирования расчетов можно применять указанный метод во всех случаях.

Рассмотрим более детально вариант, когда выборки данных сформированы по часовым суточным значениях. Согласно представленной таблице проанализируем правильность выбора математической модели с наименьшей ошибкой. Это утверждение проверено при помощи генератора случайных чисел. В качестве репрезентативных согласно теории случайного распределения им из 45 суточных значений выбрано 6 суток под номерами   1, 5, 17, 32, 37, 39. Для массивов  суточных значений определена ошибка модели (табл. 3).

Таблица 3 - Результаты расчета метода с минимальной ошибкой модели для различных суточных объемов выборки для зависимостей E = f (A), A = f (G), G = f (E), кв. ед.

Вид математической модели	Номер суток
	№1	№5	№17	№32	№37	№39
Exp	0,716	0,365	0,164	0,446	0,158	0,196
Fourier	0,637	0,425	0,161	0,401	0,148	0,192
Polynomial	1,179	0,370	0,156	0,472	0,155	0,214
Power	0,737	0,357	0,163	0,451	0,156	0,225
RAT	0,630	0,324	0,157	0,397	0,143	0,208
SumSin	1,176	2,834	0,162	0,436	0,144	1,319
Минимальное значение ошибки	0,630	0,324	0,157	0,397	0,143	0,192

Таким образом, для всех суточных массивов целесообразно использовать отношение полиномиальных функций. Доказано, что для восстановления данных электропотребления в цехе аммиака достаточно использовать суточную выборку значений среднечасового расхода электроэнергии, газа и объема выпуска аммиака.

Рассчитывался парный коэффициент корреляции и определялась зависимость среднего значения ошибки модели от парного коэффициента корреляции  зависимостей Е  = f (A), A = f (Г), Г = f (Е) и от объема выборки. Результаты расчетов представлены в табл. 4.

Таблица 4 - Среднее значение ошибки модели (MAPE) и парный коэффициент корреляции (ПКК) для трех зависимостей между разными потребленными ресурсами и выпущенной продукцией с учетом объема выборки

Объем выборки	MAPE для А= f (Г), %	ПКК	MAPE для Е = f (А), %	ПКК	MAPE для Г= f (Е), %	ПКК
24	2,223	-0,088	0,271	0,190	0,546	0,716
48	4,605	0,762	1,457	0,890	3,117	0,787
168	2,401	0,886	0,867	0,947	1,343	0,923
350	7,059	0,871	1,186	0,786	1,337	0,790
700	2,180	0,924	1,528	0,802	1,775	0,789
1050	2,063	0,910	1,360	0,813	1,759	0,778

Из табл. 4 следует, что парный коэффициент корреляции не влияет на ошибку математической модели.

Выводы

В результате исследований были сделаны следующие выводы:

1. Предложен способ определения оптимального объема выборки данных, при котором восстановление их будет наиболее точным.
2. Для сокращения времени выбора оптимальной математической модели необходимо выбрать такой вид функции, который обеспечивал бы наилучшее качество восстановления данных.
3. Среднее значение ошибки модели не зависит от парного коэффициента корреляции однофакторных зависимостей между разными потребленными ресурсами и выпущенной продукцией.