УПРУГИЕ И ПЛАСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОРОШКОВЫХ МАТЕРИАЛОВ ПОСЛЕ СВОБОДНОЙ ОСАДКИ
Егорова Р.В.1, Егоров М.С.2
1Старший преподаватель кафедры «Информационные технологии»; 2Доцент, к.т.н. кафедры «Технический сервис» филиал ДГТУ в г. Волгодонске, aquavdonsk@mail.ru
УПРУГИЕ И ПЛАСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОРОШКОВЫХ МАТЕРИАЛОВ ПОСЛЕ СВОБОДНОЙ ОСАДКИ
Аннотация
Проблема неразрушающего контроля конструкционных материалов по фактическому состоянию является весьма актуальной, поскольку дефекты и изменения структуры материала, возникающие при изготовлении и в процессе эксплуатации изделий могут существенно уменьшить их прочность. Механические свойства материала несут ценную информацию для определения остаточного ресурса детали. Модули упругости − важнейшие характеристики твердого тела. Они являются расчетными параметрами в аналитическом аппарате физической теории деформации и разрушения твердого тела, входят во все основополагающие уравнения механики.
Ключевые слова: порошковые материалы, свободная осадка.
Egorova R.V.1, Egorov M.S.2
1Senior lecturer of chair «Information technologies»; 2Associate Professor, Ph.D. of the Department «Technical service» branch DGTU, in Volgodonsk, aquavdonsk@mail.ru
ELASTIC AND PLASTIC CHARACTERISTICS OF POWDER MATERIALS AFTER FREE SLUDGE
Abstract
The problem of nondestructive testing of structural materials on the actual state is highly relevant, as defects and changes in the structure of the material arising when manufacturing and maintenance process can significantly reduce their strength. Mechanical properties of the material are valuable information for the determination of residual resource of details. Moduli of elasticity of - the essential characteristics of a solid body. They are design parameters in the analytical apparatus of physical theory of deformation and fracture of rigid body, are all fundamental equations of mechanics.
Keywords: powder materials, free of sludge.
Значения модулей упругости и коэффициента Пуассона даже чистых веществ − элементов и химических соединений постоянного состава, определенные на материалах разной степени чистоты различными методами, − весьма различны, что свидетельствует об их недостаточной достоверности. В большей степени это относится к спеченным порошковым материалам, свойства которых существенно зависят от морфологии порового пространства.
Следует отметить, что сведений об изменении упругих характеристик спеченных материалов в зависимости от их пористости в отечественной и зарубежной литературе крайне мало. Часть из них посвящена теоретическим методам определения модулей упругости и коэффициента Пуассона [1], а часть− экспериментальным [2,3].
Одним из наиболее распространенных методов определения упругих характеристик материалов является ультразвуковой метод диагностики структуры и состояния материала. Он основан на анализе характеристик ультразвуковых волн, распространяющихся в объекте контроля. Для исследования неоднородностей и дефектов структуры материалов применяют методы ультразвуковой спектроскопии и дефектоскопии, основанные на анализе частотных зависимостей коэффициента затухания и фазовой скорости акустических волн в исследуемом материале [4]. По измерениям фазовых скоростей акустических волн в широком частотном диапазоне проводится расчет упругих модулей твердых тел, в частности анизотропных композиционных материалов [5].
Для исследования упругих характеристик образцов были выбраны два материала шведской фирмы «Hoganas» : Astaloy 0,85 Mo и NC 100.24.
Ультразвуковые исследования порошковых сталей проводились в два этапа. Измерения проводились при комнатной температуре в диапазоне частот 0,2 – 50 МГц. На исследуемых образцах первоначально измеряли скорость звука в продольном направлении 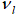 универсальным толщинометром Krautkramer DMS2, а на следующем этапе производили замеры скорости звука в поперечном направлении
универсальным толщинометром Krautkramer DMS2, а на следующем этапе производили замеры скорости звука в поперечном направлении 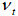 дефектоскопом Krautkramer USM 25. В качестве контактной смазки использовался глицерин. Результаты измерений скоростей
дефектоскопом Krautkramer USM 25. В качестве контактной смазки использовался глицерин. Результаты измерений скоростей 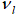 и
и 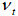 в исследуемых образцах занесены в табл. 2 используя значения табл.1
в исследуемых образцах занесены в табл. 2 используя значения табл.1
Таблица 1
| Начальная пористость П0,% | Удельная работа деформаци | Исходный материал | Плотность после осадки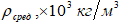 |
Толщина после осадки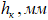 |
| и W, МДж/м3 | ||||
| 30 | 70 | Astaloy 0,85 Mo | 6,16 | 8 |
| 20 | 80 | 6,99 | 7,5 | |
| 10 | 135 | 7,3 | 5,6 | |
| 30 | 72 | NC 100.24 | 6,17 | 8 |
| 20 | 75 | 6,93 | 7,7 | |
| 10 | 130 | 7,3 | 5,9 |
Методика определение значений 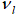 и
и 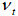 рассмотрена в работах [5,6] и определяется по формулам
рассмотрена в работах [5,6] и определяется по формулам 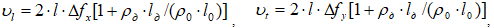
где 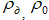 - плотность кварцевого датчика и образца;
- плотность кварцевого датчика и образца; 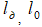 - длины кварцевого датчика и образца;
- длины кварцевого датчика и образца; 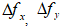 - средние разности частот между соседними гармониками. Модули упругости определялись по соотношениям [7]
- средние разности частот между соседними гармониками. Модули упругости определялись по соотношениям [7]
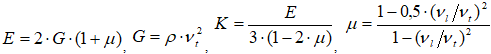 (1)
(1)
Максимальная относительная погрешность определения модуля Юнга в применяемом оптико-акустическом методе составляет 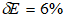 , модуля сдвига -
, модуля сдвига - 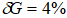 , коэффициента Пуассона -
, коэффициента Пуассона - 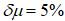 .
.
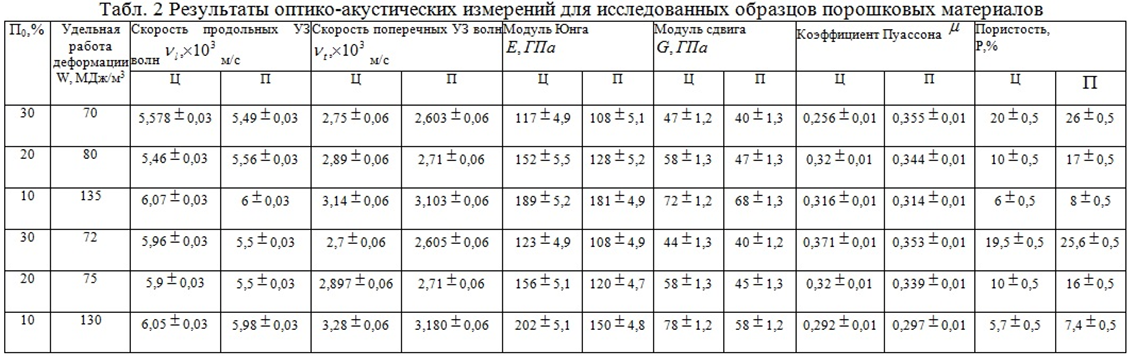
Результаты измерений фазовых скоростей продольных и сдвиговых ультразвуковых волн, а также рассчитанные по формулам (1) значения модулей Юнга, сдвига и коэффициента Пуассона, а также значения пористости в центре (Ц) и на периферии (П) всех исследованных образцов представлены в табл.2. Определение объемной пористости P по теоретически расчетным и экспериментально измеренным значениям скоростей продольных ультразвуковых волн [1,7] в исследованных участках образцов дает величины представленные в табл.2.
Распределение и скорость распространения ультразвуковых волн тем выше, чем плотнее исследуемый материал в центральной зоне и, разуплотнение, наблюдаемое на периферии, обуславливает меньшие скорости ультразвуковых волн, что указывает на большое количество микро- и макродефектов образованных канальными соединениями пор в местах деформационного течения материала. Однако, одинаковые значения продольных скоростей в центре и на периферии, а также незначительно большие значения продольных скоростей на периферии относительно центра свидетельствуют о нелинейном распределении деформируемого материала в объеме исследуемого образца.
Таким образом, экспериментально реализованный ультразвуковой метод измерения локальных упругих модулей образцов изотропных твердых тел позволяет проводить неразрушающие измерения упругих модулей в образцах толщиной 0,1 – 70 мм с локальностью в поперечном направлении 1 – 2 мм. При этом максимальная относительная погрешность определения модуля Юнга в применяемом оптико-акустическом методе составляет 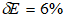 , модуля сдвига -
, модуля сдвига - 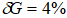 , коэффициента Пуассона -
, коэффициента Пуассона - 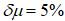 даже для сильно поглощающих ультразвук образцов (коэффициент затухания продольных акустических волн может достигать десятков обратных сантиметров).
даже для сильно поглощающих ультразвук образцов (коэффициент затухания продольных акустических волн может достигать десятков обратных сантиметров).
Как показали результаты, ультразвуковой метод дает возможность измерения локальных значений упругих модулей неоднородных твердых тел, в случаях, когда классические методы контроля трудно выполнимы, так как изготовление образцов сложной фигурной формы с высокой пористостью затруднительно.
Анализ полученных результатов позволяет сделать вывод о том, что полученные значения модулей упругости подтверждают неравномерное распределение плотности композиционных материалов. Сопоставив значения модулей упругости центральной и периферийной зон исследуемых образцов, следует отметить нелинейный характер распределения деформируемого материала в объеме исследуемого образца.
Список литературы
Григорьев А.К., Рудской А.И. Деформация и уплотнение порошковых материалов. М.:Металлургия, 1992.192с.
А.А.Карабутов, Л.И.Кобелева, Н.Б. Подымова, Т.А. Чернышова Измерение упругих модулей композиционных материалов, упрочненными частицами, лазерным оптико-окустическим методом./ Заводская лаборатория. Диагностика материалов. №3. 2009. Т.75. – С. 27 – 33.
Акимов В.В., Иванов Н.А. Применение ультразвукового резонансного метода для определения упругих и пластических характеристик сплавов TiC – TiNi / Прикладная механика и техническая физика. 2002. Т. 43. №2. С. 203 – 207.
Layman C., Murhy N.S., Yang R.-B., Wu J. The interaction of ultrasound with particulate composites / J. Acoust. Am. 2006. V. 119. №3. P. 1449 – 1456.
Кретов Е.Ф. Ультразвуковая дефектоскопия в энергомашиностроении /СПб: Издательство СВЕН 2007. – 296 с.
Баулин С.С., Нуцер М.Л., Фридман Г.Р. Неразрушающий контроль изделий из порошковых материалов с помощью ультразвуковых колебаний// Кузнечн.- штамп. Пр-во.1981. №1.С. 157-163.
Поляков В.В., Головин В.А. Влияние пористости на скорость ультразвуковых волн в металлах / Письма в ЖТФ. 1994. Т. 20. №11. С.54 – 57.